新高考背景下高考数学卷与学业质量标准的一致性研究

吴佳敏 林子植 石天然

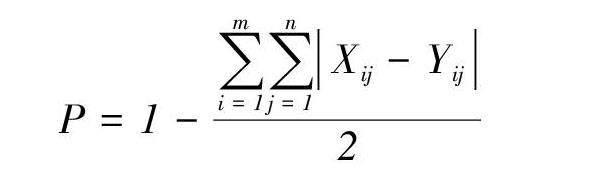
摘   要：在新高考和新课标的背景下，高考试题是衡量教育改革的重要性指标。采用SEC一致性模型，构建内容主题和学业质量水平的分析框架，从学业质量标准的内容主题、表现水平和核心素养三个维度对首批新高考改革试点上海和浙江的14套高考数学卷进行研究。基于研究结果，对提升试卷与学业质量标准的契合程度给出建议：量化学业质量标准，使教评有章可循；调整内容主题比例，实现评标一体化；把控认知表现水平，完善学业评价体系；均衡核心素养分布，令命题合理科学；研制本土一致性评价工具，贴合我国国情。

关键词：新高考；新课标；学业质量标准；高考数学卷；一致性

在新高考和新课标的背景下，高考试题作为衡量教育改革的重要指标。上海、浙江是最早开始进行高考综合改革的试点省市，研究两个城市高考数学卷与学业质量标准的一致性，对其改革成果进行检验反馈与经验总结，能够为后续推进高考综合改革提供一定的参考依据。鉴于此，本文以2017—2023年上海和浙江两地高考数学试卷为研究样本，分析基于新高考数学评价机制和数学学业质量标准的适切性，以期为高考数学命题者提供相关数据和为教师教学提供一定参考。

一、研究设计

1.研究对象

选取《普通高中数学课程标准（2017年版2020年修订）》（以下简称《标准》）中的“学业质量标准”和上海、浙江14套新高考数学试卷作为研究对象，分别为2017—2023年上海高考数学试卷（以下简称“上海卷”）7套和2017—2023年浙江高考数学试卷（以下简称“浙江卷”）7套。

2.研究工具

美国学者诺曼·韦伯（Norman Webb）研发了评价与课程标准的一致性研究工具，他认为一致性指的是事物之间相匹配的程度。1 在此基础上，美国学者安德鲁·波特（Andrew Porter）等人构建了SEC一致性分析模式，该模式通过引入一致性指数来衡量评价项目和课程标准的一致性。2 该工具通过简单明了的方式展示评价结果，并借助MATLAB软件中的函数运算得到具体的一致性指数和临界值。SEC一致性分析模式因其科学性和广泛性受到研究者的广泛认可。3 故本研究采取SEC一致性分析模式，其中主要涉及四个关键步骤：构建二维矩阵、编码和统计、标准化和计算一致性系数，以评估高考数学卷和认知水平之间的一致性程度，模型如下：

[P=1-i=1mj=1nXij-Yij2]

在该模型中，一致性系数P表示评价项目和课程标准之间的一致性程度。其中，m代表二维矩阵的行数，n代表二维矩阵的列数。[Xij]、[Yij]分别为《标准》中的学业质量标准和高考数学试卷对应的第[i]行、第[j]列的具体数值；P介于[0，1]之间，P与1越接近，意味一致性程度越高，反之亦然。

3.研究过程

（1）编码框架确定

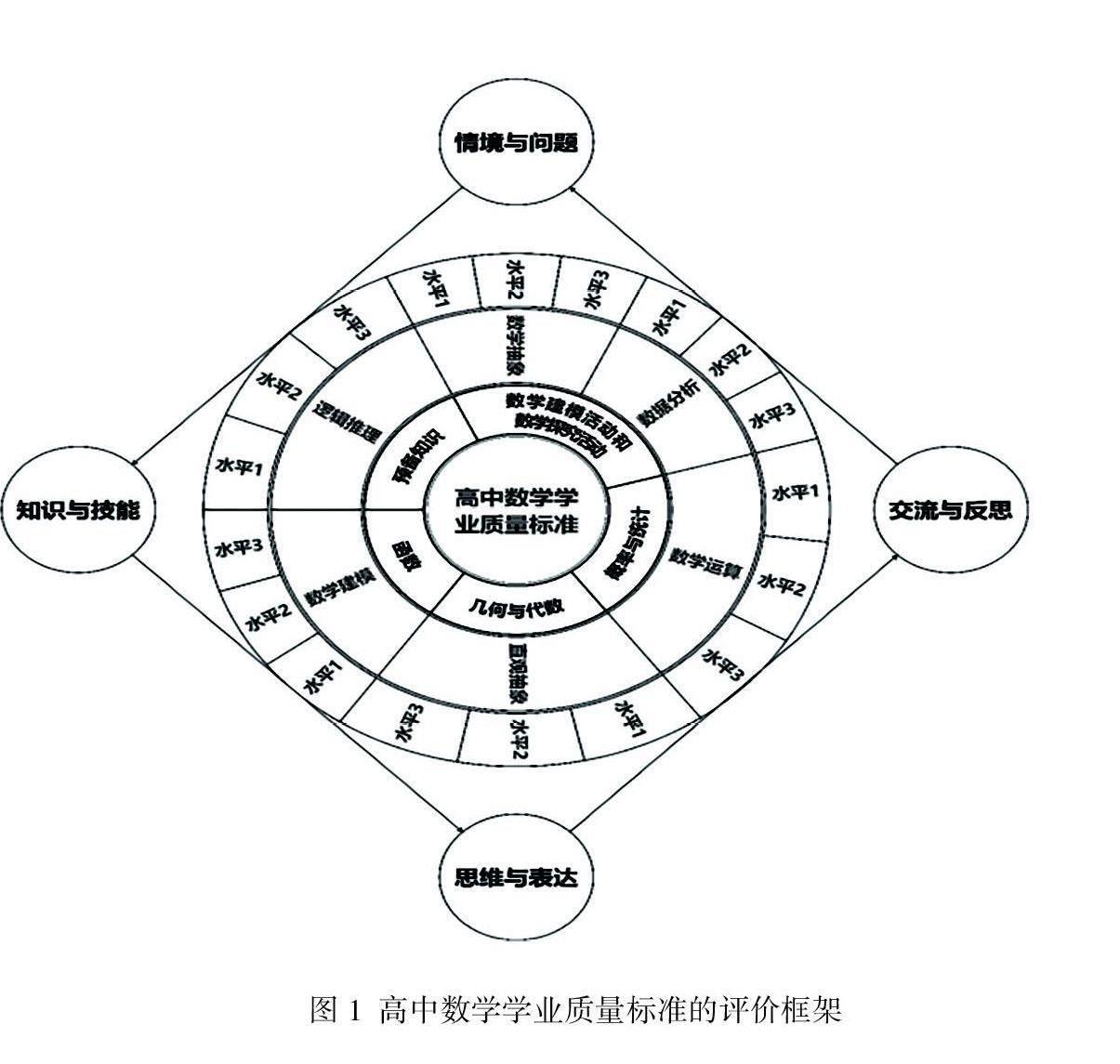
高中数学学业质量标准是以学科核心素养和表现水平为主要维度，结合课程内容来描述学生学业成就的表现4 ，为了更好地展示学业质量标准评价框架体系，根据《标准》中对此模块的具体描述，以此绘制其框架图（见图1）。5 由图1可知，知识点内容和试题涵盖核心素养的四个方面：情境与问题、知识与技能、思维与表达和交流与反思。在此基础上，将课程内容和数学核心素养及其表现水平作为主要维度，构建二维矩阵模式：

内容主题×学业质量水平（核心素养表现水平和核心素养类型）

在SEC一致性模型的二维矩阵中，“内容主题”对应评价框架中的课程内容，而核心素养及其表现水平合称为“学业质量水平”，对应二维矩阵中的“认知水平”。

①内容主题

根据《标准》，高中数学课程分为必修、选择性必修和选修三个部分。为了研究方便，选取必修和选择性必修两个板块进行研究。高中数学课程涵盖预备知识、函数、几何与代数、概率与统计、数学建模与探究这五个主题。其中，预备知识、函数、几何与代数、概率与统计是高考主要考查的内容，因此我们将内容主题划分为这四个维度。

②学业质量水平

根据学业质量标准，将学业质量划分为表现水平和核心素养两个维度。其中，表现水平分为3个级别，核心素养涵盖了6个方面，具体参考《标准》的学业质量标准对于核心素养三水平六方面的细化描述。

基于核心素养及其表现水平，将上述内容主题和学业质量水平进行结合，确定一致性分析框架。

（2）信效度分析

在进行内容编码和试卷编码前，首先对4位具有高中数学教学经验的研究者培训（其中两位是高中数学组骨干教师，另两位分别取得硕士和博士学位），明确相关编码准则和步骤。然后由他们对学业质量标准和高考数学卷进行编码，逐个判断其内容主题、表现水平和核心素养。每位编码者独立编码，对存在分歧的部分进行讨论与协商，并向权威专家咨询，最终确定编码结果，以此保证编码的客观性和准确性。据学者安德鲁·波特等人研究表明，当4位以上内容专家进行编码时，其所得结果的一致性信度达到了可接受的水平1 ，并借助SPSS对学业质量标准和高考数学卷进行信度分析，得到一致性系数分别为0.842和0.796，信度较高。

（3）对学业质量标准和高考数学卷编码

①对学业质量标准编码

对内容主题进行编码的过程如下：首先，将4个内容主题分别编码为1、2、3、4，分别代表预备知识、函数、几何与代数、概率与统计。然后，对每个内容主题下的二级主题进行编码。最后，对二级主题下的每个子目标逐条进行编码。

学业质量水平编码过程如下：将6个核心素养编码为A、R、M、I、O和D，分别代表数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。对每个核心素养下的3个水平进行编码，以数据分析为例，编码为D.1、D.2和D.3。对于含有多个知识点的三级主题进行拆分编码；对于含有不同认知水平的三级主题拆分编码，并采取平均分配原则。

通过上述内容主题和学业质量水平的编码方法对学业质量标准进行编码，共得到268条编码内容，便于后续计算和化简进行标准化处理，得到学业质量标准的比率表（见表1）。

②对高考数学卷编码

对上海卷和浙江卷进行编码的过程如下：首先，分析每道试题考查的知识点，并与《标准》相对应。然后，具体分析每题所涉及的表现水平，并确定相应的数学核心素养。根据参考答案判断每道题在内容主题、表现水平和核心素养下的分值，如果一道题涉及多个知识点、表现水平和核心素养，按照参考答案所占的分值进行折算。进而统计计算总分，并将其折合为总和为1的比率表。以2017年上海卷的编码结果为例（见表2），其余样本试卷均按照相同的方法进行标准化处理。

二、研究结果与分析

1.一致性系数

（1）一致性系数参考值[P0]

在对学业质量标准和高考数学卷的二维矩阵进行标准化处理后，需要确定一致性系数P的临界值[P0]。当P达到临界值[P0]时，表示达到统计学意义上的显著一致性。通过MATLAB软件计算[P0]值，借鉴了美国学者加文·富尔默（Gavin W. Fulmer）关于一致性的研究思路1，将学业质量标准的知识点内容要求总数和高考数学卷的总分进行随机赋值，形成所需的二维矩阵，重复2万次后得到2万个随机矩阵，在对随机矩阵进行标准化处理，得到14套数学卷的一致性系数参考值[P0]。

（2）高考数学卷和学业质量标准的一致性系数P

将学业质量标准和高考数学卷得到的编码数据统计表的数值代入Porter指数一致性公式， 通过MATLAB软件计算，得出了14套卷子的一致性系数P，并获得了一致性系数参考值[P0]（见表3）。

2.结果分析

（1）高考数学卷和学业质量标准的总体一致性分析

2017—2023年浙江省和上海市共14套试卷与学业质量标准的一致性系数在0.33—0.45之间浮动。其中有两套高考数学卷与学业质量标准（上海卷2022、浙江卷2023）的一致性系数大于参考值，说明这两套试卷与学业质量标准具有统计学意义上的一致性。其余12套试卷与学业质量标准的一致性均小于参考值，说明两者不具有统计学意义上的一致性。其中浙江卷2023一致性最高（0.4485），高出参考值0.0036，说明这套试卷与学业质量标准最符合。浙江卷2020一致性最低（0.3365），低于参考值0.1089，说明这份试卷与学业质量标准较不符合。

对比浙江省和上海市的一致性系数和参考值的差值可以发现，上海高考数学卷在参考值周围浮动，最大差值为0.0817，而浙江省高考数学卷的差值较大，最大差值达到0.1089。从同一省市的不同年份来看，上海卷前三年与学业质量标准的一致性符合程度处于波动状态，到2019年波动差值达到最大，后四年逐渐趋于稳定，尤其是2022年和2023年，差值明显减小。浙江卷整体波动比较大，前三年与学业质量标准一致性系数均低于参考值，到2020年差值达到峰值，后两年有下降趋势，但仍有大幅波动，在2023年与学业质量标准一致性系数吻合较好。

（2）高考数学卷和内容主题一致性分析

通过对学业质量标准和高考数学卷编码数据进行统计和梳理，学业质量标准的四个内容主题安排比重为：预备知识（11.9%），概率与统计（23.9%），几何与代数（30.6%），函数（33.6%）。从整体趋势来看，预备知识和概率与统计的考查均略低于学业质量标准的要求，函数和几何与代数的考查高于学业质量标准的要求，从7套上海卷和7套浙江卷在各个主题所占比重发现，上海卷在函数占比稍高，浙江卷在几何与代数所占权重更大。其中上海卷2017、上海卷2019、上海卷2022和浙江卷2018四套试卷与学业质量标准稍有差异，这可能和当年知识点考查偏重相关。

在预备知识主题上，上海卷2019（11.9%）与学业质量标准（11.9%）达到一致性，其余13套数学卷均低于学业质量标准要求。在函数主题上，上海卷2022（34.0%）和学业质量标准（33.6%）基本达到一致，其余13套数学卷均高于学业质量标准要求。在几何与代数主题上，浙江卷2022（30.3%）和学业质量标准（30.6%）大体达到一致，浙江卷2017（29.3%）略低于学业质量标准的要求，上海卷2019（32.7%）略高于学业质量标准要求，其余11套试卷均明显高于学业质量标准，其中上海卷2022（49.3%）最高，超出18.7%。在概率与统计主题上，14套高考数学卷均低于学业质量标准要求，其中上海卷2023（18.3%）在14套卷中与学业质量标准（23.9%）的差异最小，上海卷2017（4.4%）和浙江卷2018（2.6%）与学业质量标准差异较大，这可能和新高考改革有关，导致前两年处于不稳定的状态。

（3）高考数学卷和表现水平一致性分析

通过对学业质量标准和高考数学卷编码数据进行统计和梳理，学业质量标准的表现水平在各水平所占比重为：水平2（48.5%）>水平1（34.3%）>水平3（17.2%）。从整体上来看，上海卷2017和上海卷2023比较符合表现水平分布，在14套高考卷中，上海卷2021分布是水平1（60.6%）>水平3（24.0%）>水平2（15.4%），而其余11套高考数学卷分布均是：水平1>水平2>水平3。对水平1而言，上海卷2017（33.5%）和表现水平（34.3%）一致性程度最高，其余各套卷和表现水平的差值在-0.091—-0.305之间浮动，其中浙江卷2022、上海卷2021和浙江卷2020与表现水平的差异性较大，差值分别为：-30.5%、-26.3%和-25.8%。从水平2来看，上海卷2023（47.2%）和表现水平（48.5%）最为切合，其余各套卷与表现水平的差值在0.092—0.331上下波动，上海卷2021和浙江卷2022与表现水平的差异性较大，差值分别为：33.1%和30.7%。从水平3来看，14套高考数学卷和表现水平的差值在0.086—0.114之间浮动，在三个水平间与表现水平的差异最小，其中浙江卷2022（17.4%）与水平3（17.2%）最为一致。浙江卷2017和浙江卷2019相比其余各数学卷来看，差值较大，分别为8.6%和8.5%，可以看出前三年仍是处于不稳定的状态。从两个省份来看，对于水平1和水平3的考查，上海卷与学业质量标准的表现水平更为契合，而对水平2的考查，浙江卷和学业质量标准的表现水平更为一致。

（4）高考数学卷和核心素养一致性分析

通过对学业质量标准和高考数学卷编码数据进行统计和梳理，学业质量标准对数学核心素养的要求较为均衡，对于A（28.1%）要求最高，I（17.9%）、O（17.5%）、M（15.2%）素养的要求占比相差不大，R（11.2%）和D（10.1%）素养要求较低。从整体来看，上海卷在核心素养的分布大体是：O>R>A>I，其中D和M素养相差不大，考查相对较低；浙江卷在核心素养的大致分布为：O>R>I>A，对于D和M素养的考查也相对较低。从数学抽象素养来看，14套高考数学卷均略低于学业质量标准的要求，差值在0.045—0.221浮动，其中上海卷2021（23.6%）与学业质量标准（28.1%）最为接近，浙江卷2018（6.0%）、浙江卷2017（6.1%）和浙江卷2021（7.0%）与学业质量标准的差异性较大。从逻辑推理素养来看，14套高考数学卷均略高于学业质量标准的要求，差值在-0.056—-0.223波动，浙江卷2020（33.5%）、浙江卷2021（32.6%）和上海卷2019（28.4%）显著高于学业质量标准的要求。从数学建模素养来看，学业质量标准的要求略高于14套高考数学卷，差值在0.08—0.152之间浮动，其中上海卷2019未考查数学建模素养，浙江卷2022（1.0%）、上海卷2022（1.1%）、浙江卷2020（1.2%）均考查较低。从直观想象素养来看，学业质量标准的要求略高于14套高考数学卷，差值在0.015—0.099之间浮动，其中浙江卷2017（16.4%）和学业质量标准（17.9%）最为接近。从数学运算素养来看，14套高考数学卷明显高于学业质量标准的要求，差值在-0.16—-0.357之间，浙江卷2018（53.2%）、浙江卷2019（49.5%）、浙江卷2017（48.9%）与学业质量标准要求的一致性存在一定差距，说明浙江省前三年对于考查何种核心素养为重心也处于探索阶段。从数据分析素养来看，浙江卷2023（16.1%）高于学业质量标准（10.1%），其余13高考数学卷均低于学业质量标准要求，差值在0.016—0.101之间浮动，其中浙江卷2017、浙江卷2019和上海卷2021均未考查数据分析素养。

三、结论与建议

1.研究结论

（1）总体上，14套高考数学卷中2套和学业质量标准具有统计学意义上的一致性

上海卷2022和浙江卷2023与学业质量标准具有统计学意义上的一致性，浙江卷2023与学业质量标准的一致性最高（0.4485），高出参考值0.0036，说明这套试卷与学业质量标准最符合，进一步说明了高考数学卷和学业质量标准之间的一致性程度也在逐年递升。而浙江卷2020与学业质量标准的一致性最低（0.3365），低于参考值0.1089，说明这份试卷与学业质量标准较不符合。从浙江省和上海市的一致性系数和参考值的差值上可以发现，由于2017年是高考改革第一年，在前三四年两个省份高考数学卷中其P和[P0]的差值一直处于波动状态，后两年逐渐趋于稳定，和学业质量标准的一致性也逐渐提高。

（2）在内容主题分布上，14套高考数学卷中4套与学业质量标准具有差异

在内容主题分布上，上海卷2017、上海卷2019、上海卷2022和浙江卷2018四套试卷与学业质量标准存在不一致，其余10套高考数学卷大体上比重排序依次为预备知识、概率与统计、几何与代数和函数；各个内容主题的安排比重是一致的，在预备知识和概率与统计的考查均略低于学业质量标准的要求，函数和几何与代数高于学业质量标准的要求。上海卷和浙江卷在各个主题所占比重上，上海卷在函数上占比稍高，浙江卷在几何与代数上所占权重更大。在预备知识主题上，上海卷2019与学业质量标准达到一致；在函数主题上，上海卷2022和学业质量标准基本达到一致；在几何与代数主题上，浙江卷2022和学业质量标准大体达到一致；在概率与统计主题上，14套试卷均低于学业质量标准要求，上海卷2023与学业质量标准的差异最小。

（3）在表现水平分配上，14套高考数学卷有2套与学业质量标准大同小异

高考数学卷与学业质量标准的表现水平上存在一定差异，学业质量水平从大到小排序是：水平2、水平1和水平3，在14套试卷中只有上海卷2017和上海卷2023符合学业质量标准的表现水平分布，而上海卷2021从大到小的排序是：水平1、水平3和水平2，剩余的11套试卷在各水平从大到小排序均是：水平1、水平2和水平3。从水平1的考查来看，上海卷2017和表现水平一致性程度最高；从水平2的考查来看，上海卷2023和表现水平最为切合；从水平3的考查来看，浙江卷2022与表现水平的最为一致。

（4）在核心素养考查上，14套高考数学卷与学业质量标准有所不同

学业质量标准对数学核心素养的要求较为均衡，从高到低的排序是：A、I、O、M、R和D；上海卷的分布排序（从大到小）是：O、R、A、I、D和M；浙江卷大致分布（从大到小）为：O、R、I、A、D和M。可以发现，14套高考数学卷均注重考查数学运算，其次才是逻辑推理、直观想象和数学抽象，这和学业质量标准具有一定的差异，学业质量标准强调数学抽象的考查，而将数学运算放在第3的位置上。

2.研究建议

（1）量化学业质量标准，使教评有章可循

分析发现，只有1/7的试卷和课程标准具有统计学意义上的一致性。虽目前学业质量标准根据内容主题细化成六素养三水平，但对于具体界定没有明确表述，这致使试卷命制者对试题的把握存在一定困难，导致试卷与学业质量标准的一致性存在一定偏差。《标准》的学业质量标准以核心素养和表现水平为基准，展现学生学业成就的关键特征，应当具有一定的操作性和科学性。1

（2）调整内容主题比例，实现评标一体化

根据分析结果可知，4套高考数学卷内容主题的分布与学业质量标准具有一定的差异性。在新高考改革背景下，教育评价更应贴合课程标准。从2020年开始，教育部考试中心不再制定普通高等学校招生全国统一考试的大纲。2 所以，要将教育课程改革与高考综合改革相结合，实现教、学、评的一致性。3在日常教学中，要以《标准》作为风向标，不断研读学业质量标准，调整各内容主题比例，营造有利于学生可持续发展和终身学习的环境。

（3）把控认知表现水平，完善学业评价体系

分析发现，12套试卷的表现水平与学业质量标准存在一定差异。学业质量标准提供了一个基于数学核心素养的评价框架，但仍需在命题路径、方法、试题结构和评分细则等方面进行缜密探索，构建一个严谨完备的学业评价体系，研发出相关的教育检测工具。4通过改进学业评价体系，试题命制中适当增强认知表现水平2的考查，关注个体差异性，从而发展学生的学习能力，为中国教育现代化培养出创新型人才。5

（4）均衡核心素养分布，令命题合理科学

14套高考数学卷核心素养的考查与学业质量标准的一致性表现各有差异。高考测评中需注重核心素养的均衡分布6，重视数学核心素养的评估和考核，加强学业质量标准与学业评价的适切度，可以适当增强试题中数学抽象，以此优化评价方式，培养学生在数学领域的必备品格和关键能力，让他们运用数学抽象的思维方式来分析问题。

（5）研制本土一致性评价工具，贴合我国国情

尽管我国在试题和课程标准的一致性研究方面进行了一些探索，但主要采用的是美国的研究工具1，本研究也主要采取SEC模型。在学业质量标准中，应以核心素养为导向，以高考命题改革为立足点，以更适切的研究工具来研究高考试题与学业质量标准的一致性。因此，我国亟须开发一套符合中国实际的本土化研究工具，不仅能检测学生的核心素养和对知识的掌握程度及其水平，而且为教育发展和人才选拔起到重要作用。2

Study on the Consistency between College Entrance Examination Mathematics Paper and Academic Quality Standards under the Background of the New College Entrance Examination Reform

—Taking the 2017-2023 Shanghai and Zhejiang College Entrance Examination Papers as an Example

WU Jiamin，LIN Zizhi，SHI Tianran

（1.Institute of Community for Chinese Nation，Central South Minzu University，Wuhan Hubei，430074；

2.College of Big Data Science，Jiangxi Normal University of Science and Technology，Nanchang Jiangxi，330013）

Abstract： In the context of the New College Entrance Examination and the New Curriculum Standards， the college entrance examination papers are important indicators of education reform. Using the SEC consistency model， this study constructs an analysis framework based on content themes and academic quality standards to study 14 sets of college entrance examination mathematics papers from Shanghai and Zhejiang， the first batch of pilot provinces， from the three dimensions of content themes， performance levels， and core literacy of academic quality standards. Based on the findings， suggestions are provided to improve the alignment between examination papers and academic quality standards：1.quantify academic quality standards to guide teaching and evaluation; 2. adjust the proportion of content themes to achieve integration of assessment standards; 3.control the cognitive performance levels to improve the academic assessment system; 4. balance the distribution of core literacy for reasonable and scientific examination design; 5. develop local consistency assessment tools to align with the national conditions.

Key words： New College Entrance Examination，New Curriculum Standards，academic quality standards，College Entrance Examination Mathematics Papers，consistency