基于DEA-SBM超效率和Malmquist-Luenberger指数的中国工业绿色经济增长核算研究

赵祺 陈媛媛 张秀娟

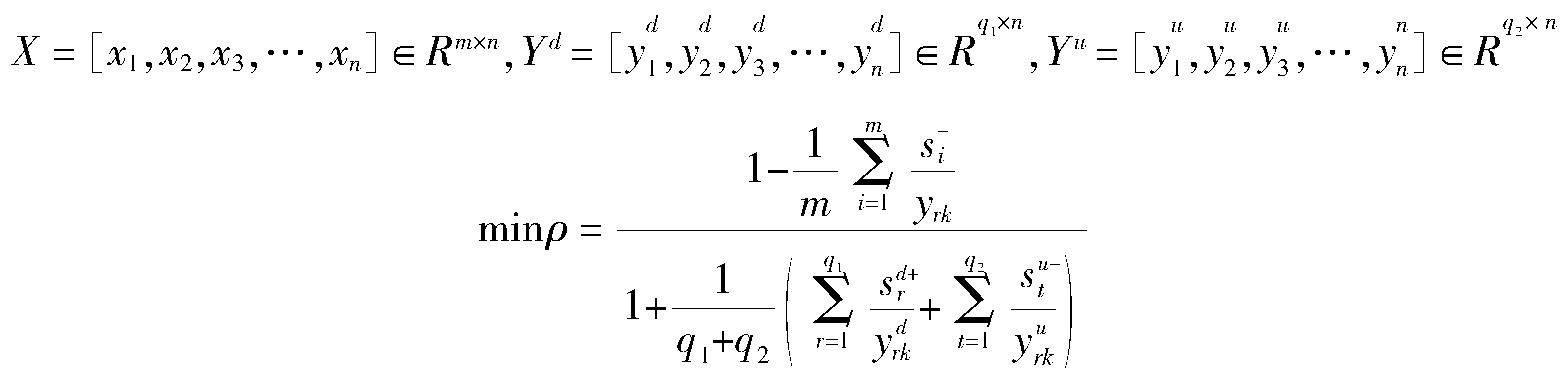
摘要：以1997～2020年我国30个省的数据为研究样本，分析中国各省市工业企业的绿色经济效率的影响因素。研究表明：我国各省市工业技术效率各地区间差异巨大。各省市工业绿色生产资金投入大都存在不足，资金管理水平也不高。因此，地方政府应坚持区域协同发展，相互借鉴学习，吸收总结经验。在资本积累的基础上应加强对生态环境质量的投资，发挥绿色技术外溢效应。

关键词：DEA模型；绿色经济；地区工业；增长核算

中图分类号：F426.2;F224      文献标志码：A      文章编号：1008-4657（2024）03-0044-11

绿色经济增长是指在发展经济的同时也发扬绿色发展理念，并将环境、资源、人口三者紧密结合，实现经济与绿色的经济增长双赢。随着社会的不断发展进步，高能耗、高污染的传统经济增长模式弊端逐渐暴露，以绿色低碳为主导的理念逐渐融入生产，加速着产业结构和经济结构的优化升级。习近平总书记明确指出，要以能源低碳发展为关键，坚持走生态优先、绿色低碳的发展道路。然而，长久以来，我国将GDP的高速增长作为经济发展的主要目标，这样的体制机制短时间很难转变，也制约着工业经济的高质量发展。为此，运用DEA-SBM超效率和Malmquist-Luenberger指数模型对我国各省的绿色经济增长进行核算，把握各省绿色经济发展现状，提高工业环境效率和资源利用率，对推动中国工业绿色经济向快向好发展有重大意义。

通过相关文献搜索，DEA模型大多用来计算效率与进行评估，目前真正运用于计算经济增长比较少见。绿色经济增长的核算采用DEA模型的研究较少，因此，本文着重介绍DEA模型下地区绿色经济增长核算的研究，为今后的绿色经济增长等方面的计算研究提供一定理论基础。因此，本文以1997～2020年我国30个省的数据为研究样本，基于DEA-SBM超效率和Malmquist-Luenberger指数对中国工业绿色经济增长核算进行研究。

一、文献综述

社会发展是一个不断进步的过程，经济的不断发展带动绿色经济的深入推进，绿色经济逐渐成为经济发展的中流砥柱，这是必然趋势。因此越来越多的学者对绿色经济增长的核算给予了高度关注。例如，崔铁宁等运用超效率SBM模型对首都经济圈的13个城市的绿色经济圈能源效率进行了分析；戴辞源等通过采用超效率SBM模型研究安徽省各城市循环经济的效率水平；卢新海等借助非期望产出超效率SBM模型对城市土地绿色利用效率进行刻画和识别；王少剑采用超效率SBM模型得出中国城市碳排放的时空动态演变特征，并预测其未来发展的趋势［ 1-2 ］。

通过文献研究与分析，不难发现已有研究仍有需完善之处。作为绿色经济系统理论的创建者和实践者之一，北京工商大学世界经济研究中心主任、遂宁绿色经济研究院院长季铸教授就对绿色经济（Green Economy）进行了如下定义［ 3 ］：社会形态、增长方式以及经济结构的基本内容为生态农业、循环工业和持续服务产业，绿色经济的发展目标就是持续、和谐和效率。绿色经济包含一种全新的三位一体思想理论和发展体系，其中的目标体系、结构体系和发展体系分别为“效率、和谐、持续”三位一体，“生态农业、循环工业、持续服务产业”三位一体，“绿色经济、绿色新政、绿色社会”三位一体。

文章采用SBM超效率和Malmquist-Luenberger指数将期望和非期望产出都考虑进去，研究绿色经济增长的核算，构建SBM超效率和Malmquist-Luenberger指数模型作为标准，以中国各地区绿色经济增长作为实例，对中国整体绿色经济增长核算进行研究。

二、研究模型与指标数据

（一）数据包络分析（DEA模型）概念

学者Charnes和Cooper在“相对效率评价”概念的基础上提了DEA模型，即数据包络分析（Data Envelopment Analysis）。这个模型对多投入、多产出的研究对象进行相对效率评价，是在数量经济学非参数的基础上建立的［ 6 ］。该模型主要根据调查得到的有效样本数据，利用数学函数的方法计算所研究的效率，用计算出的效率来衡量研究对象。将相对无效率的研究样本放入在有效的研究样本所形成的曲线范围中，各个研究对象的相对效率在［0，1］区间内分布，效率值为1研究样本就处在先进的位置。使用该模型不仅能够对统一研究对象的效率得分进行计算，而且能够对研究对象按照效率得分的高低进行排序，进而分析得出研究对象的资源配置与产出之间的关系。DEA模型不需要事先对研究对象具体计算函数的形式进行相关假设。DEA模型主要运用在绩效评价、生产率、效率分析，在社会学、经济学、管理学中有着广泛的运用。

（二） DEA模型的选择

传统DEA模型包括BCC模型和CCR模型，属于角度和径向的度量方法，由于传统DEA模型没有充分考虑到产出与投入的松驰性问题，因此只能同比例改变投入产出量以此提高效率，使得效率评价结果不是很精确。DEA-SBM模型引入松弛变量，并考虑到非合意产出，可以克服传统DEA模型存在的偏差问题，可以对工业绿色效率进行更为精准的测度。DEA-SBM模型主要用于静态衡量工业绿色效率，在分析历史面板数据和数据的变化趋势方面还存在明显不足。为了更全面分析工业绿色效率的变化趋势和影响因素，我们选择Malmquist-Luenberger指数（ML指数）动态分析工业绿色效率变化趋势与影响因素，Malmquist-Luenberger指数是DEA计算中常用的指数，Malmquist-Luenberger指数考虑到非合意产出，能用来揭示全要素生产率的动态演变特征，同时能通过分解指数探寻造成全要素生产率提高或下降的原因，适合用于动态分析工业绿色效率影响因素。因此，本文选择DEA-SBM模型与Malmquist-Luenberger 指数从静态和动态两个方面共同分析工业绿色效率，旨在核算出工业绿色效率及影响因素。

（三）SBM超效率模型

SBM超效率模型将中国各年各省份的工业经济活动系统视为决策单元，首先运用SBM模型来对所有工业经济单元进行效率测度，然后针对其中有效的决策单元再采用SBM超效率模型进行进一步测度。包含非期望产出的SBM模型则可表述为：假设中国各省份工业经济活动系统中有n个独立的决策单元（称DMUj ， j  =  1·2·3…n），每个决策单元对应的工业经济活动系统中m（i  =  1·2·3…q1）种工业投入x，q1（r  =  1·2·3…q1）种工业期望产出yd；q2（t  =  1·2·3…q2）种工业非期望产出yu。S，S，S分别表示投入松弛、期望工业产出松弛和非期望工业产出松弛调整量，λj为权重。定义投入产出矩阵：

在规模报酬可变的情况下，以上投入产出组合的生产能集可表示为P  =  {（x， yd， yu） | x ≥ Xλ， yd ≤ Ydλ，yu ≥ Yuλ}，此处为权重向量。考虑非期望产出的SBM模型的表达式如下：

被评价决策单元的效率值为 ρ *，其为以上模型的最优解，同时从投入和产出两个角度来对无效率值进行测度。 ρ *  =  1，说明决策单元相对有效，0  <   ρ *  <  1，说明决策单元是相对无效的。

考虑非期望产出的超效率SBM模型的表达式如下：

（四） Malmquist-Luenberger指数

假设第k个决策单元在t时期的投入产出组合表示为 （xtk，y，y），则需要求解如下线性规划表达式。

其中，i  =  1，2，3，…，m，r1  =  1，2，3，…，q1，r2  = 1，2，3，…，q2，t  =  1，2，3，…，T，λ≥0，表示在t时期横截面的观测值权重。

基于以上方向性距离函数，可以构造第K个决策单元t到t+1时期的ML指数。

ML， EFFCH，TECH分别表示第K个决策单元从t到t+1时期的全要素生产率变动指数、技术效率变化指数和技术进步变动指数。ML > 1，表示工业绿色全要素生产率增长；ML = 1，表示工业绿色全要素生产率不变；ML < 1，表示工业绿色全要素生产率下降。TECH刻画了整个工业生产前沿面的整体移动与变化即工业生产技术的变化情况，通常是指产业技术进步、先进技术的开发与引进、宏观政策优化和市场大环境等方面因素。TECH > 1，TECH = 1和TECH < 1，分别反映了工业绿色生产技术进步、不变和衰退。主要用来对决策单元向环境技术前沿面的追赶和逼近效应进行刻画，反映对前沿绿色生产技术的充分利用情况、实际生产情况的改善使得决策单元逼近“最佳实践者”。EFFCH > 1，EFFCH = 1，EFFCH < 1分别表示工业绿色技术效率提升、不变与下降。

技术效率变动指数（EFFCH）可分解为纯技术效率变动指数ML = PECH·SECH·TECH和规模效率变化指数SECH 。即，EFFCH = PECH·SECH·TECH，因此有：ML = PECH·SECH·TECH公式（5）。

其中，PECH > 1，PECH = 1，PECH < 1，分别表示工业经济纯技术效率水平提高、不变与下降。SECH为规模效率（规模效应）的变化即与最适规模的匹配程度的变化。SECH> 1，SECH= 1，SECH<1，分别表示工业经济规模效率水平的提升、不变与降低。

（五）指标选取及数据来源

本文选取1997～2020年中国30个省（自治区、直辖市）（港澳台及西藏地区由于数据缺失，故未列）数据计算工业的绿色经济效率，具体的指标选取及数据来源如下：

1.投入要素指标

（1）资本投入。资本投入使用资本存量来衡量，可通过永续存盘法来计算，具体方法为：

Kt = Kt-1（1 - δt）+It

其中：Kt为第t年的固定资本存量，δt为第t年的折旧率，It为第t年的新增投资额。折旧率δt用第t年的累计折旧与（t - 1）年的累计折旧之差比上第t年的固定资产原价，其中第t年的累积折旧用当年的固定资产原值减去当年固定资产净值得出。最后根据PPI（生产者价格指数）对计算出的固定资本存量进行平减，将数据转化为以1997年为基期的固定资本存量。

（2）劳动投入。采用第t年各行业规模以上工业企业的年平均就业人数。

（3）能源投入。采用各省工业行业企业能源消耗总量来衡量能源投入。

2.产出要素指标

（1）期望产出。文章中的期望产出直接采用各省规模以上工业总产值，基期为1997年，进行数据的平减。

（2）非期望产出。文章用熵值法将工业三废（废水、废气、废渣）这三类污染指标拟合成一个综合污染指数，将此作为测度各省的绿色经济效率的非期望产出。方法如下：

计算i省的综合污染指数vi = ajΣPij，即为综合污染指数。

本文数据均来源于历年的《中国工业统计年鉴》《中国统计年鉴》《环境统计公报》和《中国环境统计年鉴》以及国泰安数据库。

三、DEA模型下中国地区工业绿色经济增长核算实证研究

（一）描述性统计

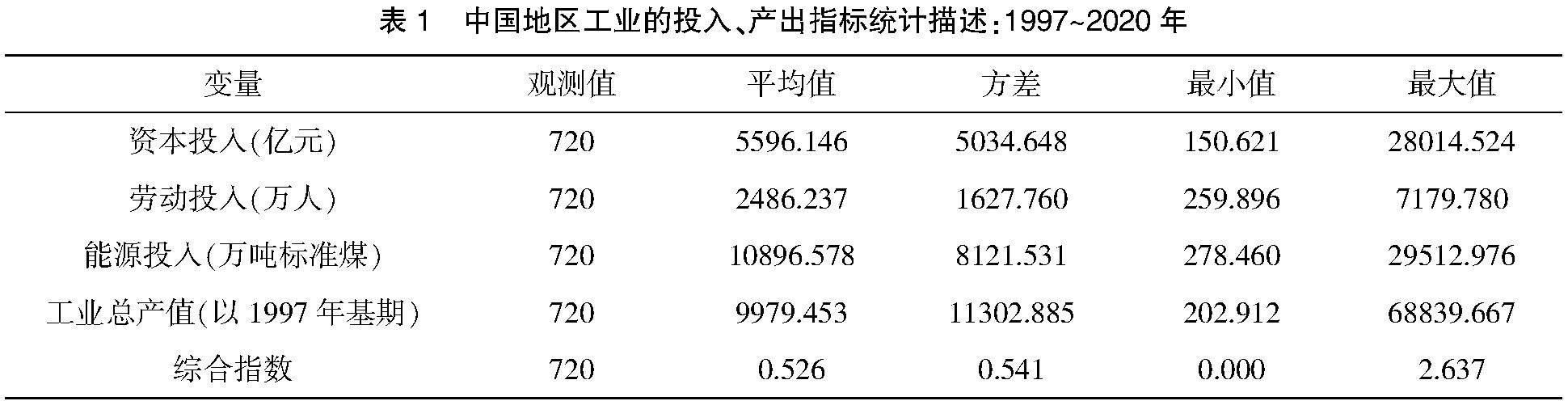
文章运用上文建立的DEA模型，以地区工业为实例，对绿色经济的增长进行核算，其中，利用固定资产投资价格指数和GDP平减指数，分别对各年的增加值和固定资产净值年平均余额进行平减，以1997年为基期，对应的计算数据结果如表1所示。

分析表中的数据可以发现，中国各省份的工业发展情况在1997～2020年期间，不但情况各不相同，而且发展情况有很大的差异。但是，表中反映的期望产出最大最小值比都在1000左右，非期望产出也是如此，所有投入变量的最大最小值之间数值差异极大，巨大的数值差异证明了，中国各地区工业的增长速度各不相同，经济规模差异十分显著，各地区对环境污染的重视和处理的程度也不一样。

（二）SBM超效率结果分析

各年各省份的超效率结果分析都可以运用中国地区工业在1997～2020年间的投入—产出数据集进行计算得出，具体结果如表2所示。

1.从中国各地区的绿色经济发展的技术效率平均综合指数来看，各地区发展水平具有较大差异（见图1）。具体来说，上海工业发展效率较高，平均综合指数为1.740；河南地区居中，平均综合指数为0.344；青海技术效率最低，平均综合指数为0.011，未达到DEA有效，所以，需提高工业技术水平，优化工业程序和设计，提高工业发展效率。

2.中国各地区工业绿色经济发展技术效率综合指数的均值为0.535，未达到DEA有效且水平并不高，说明各地区仍需在节能减排、发展绿色经济上加大力度。

3.工业发展水平与工业技术效率没有太大的关系。各省份工业发展的技术效率综合指数基本都很低，同时不同省份间的综合指数有着明显的差别。具体来说，在1997～2020年中国各地区工业投入产出平均综合指数为1的省份个数总体来看，不到总数的一半。

4.这些结果直观地反映了一些问题。首先，由于发展工业时的生产技术超出或低于自身经济发展条件，没有找到最佳的方式，导致工业生产的技术效率处于不高的水平。其次，正是技术效率低下，改善的空间也很大，经济发展上升的空间也随之变大。但实际上，经济发展中，只要将自己所有的技术最有效率的运用，那么技术效率就为1。这就是为什么有些省份明明经济发展很落后，但是却能运用符合自身发展的技术就可以把技术效率提高的原因。

5.这些结果也让我们深思背后原因。随着我国经济的不断发展，经济模式不断转型，各省份的工业技术效率也在不断改变。大多数省份的技术效率得到了改善，根据数据统计，这样的省份共有18个，包括天津、重庆、宁夏、河北、湖北、江西、黑龙江、云南、安徽、贵州、河南、吉林、湖南、四川、新疆、陕西、内蒙古以及海南，排列顺序是按工业技术效率由小到大排列的［ 12 ］。也有部分省份，主要是在一线生产的省份，技术效率基本维持不变，比如北京、上海、江苏、山东、广西和西藏，它们的技术效率都维持在1。技术效率恶化方式，确保城市的技术效率一直保持着最大值［ 4 ］。

为了促进经济的增长，保持技术效率恶化的现象仍然存在。例如青海、甘肃、浙江、广东、山西、辽宁以及福建等省份。导致这种差异的原因主要有以下几点：

第一，技术效率明显改善的省份。这些省份在经济发展初期，技术效率也不高，但是经过经济转型和技术升级，创造出适合自身发展的工业环境，找到适合自身发展的实践技术，提高了工业生产的效率，技术效率自然而然得到了改善。

第二，技术效率保持在1的省份。这些省份出现这个状况可能有两点原因，要么经济发展中工业技术一直在不断创新保持在前沿的水平，要么经济发展中所使用的工业技术与自身经济条件达到了高度的一致性，相互间的配合趋于完美。在这样的条件下，技术效率水平保持在1也无可厚非。这两种类型的省份将自己所拥有的技术最大可能地进行高效率利用，这从侧面证明，正确运用技术能够推动经济社会的不断发展。城市应当及时根据经济发展的需要不断改善技术水平，不断根据需求调整技术，紧跟社会发展脚步。这些省份积极引进了先进的技术，但是忽视了自身经济发展的规律，没有正确评估自身经济的承受力，无法与先进技术相匹配，使得发展条件跟不上先进技术需要的条件，技术效率下降也可想而知。还有一种可能是，本身可以与技术相匹配的条件水平降低，造成相互间的不合适，匹配度降低，技术效率自然不可能上升，恶化也是正常［ 13 ］。

（三）中国地区工业绿色经济增长核算的因素分解及指数分析

运用中国31个省份在1997～2020年间的投入—产出数据，以1997年作为基年，运用上文建立基于方向性函数的DEA模型，再结合其他相关辅助公式计算，对中国各地区工业绿色经济增长的全要素生产率指数进行分解，分析从1998年至2020间数据，具体如表3、表4所示。

观察上列数据，不难得出以下结论：

1.中国各省市在1997～2020各年间绿色发展总体呈向好趋势，技术进步指数TC均大于1，技术进步明显，SEC指数值除重庆市外均小于1，说明中国各省市工业绿色生产资金投入大都存在不足，资金管理水平也不高。除黑龙江、江西、青海、新疆四个省份的综合技术效率变化指数EC小于1，其他27个省份的综合技术效率变化指数EC均大于1，说明大多数省份工业绿色生产技术转化效率较为平稳。

2.工业绿色全要素生产率MI均大于1，工业绿色发展总体呈向好趋势，其主要原因是工业绿色生产技术转化效率不高、资金投入和资金管理存在疏漏。但仍然存在技术转化效率不高、资金投入不足和资金管理水平不高等问题。

3.各省份工业劳动生产率的增长得益于投入资本的深化、完成效率的变化和专业技术的进步。在这三者中，效率的变化对工业劳动生产率的增长影响最小，技术的进步比效率对工业劳动生产率的增长大一些，但是这两者都没有资本的深化对工业劳动生产率增长的影响大，甚至两者相加所带来的影响都不及资本深化所带来的影响大。具体来说，在整个分析期间内，劳动生产率平均提高了一倍多。

4.各省份促进劳动生产率增长的资本深化、技术效率变化和技术进步等要素差异十分明显。从上述数据中观察各个因素的指数大小，可以发现MLKC的波动幅度在MLEC、MLKC、ML和MLTC这四种中是最大的，则将资本深化对劳动生产率增长起到决定性作用进行了更直观的反映。

四、研究结论与启示

文章以中国31个省份为研究对象，选取1997～2020年数据研究中国各地区工业环境效率水平。采用DEA模型和SBM-Undesirable模型从静态角度分析中国各省份工业环境效率，并进行空间格局的分析；借助Maimquist-Luenberger指数通过分解，分析影响工业环境效率的因素，揭示我国绿色经济发展的现状。结果表明：

1.1997～2020年中国各省市工业技术效率平均综合指数从大到小差异较大，其中上海的工业技术效率平均综合指数均值最大，为1.740；而青海的工业技术效率平均综合指数均值最小，仅0.011。两者差距达158倍，地区间差异巨大。

2.中国各省市在1997～2020各年间绿色发展总体呈向好趋势，技术进步明显，各省市工业绿色生产资金投入大都存在不足，资金管理水平也不高。大多数省份工业绿色生产技术转化效率较为平稳。

3.工业绿色发展总体呈向好趋势，其主要原因是工业绿色生产技术转化效率不高、资金投入和资金管理存在疏漏。但仍然存在技术转化效率不高、资金投入不足和资金管理水平不高等问题。

4.中国各省市全要素生产率呈上下波动态势，技术进步预期贴合度较高，是影响工业环境效率的关键因素，因此提高技术进步有利于促进工业环境效率的提升。

基于以上研究结果，提出以下建议：

1.中国各省市在促进经济发展的同时，不能为追求经济水平的快速上升而忽略了环境的保护。地方政府要以新的发展理念为指导，加强对地区工业经济发展的指导与调控，在资本积累的基础上加强对生态环境质量的投资。注重对工业发展绿色指标考核，倒逼企业开展绿色生产技术研发与利用，促进工业企业转型升级。

2.科技发展能提高企业的运行效率，先进设备能加强对工业污染物的治理和循环再利用。工业企业应该注意提升自主创新能力，推动绿色制造水平的提升，坚持绿色发展导向，依靠技术创新提升企业对绿色生产创新技术的追赶效应，提升工业绿色全要素生产率。

3.坚持区域协同发展，各省市经济发展水平和生态质量均有差异，相互之间应借鉴学习，吸收总结经验，努力提高自身的生态质量，发挥绿色技术外溢效应。

此外，应重视新技术、新模式与新能源的示范与推广，推动资源、创新技术和人才等资源的优化配置与有序流动。

参考文献：

［1］耿刘利，王琦，黎娜，等.高质量发展背景下安徽省工业绿色全要素生产率评价研究——基于SBM超效率模型与Malmquist-Luenberger指数［J］.滁州学院学报，2020，22（5）：58-65.

［2］黄明明.基于Global-Malmquist-Luenberger模型的中部6省农业绿色全要素生产率研究［J］.湖南农业科学，2022，445（10）：88-92.

［3］赵杨秋，何刚，阮君，等.基于SBM-Malmquist-Luenberger模型工业环境效率研究［J］.河北环境工程学院学报，2021，31（6）：30-36.

［4］牛晓奇，石风光.基于方向性距离函数的绿色经济增长核算——以河南省工业为例［J］.信阳师范学院学报（自然科学版），2013，26（4）：531-534.

［5］李爽，周天凯，樊琳梓.长江经济带城市绿色发展及影响因素分析［J］.统计与决策，2019，35（15）：121-125.

［6］吕品，卢东子，肖明月，等.中国工业绿色经济效率的测度及其影响因素研究［J］.浙江理工大学学报（社会科学版），2018，40（6）：561-568.

［7］陶宇，杨铭.长江经济带绿色经济增长影响因素研究［J］.重庆科技学院学报（社会科学版），2022， 275（4）：57-65.

［8］董钰涵.经济增长目标约束对中国工业绿色全要素生产率的影响研究［D］.昆明：昆明理工大学，2022.

［9］孙玉阳，尹云龙.中国绿色经济增长的水平测度及影响因素研究［J］.党政干部学刊，2021，394（10）：73-80.

［10］陈勇智，梁文明，林迎星.创新驱动我国省域绿色增长的空间效应［J］.中国环境科学，2022，42（2）：971-981.

［11］过东琴，许学军.中国绿色经济效率的测度与评价研究［J］.中国物价，2023，405（1）：33-36.

［12］王淑贺，王利军.环境规制效率和绿色经济效率耦合的时空格局及影响因素［J］.兰州财经大学学报，2021，37（3）：78-89.

［13］孙威，董冠鹏.基于DEA模型的中国资源型城市效率及其变化［J］.地理研究，2010，29（12）：2155-2165.