初中数学探究式教学

年如科

探究式教学是初中数学高效的教学方式之一，其本质是以学生为中心，以师生互动、生生互动为主要活动方式，将原本的讲解课堂变为学生的主动探究活动，尝试以学生思考为主、教师讲解为辅助的学习方式，逐渐提升初中生的数学学习能力，达到培养学生数学学科核心素养的目标。

【案例内容】

人教版八年级下册“17.1勾股定理”。

【教材分析】

勾股定理是初中几何板块内容中最重要的定理之一，在七年级以及八年级上册已经接触过三角形边角关系，以及三角形全等的内容；本堂课是在已有知识的基础上，以直角三角形为例，进行直角三角形三边等量关系的探究。通过本堂课的学习，学生对直角三角形会有更加深刻的认识，对后续的三角函数等内容的学习也能产生积极影响。不仅如此，勾股定理在数学学科以及其他学科，甚至日常生活中也有广泛应用，通过探究式课堂教学能够将多领域的知识衔接起来，帮助学生深入掌握勾股定理的相关内容，达到学以致用的最终目标。

【教学目标】

1.经历三角形三边衍生正方形面积之间的等量关系，并表示直角三角形之间的等量关系，体会转化思想。

2.经历勾股定理证明过程，理解赵爽运用“出入相补法”证明勾股定理的思路，体会数形结合思想，发展学生的逻辑推理能力，培养学生的民族自豪感。

3.掌握勾股定理的运用，并能够解决数学问题。

4.能用数学语言提出猜想，并通过例题的学习学会用数学语言表达。

【教学方法】

创设情境引入法、引导发现法、讲练结合法。

【教学过程】

一、情境导入

教师：同学们，上学期我们已经接触过三角形，了解了三角形的一些性质，对直角三角形也有过一些初步的探究，那么谁记得直角三角形的三个角有什么关系？

预设：三个角的和是180°，其中一个角为90°，另外两个角互余。

教师：非常好，那么你们知道三角形的三条边关系也非常有趣吗？接下来我们以等腰直角三角形为对象，看看它们究竟有什么关系？（此环节，教师还可以绘制关于三角形知识的思维导图，从边和角两方面对其进行知识的梳理，然后在直角三角形处留出相应的空白，等待学生自主探究，在课堂结束时让学生将思维导图补充完整。）

（设计意图：从三角形知识的复习入手，通过复习直角三角形三个角的关系，唤醒学生已有的知识经验，随后通过思维导图展示整个三角形的知识体系，引导学生明确此板块知识的上下位关系，并提出后续要探讨的话题，使学生明确本堂课的学习目标。）

二、新课讲授

（一）故事引导，初步探究

教师借助多媒体教学工具，将教材中的图片及文字以讲故事的形式呈现出来。

教师：同学们，在今天的课程学习之前，我们先来听一个小故事：相传在2500年前，毕达哥拉斯在朋友家做客时，低头发现朋友家的地砖很有趣，于是看着地板陷入了沉思。同学们来看大屏幕上出现的地砖图（见教材图17.1-1），如果你是毕达哥拉斯，你有什么样的发现呢？（为了增加学生的学习兴趣，教师还可以添加一些毕达哥拉斯的小故事，引导学生积极投入。）

预设：学生1：奶奶家的地板砖也是这种正方形的，每块方砖被分成了四个小三角形。

学生2：我发现，四个小三角形是一模一样的。

学生3：我发现两个相邻的三角形可以组成一个直角三角形，而且还是等腰直角三角形。

教师：同学们观察得非常细致，每块方砖都分成了四个完全一样的小三角形，然后两个三角形能够拼成一个等腰直角三角形，我们用正方形彩纸折纸的时候是不是有过这样的经历呢？你还有什么发现呢？

学生4：我发现相邻的相同颜色的三角形还可以组成一个小正方形……

（此时教师将上述两组对话中学生发现的现象用不同的颜色标注出来，然后继续提问）

教师：非常棒，那么这组图形之间又有一个什么图形呢？（出示教材图17.1-2）

学生：它们中间夹了一个小的等腰直角三角形。

教师：接下来，以小组为单位来分析一下，上面三种颜色的图形之间有什么关系吗？

学生以小组为单位，通过小组合作观察图片，对三种颜色图形的边长进行推测：

关系1：两个蓝色正方形的面积之和等于红色正方形也就是一块方砖的面积。

关系2：蓝色正方形的边长等于中间黄色等腰直角三角形的直角边边长。

关系3：红色正方形的边长等于中间黄色等腰直角三角形的斜边边长。

通过小组合作，学生对三种颜色图形的关系有了初步了解，但是没有学生想到将两者结合起来研究三边关系，此时教师可以继续追问：

教师：同学们表述得非常棒，那有没有想过将这两个结论合并起来呢？来尝试一下吧！

随后，学生以小组为单位，对三组图形的面积关系进行分析，发现结论：两个蓝色小正方形的面积和等于一个红色大正方形的面积。

教师：你们能不能用数学化的语言表达出来呢？

预设：以等腰直角三角形两直角边为边的小正方形的面积的和，等于以斜边为边长的大正方形的面积。

教师：换句话说就是“等腰直角三角形中，两直角边的平方和等于斜边的平方”。这就是勾股定理的雏形。

（设计意图：本环节是初步探究环节，以师生互动探究为主，以毕达哥拉斯故事为引导，激发学生参与课堂活动的兴趣。整个活动以教师为主导，学生为主体，充分培养学生观察、发现问题的能力，让学生学会用数学的眼光观察、思考、表达现实世界。）

（二）研讨分析，深入探究

教师：同学们，刚刚我们发现了等腰直角三角形三边之间的关系，那么你们觉得其他直角三角形的三边关系符合这一规律吗？（提出本环节需要探讨的中心问题，引导学生继续探究。）

学生以小组为单位，可以先进行结论的猜测，如有的小组认为符合，有的小组认为不符合，根据自己猜测的结果进行后续探究。

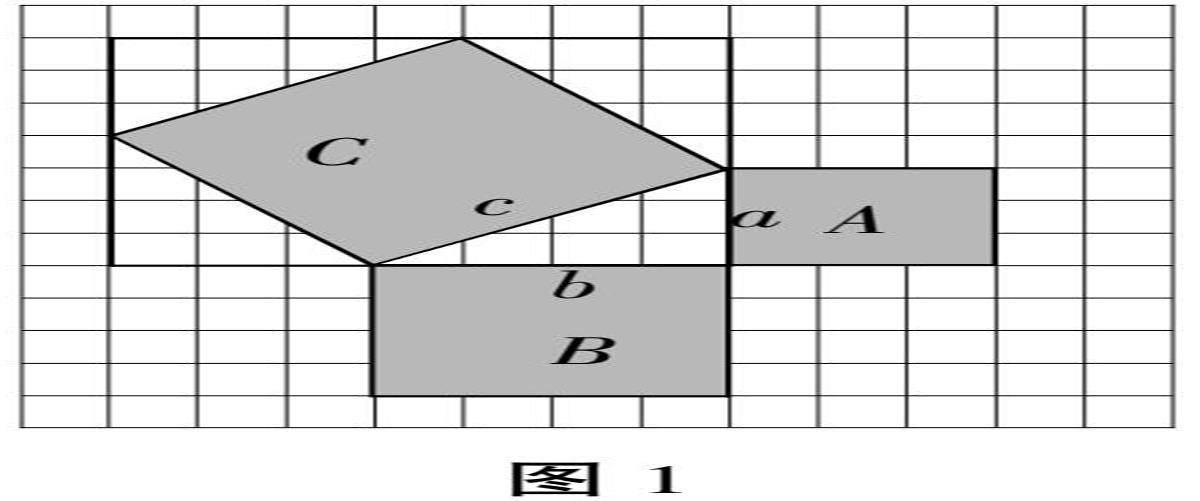
问题：（出示图1，小正方形的边长为单位1）你能计算出大正方形C的面积吗？

学生观察图形，结合自己现阶段掌握的面积计算方法，思考并计算正方形A、B、C的面积，如割补法等。学生探究如下：

步骤一：SA=3×3=9，SB=4×4=16

步骤二：正方形C不能用边长乘以边长的计算方法，但是我们可以按照其四个顶点的位置将它补充为一个新的正方形，然后利用计算面积。新正方形的面积为7×7=49，然后再减去周围四个小三角形的面积：3×4÷2×4=24，最终得出正方形C的面积为25。

教师：那么图中三个正方形的面积有什么关系呢？它们是否和毕达哥拉斯发现的关系一样呢？是否具有与等腰直角三角形三边为边长的正方形面积同样的等量关系呢？

学生：SA+SB=SC，具有与等腰直角三角形三边为边长的正方形面积同样的等量关系。

此时如果学生能提出疑问：网格中的三角形可以代表所有的三角形吗？学生就可以按照这个思路继续深入探讨，如果不能，教师提出问题：那你们觉得刚刚老师给出的图形能不能代表所有直角三角形的情况呢？一般直角三角形符合吗？（教师继续出示教材中的图片。）

教师：假设现在直角三角形三边为a、b、c，两条直角边分别为a、b，斜边为c，那么a2+b2=c2是否成立呢？（在引导学生问题探究中，教师可以根据学生探讨的过程给出分层支持。）

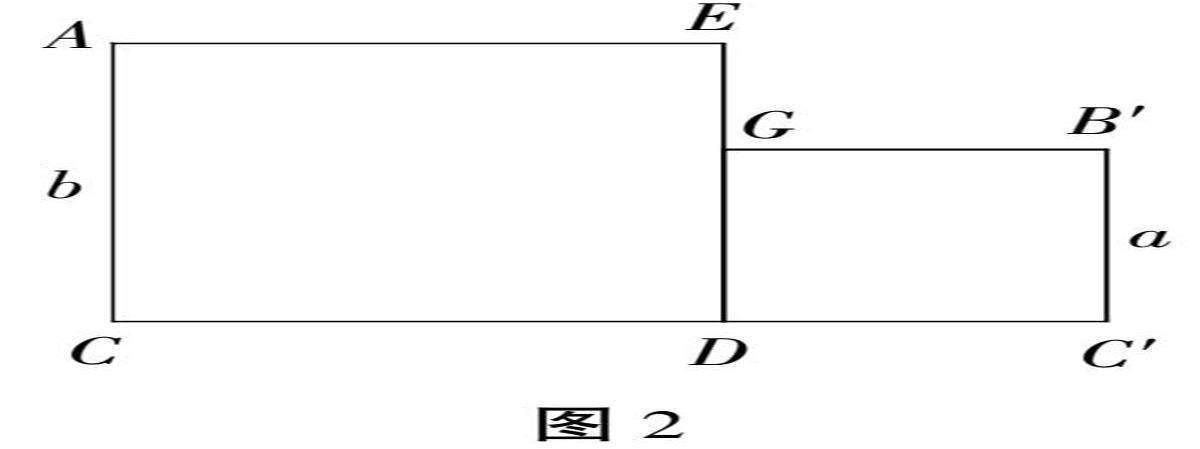
支持一——摆放图形：结合上述三角形三边关系，摆放两个边长分别为a和b的正方形，其中一边重合（见图2），引导学生计算出这两个图形的面积。

学生根据教师的提出摆放出两个正方形，然后根据面积公式计算出两个正方形的面积为a2和b2。

支持二——分割图形：引导学生在两个正方形中切割出两个直角三角形，确保切割出的三角形一个顶点重合，然后得出边长c，随后证明左右两个三角形全等，以及以B点为两条c边的夹角为直角（见图3）。

学生根据教师给出的支持性问题，在底边上找到符合要求的B点，然后通过做辅助线的方式，借助三角形全等以及其他相关知识验证教师提出的问题，最终用含有ab的式子表示所有数量关系。

支持三——重新拼接组合：如何找到大正方形的另一组邻边，即找到以直角三角形斜边为边长的正方形？

学生根据教师的支持，小组合作借助前两个环节探究所得的图形进行切割、拼剪，然后展示自己小组得出的成果。

此时教师可以追问：为什么按这种方式拼出的四边形是正方形？你能说明理由吗？（预设：学生通过直角三角形两个锐角互余等知识点说明新得出的四边形是正方形。）

支持四：那么你能证明新得出的边长为c的正方形和原来图形的面积没有变化吗？

学生整理上述三个环节得出含有ab的算式，然后进行计算、分析，最终证明：a2+b2=c2。

（设计意图：此环节师生探究活动中，教师运用类比思想引导学生对问题进行探讨，这是数学研究从特殊到一般的过程。在四个步骤的支持中，教师搭建脚手架，一步步引导学生在质疑、思考、分析、探讨过程中，自然、合理地发现知识前后之间的联系，从而体会“出入相补法”的原理。）

【教学反思】

探究式教学是初中数学教学中常用的教学方法之一，以往数学教学中，教师始终认为学生的学习能力、探究能力较弱，并没有尝试将整堂课全部教给学生，此次以学生为主体的课堂探究学习尝试中，教师作为主导者，适时提出问题，搭建学生小组合作观察、思考、探究的“脚手架”，既保证了学生学习的兴趣和积极性，又确保了整堂课按照教师设计的思路进行。此外，在整个课堂中学生小组合作占据主体地位，小组内的交流、思考、合作活动相对较多，学生能够将与三角形相关的知识系统串联起来，也有利于自身知识体系的搭建，为后续更复杂的数学知识学习奠定基础。

（作者单位：甘肃省康乐县上湾民族中学）

编辑：陈鲜艳