基于染色算法的地震干涉成像技术

李振春 刘畅 曲英铭 苏琳淞 丁泽政 陶同熠

摘要：为了提高基于染色算法的逆时偏移计算效率，提出基于染色算法的地震干涉成像技术（CC-STRTM）。地震干涉技术作为一种炮记录的处理手段可以消去两个炮记录中相同的信号。该技术将观测系统从地表下移到人为选取的地下校准面，将研究区域缩小到校准面下侧。再分析干涉成像结果，选出染色区域。最后完成复数域的逆时偏移处理，输出虚部偏移结果。通过复杂模型对该方法进行测试，对比分析成像结果和计算效率。结果表明，该方法在提高成像精度的同时不降低计算效率。

关键词：地震干涉成像； 染色算法； 逆时偏移； 盐下构造； 计算效率

中图分类号：P 631.4   文献标志码：A

文章编号：1673-5005（2024）03-0037-07   doi：10.3969/j.issn.1673-5005.2024.03.004

Seismic interferometric imaging based on staining algorithm

LI Zhenchun1，2， LIU Chang1，2， QU Yingming1，2， SU Linsong3， DING Zezheng1，2， TAO Tongyi1，2

（1.State Key Laboratory of Deep Oil and Gas， China University of Petroleum（East China）， Qingdao 266580， China;2.School of Geosciences in China University of Petroleum（East China），Qingdao 266580， China;3.Zhidan Oil Production Plant， Yanchang Oilfield Company Limited， Yanan 717500， China）

Abstract： To enhance the computational efficiency of reverse time migration（RTM） using the staining algorithm， this paper proposes  seismic interferometric imaging based on the staining algorithm（CC-STRTM）. Seismic interferometry technique， applied to shot records，eliminates the same signals in two shot records. This technique shifts the observation system down from the surface to an artificially selected subsurface datum surface， focusing on the lower side of the datum surface for analysis. The seismic interferometric imaging identifies the stained areas， facilitating RTM processing in the complex domain and generating imaginary part migration results. The proposed method usdergoes testing using a complex model to compare and analyze the imaging results and computational efficiency. The results indicate that the method enhances imaging accuracy without compromising computational efficiency.

Keywords： seismic interferometric imaging; staining algorithm; reverse time migration（RTM）; subsalt structure; computational efficiency

Kirchhoff叠前时间偏移［1］在工业上已被广泛应用，但计算精度不如逆时偏移。逆时偏移的优点是可适用于复杂模型，缺点是计算量大。通过优化交错网格可以提高求解波动方程的计算效率［2-3］。随着对勘探精度要求的提升，逆时偏移需要考虑起伏地表［4］、边界反射［5］、差分系数［6］、弹性介质［7］、横向各向同性（VTI）介质［8］、偏移速度场［9］、三维成像［10］、最小二乘反演［11］等问题。在石油勘探地震资料处理中，常见的技术有溶洞型储层地震特征分析［12］、储层自相控反演［13］、检波组合目标函数优化［14］、储层地震反射特征研究［15］、反Q滤波方法研究［16］、时移地震定量解释［17］、地震干涉技术［18］。地震干涉是基于光学的学科［19］，是地震处理中的一项经典技术。其目的是模拟出震源点和检波点都在地下基准面的地震数据［20-21］。基准面通常选取在更接近研究目标的区域。地震干涉主要应用在校正垂直地震剖面（VSP）数据，以适应不规则地表采集或覆盖层中复杂地质结构对成像的影响，如低速层或横向变化剧烈的地层。其目的是产生单井剖面数据，使其更容易处理，并更好地“照亮”地下目标地质体［22］。地震干涉可以将震源转移到检波点所在的位置，反之亦然。它可以将观测系统从地表下移到地下基准面。Zhao等［23］提出了一种基于小波域交叉相关的地震干涉方法，以抑制伪影和噪声。Guo等［24］开展了一种同步反演方法，它可以同时反演覆盖层速度模型与基准面处的炮记录。后来又探索了一种面向目标的反演工作流程［25］，结合了全波形反演和最小二乘法重校准。Barrera等［26］提出了一种新的方法，只使用反卷积来减少地震干涉中没有物理意义的干扰波。Liu等［27］将匹配滤波器和超级干涉测量法结合起来，从实际资料中恢复出面波。盐下成像一直是个难题，近几年有一种新的解决思路［28］，该思路引入了发育生物学中的命运映射的概念。通过对已知目标地质体染色，在波场中追踪目标地质体处发生的反射波，进而单独对目标地质体成像。该算法将波动方程从实数域推广到了复数域。复数域里的实部波场与传统波场一样，虚部波场里未被染色的目标地质体是透明的。通过限制染色时间提高计算效率，减少噪音串扰，提高成像质量［29］。虚部波场的振幅与实部波场的振幅相差几个数量级，因此虚部波场的波形扭曲，而广义染色算法保持了虚部波场的振幅，提高了信噪比［30-31］。广义染色算法存在的问题是虚部波场里的地震波波前面到达染色地质体时，会产生和波场传播方向相反的干扰波［32］。笔者将基于互相关型地震干涉的双重校准技术与基于染色算法的逆时偏移技术相结合，形成一套基于染色算法的地震干涉成像处理技术，验证该算法的成像效果和运算效率。

1 方法原理

1.1 地震干涉原理

频率域的波动方程可写为

ρi（ρ-1i（p，pA，ω））+ω2c2（p，pA，ω）=-jωρδ（p-pA）.（1）

式中，ρ为介质密度；ω为角频率；p为震源激发点；pA为信号接收点；δ为单位阶跃函数；i为在pi方向的偏导数;G为格林函数。

点A处的上行波场可写为

-A（p，pA，ω）=R（p，pA，ω）sA（ω）.（2）

点A处的下行波场可写为

+A（p，pA，ω）=δ（p-pA）sA（ω）+r-A（p，pA，ω）.（3）

式中，sA（ω）为震源谱；r为自由地表的反射系数；R（x，xA，ω）为非均匀介质的反射响应，包括所有层间多次波和自由表面多次波。完整的格林函数是直达波和反射波的叠加，可写为

fullA（p，pA，ω）=（p-pA）sA（ω）+r（+A（p，pA，ω）+-A（p，pA，ω））.（4）

相关类型的互易定理［33］可写为

h（pB，pY，ω）=∮D-1jωρ（x）（*（pX，pY，ω）i（pX，pB，ω）-i*（pX，pY，ω）（pX，pB，ω））nid2p，（5）

h（pB，pY，ω）≡（pB，pY，ω）+*（pB，pY，ω）.（6）

式中，B、Y、X为观测系统中3个不同位置。

方程（5）表达的含义是在X点激发Y点接收的信号中消去X点激发B点接收的部分，产生B点接收Y点接收的信号。这一过程可以用图1（a）到图1（c）表示，即消除图1（a）中的图1（b）所体现的部分，得到图1（c）。图1中S0为地表，S1为人为选取的地下校准面，符号“五角星”为震源，符号“倒三角”为检波点。为了得到图1（e）所示的地下激发地下接收的信号，还需要提供图1（d）所示A点激发Y点接收的信号。

-（pA，pY，ω）=R（pA，pY，ω）sA（ω），（7）

+（pA，pY，ω）=δ（p-pA）sA（ω）+r-（pA，pY，ω），（8）

full（pA，pY，ω）=（pA-pY）sY（ω）+r（+（pA，pY，ω）+-（pA，pY，ω））.（9）

震源侧的观测系统下移和检波点侧的观测系统下移可以用双重校准干涉方程表示：

h（pB，pA，ω）=∮D-1jωρ（x）（∮D-1jωρ（x）×（*XYiXB-i*XYXB）*nid2p·iAY-i∮D-1jωρ（x）（*XYiXB-i*XYXB）*nid2p·AY）nid2p.（10）

上述过程均在频率域中进行，后期的成像处理选用逆时偏移，在时间域内完成。

因此需要将做一步傅里叶逆变换的处理：

R（x，t）=ifft（h（pB，pY，ω））.（11）

式中，R为地震干涉得到的炮记录。

由于观测系统从地表下移到地下，所以新得到的炮记录不含校准面上方的地质体信息。因为方程（10）的输入信号和输出信号长度一致，所以输出信号的下侧必然会有很多无效零值。这部分信号对后期成像无效，因此在后期的成像处理前可只提取出有效信号部分，并且在成像处理时只需要输入校准面下侧的速度模型。这将从时间维度和空间维度减少运算量。下列方程可表示从炮记录里抽取有效信号的过程：

Rbottom（x，t）=∑tmax0R（x，t），（12）

tmax≈（1-DdaDnz）T.（13）

式中，T为输入信号的长度；Dda为校准面深度；Dnz为模型纵向深度；R为地震干涉得到的炮记录；bottom为校准面下方的模型。

1.2 基于染色算法的地震干涉成像方程

基于染色算法的逆时偏移在虚部波场中不含非目标结构的反射波，因此可以得到高信噪比的目标区域成像结果。复数域的波动方程可写为

2（（x）+i（x））t2=（（x）+i（x））2Δ（（x）+i（x））+（（x）+i（x）），（14）

x∈As， （x）=10-6，（15）

xAs， （x）=0。（16）

式中，符号“-”为实数场；符号“～”为虚数场；符号“Δ”为拉普拉斯算子；p为声压；t为时间；v为速度；s为震源；As为染色区域，也就是目标区域。方程（15）和（16）解释了虚部速度场包含染色区域和非染色区域两部分。

将方程（14）拆分为实部波动方程和虚部波动方程：

2（x，t）t2=2（x）Δ（x，t）+（x），（17）

2（x，t）t2=2（x）Δ（x，t）+2i（x）（x）Δ（x，t）.（18）

虚部场是和实部场一起激发的，虚部震源可写为

（x）=2（x）（x）Δ（x，t）.（19）

基于染色算法的成像方程可写为

Iim_all（x）=∫T0all（x，t）Rall（x，T-t）dt.（20）

式中，下标im为虚部场，I为偏移结果，all为全模型。

由于地震干涉得到的炮记录不含校准面上方的信号，因此后期的染色逆时偏移只需在校准面下方的模型中完成。因此基于染色算法的地震干涉成像方程可写为

Iim_bottom（x）=∫tmax0bottom（x，t）Rbottom（x，T-t）dt.（21）

图2为基于染色算法的地震干涉成像流程。

2 模拟数值测试

图3为复杂模型。该模型尺寸为4000 m×4000 m，横向采样点数为400个，纵向采样点数为400个。横向、纵向采样间隔均为10 m。共激发40炮，炮间距为100 m，检波点间距为10 m，最大采样时间为4 s，采样间隔为1 ms，震源主频为20 Hz。校准面选择在深度为2440 m处。该模型成像的关注点用黑色虚线框出。

图4为地震干涉需要的输入地震响应，图4（a）对应于图1（a），图4（b）对应于图1（b），图4（c）对应于图1（d）。图5（a）为地震干涉得到的炮记录，对应于图1（e），图5（b）为用来验证方法正确性的真实情况下的地震响应。通过对比图5（a）和图5（b），可以看出地震干涉技术成功地将观测系统下移到校准面，得到的炮记录和真实情况下的炮记录相似。从图5中可以看到1500 ms以下均为零值。因此可抽取出1～1500 ms的信号完成逆时偏移处理。

图6为成像结果对比。可以看到图6（b）和图6（c）中的盐下成像效果较差，本来不与盐丘相交的地层此时与盐丘相交。因此选择这一区域进行染色，也就是图6（a）。图6（d）的盐下成像效果较好，还原出了与盐丘贴近的地层界面，其成像效果等价于图6（e）。染色算法中虚部波场固有的微量串扰导致了少量偏移假象，但这并不影响对成像结果的分析。偏移假象分布在染色区域外部，杂乱无章。

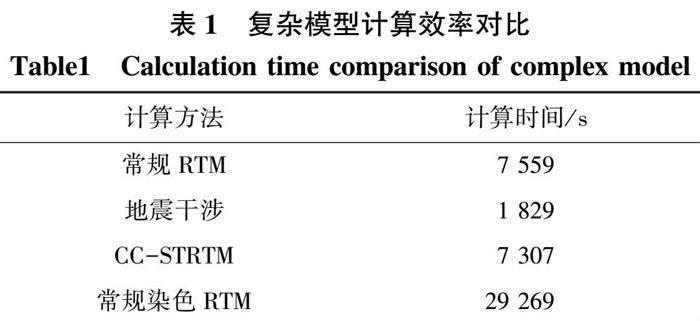
表1对图6（b）到图6（e）的计算效率进行了对比。可以看出基于染色算法的地震干涉成像的计算效率略大于常规RTM，小于地震干涉成像，约为常规染色RTM的4倍。这证明了本文中采用地震干涉技术提高了基于染色算法的逆时偏移的计算效率。

3 结 论

（1）地震干涉技术作为一种针对目标区域成像的技术，可以将观测系统从地表移到地下校准面，得到的炮记录不含校准面上方的地质体信息。抽取出炮记录的有效信号部分，输入校准面下方的速度模型完成逆时偏移成像处理。

（2）对传统逆时偏移成像结果的模糊区域进行染色，采用基于染色算法的逆时偏移技术进行成像，可得到高质量的成像效果，但计算效率约为常规逆时偏移的1/4。

（3）提出的基于染色算法的地震干涉成像技术不仅在成像效果上等价于常规染色逆时偏移，而且在计算效率上约等于常规逆时偏移，这也就意味着在提升计算精度的同时不降低计算效率。

参考文献：

［1］ 刘立彬.VTI介质角度域Kirchhoff叠前时问偏移方法［J］.中国石油大学学报（自然科学版），2012，36（5）：51-55.

LIU Libin. Angle-domain Kirchhoff prestack time migration approach in VTI media［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2012，36（5）：51-55.

［2］ 方刚，FOMEL Sergey，杜启振.交错网格Lowrank有限差分及其在逆时偏移中的应用［J］.中国石油大学学报（自然科学版），2014，38（2）：44-51.

FANG Gang， FOMEL Sergey， DU Qizhen. Lowrank finite difference on a staggered grid and its application on reverse time migration［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2014，38（2）：44-51.

［3］ 雍鹏，黄建平，李振春，等.优化的时空域等效交错网格有限差分正演模拟［J］.中国石油大学学报（自然科学版），2017，41（6）：71-79.

YONG Peng， HUANG Jianping， LI Zhenchun， et al. Forward modeling by optimized equivalent staggered grid finite difference method for timespace domain［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2017，41（6）：71-79.

［4］ 黄建平，杨宇，李振春，等.基于M-PML边界的Lebedev网格起伏地表正演模拟方法及稳定性分析［J］.中国石油大学学报（自然科学版），2016，40（4）：47-56.

HUANG Jianping， YANG Yu， LI Zhenchun， et al. Lebedev grid finite difference modeling for irregular free surface and stability analysis based on M-PML boundary condition［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2016，40（4）：47-56.

［5］ 王永刚，邢文军，谢万学，等.完全匹配层吸收边界条件的研究［J］.中国石油大学学报（自然科学版），2007，31（1）：19-24.

WANG Yonggang， XING Wenjun， XIE Wanxue， et al. Study of absorbing boundary condition by perfectly matched layer［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2007，31（1）：19-24.

［6］ 黄建平，娄璐烽，彭炜颋，等.一种基于拉格朗日乘子的空间域差分系数优化方法［J］.中国石油大学学报（自然科学版），2022，46（4）：30-40.

HUANG Jianping， LOU Lufeng， PENG Weiting， et al. An optimization method of finite difference coefficient in spatial domain based on Lagrange multipliers［J］. Journal of China University of Petroleum（Edition of NaturalScience），2022，46（4）：30-40.

［7］ 李振春，雍鹏，黄建平，等.基于矢量波场分离弹性波逆时偏移成像［J］.中国石油大学学报（自然科学版），2016，40（1）：42-48.

LI Zhenchun， YONG Peng， HUANG Jianping， et al. Elastic wave reverse time migration based on vector wavefield separation［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2016，40（1）：42-48.

［8］ 乐友喜，陈艺都，吴佳伟，等.自适应整形正则化迭代最小二乘谱反演方法［J］.中国石油大学学报（自然科学版），2022，46（3）：54-61.

YUE Youxi， CHEN Yidu， WU Jiawei， et al. Iterative least squares spectrum inversion based on adaptive shaping regularization［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2022，46（3）：54-61.

［9］ 国运东，黄建平，李庆洋，等.基于混叠数据多步长优化提高全波形反演的运算效率［J］.中国石油大学学（自然科学版），2019，43（2）：45-52.

GUO Yundong， HUANG Jianping， LI Qingyang， et al. Improving computation efficiency of full wave form inversion based on multi-step preferred optimization in multi-source domain［J］.Journal of China University of Petroleum （Edition of Natural Science）， 2019，43（2）：45-52.

［10］ 李庆洋，黄建平，李振春，等.基于Ll范数正则化的三维多震源最小二乘逆时偏移［J］.中国石油大学学报（自然科学版），2019，43（4）：52-59.

LI Qingyang， HUANG Jianping， LI Zhenchun， et al. 3D multi-source least-squares reverse time migration based on Ll norm regularization［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2019，43（4）：52-59.

［11］ 梁锴，曹丹平，孙上饶，等.VTI介质地震波群速度三维扩展各向异性线性近似表征［J］.中国石油大学学报（自然科学版），2021，45（6）：51-59.

LIANG Kai， CAO Danping， SUN Shangrao， et al. Extended anisotropic linear approximation for seismic wave group velocity in 3D VTI media［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2021，45（6）：51-59.

［12］ 胡宇霆.时移岩石物理图版在时移地震定量解释中的应用［J］.西南石油大学学报（自然科学版），2022，44（6）：21-28.

HU Yuting. Application of rock physical template in the time-lapse seismic quantitative interpretation［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2022，44（6）：21-28.

［13］ 张全，王一品，张伟，等.地震波能量补偿的并行反Q滤波方法研究［J］.西南石油大学学报（自然科学版），2023，45（1）：24-32.

ZHANG Quan， WANG Yipin， ZHANG Wei， et al. Research on parallel inverse Q filtering methods for seismic wave energy compensation［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（1）：24-32.

［14］ 代瑞雪，郗诚，冉崎，等.复杂岩性背景下储层地震反射特征研究［J］.西南石油大学学报（自然科学版），2023，45（2）：21-31.

DAI Ruixue， XI Cheng， RAN Qi， et al. A study on seismic reflection characteristics of reservoir under complex lithology background［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（2）：21-31.

［15］ 彭更新，徐峰，徐凯驰，等.基于宽频子波的检波组合目标函数优化方法［J］.西南石油大学学报（自然科学版），2023，45（2）：32-42.

PENG Gengxin， XU Feng， XU Kaichi， et al. An objective function optimization method based on multi-frequency wavelets for receiver combination in seismic acquisition［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（2）：32-42.

［16］ 王宗俊，田楠，范廷恩，等.复杂断裂系统浊积储层自相控反演技术研究［J］.西南石油大学学报（自然科学版），2023，45（2）：43-57.

WANG Zongjun， TIAN Nan， FAN Tingen， et al. Self-facies-control pre-stack inversion technology for turbidite sandstone reservoir with complex fault system［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（2）：43-57.

［17］ 郑多明，汪家洪，肖又军，等.基于地震数值模拟的溶洞型储层地震特征分析［J］.西南石油大学学报（自然科学版），2023，45（6）：57-68.

ZHENG Duoming， WANG Jiahong， XIAO Youjun， et al. Seismic characteristics analysis of carst cavity reservoirs based on seismic numerical simulation［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（6）：57-68.

［18］ CLAERBOUT J. Synthesis of a layered medium from its acoustic transmission response［J］. Geophysics， 1968，33（2）：264-269.

［19］ BARRERA P， SCHLEICHER J， VAN DER NEUT J. Limitations of correlation-based redatuming methods［J］. Journal of Geophysics and Engineering， 2017，14（6）：1582-1598.

［20］ BERRYHILL J R. Wave-equation datuming［J］. Geophysics， 1979，44（8）：1329-1344.

［21］ BERRYHILL J R. Wave equation datuming before stack［J］. Geophysics，1984，49（11）：2064-2067.

［22］ WAPENAAR C P A， COX H L H， BERKHOUT A J. Elastic redatuming of multicomponent seismic data［J］. Geophys Prospect， 1992，40（4）：465-482.

［23］ ZHAO Y， LI W C. Wavelet-cross correlation-based interferometric redatuming in 4D seismic［J］. Geophysics， 2018，83（4）：Q37-47.

［24］ GUO Q， ALKHALIFAH T. Datum-based waveform inversion using a subsurface-scattering imaging condition［J］. Geophysics， 2019，84（4）：S251-S266.

［25］ GUO Q， ALKHALIFAH T. Target-oriented waveform redatuming and high-resolution inversion： role of the overburden［J］. Geophysics， 2020，85（6）：R525-36.

［26］ BARRERA D F， SCHLEICHER J， BRACKENHOFF J. Interferometric redatuming by deconvolution and correlation-based focusing［J］. Geophysics， 2021，86（1）：Q1-13.

［27］ LIU J H， DRAGANOV D， GHOSE R. Reducing near-surface artifacts from the crossline direction by full-waveform inversion of interferometric surface waves［J］. Geophysics， 2022，87（6）：R443-R452.

［28］ CHEN B， JIA X F. Staining algorithm for seismic modeling and migration［J］. Geophysics， 2014，79（4）：17-26.

［29］ LI Q H， JIA X F. Time-partition staining algorithm for target-oriented migration［C/OL］//2015 SEG Annual Meeting， New Orleans， Louisiana， October 18-23［2023-02-14］. https：//doi.org/10.1190/segam2015-5888935.1.

［30］ LI Q H， JIA X F. An efficient generalized staining algorithm for imaging weekly illuminated area［C/OL］//2016 SEG Annual Meeting，New Orleans， Louisiana， October 16-21［2023-02-11］. https：//doi.org/10.1190/hpc2016-026.

［31］ LI Q H， JIA X F. Generalized staining algorithm for seismic modeling and migration［J］. Geophysics， 2017，82（1）：17-26.

［32］ LI Y X， JIA X F. Target-oriented dual-domain staining strategy for high-quality elastic wave imaging［C/OL］// 2019 SEG Annual Meeting， San Antonio， Texas， September 15-20［2023-02-12］.https：//doi.org/10.1190/segam2019-3215706.1.

［33］ WAPENAAR K， FOKKEMA J. Greens function representations for seismic interferometry［J］. Geophysics， 2006，71（4）：SI33-SI46.

（编辑 修荣荣）

基金项目：国家自然科学基金项目（42074133，42174138）；中国石油天然气股份有限公司重大科技合作项目（ZD2019-183-003）；中国科协青年人才托举计划（YESS20200237）；中央高校基本科研业务费专项（22CX07007A）

第一作者：李振春（1963-），男，教授，博士，博士生导师，研究方向为地震波正演及偏移成像。E-mail：leonli@upc.edu.cn。

通信作者：曲英铭（1990-），男，教授，博士，博士生导师，研究方向为双复杂构造正演模拟、建模与成像，复杂海洋环境地震成像，黏介  质、各向异性介质模拟与成像，多分量弹性波成像，可控震源特殊噪声压制。E-mail：quyingming@upc.edu.cn。

引用格式：李振春，刘畅，曲英铭，等.基于染色算法的地震干涉成像技术［J］.中国石油大学学报（自然科学版），2024，48（3）：37-43.

LI Zhenchun， LIU Chang， QU Yingming， et al. Seismic interferometric imaging based on staining algorithm［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2024，48（3）：37-43.