指向学生运算能力培养的小学数学结构化教学策略

罗礼红

摘要：培养运算能力有助于学生理解运算的算理，寻求合理、简洁的运算途径解决问题。“运算律”是与小学数学整数四则混合运算领域有关的重要内容，是培养学生运算能力的关键。教师要站在整体、系统、结构的高度把握和处理教材，引导学生充分感受和把握数学的知识结构和方法结构，体验数学知识体系的发展过程。

关键词：整体构建；本质；结构化；运算能力

《义务教育数学课程标准（2022年版）》（以下通称“新课标”）指出，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。“运算律”是北师大版小学数学教材四年级上册第四单元的内容，是与小学数学整数四则混合运算领域有关的重要内容，是培养学生运算能力的关键。这个单元不仅是对整数四则混合运算进行总结性学习和梳理混合运算的运算顺序，也是对运算律意义与简便运算的系统学习和对算式的等值变形的感受。两者互相依存，同等重要，勾勒出此单元在整个小学数学“数与代数”领域的核心地位。教材注重混合运算中运算顺序与运算律的联系与区别，运算顺序是关于运算的一般规则，运算律是等值变形实现合理简便计算的特殊规则，一般规则与特殊规则巧妙编排在一起，能让学生全面看待运算问题，对运算有整体认识（见下页图1）。

教师要站在整体、系统、结构的高度把握和处理教材，引导学生充分感受和把握数学的知识结构和方法结构，体验数学知识的发生发展过程。笔者所在的团队开展了“运算律”单元知识的结构化教学实践研究，旨在探索结构化教学的多维路径。

一、关联知识原点，奠定结构根基

数学知识之间有着天然的结构上的联系，旧知是新知的基础，新知是旧知的发展，环环相扣，组成互相联系的整体，即“结构”。四则运算的意义、加法验算、问题解决等成为运算律知识的生长点。教

师在“运算律”单元教学中需要自身建立结构化认知，促使学生头脑中新知、旧知融合共生。

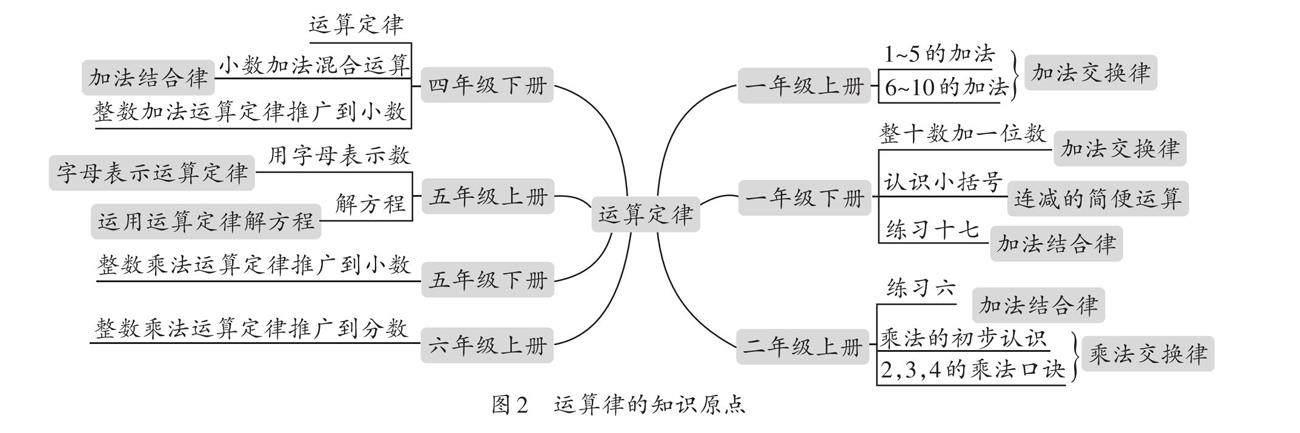
在一至三年级的学习中，运算律都是以具体的生活实例出现。学生在探索计算方法和解决简单的实际问题的过程中凭直觉运用，早已经将运算律自然渗透。也就是说，运算律是运算的基础算理，曾反复出现在整数运算中（见图2）。

例如，在“乘法分配律”一课中，教师可引导学生思考：我们今天学习的乘法分配律，其实早已经默默地出现在我们的学习中，如学习乘法口诀时，学习两位数乘一位数、三位数乘两位数时，都用到了拆分计算的原理，其实就是乘法分配律。这样，能让学生学习的知识一脉相承，有利于相互关联，重构意义，实现认识结构化。

二、梳理关键知识，形成结构全貌

本单元可提炼为如下页图3所示的知识结构，主要学习整数四则混合运算、加法和乘法的运算律、运用运算律进行简便运算三个方面的内容。从内容框架分析，四则混合运算和中括号的认识，是对小学领域混合运算进行了概括，是小数、分数混合运算的基础；五个运算律学习的意义是理解及简便计算，借助运算律及数据特点改变了运算顺序，但运算结果没有改变。

从思维框架分析，学生在探索、辨析中理解四则混合运算的方法多样性，增强对运算意义的理解，提高运算能力；在探索运算律的过程中积累合情推理的思维经验。

从内容编排分析，五个运算律的编排结构基本一致，即观察算式→仿写算式→解释规律→表述规律→应用规律，让学生发现问题、确认发现、提出问题、归纳结论，积累合情推理的数学活动经验，提升思维能力。

从核心素养分析，学生在探索运算规律中培养符号意识、模型思想、推理能力；在应用规律进行简便运算、解决生活中的问题时，培养数感、运算能力、应用意识等核心素养。可见，本单元的学习能考查学生多项数学核心素养，具有非常重要的学习价值。

在实施结构化教学的过程中，教师应通过关联知识原点、整体构建结构、搭建结构“承重墙”，打断结构“隔断墙”，设计有效的教学活动和课中作业，形成运算律教学改进策略，最终达成“运算律”教学结构化，促进学生形成结构化思维（见图4）。

三、凸显意义教学，把牢结构主脉

教师要抓住数学本质，沟通知识之间的内在联系，凸显数学内容的系统和结构（见表1）。

【教学片段】在乘法分配律中突出意义

师：刚才同学们没有经过计算，怎么就知道教材中的两个算式是相等的呢？

生：因为左边的数和右边的数都是相同的。

生：举例子，第一个算式左边先是4 + 6=10，再乘9，就是10个9；右边是6个9加4个9，加起来也是10个9，因此不用计算就能知道它们相等。

生：第二个算式左边先是71 + 29=100，再乘18就是100个18，右边是71个18加29个18，加起来也是100个18，所以不用算就能知道它们相等。

师：例子是举不完的，通过分析几个几的意思，借助乘法运算的意义，就能知道两边的算式相等（出示图5）。

学生举例验证乘法分配律时，往往采用计算来验证，但实际上也可以采用观察来验证，突出对意义的理解及表达，夯实结构中的核心支点。通过表1可知，连减性质和乘法分配律改变了计算方法，但结果不变，这就需要学生去理解意义。加法结合律和乘法结合律改变的是运算顺序，运算和数据都没有增减或变化。这样，当面对题目125 × 8 × 4和（125 + 8） × 4时，学生就不会有太多的误解。

四、激活简便计算，实现结构迁移

（一）分类梳理，整理简便运算的编排结构

从教材编排的19道典型的简便计算题可以看出，仅有4道题作为新授中的例子出现，其余大多数出现在练习中。加法、乘法结合律的题型较为完善，加法、乘法交换律则缺乏及时的练习，减法性质也缺乏完整的探究。乘法分配律有11道典型的简便计算题，涉及乘法分配律的逆向运用、变式的乘法分配律、拆数再运用、对减法分配等，将部分难点类型穿插到5个运算律的综合练习题中，未能聚焦分析，增加了学生的理解难度。

（二）对比辨析，厘清简便运算的关键结构

教师可将乘法分配律的典型题目独立出来，加强与乘法结合律的辨析，加强乘法分配律（对减法分配）的学习，设计“光看就能算”“分开与合拢”“对比出真知”等活动，充分发展学生的数感，让学生或观察凑整，或灵活拆分，基于算理理解简便运算。

【教学片段】乘法分配律

在运用乘法分配律时，不少学生把它理解为求两个积的和，忽略了乘法分配律适用的一个重要条件：有一个相同的乘数。为此，笔者设计了这样的两道题进行对比。

（1）36 × 69 + 37 × 69

（2）36 × 69 + 37 × 49

师：这两个算式有什么相同点和不同点？

生：相同点都是求两个积的和。

生：不同点在于（1）有相同的乘数，（2）没有。

师：请你将两个算式与乘法分配律进行对比，有什么发现吗？

生：（1）可以用乘法分配律，（2）不能。

通过这样的对比，学生认识到用乘法分配律的一个重要条件是：必须有一个相同的乘数。

同理，乘法分配律与乘法结合律也特别容易混淆，学生需要结合实例，如（125 × 25） × 8和（125 + 17） × 8，重点对比并辨析三个问题：两个运算律的意义有何不同？什么时候改变运算顺序？怎么改变运算顺序？在此基础上，再进行其他运算定律的综合练习（见图6）。

（三）实例运用，优化简算的认知结构

结合生活实例的运用，学生积累了简便运算与解决问题结合的经验，更有利于理解运算律，将运算律与生活实例进行联系，让简便运算的结构迁移。遇到类似的实例时，学生会判断与辨析，会选择合适的方法解决问题，会灵活运用运算定律，增强应用能力。

在实施结构化教学的过程中，教师要引导学生通过关联知识原点、整体构建结构，搭建结构“承重墙”，打断结构“隔断墙”，促使“运算律”教学结构化，形成结构化思维。通过单元结构化的整体教学， 能有效地提升学生的学习能力，发展学生的数学核心素养。

参考文献：

［1］凌乾川，周波，周婷.建造“关联性”图谱实施“结构化”教学：以小学数学“数与代数”结构化教学为例［J］.四川教育，2020（Z4）.

［2］朱俊华，吴玉国.基于单元整体的小学数学结构化教学［J］.中小学教师培训，2019（9）.

（责任编辑：杨强）