基于改进Weibull模型的高强缝合锚钉缝线强度预测
李新娅 王宁 卢佳浩 张鹏 夏兆鹏 侯耒


DOI: 10.19398j.att.202309018
摘 要:为消除缝合锚钉缝线在使用过程中存在断裂的风险,以8.3 tex超高分子量聚乙烯纤维为原材料,采用编织工艺制备了单层编织缝线和轴向衬纱双层编织缝线。为了研究其力学性能,选择8、16、24、32、40、48 mm隔距对单纤维的断裂强力进行测试,选择50、200 mm隔距对8.3 tex复丝的断裂强力进行测试,选择200 mm隔距对单层编织缝线和轴向衬纱双层编织缝线的断裂强力进行测试。对纤维的直径和缝线中纤维与轴向夹角的角度进行测量。采用两参数Weibull模型和改进Weibull模型对单纤维、8.3 tex复丝和单层编织缝线的断裂强度进行预测。结果表明:单层编织缝线的断裂强力为299.8 N,轴向衬纱双层编织缝线的断裂强力高达393.0 N。对8.3 tex复丝和单层编织缝线的断裂强度进行预测,改进Weibull模型的预测值准确度高。高强骨锚钉缝线的强力比同类型医用缝线更高,改进Weibull模型可对高强缝合锚钉缝线的强力进行精准预测,实现了从单纤维到复丝再到纱线的断裂强度预测,可为医用缝线结构设计和力学性能分析提供理论依据。
关键词:缝合锚钉缝线;超高分子量聚乙烯;断裂强力;两参数Weibull模型;改进Weibull模型;强度预测
中图分类号:TS101.2
文献标志码:A
文章编号:1009-265X(2024)06-0052-09
收稿日期:20230914
网络出版日期:20231220
作者简介:李新娅(1999—),女,天津人,硕士研究生,主要从事生物医用纺织品方面的研究。
通信作者:夏兆鹏,E-mail:xiazhaopeng@tiangong.edu.cn
在骨科手术中,软组织在骨骼上的固定是手术成功的关键一环。缝合锚钉可以简单有效地固定肌腱和韧带等软组织,是骨骼上软组织固定的主要方式[1-2]。缝合锚钉由锚钉部分和缝线部分组成,锚钉部分被植入骨头中,用于固定缝线;缝线部分用于固定软组织[1-5]。理想的缝合锚钉必须提供足够的机械稳定性,以降低手术失败的风险。缝线的强力是衡量缝合锚钉机械稳定性的重要指标,然而因缝线断裂致使锚钉失效的案例不在少数[6-8]。因此制备高强度的缝合锚钉缝线,对骨科手术具有重要意义。
Weibull分布是一种纤维强度预测成熟的表征工具[9]。脆性材料的抗拉强度变化通常用Weibull分布来表示[10],已广泛用于衡量合成纤维[11-12]和天然纤维的抗拉强度[13-14]。但传统的两参数Weibull模型的预测结果存在很大误差[15-16]。因此,一般引入多模态和三参数Weibull模型或其他改进模型来提高预测精度[16-17]。
本文以8.3 tex超高分子量聚乙烯纤维为原材料,通过编织工艺制备单层编织缝线和轴向衬纱双层编织缝线,并分析其力学性能;对单纤维、复丝和缝线的强力进行测试;对纤维的直径和缝线中纤维与轴向夹角的角度进行测量;采用两参数Weibull模型、改进Weibull模型预测缝合锚钉缝线的断裂强度,以期为医用缝线结构设计和力学性能分析提供理论依据。
1 实验
1.1 材料与仪器
8.3 tex超高分子量聚乙烯纤维(东莞市盛芯特殊绳带有限公司)。编织机(ZLPB-2A型,徐州恒辉编织机机械有限公司);电子单纤维强力仪(YM-06A型,莱州元茂仪器有限公司);
微机控制拉力试验机(WGL-2500ST,利拓检测仪器有限公司),荧光显微镜(LK40POL型,天津徕科光学仪器有限公司)。
1.2 实验方法
1.2.1 单层编织缝线的制备
采用锭子型编织机制备单层编织缝线。将8.3 tex超高分子量聚乙烯纤维绕成16组锭子之后装上编织机,机器的主要操作部分为一稳定的工作平台(立式),在平台表面设有彼此交错的切线相连的“8”字形凹槽,将锭子装在凹槽中,并分为大小相等的两个部分,彼此均匀交叉并作等速率的反向移动。如此往复,机器织出16股纱线。操作过程如下:
a)将8.3 tex超高分子量聚乙烯纤维绕上16组锭子,再将16组锭子装上机器的工作平台。
b)集合16股束纤维,穿过织口的小孔,并绕上卷筒。
c)连接电源,先按点动按钮观察运行流畅度,再按动运行按钮,进行编织。
1.2.2 轴向衬纱双层编织缝线的制备
将8.3 tex超高分子量聚乙烯纤维绕上16组锭子,装上工作平台。再将一根16股单层纱线放在16组锭子中间进行同步编织,使16组纤维在16股单层纱线表面编织形成编织层,编织出轴向衬纱双层编织纱线。
1.3 测试方法
1.3.1 单纤维强力测试
根据Textile fibres—Determination of breaking force and elongation at break of individual fibres(ISO 5079∶2020),使用电子单纤维强力仪,进行单根纤维的强力测试。分别测定8、16、24、32、40、48 mm隔距单纤维的断裂强力,拉伸速度为20 mm/min。
1.3.2 复丝和缝线强力测试
根据《高强化纤长丝拉伸性能试验方法》(GB/T 19975—2005),使用微机控制拉力试验机在两种不同条件下测试断裂强力。a)在夹持距离为200 mm、拉伸速度250 mm/min条件下,分别测量8.3 tex超高分子量聚乙烯纤维、单层编织缝线和轴向衬纱双层编织缝线的断裂强力。b)在夹持距离为50 mm、拉伸速度250 mm/min条件下,分别测量8.3 tex超高分子量聚乙烯纤维和单层编织缝线的断裂强力。
1.3.3 纤维直径变异测试
用荧光显微镜测量6种长度(8、16、24、32、40、48 mm)样品纤维的直径。因为纤维的形态是完全圆形的,所以采用圆的面积公式计算横截面面积。
具体测试方法为:每种长度的纤维各采集20个数据点,8 mm长度的纤维测试点间距为0.4 mm,16 mm长度的纤维测试点间距为0.8 mm,24 mm长度的纤维测试点间距为1.2 mm,32 mm长度的纤维测试点间距为1.6 mm,40 mm长度的纤维测试点间距为2 mm,48 mm长度的纤维测试点间距为2.4 mm。
1.3.4 缝线纤维与轴向夹角测量
用荧光显微镜观察表面形貌,并测量编织纱线表面纤维的轴向夹角θ。
2 Weibull分布统计分析
强度分布σ通常用两参数Weibull分布表示如下:
P=1-exp-VV0σσ0m(1)
式中:m为Weibull模量(或形状参数),σ0为特征强度(或尺度参数),V0为参考体积,V为纤维体积,P为纤维断裂概率。
P由式(2)计算:
P=i-an+b(2)
式中:n是测试数据的样本数,i是测试数据的序号,a和b是常数。通常情况下,0≤a≤0.5,0≤b≤1。
当纤维直径不变时,式(1)变换为:
P=1-exp-LL0σσ0m(3)
式中:L0为单位长度,L为测试隔距。
由式(3)可计算σ0的平均值:
σ-=σ0LL0-1mΓ1+1m(4)
式中:Γ表示伽马函数。
由式(4)可由L1处纤维的平均断裂强度σ1计算出L2处纤维的平均断裂强度σ2:
σ-2=σ-1L2L1-1m (5)
式中:σ1为纱线在L1处的断裂强度,cN/dtex;σ2为纱线在L2(单位为mm)处的断裂强度,cN/dtex;m为纱线的Weibull模量。因此由式(5)可以知道,测得了某个隔距长度下的纱线强度,便可以在理论上求出任意长度下的纱线强度。
根据式(3),两参数Weibull分布的线性拟合方程为:
ln[-ln(1-P)]=mlnσ-mlnσ0+lnL(6)
然而,两参数Weibull分布并不能总是准确预测纤维的断裂强度,根据式(6)得到的实验数据与计算数据存在显著差异[14]。因此,Xia等[15]对实验数据进行Weibull预测时使用γ参数对两参数Weibull方程进行了修正,并定义了γ为纤维变异系数,式(7)为两参数Weibull方程修正形式:
P=1-exp-LL0γσσ0m(7)
根据式(7),纤维的平均断裂强度可写为:
σ-=σ0LL0-γmΓ1+1m(8)
式(5)可变为:
σ-2=σ-1L2L1-γm (9)
式(6)可变为:
ln[-ln(1-P)]=γlnL-γlnL0+mlnσ-mlnσ0(10)
因此,Weibull模量和特征强度可以从ln(-ln(1-P))与ln(σ)产生的直线图中得到。
根据文献[18]以及式(7),可以得到两参数Weibull分布下束纤维断裂强度σ-b,可表示为:
σ-b=σ0(Lm)-1mexp-1m(11)
束纤维和纱线的关系可用式(12)表示:
σ-b=σ0(Lm)-1mexp-1mcos2θ(12)
改进后的Weibull分布下束纤维断裂强度σ-b可表示为:
σ-b=σ0(Lγm)-1mexp-1m(13)
束纤维和纱线的关系式为:
σ-b=σ0(Lγm)-1mexp-1mcos2θ(14)
3 结果与讨论
3.1 纤维拉伸强力
将超高分子量聚乙烯纤维在8、16、24、32、40、48 mm隔距下进行强力测试,其定速拉伸性能如表1。
由表1可以看出,超高分子量聚乙烯纤维的断裂强度随着测试隔距的增大逐渐减小。Xia等[19]测试了不同隔距下黄麻纤维的断裂强度,也得出了相同结论。这是由于测试隔距越大,使纤维发生断裂的弱节出现的概率越大。此外,纤维直径变异值也随测试隔距的增大而增大。表明超高分子量聚乙烯纤维的断裂强度不仅跟纤维本身的缺陷有关,跟纤维的直径变异也有关系。纤维直径变异系数越大,纤维的断裂强度越小。
3.2 复丝和缝线拉伸强力
将8.3 tex复丝和缝线进行强力测试,其定速拉伸性能如表2和表3所示。从表2可以看出,8.3 tex复丝拉伸性能和单纤维拉伸性能类似,断裂强度均随着测试隔距的增大而随之减小。
表3中的数据来源于文献[20-21]中的测试结果,所有的缝合线均为美国药典标准尺寸(No.2)。从表3中可以看出,本文所设计的单层编织缝线强力为299.8 N,均大于文献[20-21]中所述医用缝线的强力,改进后的轴向衬纱双层编织缝线强力高达393.0 N。
3.3 Weibull分布参数的确定
3.3.1 Weibull断裂概率P
根据式(2)和文献[22],a、b一般取值范围如表4所示。
采用Weibull方程进行预测时,被预测隔距距离预测隔距越近,其预测结果越准确[19]。为保证预测准确度,故采用测量隔距中间值24 mm隔距处测得的超高分子量聚乙烯断裂强度进行预测,根据表4中列出的4种a、b值和式(2)可计算得到断裂概率P,故根据不同的断裂概率P可以得到基于24 mm隔距超高分子量聚乙烯纤维的Weibull线性回归图,如图1所示。
4组不同a、b取值计算得到的相关系数平均值均在0.90及以上,所以ln(-ln(1- P))与ln(σ)之间具有良好线性关系。根据图1可知,当a=0、b=1,测试隔距为24 mm时超高分子量聚乙烯纤维Weibull线性回归的R2值最大(R2=0.91),此时ln(-ln(1- P))与ln(σ)线性关系最好。由于研究的是超高分子量聚乙烯的实测值,仅凭R2值的大小仍然无法推断最终断裂强度预测值的准确性。但可以根据误差的高低来判断断裂概率P式预测是否准确[22], 误差的计算公式为:
ε/%=|σ实测-σ估计|σ实测×100(15)
根据式(2)、式(5)、式(15)以及按照表4中4种a、b取值的顺序,利用24 mm隔距测得的超高分子量聚乙烯断裂强度,计算得到32、40、48 mm隔距纤维断裂强度预测值,如表5所示。
根据误差比较可得第3组别(a=0,b=1)是误差最小的情况,所以选取第3组别(a=0,b=1)来确定本文中Weibull方程的断裂概率P。
3.3.2 不同测试隔距下的Weibull线性拟合图
选取第3组别(a=0,b=1)计算得到32、40、48 mm隔距超高分子量聚乙烯纤维断裂强度Weibull线性拟合图,如图2所示。
由图2可知,R2的值均在0.89到0.99之间,可得上述4种隔距下ln(-ln(1-P))与ln(σ)之间具有良好的线性度,表明四种情况下的超高分子量聚乙烯纤维断裂强度均符合Weibull分布。
3.3.3 Weibull参数m和σ0
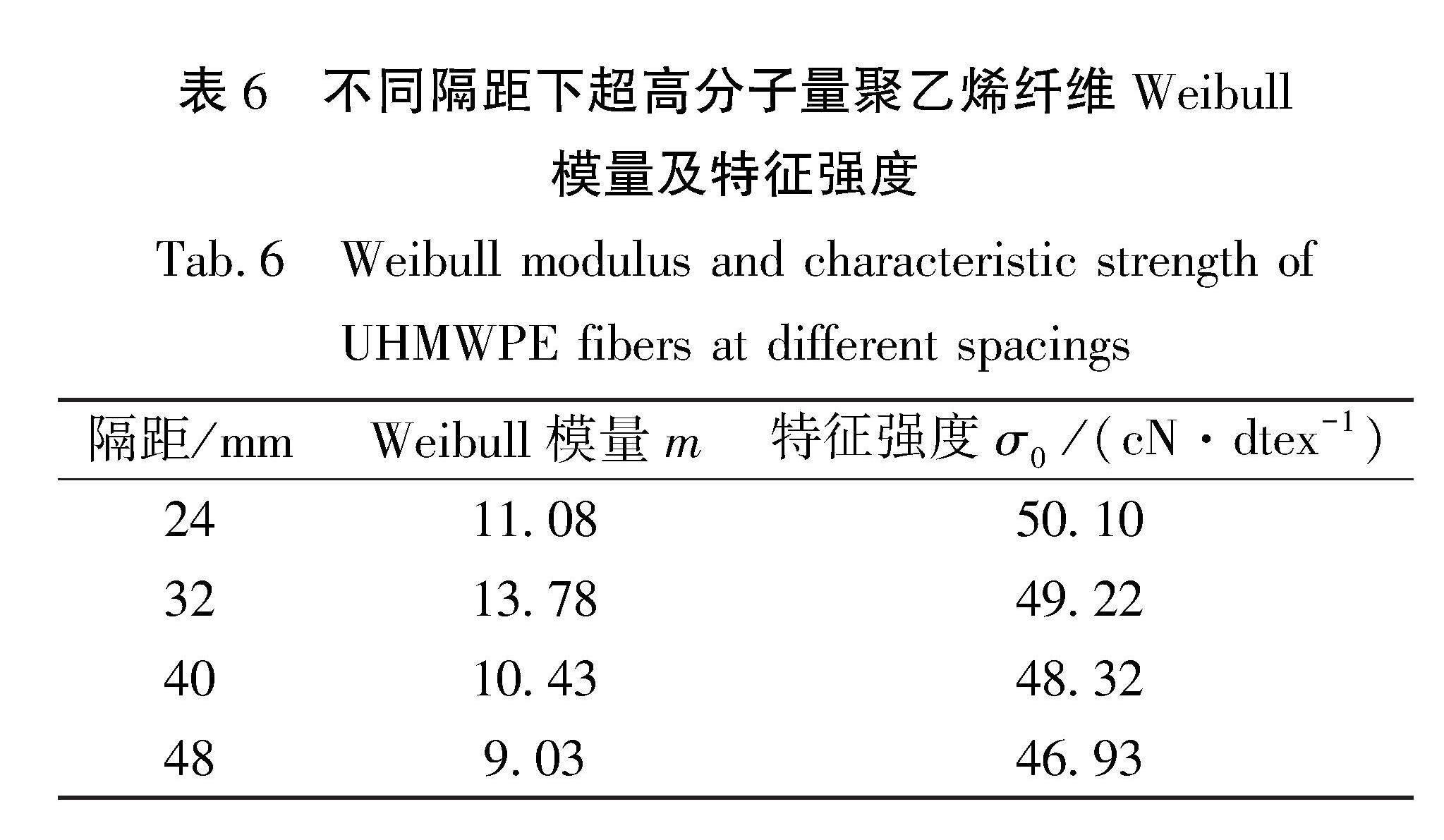
根据图2和式(6),可以得出不同隔距下超高分子量聚乙烯纤维Weibull参数模量以及特征强度如表6所示。
从表6可知,4种隔距的Weibull模量值均不相同,这与随机误差有关。特征强度随着隔距的增大而减小。Xia等 [19]在探究不同隔距下黄麻纤维的特征强度时也得出了类似结论。这是由于测试隔距越大,使纤维发生断裂的弱节出现的概率越大。
3.3.4 Weibull参数γ
纤维变异系数的对数值与纤维测试隔距的对数值呈线性关系,其直线斜率即为Weibull参数γ[15](纤维直径变异值用VFD表示)。图3为纤维直径变异值与测试隔距线性关系图。
如图3所示,线性相关系数R2值为0.903,因此ln(VFD)与ln(L)存在良好的线性关系。可以得出式(16)。
ln(VFD)=0.375×ln(L)-1.064+e(16)
式中e为随机误差。由式(16)可以得出,Weibull参数γ值为0.375。
variation and test spacing
3.4 8.3 tex复丝断裂强度预测
采用Weibull方程进行预测时,被预测隔距距离预测隔距越近,其预测结果越准确[19]。因此选取48 mm作为预测隔距,预测50、200 mm隔距8.3 tex复丝断裂强度。
根据式(11)、(13)、(15)及式(16)得到的γ值以及基于48 mm测试隔距得到的单纤维断裂强力,可以得到50、200 mm隔距两参数和改进Weibull模型对8.3 tex复丝断裂强度预测值以及误差率,如表7和图4所示。
根据图4所示的误差分析可知,两参数Weibull方程预测50、200 mm隔距下8.3 tex复丝断裂强度与其实测值差距较大,预测准确度很低,且均在实测值95%置信区间外,因此两参数Weibull方程无法对50、200 mm隔距8.3 tex复丝断裂强度进行预测。采用改进Weibull方程对其进行预测可得,在50、200 mm隔距下8.3 tex复丝断裂强度预测值的误差率均低于两参数Weibull方程,预测准确度高,且均在其实
测值95%置信区间内,表明改进Weibull方程可以对50、200 mm隔距下8.3 tex复丝断裂强度进行预测。
3.5 单层编织缝线断裂强度预测
根据48 mm测试隔距得到的单纤维断裂强力和纱线表面纤维之间夹角θ为28.79°,通过式(12)、式(14)—(15),可以得到200 mm隔距两参数和改进Weibull模型对单层编织缝线断裂强度预测值以及误差率,如表8和图5所示。
从图5中可以发现,单层编织缝线断裂强度与8.3 tex复丝断裂强度的预测结果相似,两参数Weibull方程的预测值与实测值误差较大,改进Weibull方程的预测值均在其实测值95%置信区间内。表明改进Weibull方程的预测值比两参数Weibull方程的预测值准确度高,改进Weibull方程可以对200 mm隔距单层编织缝线的断裂强度进行预测。
4 结论
本文采用8.3 tex超高分子量聚乙烯纤维为原材料,通过编织工艺完成了高强缝合锚钉缝线的制备,研究其断裂强度;并改进了现有的Weibull模型,提升对其断裂强度预测的准确率。主要研究结论如下:
a)本文制备的单层编织缝线强力为299.8 N,改进后的轴向衬纱双层编织缝线强力高达393.0 N。
b)不论是对8.3 tex复丝断裂强度预测还是对单层编织缝线断裂强度的预测,改进Weibull模型预测值均比两参数Weibull模型预测值准确。
c)采用改进Weibull模型,实现了从单纤维到复丝再到纱线的断裂强度预测。
本文所制备的高强缝合锚钉缝线比同类型医用缝线强力优异,可提高缝合锚钉的机械稳定性,从而为骨科手术减少医疗隐患,为患者提供更好的医疗保障,并为医用缝线结构设计和力学性能分析提供理论依据。
参考文献:
[1]TROFA D P, BIXBY E C, FLEISCHLI J E, et al. All-suture anchors in orthopaedic surgery: Design, rationale, biomechanical data, and clinical outcomes[J]. Journal of the American Academy of Orthopaedic Surgeons, 2021, 29(19): e950-e960.
[2]李海鹏, 辛培源, 朱娟丽, 等.锚钉修复Bankart损伤后关节软骨损伤1例报告[J].中国矫形外科杂志,2023, 31(2): 189-190.
LI Haipeng, XIN Peiyuan, ZHU Juanli, et al. Repair of articular cartilage injury after Bankart injury with anchor nail: A case report[J].Orthopedic Journal of China, 2023, 31(2): 189-190.
[3]余承瑄, 冯思嘉, 王鹏, 等.全缝线锚钉治疗肩关节运动损伤研究进展[J].中国运动医学杂志, 2022, 41(10): 812-821.
YU Chengxuan, FENG Sijia, WANG Peng, et al. Research progress of total suture anchor nail in the treatment of shoulder joint sports injury[J]. Chinese Journal of Sports Medicine, 2022, 41(10): 812-821.
[4]史文骥, 毛宾尧, 汪枫祺, 等.老年肩袖撕裂关节镜下修复方式再探讨[J].中国骨伤, 2021, 34(11): 1040-1043.
SHI Wenji, MAO Binyao, WANG Fengqi, et al. Re-discussion on arthroscopic repair of rotator cuff tear in aged patients[J]. China Journal of Orthopaedics and Traumatology, 2021, 34(11): 1040-1043.
[5]曾斌, 吴旭东, 黄小刚等.关节镜下Healix带线锚钉经胫骨隧道缝合固定治疗半月板撕裂[J].中医正骨, 2021, 33(1):60-62.
ZENG Bin, WU Xudong, HUANG Xiaogang, et al. Arthroscopic internal fixation with Healix suture anchor through tibial tunnel for treatment of meniscus tear[J]. The Journal of Traditional Chinese Orthopedics and Traumatology, 2021, 33(1):60-62.
[6]SMUIN D M, VANNATTA E, AMMERMAN B, et al. Increased load to failure in biceps tenodesis with all-suture suture anchor compared with interference screw: A cadaveric biomechanical study.[J]. Arthroscopy, 2021, 37(10): 3016-3021.
[7]BARBER F A. Regarding "biomechanical analysis of medial-row all-suture suture anchor fixation for rotator cuff repair in a pair-matched cadaveric model"[J]. Arthroscopy: The Journal of Arthroscopic & Related Surgery, 2019, 35(8): 2260-2261.
[8]KHALILI A, KROMP K. Statistical properties of Weibull estimators[J]. Journal of Materials Science, 1991, 26(24): 6741-6752.
[9]NAIK D L, FRONK T H. Weibull distribution analysis of the tensile strength of the kenaf bast fiber[J]. Fibers and Polymers, 2016, 17(10): 1696-1701.
[10]孟志新, 罗磊, 陈婧旖, 等.纤维丝束大小对Mini-C/SiC拉伸性能与强度分布的影响[J].当代化工, 2021, 50(8): 1810-1813.
MENG Zhixin, LUO Lei, CHEN Jingyi, et al. Influence of fiber bundle size on tensile properties and strength distribution of mini-C/SiC[J]. Contemporary Chemical Industry, 2021, 50(8): 1810-1813.
[11]刘家鑫,李秉洋,钟勇, 等.基于声发射技术的T700碳纤维/树脂基体界面性能评估[J].装备环境工程, 2023, 20(5):111-118.
LIU Jiaxin, LI Bingyang, ZHONG Yong, et al. Evaluation of interfacial performance of T700 carbon fiber/resin matrix by acoustic emission [J]. Equipment Environmental Engineering, 2023, 20(5): 111-118.
[12]张晨,孙国栋,雷豹, 等.单向纤维束SIC/SIC复合材料强度统计分布规律与微结构损伤分析[J].复合材料学报, 2023, 40(7):4210-4225.
ZHANG Chen, SUN Guodong, LEI Bao, et al. Statistical distribution pattern of strength and microstructural damage analysis of unidirectional fiber bundle SiC/SiC composites[J]. Acta Materiae Compositae Sinica, 2023, 40(7): 4210-4225.
[13]DEMBRI I, BELAADI A, BOUMAAZA M, et al. Tensile behavior and statistical analysis of Washingtonia filifera fibers as potential reinforcement for industrial polymer biocomposites[J]. Journal of Natural Fibers, 2022, 19(16): 14839-14854.
[14]ZHANG Y P, WANG X G, PAN N, et al. Weibull analysis of the tensile behavior of fibers with geometrical irregularities[J]. Journal of Materials Science, 2002, 37(7): 1401-1406.
[15]XIA Z P, YU J Y, CHENG L D, et al. Study on the breaking strength of jute fibres using modified Weibull distribution[J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(1): 54-59.
[16]LAIFA F, ROKBI M, AMROUNE S, et al. Investigation of mechanical, physicochemical, and thermal properties of new fiber from Silybum marianum bark fiber[J]. Journal of Composite Materials, 2022, 56(14): 2227-2238.
[17]谭燕, 陈兴祥, 肖衡林, 等. 基于三参数Weibull模型的玄武岩再生混凝土疲劳寿命分析[J].中国科技论文, 2022, 17(7):801-806.
TAN Yan, CHEN Xingxiang, XIAO Henglin, et al. Fatigue life analysis of basalt recycled concrete based on three-parameter Weibull model[J]. China Sciencepaper, 2022, 17(7):801-806.
[18]DANIELS H E .The Statistical Theory of the strength of bundles of threads. I[J].Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1945, 183(995): 405-435.
[19]XIA Z P, YU J Y, CHENG L D, et al. Study of the tensile properties of jute/cotton blended yarns using weibull distributions[J]. Research Journal of Textile and Apparel, 2010, 14(1): 18-25.
[20]BARBER F A, HERBERT M A, COONS D A, et al. Sutures and suture anchors: Update 2006[J]. Arthroscopy, 2006, 22(10): 1063-1069.
[21]BARBER F A, HERBERT M A, BEAVIS R C. Cyclic load and failure behavior of arthroscopic knots and high strength sutures[J]. Arthroscopy: The Journal of Arthroscopic & Related Surgery, 2009, 25(2): 192-199.
[22]XIA Z P. Studying the mechanical properties of jute/cotton blended yarns using the weibull model [J]. Journal of Donghua University(English Edition), 2009, 26 (4): 393-396.
Prediction of suture strength of high-strength suture anchors based on
modified Weibull model
LI Xinya1, WANG Ning1, LU Jiahao2, ZHANG Peng3, XIA Zhaopeng1,2, HOU Lei1
(1.School of Textile Science and Engineering, Tiangong University, Tianjin 300387, China;
2.Qinghai Provincial Institute for Product Quality Inspection and Testing, Xining 810000, China;
3.Department of Sports Medicine, Characteristic Medical Center of Chinese
People's Armed Police Forces, Tianjin 300162, China)
Abstract:
Suture anchors play a pivotal role in securely affixing soft tissue to the skeletal framework, having emerged as indispensable tools in the realm of orthopedic surgery. The genesis of suture anchors, comprised initially of metallic screws and sutures, traces back over three decades. In the pursuit of augmenting the tensile strength of these suture anchors, a plethora of variants have been conceived, encompassing metallic suture anchors, biodegradable suture anchors, bio-stable suture anchors, bio-composite suture anchors, and all-suture anchors. The quintessential suture anchor necessitates the provision of substantial mechanical stability to ensure the resolute fixation of soft tissue upon osseous substrates. Within the realm of suture anchors, it is noteworthy that improvements in the anchoring component have mitigated suture rupture as a primary cause of surgical failure in orthopedics. Thus, augmenting suture tensile strength represents the crux of the contemporary challenge. This investigation delves into the fabrication of high-strength suture anchor sutures and scrutinizes their mechanical properties. Leveraging a braiding methodology, we have manufactured high-tensile suture anchor sutures, further prognosticating the rupture strength of suture anchor sutures via both two-parameter Weibull model and modified Weibull model, thereby mitigating risks associated with the utilization of suture anchors.
In this experimental endeavor, 8.3 tex UHMWPE fibers were adopted as the primary raw material, and a braiding technique was employed to engender single-layer braided sutures as well as axially-reinforced double-layer braided sutures. To scrutinize their mechanical properties, we selected varying intervals of 8, 16, 24, 32, 40, and 48 mm to test the tensile strength of individual fibers, opted for 50 and 200 mm intervals for assessing the tensile strength of 8.3 tex filaments, and relied upon a 200 mm interval for gauging the tensile strength of single-layer braided sutures and axially-reinforced double-layer braided sutures. Concurrently, the diameter of fibers and the angular displacement between fibers within the sutures were subjected to meticulous measurement. Subsequently, both the two-parameter Weibull model and the modified Weibull model were employed to characterize the tensile strength of individual fibers, 8.3 tex filament, and single-layer braided sutures.
The findings unveiled that the fracture strength of single-layer braided sutures stood at 299.8 N, whereas axially-reinforced double-layer braided sutures exhibited an impressive fracture strength soaring to 393.0 N. Regrettably, when utilizing the two-parameter Weibull model to prognosticate the rupture strength of 8.3 tex filament and single-layer braided sutures, substantial disparities from actual values were noted, with all predictions falling outside the 95% confidence interval of the observed values and an accuracy rate of less than 5%. Conversely, the forecasts derived from the modified Weibull model consistently fell within the 95% confidence interval of the actual values, attesting to their superior accuracy.
This study's manufactured high-tensile suture anchor sutures evince superior tensile strength when juxtaposed with analogous medical sutures. The axially-reinforced double-layer braided sutures, in particular, attain a formidable rupture strength of 393.0 N. Whether it pertains to the prediction of the tensile strength of 8.3 tex filament or single-layer braided sutures, the modified Weibull model's prognostications surpass the accuracy of those rendered by the two-parameter Weibull model. Furthermore, by employing the modified Weibull model, it becomes possible to predict the tensile strength from individual fibers to filaments and subsequently to yarns. This achievement establishes a solid theoretical foundation for future research in medical suture structural design and mechanical performance analysis.
Keywords:
suture anchor sutures; UHMWPE; fracture strength; two-parameter Weibull model; modified Weibull model; strength prediction
——具有历史感的工具

