有限元分析技术在织物力学性能领域的应用
李登高 刘成霞

DOI: 10.19398/j.att.202310019
摘 要:随着计算机和软件技术的快速发展,有限元分析技术展现出越来越大的潜力,已成为纺织服装领域进行力学性能研究的重要手段。为促进有限元分析技术在织物力学性能中的有效应用,更好地解决生产实践中的问题,首先从实验图像和物理几何手段两方面,阐述了目前织物几何模型的构建方法;梳理了织物材料连续模型、离散模型、半离散模型等本构模型的研究进展;其次,归纳了目前常用有限元分析软件的应用领域及优缺点,概括了有限元技术在织物拉伸、撕裂、防弹冲击、弯曲等力学性能领域的应用现状;最后指出当前研究存在模型精度不足、材料参数难确定、边界条件设置困难等不足,后续可以从应用多尺度分析方法、开发高精纺织检测仪、进行多物理场耦合模拟等方面展开研究。研究结果可用于指导生产实践,更好地解决织物力学性能的相关问题。
关键词:有限元;织物;力学性能;拉伸;防弹;撕裂;弯曲
中图分类号:TS101.8
文献标志码:A
文章编号:1009-265X(2024)06-0129-13
收稿日期:20231023
网络出版日期:20240227
基金项目:国家自然科学基金项目(51405446)
作者简介:李登高(2000—),男,安徽合肥人,硕士研究生,主要从事纺织品性能方面的研究。
通信作者:刘成霞,E-mail:glorior_liu@163.com
最初被用来研究飞机复杂结构的有限元(Finite element,FE)分析技术,是一种将弹性理论、数学和计算机软件有机结合的数值分析技术[1]。由于该分析技术求解精度较高,可摆脱实际物理条件的限制,非常适合表征织物力学性能。20世纪70年代,Lloyd等[2]便将有限元技术用于织物力学结构分析,将织物看作连续介质,采用无弯曲阻力的薄膜单元探究了织物形变。这一时期主要使用简单的平面应力应变模型,忽略织物的三维性质和纤维层次结构,对织物力学行为的描述不够准确。20世纪80年代起,三维模型开始用于织物力学性质的模拟,研究主要集中在结构建模和分析方面,如Imaka等[3]利用三角形有限单元构建了织物三维模型;Zhao等[4]和Tan等[5]设定经纬纱长度及有限单元边长不变,将几何约束条件引入三角形弯曲有限单元。由于不必进行重复实验,有限元模拟技术可以节约大量测试时间和成本,是一种高效的工程分析方法,且随着近年来计算机技术的快速发展,该技术在织物力学性能领域的应用也越来越广泛和深入。
本文通过总结织物有限元模型的构建方法、分析常用有限元分析软件的特点,阐述有限元分析技术在织物拉伸、防弹、撕裂、弯曲等方面的应用现状,指出目前存在的问题及未来的发展方向,以期推动有限元技术在织物力学性能领域的有效应用。
1 织物有限元模型的构建
利用有限元技术分析织物力学性能时,需要根据实际情况选择合适的几何模型、材料本构模型,从而生成有限元模型。
1.1 织物几何模型的生成
1.1.1 基于实验图像的模型生成方法
该方法是利用实验测量的织物结构参数(包括编织结构、纱线截面、纱线间距等)[6],或拍摄的织物图像来创建织物模型,通过指定关键点坐标、周期性条件,选择合适的插值方法在建模软件中生成纱线空间路径[7],再结合实验数据,采用形状函数,再现织物几何形状[8]。如先用正弦曲线生成经纬纱结构,进而构建织物二维几何模型,再利用CAD软件I-DEAS得到织物三维模型[7-8],或直接利用图像构建几何模型[9-11],但此类方法建模过程需要耗费大量人力。
基于图像生成模型的方法可获得精细、真实的织物结构,适合织物局部建模,但建模精度对实验数据的准确性及三维图像质量的依赖性较大,且模型重复利用率较低。
1.1.2 基于物理几何算法的模型生成方法
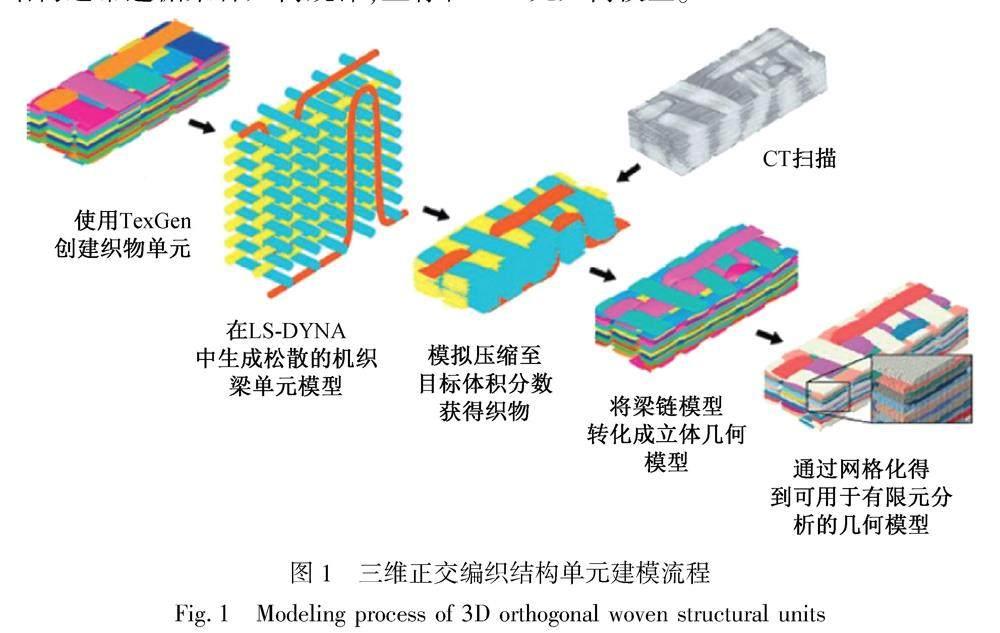
由于织物结构通常遵循某种几何规律,且存在同质性,可利用这些特征简化模型生成过程,并通过本构定律和运动学模型模拟织造过程,从而生成织物模型。如Green等[12]提出了一种基于物理几何算法生成三维正交编织结构单元的建模方法,建模流程如图1所示。先利用TexGen软件生成织物单元,将其导入LS-DYNA软件中生成松散的梁单元机织模型,随后对纱线施加载荷以获得目标体积分数的织物,并通过Python脚本将梁链模型转换成立体几何模型,最后对其立体几何模型网格化,得到有限元几何模型。
还可基于特定的几何规则生成纱线,进而生成不同复杂程度的织物模型。如Kowalczyk等[13]利用正弦曲线构建了平纹织物几何模型,将纱线中心轴假设为正弦曲线,纱线围绕该正弦曲线自由成形,且波动仅受相邻纱线影响,该方法建模时必须考虑纱线的截面变化和相互重叠情况,目前的解决方法是通过控制样条点来调节纱线截面[14-16],如通过利用Catmull-Rom样条线和样条点,可以构造出不同组织结构的机织物和针织物模型[17]。
与基于实验数据生成模型的方法相比,利用物理几何算法生成模型的方法无需测量实际织物尺寸,生成的织物模型也更易构建周期性边界条件,适用于结构及尺寸较大的织物。
1.2 织物材料的本构模型
用于表示材料力学特性的本构模型可分为3类:连续模型、离散模型和半离散模型。
1.2.1 连续模型
当织物被假设为连续均匀介质时,可以使用非正交弹性、亚弹性、超弹性、耗散等模型来描述其力学特性,如图2所示。其中Peng等[18]提出可用来表征机织复合材料大变形条件下各向异性的非正交弹性本构模型
,如图2(a)所示,通过在壳单元中嵌入对称轴坐标系,将本构关系中的反变应力分量和协变应变分量引入该坐标系中,利用连续介质力学理论构建机织复合材料纤维取向模型。亚弹性本构模型可用来分析织物的大应变力学行为,如图2(b)所示,已被嵌入ABAQUS软件中[19]。
超弹性模型是基于能量密度函数的本构模型,可用来描述织物在形变过程中储存和释放的能量,适用于分析高弹织物的大形变行为[20]。Yang等[21]利用网状纤维橡胶复合材料的超粘弹本构模型,研究了温度对织物密封件力学性能的影响。此外,Xu等[22]在Yang的基础上,利用超弹性模型预测了复合材料织物不同方向的应力-应变行为。超弹性模型还可用于预测复合材料织物悬垂性等复杂形变[23],如图2(c)所示,以及用于表征平纹织物的非线性各向异性[24],其优点是能同时考虑织物双轴拉伸引起的耦合效应,以及经、纬纱相对旋转引起的剪切能。由于弹性或超弹性模型不能描述织物塑性变形和纱线摩擦引起的能量耗散[25],Denis等[26]提出了能量耗散模型,如图2(d)所示,研究发现纤维摩擦导致的能量耗散仅与面内剪切变形有关[27]。
连续介质有限元模型可以在宏观尺度上快速有效地模拟织物的复杂力学行为,无需考虑织物的细观结构和微观组分,易于在现有的商业软件中实现,但不能反映织物内部纤维束的交织、滑移、扭转和变形等细观变化。
1.2.2 离散模型
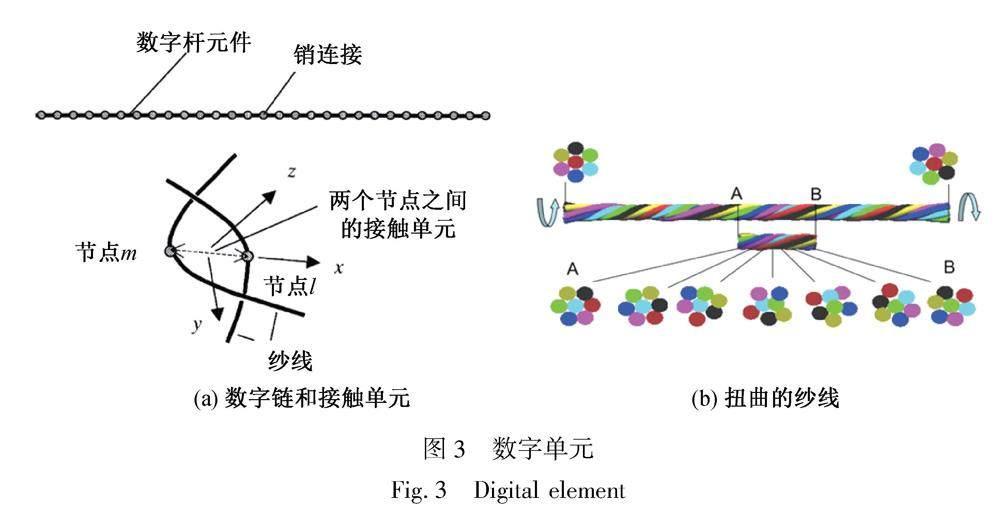
与连续介质模型相比,离散模型可描述中观尺度(纱线水平)或微观尺度(纤维水平)的织物,如其中的数字单元模型[28-29],如图3所示,可用于模拟纺织过程及织物微观几何结构,每根纤维被模拟成一个无摩擦的销连接杆元链,即“数字链”,该数字单元不可延伸,没有弯曲刚度,其元素长度接近零,如图3(a)所示,数字链之间由接触元件相连,图3(b)展示了微观纱线模型的扭曲效果。
Wang等[28]在数字单元基础上,提出了微观尺度的虚拟纤维概念,通过连接三维桁架或梁单元生成虚拟纤维,进而对非卷曲织物[30]、二维织物层[31]、纬编针织物[32]、三维机织[33-34]等进行建模。但当织物的机械响应由纤维弯曲引起时,建模精度会受限,且不能同时表征长丝的高拉伸和低弯曲刚度。针对这一问题,Daelemans等[35]通过网格重叠技术,分别利用桁架和梁单元,即混合建模法,来模拟纤维的拉伸与弯曲过程,结果表明混合建模法可以很好地模拟织物的宏观压缩响应。由于纱线中包含的纤维成千上万,构建微观尺度的离散模型计算量巨大,因此目前微观尺度的离散模型仅用于小范围分析。
为减少计算量,还可采用纱线级的离散模型[36-37],通过多尺度建模方法,构建纱线加纱线、纤维加纱线和纤维加壳等模型来模拟织物[38]。与微观尺度的纤维模型相比,中观尺度的纱线模型计算效率会显著提高,但纱线属性的确定要依赖实验测试,且不能精确再现纱线接触区域的复杂几何形状,也难以表征纱线间的摩擦作用。
1.2.3 半离散模型
半离散模型[39-41]由一组离散的织物单元格组成,是连续模型和离散模型的综合,图4展示了由织物单元格构成的半离散模型[40] ,以及半离散模型的弯曲和扭转复形状态[42]。通过半离散模型可获得织物的细观结构,由于其组成单元数量远少于离散模型,计算效率也比离散模型高。与连续模型相比,半离散模型不使用应力张量,直接定义经纬纱张力及面内剪切和弯曲力矩[43],利用半离散模型可以模拟织物的预成形能力[44]。在此基础上,Guan等[42]进一步考虑织物横向压缩、面内剪切和弯曲性,构建了半离散2.5维模型,并将其嵌入Abaqus/ Explicit中,用于模拟机织物的成形过程。
1.3 有限元模型的生成
有限元软件中的模型可分为实体模型、桁架、梁、壳单元和混合单元模型[45]。实体模型用三维实体单元表示织物结构,是目前应用最广的形式。壳单元模型将织物简化为薄层结构,可以减少计算量和存储量,适用于织物静态力学性能的分析。桁架、梁模型分别将织物视为由线性弹性杆件或梁组成的空间框架结构,可模拟织物的纤维结构。混合单元模型则将织物视为由不同单元组成的混合结构,可表征织物多种力学性能,但需要处理不同单元之间的连接和耦合问题。
建立织物几何结构后,需通过网格生成将织物的几何结构离散成数量有限的单元,常用的网格包括自适应网格和规则网格[46]。织物力学建模时通常采用前者,生成自适应网格时需选取合适的节点和单元个数,以实现计算精度和效率的平衡,图5分别展示了针织线圈在不同网格密度下的划分结果[47],网格划分越密,计算结果越精确,但运算时间也越长。除网格外,模型生成时选择的单元也不尽相同,常用的单元包括六面体和四面体等,每个小单元可用节点来描述。完成上述设置后,根据研究需求选择合适的材料本构模型,与有限元网格相耦合就可得到织物有限元模型。
2 常用的有限元分析技术软件
利用有限元技术分析织物力学、热学、电学等性能时,常需要借助一些软件,常见的有限元分析软件如表1所示。
3 有限元分析技术在织物力学领域的应用现状
有限元技术可用于模拟和分析织物力学、热学、电学、流体动力学等多种行为,尤其适合且能全面描述织物力学性能,以下将从拉伸、防弹、撕裂、弯曲4个方面进行介绍。
3.1 拉伸性能
按受力方向的不同,拉伸可分为:(a)沿经向或纬向的单轴向拉伸,如弹性变形和塑性变形;(b)沿经、纬方向同时作用的双轴拉伸,考虑两个方向的变形和强度,更能反映材料的各向异性[50];(c)沿与材料有一定角度的方向施加拉力的离轴拉伸,可直接或间接得到材料的模量、强度等参数[51]。目前在织物拉伸领域的研究主要集中在纱线层面,如表2所示。
3.2 防弹性能
防弹性能是指织物抵抗高速飞行物体穿透和冲击破坏的能力,有限元技术可以有效分析织物被冲击破坏的过程。按精细程度目前的织物有限元冲击模型分为二维宏观[64] 、纤维级[65] 、纱线级[66]3类,如图6所示。从图6中可以看出,不同的织物冲击模型展现的细节不同。早期的二维织物冲击模型将纱线认为是线弹性材料[67],忽略纱线间的摩擦,后续研究[65]表明摩擦在织物防弹冲击中起重要作用,用数字单元建立的纤维级微观织物模型,可更详细地展示弹体穿透织物时的摩擦及损伤过程[68],但计算耗时大,成本高。纱线级模型则能综合两者优点,具备一定精度的同时,降低分析成本。出于这一考虑,诞生了多尺度模型[69],即用宏观连续模型替代远离弹道冲击的区域,但多尺度模型中的简化结构难以解释纱线的断裂、卷曲、滑移等。对此,Meyer等[66]分别建立了宏观连续及中尺度有限元模型,来研究织物的冲击响应过程。
近期对弹道冲击模拟的研究主要在纱线层面展开[70],如模拟三维正交机织物在弹丸冲击下的渐进破坏过程,及初始速度对球形弹体破坏形态的影响[71];并将多尺度织物模型用于研究射弹形状及射击速度对织物破坏形式的影响[72]。
3.3 撕裂性能
撕裂是以预切口为扩展起点的织物破坏形式,也是导致织物失效或寿命终止的常见方式[73-75],研究撕裂性能对提高织物耐用性有重要
作用,织物撕裂常用的试验方法包括舌形试样法、梯形试样法等,二者的纱线级模型如图7所示,图7(a)中的模型可用于探究经纬密度对织物撕裂强力的影响[73],也能揭示撕裂三角区的破坏形态,图7(b)中的模型则可模拟斜纹织物的动态撕裂过程[75]。目前织物撕裂性能的有限元模拟研究还不够深入[76],接下来需要构建纤维级织物撕裂形式的有限元模型,以实现对这一破坏形式的进一步剖析。
3.4 弯曲性能
弯曲性是织物抵抗弯曲形变的能力,与织物的悬垂性、抗皱性等密切相关,可通过斜面法、纯弯曲法、三点梁弯曲法等来测试,也可借助有限元技术对其进行模拟和表征。Senner等[77]应用分析梁理论,校准了表征单向非卷曲织物弯曲行为的本构模型。靳欢欢等[78]利用显微镜获取的织物图像参数,构建了纱线级连续实体模型,对机织物的3点梁弯曲性进行了模拟与分析。此外ABAQUS软件中的单胞有限元模型通过对约束方程的逐点施加,可准确预测复合材料织物的弯曲刚度[79],而天然纤维复合材料的峰值抗弯载荷和损伤模式则可通过多尺度有限元模型进行预测[80]。虽然目前利用有限元技术可获得织物弯曲刚度、弯曲力矩等,但由于计算量庞大,模型还不够精确,难以模拟弯曲过程中纱线内部纤维的抱合状态,弯曲测试过程也缺乏统一的标准。
4 研究不足和后续发展方向
4.1 研究不足
在织物力学性能模拟中,有限元技术虽然起到了重要作用,但也存在一些不足,主要有以下几个方面:
a)模型精度不够。精细的模型对计算机性能有较高要求,故有限元模型建立时,常需要对模型进行各种假设,如忽略织物的非线性、各向异性等,这些假设会影响模型精度。此外目前应用最广的中观有限元模型,即纱线级模型,可较真实地刻画纱线结构、局部应力、应变,以及任意时刻下不同部位的受力状态[81-82],但无法模拟实际织物或纱线中成千上万纤维的形态、受力等,从而影响模拟结果的准确性。
b)材料参数难确定。纱线是由纤维组成的集合体,纤维之间存在相对滑动,织物材料特性往往受纤维类型、排布方式、纤维间作用力等因素影响,但由于这些参数难以确定,为方便模拟,属性设置时常忽略形变时引起的纱线截面变化,以及纱线中纤维间的作用力,这些简化处理难免影响有限元模拟结果的准确性。
c)边界条件处理困难。有限元模型在求解过程中需设定边界条件,如织物的支撑和夹持方式等,但复杂的织物边界条件设置较困难,致使有限元模拟难以精确体现实际织物所处状态,从而影响模拟结果的准确性。
4.2 后续发展方向
4.2.1 应用多尺度分析方法
多尺度分析方法可将不同尺度的几何特征、应力应变场状态和损伤信息联系起来,并兼顾计算效率和局部细节。因此将来研究的重点是建立高保真的几何模型,反映织物内部结构和缺陷特征,为高精度的有限元模型建立提供基础。并在确定多尺度分析适用范围基础上,开发高效的多尺度分析算法,实现不同尺度织物模型的协调求解,保留织物关键力学特征的同时减少计算成本。
4.2.2 开发高精纺织检测仪
建立有限元模型时通常进行步骤简化和条件假设,如忽略纱线间差异,不考虑纤维层面的变化及纱线截面的形变,假设纱线表面均匀且平滑等,究其原因是这些参数难以测量,这些假设提高模拟效率的同时,也极大地影响了模拟结果的准确性。后续研究可以结合图像及信号处理技术、高精度传感器技术等,开发纱线截面及摩擦性检测仪,以及纤维弯曲性、摩擦性检测仪等,利用这些精密仪器的实验结果,验证有限元分析结果的准确性,拓展有限元分析技术的应用领域。
4.2.3 进行多物理场耦合模拟
利用有限元技术进行力学分析时通常仅考虑织物本身,将环境视作真空,如研究织物导热性、吸湿性时都是单物理场分析,但实际上织物几何形态、材料特性会受所处环境的综合影响,如热传递、流体、电磁等都会改变织物性能。另外织物也常与金属、陶瓷、塑料等材料复合,从而影响整体的力学性能。在后续有限元分析时,可考虑织物多物理场行为,即利用有限元技术研究温度、湿度、压强等对织物力学性能的综合影响。
4.2.4 与其他数值方法相结合
有限元分析技术虽然可以解决许多复杂的力学问题,但也有一些局限和不足,如网格依赖性大、收敛性与稳定性要求高等。因此,可以结合其他数值方法,如边界元法、有限差分法、机器学习等,通过优势互补,强强联手,实现对复杂问题的高效求解,来克服有限元分析技术的缺陷,并提高其精度。
参考文献:
[1]LOMOV S V, IVANOV D S, VERPOEST I, et al. Meso-FE modelling of textile composites: Road map, data flow and algorithms[J]. Composites Science and Technology, 2007, 67(9): 1870-1891.
[2]LLOYD D W. The Analysis of Complex Fabric Defor-mations[M]//Mechanics of Flexible Fibre Assemblies. Dordrecht: Springer Netherlands, 1980: 311-342.
[3]IMAKA H, OKABE H, NISHIKAWA S, et al. A method of estimating the three-dimensional shapes of garments by use of triangular finite elements[J]. Bulletin of Research Institute for Polymers and Textiles, 1984: 73-80.
[4]ZHAO Y F, WONG T N, TAN S T, et al. A model for simulating flexible surfaces of cloth objects[J]. Computers & Structures, 1997, 63(1): 133-147.
[5]TAN S T, WONG T N, ZHAO Y F, et al. A constrained finite element method for modeling cloth deformation[J]. The Visual Computer, 1999, 15(2): 90-99.
[6]JACQUES S, DE B I, VAN P W. Application of periodic boundary conditions on multiple part finite element meshes for the meso-scale homogenization of textile fabric composites[J]. Composites Science and Technology, 2014, 92: 41-54.
[7]WIJAYA W, KELLY P A, BICKERTON S. A novel methodology to construct periodic multi-layer 2D woven unit cells with random nesting configurations directly from μCT-scans[J]. Composites Science and Technology, 2020, 193: 108125.
[8]SEVENOIS R D B, GAROZ D, GILABERT F A, et al. Avoiding interpenetrations and the importance of nesting in analytic geometry construction for Representative Unit Cells of woven composite laminates[J]. Composites Science and Technology, 2016, 136: 119-132.
[9]BARBERO E J, DAMIANI T M, TROVILLION J. Micromechanics of fabric reinforced composites with periodic microstructure[J]. International Journal of Solids and Structures, 2005, 42(9/10): 2489-2504.
[10]BARBERO E J, TROVILLION J, MAYUGO J A, et al. Finite element modeling of plain weave fabrics from photomicrograph measurements[J]. Composite Structures, 2006, 73(1): 41-52.
[11]杨斌, 王继辉, 冯雨薇, 等. 织物增强复合材料Micro-CT辅助数值仿真技术研究进展[J]. 复合材料学报, 2023, 40(10): 5466-5485.
YANG Bin, WANG Jihui, FENG Yuwei, et al. Advances in Micro-CT aided numerical simulation of fabric-reinforced composites[J]. Acta Materiae Compositae Sinica, 2023, 40(10): 5466-5485.
[12]GREEN S D, LONG A C, EL S B, et al. Numerical modelling of 3D woven preform deformations[J]. Composite Structures, 2014, 108: 747-756.
[13]KOWALCZYK P. Enhanced geometric model for numerical microstructure analysis of plain-weave fabric-reinforced composite[J]. Advanced Composite Materials, 2015, 24(5): 411-429.
[14]HIVET G, BOISSE P. Consistent 3D geometrical model of fabric elementary cell. Application to a meshing preprocessor for 3D finite element analysis[J]. Finite Elements in Analysis and Design, 2005, 42(1): 25-49.
[15]ADUMITROAIE A, BARBERO E J. Beyond plain weave fabrics-I. Geometrical model[J]. Composite Structures, 2011, 93(5): 1424-1432.
[16]STIG F, HALLSTRM S. Spatial modelling of 3D-woven textiles[J]. Composite Structures, 2012, 94(5): 1495-1502.
[17]WADEKAR P, PERUMAL V, DION G, et al. An optimized yarn-level geometric model for Finite Element Analysis of weft-knitted fabrics[J]. Computer Aided Geometric Design, 2020, 80: 101883.
[18]PENG X Q, CAO J. A continuum mechanics-based non-orthogonal constitutive model for woven composite fabrics[J]. Composites Part A: Applied Science and Manu-facturing, 2005, 36(6): 859-874.
[19]CHEN B, COLMARS J, NAOUAR N, et al. A hypoelastic stress resultant shell approach for simulations of textile composite reinforcement forming[J]. Composites Part A: Applied Science and Manufacturing, 2021, 149: 106558.
[20]YANG H, YAO X F, YAN H, et al. Anisotropic hyper-viscoelastic behaviors of fabric reinforced rubber composites[J]. Composite Structures, 2018, 187: 116-121.
[21]YANG H, YAO X F, KE Y C, et al. Constitutive behaviors and mechanical characterizations of fabric reinforced rubber composites[J]. Composite Structures, 2016, 152: 117-123.
[22]XU X, YAO X, DONG Y, et al. Mechanical behaviors of non-orthogonal fabric rubber seal[J]. Composite Structures, 2021, 259: 113453.
[23]PAZMINO J, MATHIEU S, CARVELLI V, et al. Numerical modelling of forming of a non-crimp 3D orthogonal weave E-glass composite reinforcement[J]. Composites Part A: Applied Science and Manufacturing, 2015, 72: 207-218.
[24]YAO Y, HUANG X, PENG X, et al. An anisotropic hyperelastic constitutive model for plain weave fabric considering biaxial tension coupling[J]. Textile Research Journal, 2019, 89(3): 434-444.
[25]CAO J, AKKERMAN R, BOISSE P, et al. Characterization of mechanical behavior of woven fabrics: Experimental methods and benchmark results[J]. Composites Part A: Applied Science and Manufacturing, 2008, 39(6): 1037-1053.
[26]DENIS Y, HAMILA N, ITSKOV M, et al. A dissipative model for deep-drawing simulations: Elastic springback prediction and incremental forming strategies[J]. Composites Part A: Applied Science and Manufacturing, 2021, 149: 106547.
[27]DENIS Y, GUZMAN-MALDONADO E, HAMILA N, et al. A dissipative constitutive model for woven composite fabric under large strain[J]. Composites Part A: Applied Science and Manufacturing, 2018, 105: 165-179.
[28]WANG Y, SUN X. Digital-element simulation of textile processes[J]. Composites Science and Technology, 2001, 61(2): 311-319.
[29]WANG Y, MIAO Y, SWENSON D, et al. Digital element approach for simulating impact and penetration of textiles[J]. International Journal of Impact Engineering, 2010, 37(5): 552-560.
[30]THOMPSON A J, EL SAID B, BELNOUE J P H, et al. Modelling process induced deformations in 0/90 non-crimp fabrics at the meso-scale[J]. Composites Science and Technology, 2018, 168: 104-110.
[31]LIU C, XIE J, SUN Y, et al. Micro-scale modeling of textile composites based on the virtual fiber embedded models[J]. Composite Structures, 2019, 230: 111552.
[32]WU L, ZHAO F, XIE J, et al. The deformation behaviors and mechanism of weft knitted fabric based on micro-scale virtual fiber model[J]. International Journal of Mechanical Sciences, 2020, 187: 105929.
[33]MAZUMDER A, WANG Y, YEN C F. A structured method to generate conformal FE mesh for realistic textile composite micro-geometry[J]. Composite Structures, 2020, 239: 112032.
[34]YANG Z, JIAO Y, XIE J, et al. Modeling of 3D woven fibre structures by numerical simulation of the weaving process[J]. Composites Science and Technology, 2021, 206: 108679.
[35]DAELEMANS L, TOMME B, CAGLAR B, et al. Kinematic and mechanical response of dry woven fabrics in through-thickness compression: Virtual fiber modeling with mesh overlay technique and experimental validation[J]. Composites Science and Technology, 2021, 207: 108706.
[36]NILAKANTAN G, KEEFE M, WETZEL E D, et al. Effect of statistical yarn tensile strength on the probabilistic impact response of woven fabrics[J]. Composites Science and Technology, 2012, 72(2): 320-329.
[37]NGUYEN Q T, VIDAL-SALL E, BOISSE P, et al. Mesoscopic scale analyses of textile composite reinforcement compaction[J]. Composites Part B: Engineering, 2013, 44(1): 231-241.
[38]YANG Y, LIU Y, XUE S, et al. Multi-scale finite element modeling of ballistic impact onto woven fabric involving fiber bundles[J]. Composite Structures, 2021, 267: 113856.
[39]HAMILA N, BOISSE P, SABOURIN F, et al. A semi-discrete shell finite element for textile composite reinforcement forming simulation[J]. International Journal for Numerical Methods in Engineering, 2009, 79(12): 1443-1466.
[40]ALLAOUI S, BOISSE P, CHATEL S, et al. Experimental and numerical analyses of textile reinforcement forming of a tetrahedral shape[J]. Composites Part A: Applied Science and Manufacturing, 2011, 42(6): 612-622.
[41]BOISSE P, HAMILA N, VIDAL-SALL E, et al. Simulation of wrinkling during textile composite reinforcement forming. Influence of tensile, in-plane shear and bending stiffnesses[J]. Composites Science and Technology, 2011, 71(5): 683-692.
[42]GUAN W, DAI Y, LI W, et al. An improved semi-discrete approach for simulation of 2.5D woven fabric preforming[J]. Composite Structures, 2022, 282: 115093.
[43]WANG P, LEGRAND X, BOISSE P, et al. Experimental and numerical analyses of manufacturing process of a composite square box part: Comparison between textile reinforcement forming and surface 3D weaving[J]. Composites Part B: Engineering, 2015, 78: 26-34.
[44]DE LUYCKER E, MORESTIN F, BOISSE P, et al. Simulation of 3D interlock composite preforming[J]. Composite Structures, 2009, 88(4): 615-623.
[45]IWATA A, INOUE T, NAOUAR N, et al. Coupled meso-macro simulation of woven fabric local deformation during draping[J]. Composites Part A: Applied Science and Manufacturing, 2019, 118: 267-280.
[46]喻高远, 李俊杰, 楼云锋, 等. 结构动力学有限元混合分层并行计算方法[J]. 工程力学, 2023, 40: 1-8.
YU Gaoyuan, LI Junjie, LOU Yunfeng, et al. Hybrid hierarchical parallel algorithms for structure. dynamic analysis[J]. Engineering Mechanics, 2023, 40: 1-8.
[47]DINH T D, WEEGER O, KAIJIMA S, et al. Prediction of mechanical properties of knitted fabrics under tensile and shear loading: Mesoscale analysis using representative unit cells and its validation[J]. Composites Part B: Engineering, 2018, 148: 81-92.
[48]QUYEN N T, QUOC N T, TRU N D, et al. An alpha finite element method for linear static and buckling analysis of textile-like sheet materials[J]. Solid State Phenomena, 2022, 333: 211-217.
[49]ONYIBO E C, SAFAEI B. Application of finite element analysis to honeycomb sandwich structures: A review[J]. Reports in Mechanical Engineering, 2022, 3(1): 283-300.
[50]顾伯洪.非织造布拉伸性能有限元模拟计算[J].纺织学报,1998,19(3):140-142.
GU Baihong. Finite element simulation calculation of nonwoven tensile propery[J]. Journal of Textile Research, 1998, 19(3): 140-142.
[51]DAELEMANS L, FAES J, ALLAOUI S, et al. Finite element simulation of the woven geometry and mechanical behaviour of a 3D woven dry fabric under tensile and shear loading using the digital element method[J]. Composites Science and Technology, 2016, 137: 177-187.
[52]程建芳, 肖露, 柴晓明, 等. 有限元分析法研究Kevlar129纱线及织物的拉伸性能[J]. 浙江理工大学学报, 2013, 30(5): 649-653.
CHENG Jianfang, XIAO Lu, CHAI Xiaoming, et al. Study on tensile property of Kevlar129 yarn and fabric with finite element analysis method[J]. Journal of Zhejiang Sci-Tech University, 2013, 30(5): 649-653.
[53]李瑛慧, 谢春萍, 刘新金. 三原组织织物拉伸力学性能有限元仿真[J]. 纺织学报, 2017, 38(11): 41-47.
LI Yinghui, XIE Chunping, LIU Xinjin. Finite element simulation on tensile mechanical properties of three-elementary weave fabric[J]. Journal of Textile Research, 2017, 38(11): 41-47.
[54]李瑛慧, 谢春萍, 刘新金, 等. 真丝和涤纶仿真丝织物的拉伸性能有限元仿真[J]. 丝绸, 2018, 55(3): 27-31.
LI Yinghui, XIE Chunping, LIU Xinjin, et al. Finite element simulation of tensile mechanical properties of silk fabrics and polyester silk-like fabrics[J]. Journal of Silk, 2018, 55(3): 27-31.
[55]刘倩楠, 张涵, 刘新金, 等. 基于ABAQUS的三原组织机织物拉伸力学性能模拟[J]. 纺织学报, 2019, 40(4): 44-50.
LIU Qiannan, ZHANG Han, LIU Xinjin, et al. Simulation on tensile mechanical properties of three-elementary weave woven fabrics based on ABAQUS[J]. Journal of Textile Research, 2019, 40(4): 44-50.
[56]刘倩楠, 刘新金. 采用ABAQUS的粘胶机织物拉伸力学性能仿真[J]. 纺织学报, 2018, 39(9): 39-43.
LIU Qiannan, LIU Xinjin. Tensile mechanical properties simulation of viscose woven fabrics based on ABAQUS[J]. Journal of Textile Research, 2018, 39(9): 39-43.
[57]刘倩楠, 刘新金, 苏旭中. 基于有限元方法的不同集聚纱织物拉伸力学性能分析[J].丝绸, 2019, 56(4): 24-29.
LIU Qiannan, LIU Xinjin, SU Xuzhong. Tensile mechanical properties analysis of fabrics with different aggregate yarns based on finite element method[J]. Journal of Silk, 2019,56(4): 24-29.
[58]孙一万, 张学文, 蔡利海, 等. 增强机织物拉伸过程中的应力集中有限元分析[J].复合材料科学与工程, 2021(12): 25-33.
SUN Yiwan, ZHANG Xuewen, CAI Lihai, et al. Finite element analysis of stress concentration in tensile process of reinforced woven fabric[J]. Composites Science and Engineering, 2021(12): 25-33.
[59]孙亚博, 李立军, 马崇启, 等. 基于ABAQUS的筒状纬编针织物拉伸力学性能模拟[J].纺织学报, 2021, 42(2): 107-112.
SUN Yabo, LI Lijun, MA Chongqi, et al. Simulation on tensile properties of tubular weft knitted fabrics based on ABAQUS[J]. Journal of Textile Research,2021, 42(2): 107-112.
[60]HOU Y, JIANG L, SUN B, et al. Strain rate effects of tensile behaviors of 3-D orthogonal woven fabric: Experimental and finite element analyses[J]. Textile Research Journal, 2013, 83(4): 337-354.
[61]SU X, LIU X. Dynamic tensile process of blended fabric using finite element method[J]. International Journal of Clothing Science and Technology, 2020, 32(5): 707-724.
[62]GHORBANI E, HASANI H, JAFARI N R. Finite element modelling the mechanical performance of pressure garments produced from elastic weft knitted fabrics[J]. The Journal of The Textile Institute, 2019, 110(5): 724-731.
[63]LIU G, HUANG K, ZHONG Y, et al. Investigation on the off-axis tensile failure behaviors of 3D woven composites through a coupled numerical-experimental approach[J]. Thin-Walled Structures, 2023, 192: 111176.
[64]CHOCRON S, FIGUEROA E, KING N, et al. Modeling and validation of full fabric targets under ballistic impact[J]. Composites Science and Technology, 2010, 70(13): 2012-2022.
[65]DAS S, JAGAN S, SHAW A, et al. Determination of inter-yarn friction and its effect on ballistic response of para-aramid woven fabric under low velocity impact[J]. Composite Structures, 2015, 120: 129-140.
[66]MEYER C S, O'BRIEN D J, HAQUE B Z G, et al. Mesoscale modeling of ballistic impact experiments on a single layer of plain weave composite [J]. Composites Part B: Engineering, 2022, 235: 109-753.
[67]MAMIVAND M, LIAGHAT G H. A model for ballistic impact on multi-layer fabric targets[J]. International Journal of Impact Engineering, 2010, 37(7): 806-812.
[68]WANG Y, MIAO Y, HUANG L, et al. Effect of the inter-fiber friction on fiber damage propagation and ballistic limit of 2-D woven fabrics under a fully confined boundary condition[J]. International Journal of Impact Engineering, 2016, 97: 66-78.
[69]PALTA E, FANG H. On a multi-scale finite element model for evaluating ballistic performance of multi-ply woven fabrics[J]. Composite Structures, 2019, 207: 488-508.
[70]武鲜艳, 申屠宝卿, 马倩, 等. 球形弹体冲击下三维正交机织物结构破坏机制有限元分析[J].纺织学报, 2020, 41(8): 32-38.
WU Xianyan, SHENTU Baoqing, MA Qian, et al. Finite element analysis on structural failure mechanism of three-dimensional orthogonal woven fabrics subjected to impact of spherical projectile[J]. Journal of Textile Research, 2020, 41(8): 32-38.
[71]WEI Q, YANG D, GU B, et al. Numerical and experimental investigation on 3D angle interlock woven fabric under ballistic impact[J]. Composite Structures, 2021, 266: 113778.
[72]DEWANGAN M K, PANIGRAHI S K. Finite element analysis of projectile nose shapes in ballistic perforation of 2D plain woven Kevlar/epoxy composites using multi-scale modelling[J]. Journal of Industrial Textiles, 2022, 51(S3): 4200-4230.
[73]马倩, 王可. 机织物撕裂破坏的有限元模拟[J]. 合成纤维, 2013, 42(5): 10-13.
MA Qian, WANG Ke. Finite element modeling of woven fabric tearing damage[J]. Synthetic Fiber in China, 2013 (5): 10-13.
[74]WANG P, SUN B, GU B. Comparisons of trapezoid tearing behaviors of uncoated and coated woven fabrics from experimental and finite element analysis[J]. International Journal of Damage Mechanics, 2013, 22(4): 464-489.
[75]WANG P, SUN B Z. Finite element analysis and calculation of tongue-tearing process of woven fabric[J]. Advanced Materials Research, 2011, 181/182: 443-448.
[76]ZHOU H, JIANG W, ZHOU B I, et al. Numerical simulation and experimental validation of triaxial woven fabric and its reinforced rubber composites on tear damage[J]. Materials Research Express, 2021, 8(8): 085301.
[77]SENNER T, KREISSL S, MERKLEIN M, et al. Bending of unidirectional non-crimp-fabrics: Experimental characterization, constitutive modeling and application in finite element simulation[J]. Production Engineering, 2015, 9(1): 1-10.
[78]靳欢欢, 杜赵群. 平纹织物三点梁弯曲有限元模拟与分析[J]. 东华大学学报(自然科学版), 2016, 42(3): 344-349.
JIN Huanhuan, DU Zhaoqun. Three-point bending simulation and analysis of plain woven fabric by finite element method[J]. Journal of Donghua University(Natural Science), 2016, 42(3): 344-349.
[79]杨留义, 谭惠丰, 曹宗胜. 基于单胞有限元模型的织物复合材料弯曲刚度预报[J]. 复合材料学报, 2018, 35(5): 1192-1202.
YANG Liuyi, TAN Huifeng, CAO Zongsheng. A unit-cell model for predicting bending stiffnesses of plain woven composites[J]. Acta Materiae Compositae Sinica, 2018, 35(5): 1192-1202.
[80]ZHONG Y, TRAN L Q N, KUREEMUN U, et al. Prediction of the mechanical behavior of flax polypropylene composites based on multi-scale finite element analysis[J]. Journal of Materials Science, 2017, 52(9): 4957-4967.
[81]马莹, 何田田, 陈翔, 等. 基于数字单元法的三维正交织物微观几何结构建模[J]. 纺织学报, 2020, 41(7): 59-66.
MA Ying, HE Tiantian, CHEN Xiang, et al. Micro-geometry modeling of three-dimensional orthogonal woven fabrics based on digital element approach[J]. Journal of Textile Research, 2020, 41(7): 59-66.
[82]DRACH A, DRACH B, TSUKROV I. Processing of fiber architecture data for finite element modeling of 3D woven composites[J]. Advances in Engineering Software, 2014, 72: 18-27.
Application of finite element analysis technology in the field of
fabric mechanical properties
LI Denggaoa, LIU Chengxiaa,b
(a. School of Fashion Design & Engineering; b. Zhejiang Provincial Engineering Laboratory of Fashion
Digital Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)
Abstract:
The mechanical properties of fabrics have always been an important research content in the field of textiles and clothing, but the three-dimensional structure of fabrics is complex, and many factors such as fiber, yarn, weave structure and composite materials will affect the mechanical properties of fabrics. The traditional mechanical experimental methods are often costly, and it is difficult for researchers to observe the changes at the meso level. With the rapid development of computer and software technology, the finite element analysis technology shows more and more potential, and has become an important means of mechanical property research in the field of textile and clothing. This paper first described the construction methods of fabric finite element models by some scholars at present. The geometric model construction methods are divided into two categories. One is based on the experimental data to generate the model, and the fabric finite element model is constructed by collecting the experimental image information. This method is suitable for fabric local modeling, and can obtain fine and real fabric structure. The other is based on the physical or geometric generation model, that is, using the actual physical weaving process or geometric parameters to construct the three-dimensional structure of the fabric, and this method is easier to construct periodic boundary conditions. The constitutive model of fabric materials is a key step in constructing finite element models. This paper introduces continuous models, discrete models, and semi-discrete models respectively. The continuous models have the fastest calculation speed, but cannot reflect the internal characteristics of the fabric. By contrast, the discrete models can express the state of yarns or fibers, but the computational cost is high. The semi-discrete models combine the advantages and disadvantages of both. At present, most finite element analysis can be done with finite element software. For several commonly used finite element analysis software, this paper introduced their application fields, advantages and disadvantages. In this paper, the current status of finite element research on the mechanical properties of fabrics is roughly divided into four fields: tensility, bullet proofness, tearing and bending. At present, there are more studies in the two fields of tensility and bullet proofness, and the research materials are mainly woven fabrics.
Although finite element technology plays an important role in the simulation of fabric mechanical properties, there are also some shortcomings, such as the lack of model accuracy, the difficulty of determining material parameters, and the difficulty of setting boundary conditions, which affect the accuracy of simulation results. In view of these shortcomings, this paper put forward four suggestions for the follow-up development of finite element in the field of fabric mechanics. First, it is necessary to apply multi-scale analysis methods, and research feature changes at a more microscopic level while ensuring computational efficiency. Second, it is necessary to develop a higher precision textile tester to obtain more accurate material parameters.
Third, it is necessary to fit the actual environment and carry out multi physical field coupling simulation. Fourth, it is necessary to combine other numerical methods to solve complex problems. It is believed that the finite element technology will play a more important role in the simulation of fabric mechanical properties in the future.
Keywords:
finite element; fabric; mechanical property; stretching; bulletproofing; tearing; bending

