黏性颗粒在不同截面形状纤维表面沉积特性的数值模拟
刘倩倩 尤健明 王琰 孙成磊 JIRI Militky DANA Kremenakova 姚菊明 祝国成


DOI: 10.19398j.att.202306015
摘 要:为了探究黏性颗粒在不同截面形状纤维表面的沉积特性,选择截面为圆形、三角形和十字形的纤维作为研究对象,通过Digimat、Solidworks建模软件构建在空间中呈随机分布的刚性三维纤维体模型;利用计算流体力学和离散单元法耦合的方法,基于laminar流场特征,引入JKR(Johnson-kendall-roberts)接触模型,对黏性颗粒在不同纤维表面的沉积特性进行气-固两相耦合数值模拟。模拟结果表明:在黏性颗粒的运动过程中,过滤机理会随时间而变化。初期,捕集主要依赖纤维表面的吸附作用,而后期主要通过纤维本身和颗粒之间的黏附团聚运动共同实现,形成了“尘滤尘”现象。此外,颗粒间滚动摩擦系数对颗粒在纤维上沉积的影响很大。滚动摩擦系数越大,颗粒之间的接触力链结构越稳定,颗粒更难脱落。在3种截面形状的纤维中,十字形截面的捕集效率最高,三角形次之,圆形最低。该研究探究了黏性颗粒与纤维之间的相互作用,优化了纤维结构和布局,为提高空气过滤材料的过滤效率提供了设计思路和理论参考。
关键词:气-固两相流;纤维表面;黏性颗粒;滚动摩擦系数;颗粒捕集
中图分类号:TS151
文献标志码:A
文章编号:1009-265X(2024)06-0041-11
收稿日期:20230615
网络出版日期:20231031
基金项目:浙江省“尖兵”“领雁”研发攻关计划项目(2023C01194);国家自然科学基金项目(51803182);高等学校学科创新引智计划资助项目(D21011);浙江理工大学基本科研业务费专项资金项目(22202304-Y)
作者简介:刘倩倩(1995—),女,河南开封人,硕士研究生,主要从事空气过滤材料数值模拟方面的研究。
通信作者:祝国成,E-mail:gchengzhu@zstu.edu.cn
纤维过滤材料能够有效地捕捉和去除微小颗粒和悬浮物;其具有细小的孔隙结构,可以通过筛选、拦截和吸附等机制,高效地过滤空气中的杂质,已被广泛应用于空气净化领域[1-4]。目前,国内外研究者对材料过滤性能的评价主要依靠实验测试完成,然而此方法不仅所需时间、人力和原料成本较高,而且无法观察微粒在过滤材料内部的运动轨迹与沉积受力情况。随着计算机技术的发展和研究者对颗粒在纤维集合体内部过滤特性研究的深入,计算流体力学(Computational fluid dynamics,CFD)与离散单元法(Discrete element method,DEM)相结合的方法(CFD-DEM方法)开始用于颗粒在过滤材料内部运动情况的研究。早期的研究者大多使用单纤维模型来研究颗粒与纤维在非稳态耦合过程中颗粒在纤维内部的沉积情况[5-7]。Tao等[8]通过CFD-DEM方法研究了圆形截面纤维阵列的排布方式对颗粒过滤特性的影响,并通过测定压降和过滤效率来表征纤维阵列的过滤性能,发现纤维阵列排布方式不同,颗粒堆积分布规律也不同。高紫圣[9]研究了颗粒间静摩擦系数和滚动摩擦系数对单纤维滤尘的影响,发现颗粒间滚动摩擦系数对颗粒堆积形貌影响较大。Yang等[10]采用CFD-DEM方法模拟单纤维颗粒沉积时,将纤维以及沉积颗粒对细颗粒的捕集作用考虑在内,发现模拟所得的颗粒“树枝状”堆积结构,与实验观测到的单纤维上粉尘沉积结构相吻合;同时观测到已沉积颗粒对背风侧的遮挡效应,并探究了雷诺数、表面黏附系数、颗粒直径因素对过滤过程中颗粒链的形成、弯折的影响。诸文旎等[11]通过随机算法建立了微米级圆形三维纤维模型,基于CFD-DEM方法研究了颗粒表面能、颗粒粒径和碰撞恢复系数对黏性颗粒在纤维内部的运动与沉积特性的影响,结果表明当颗粒表面能减小或恢复系数和粒径增大时都能提高过滤效率。然而,随着纤维生产技术的发展,各种截面形状的纤维不断出现。与圆形截面纤维相比,异形截面纤维具有更大的比表面积、更优良的吸附性能,由异形纤维制备的滤料孔隙率高、容尘量大,在过滤领域具有广阔的应用前景[12]。Raynor[13]采用数值计算方法模拟了截面形状为椭圆形的纤维表面的流动特性并与经验公式结果做对比,验证了数值计算的可靠性。赵洪亮等[14]采用CFD方法模拟了截面形状分别为正方形、三角形、三叶形、椭圆形、六边形的纤维在稳态过滤阶段的过滤特性,并与圆形截面纤维的过滤特性进行对比,发现三叶形截面纤维对颗粒的捕集效率最高。朱辉等[15-16]模拟计算了椭圆纤维结构参数对过滤阻力、捕集效率以及质量因子的影响。模拟结果表明:椭圆形纤维在捕集小颗粒方面具有较高的扩散捕集效率和质量因子;然而,对于以惯性或拦截机制为主的大颗粒,椭圆形纤维的综合过滤性能并不一定始终优于圆形纤维。王戈[17]采用CFD-DEM方法研究了三角形截面纤维体的排布方式对过滤效率的影响,得出了纤维阵列交错排布时的过滤效率高于等间距排布阵列。
目前,国内外研究者探究影响颗粒在纤维体内部沉积团聚的因素,多集中于过滤风速、颗粒粒径、恢复系数、表面能等参数,很少有研究者关注颗粒间滚动摩擦系数的变化对颗粒沉积和团聚的影响。此外,为了简化计算过程,所建立的纤维过滤介质模型也局限于单纤维圆形截面、单纤维异形截面、二维异形截面纤维、三维异形截面规则排列纤维模型,而实际工程应用中用于过滤的纤维过滤材料多为随机、杂乱无序地排列,因此将纤维分布方式设置为规则排列或等间距交错排列,得到的模拟结果与实际测试结果会有较大差异。
本文通过分析实际圆形、三角形和十字形涤纶纤维的结构特征和表面形态,采用Digimat、Solidworks建模软件,分别建立截面为圆形、三角形和十字形在空间中随机分布的三维纤维体模型,利用CFD-DEM方法,引入JKR(Johnson-kendall-roberts)接触模型,将黏性颗粒在纤维体上的沉积和团聚情况进行可视化,探讨颗粒在运动过程中纤维对其过滤机理的变化情况;系统考虑三维随机分布纤维的截面形状以及颗粒间滚动摩擦系数的变化对颗粒力链形态结构和颗粒间法向接触力变化的影响,从而探究颗粒在纤维上沉积数量的变化和对过滤效率的影响。通过研究黏性颗粒与纤维材料的相互作用机理,来改进空气过滤设备的设计、优化纤维结构和布局,以此为提高空气过滤材料的过滤效率提供设计思路和理论参考。
1 三维纤维体结构模型的建立
1.1 纤维体结构分析
圆形、三角形和十字形截面涤纶纤维表面形貌扫描电镜图如图1所示。从图1中可以看出:圆形纤维表面光滑,单根纤维形态接近圆柱体;三角形纤维表面平滑,直径较均匀,纵向呈三棱柱结构;十字形纤维表面光洁,纵向呈凸起和凹陷结构。
1.2 纤维模型的建立
针对截面为圆形、三角形和十字形纤维的表面形貌和结构特征,忽略纤维转曲、弯曲、伸长和直径不均匀情况,利用Digimat、Solidworks建模软件建立外接圆直径为20 μm,长度为200 μm,固体体积分数(Solid volume fraction,SVF)为9%,长、宽、高为200 μm×200 μm×200 μm,截面形状分别为圆形、三角形和十字形,在空间中随机分布的三维刚性纤维模型。
纤维异形化后,其表面积及实际占有空间将大大增加,性能也会发生一系列的变化。衡量异形化程度可用异形度表示。异形度是指纤维截面凹凸曲折的程度和偏离圆形而异形化的程度。其值越接近于0,表示纤维截面形状越趋近于圆形;反之,其值越接近于1,表示纤维截面的异形化程度越大。异形度可用式(1)计算:
D=1-rR(1)
式中:D为异形度;R为异形纤维外接圆半径;r为异形纤维内接圆半径。
纤维形状系数可表示为:
S=L2A(2)
式中:S为纤维形状系数;L为纤维截面周长;A为纤维截面的面积。
圆形、三角形和十字形纤维截面参数见表1。
由式(1)―(2)以及表1计算可得三角形截面纤维径向异形度为0.32,形状系数为15.75,十字形截面纤维径向异性度为0.65,形状系数为31.30。图2所示为三角形和十字形纤维截面图。
图3为由建模软件在图1和图2数据的基础上建立的三维随机纤维体模型。
2 CFD-DEM数值计算
2.1 流体相
采用CFD-DEM方法进行模拟计算,CFD部分采用Fluent中的Eulerian-Lagrangian模型,此模型除了考虑液相和固相之间的动量交换外,还考虑了固体颗粒对流体相的影响[18]。其中流体空气为连续相,采用SIMPLE(Semi-implicit method for pressure-link equations)压力耦合方程组的半隐式算法求解。此方法适用于计算流场中含有大量粒子时的运动轨迹,由此可以得到离散相的分布规律。
连续性方程为:
ρt+Δ·(ρv)=0(3)
动量方程为:
ρdvdt=μΔ2-Δp(4)
本构方程为:
σy=-p+2μvy(5)
式中:Δ为梯度运算符号;p为流体压力,Pa;ρ为流体密度,kgm3;v为流体速度,ms;μ为流体动力黏度,Pa·s;σy为y方向应力,Pa;t为时间,ms。
2.2 颗粒相
颗粒在过滤过程中,存在颗粒之间的惯性碰撞机理、颗粒间吸引力或排斥力[19]。经典的Hertz接触模型只考虑了颗粒的弹性变形,没有将颗粒间的黏附力考虑在内,因此该模型不能精确描述颗粒间因接触力的变化对颗粒在纤维体上沉积团聚情况的影响。JKR接触模型将颗粒定义为软球,计算时考虑了颗粒间相互作用力、颗粒间表面能、恢复系数等因素对颗粒运动的影响,适用于描述颗粒在运动过程中的碰撞作用、颗粒间的黏结力和颗粒之间的接触行为。此外,颗粒间的阻尼系数、弹性刚度和摩擦系数等是由材料的属性来决定的,基于离散单元法模拟计算时可将材料的物理属性、颗粒粒径等因素考虑进去。JKR模型中考虑了摩擦力、法向力、切向力等因素,适用于颗粒间发生明显团聚的情况,因此选用JKR接触模型可以较真实地模拟颗粒和纤维材料的性质。颗粒碰撞机理经简化的接触模型如图4所示。
颗粒的法向接触力Fn由材料表面能、接触半径、接触参数得出:
Fn=4E3Rα3-4πγEα32(6)
式中:
Fn为颗粒法向接触力,N;E*为颗粒等效弹性模量,Pa;γ为表面能,Jm2;α为法向重叠量,m;R*为等效接触半径。
颗粒处于静态黏附平衡状态时的黏附力为:
Fc=3πγRp(7)
FnFc=4aa03-4aa032(8)
a0=9πγR2E13(9)
δn0=12 a20613Rp(10)
式中:
Fc为粘性力,N;
E为颗粒弹性模量,Pa;γ为颗粒表面能,Jm2;α0为颗粒静态黏附时接触半径,m;δn0为颗粒静态黏附时法向重叠量,m;Rp为颗粒半径,m。
颗粒间切向接触力Ft为:
Ft=-μsδtFnδt1-min|δt|,δt,maxδt,max32(11)
式中:δt,max为切向位移最大值,m; μs为静摩擦系数。
模拟过程中忽略颗粒间静电力和范德华力,则颗粒受力与运动方程可表示为:
mpdvpdt=FA+FC+Fn+Ft+mpg(12)
Ipdωpdt=∑ki=1Mi(13)
式中:mp为颗粒质量,kg;vp为颗粒运动速度,ms;FA为颗粒所受曳力,N;FC为黏性力,N;Fn为颗粒间法向接触力,N;Ft为颗粒间切向接触力,N;Ip为颗粒转动惯量,kg·m2;ωp为角速度,rs;Mi为颗粒与颗粒或其他固体壁面间的接触力矩,N·m。
CFD-DEM耦合计算过程中,在一个时间步长内,由Fluent对气相流场进行瞬态求解,待气相流场迭代至收敛后,EDEM开始下一个时间步长并给出颗粒的速度、位置等信息,Fluent再根据由EDEM传输的数据求解气相流场,更新流场后产生新的作用在颗粒上的力,从而完成一个耦合循环流程。
2.3 边界条件与计算工况
用于模拟计算的流体类型为空气,雷诺数Re计算公式可表示为:
Re=ρvlμ(14)
式中:ρ为流体密度,其值为1.225 kgm3,v为流体速度0.1 ms,l为流场总长度,计算域前后流场长度分别为50 μm和30 μm,模型厚度为200 μm,即l=280 μm,μ为流体动力黏度,其值为1.7894×10-5 Pa·s。计算可得雷诺数Re≈1.92。
用于模拟计算的过滤器如图5所示,以三角形
截面纤维为例。为保证进出口气流均匀,沿Y轴正方向设置模型前后流场长度分别为50 μm和30 μm,因雷诺数远小于2300则为层流,选用laminar层流模型。在图5的过滤介质模型中,左侧设置为气流入口和颗粒释放面,右侧设置为压力出口和颗粒逃逸面,纤维表面采用无滑移边界条件,模型四周设置为对称边界条件。空气流速设置为0.1 ms,为保证颗粒与气流间没有相对速度滑移,设置颗粒释放速度与气体流速保持一致,颗粒由生成面产生后随气流一起沿Y轴正方向运动至过滤区域。其中颗粒属性参考常见工业粉尘之一的粉煤灰;纤维模型主要考虑空间结构的差异,属性设置与仿真结果无关。接触参数属性的选取,参考前人模拟经验如表2、表3所示[19-20]。
3 结果与分析
3.1 黏性颗粒在纤维模型内沉积情况可视化以及过滤机理
以圆形截面纤维为例,当颗粒粒径为5 μm,颗粒间滚动摩擦系数为0.03时,颗粒随过滤时间变化的运动和在纤维上的沉积情况如图6所示。在T=1 ms的时刻,此时为过滤初期,大多数颗粒由生成面释放后刚刚运动至纤维迎风面,仅有少数颗粒与纤维发生碰撞黏附沉积在纤维表面;在T=3 ms的时刻,一部分颗粒与洁净纤维逐渐发生碰撞黏附,被纤维表面捕集,此时颗粒间也会发生碰撞作用并在纤维迎风一面出现小颗粒团结构,另一部分颗粒进入纤维内部被后方纤维捕捉,还有较少一部分未被纤维捕集的颗粒随气流运动至出口处逃逸;在T=5 ms的时刻,大多数颗粒堆积在纤维的迎风面一侧,以颗粒群的形式堆积在纤维表面形成明显分布不均匀的“树枝状”结构,而另一部分滞留在纤维内部的颗粒由于团聚形成的滤饼会堵塞纤维间隙,与纤维一起参与深层过滤,致使对后续颗粒的过滤机理由两部分组成,一部分是被纤维本身过滤,另一部分被由颗粒团聚形成的“树枝状”结构和滤饼过滤,即“尘滤尘”作用,这些颗粒结构的作用相当于新纤维,可以对颗粒进行二次捕集。
图7所示为颗粒在纤维上沉积形成的“树枝状”结构这与Schilling等[21]观测到的颗粒在纤维表面沉积与团聚的结果相似(见图8),说明本文对颗粒在纤维上沉积情况的模拟是可靠的。
3.2 颗粒间滚动摩擦系数对颗粒接触力链形态变化的影响
黏性颗粒间因滚动摩擦系数变化而引起颗粒之间接触力的变化对颗粒在纤维上的沉积形貌有较大影响。以三角形截面纤维为例,当颗粒间滚动摩擦系数由0.01增加到0.09时,将颗粒隐藏后,颗粒间接触力链形态随颗粒间滚动摩擦系数的形态结构变化情况如图9所示。从图9中可以看出,当颗粒间滚动摩擦系数小于0.05时,大部分颗粒间接触力链的结构呈非伸直状态。这是由于在颗粒随气流前进
运动过程中,滚动摩擦系数小的颗粒间黏结力更小,颗粒间相对滑动增加,使得已沉积在纤维上的颗粒受其他运动颗粒的碰撞更易脱离纤维体,在此过程中接触力链交互穿插形成折叠结构,从而减小了接触力链的长度。当颗粒间滚动摩擦系数大于0.05时,颗粒间滚动阻尼力随颗粒间滚动摩擦系数的增大而增大,滚动摩擦系数大的颗粒间形成的接触力链更加稳定,使得力链的抗弯性能大大增加,颗粒间因接触碰撞而发生掉落的次数减少,颗粒间总体接触次数就会减少,形成的颗粒接触力链整体结构就又长又直,并在迎风面颗粒堆积密集处的纤维表面
形成树枝状的力链结构,因此颗粒间滚动摩擦系数越大,颗粒间滚动阻尼力也越大,颗粒间接触力链结构就越长直,越不易发生颗粒滑移和掉落,颗粒间接触数量就越多。
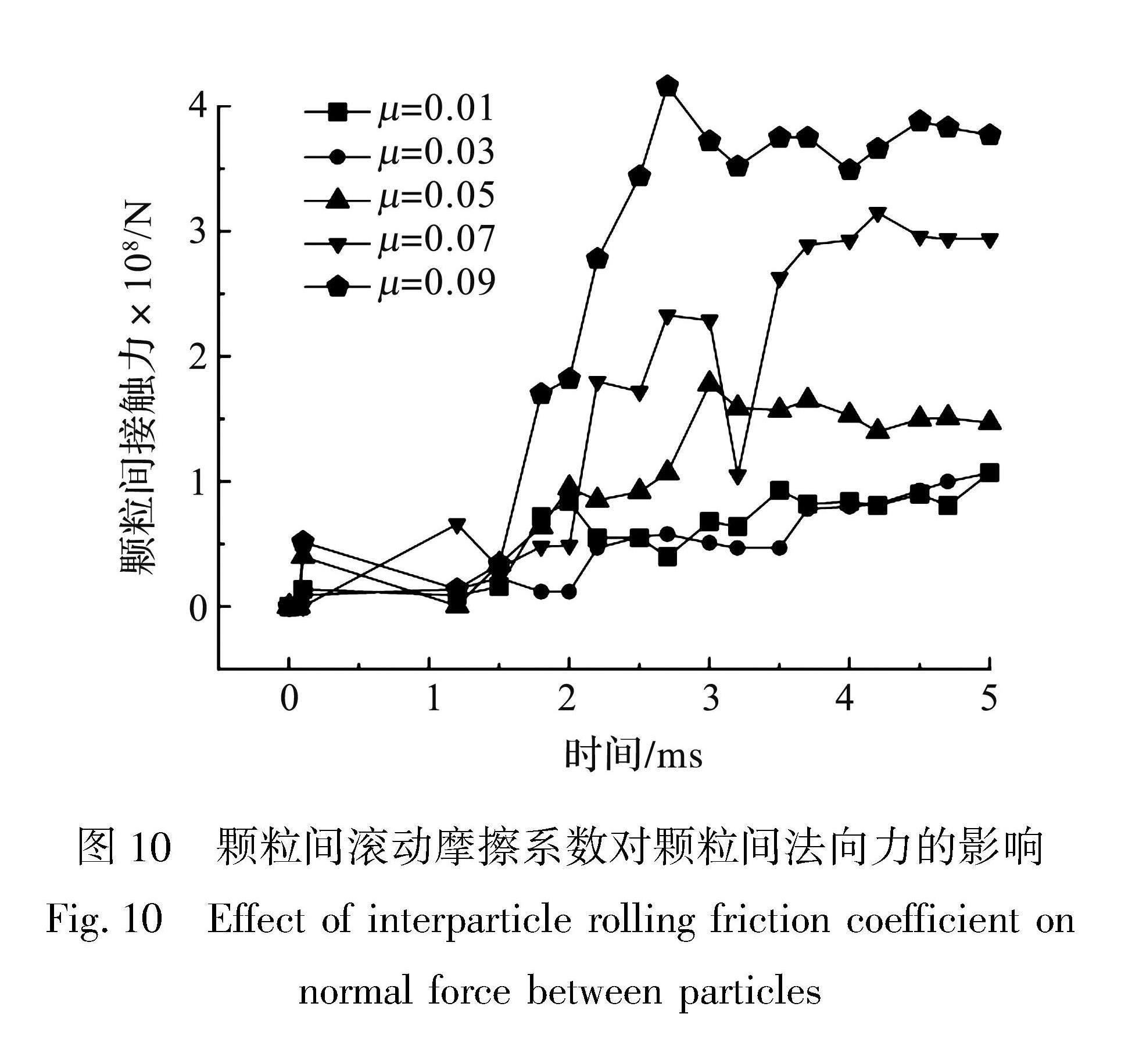
颗粒间法向接触力随颗粒间滚动摩擦系数增大而变化的情况如图10所示。颗粒间的滚动摩擦系数增大,颗粒间法向力随过滤的进行整体呈增大趋势,当颗粒间滚动摩擦系数大于0.05时,此时颗粒间相互接触数量开始增多,与纤维接触数量减少,颗粒间法向力增大趋势更明显。此外,增大颗粒间滚动摩擦系数会使颗粒间的法向弹性力和黏着力增加,而颗粒本身还受到自身重力和曳力的作用,使得颗粒间的相互作用更为紧密,因此颗粒间间隙会减小,相互黏着数量增加。
在三角形截面中,随过滤时间的推进颗粒与颗粒接触数量、颗粒与纤维接触数量的变化情况如表4所示。随滚动摩擦系数增大,颗粒间相互接触的数量有所增多,这会让颗粒在纤维上的沉积形貌产生变化,颗粒堆积形成的“树枝状”结构也会使过滤机理发生改变。
3.3 颗粒间滚动摩擦系数和纤维截面形状对黏性颗粒在纤维上沉积数量的影响
三角形、圆形和十字形截面纤维随颗粒间滚动摩擦系数的增大捕集颗粒数量和过滤效率对比如图11所示。在1.3 ms后,3种截面纤维捕集颗粒数量都随颗粒间滚动摩擦系数的增大有所增加,而在1.3 ms前,颗粒间滚动摩擦系数对捕集颗粒数量的影响并不明显,可能是由于此时产生的颗粒数量较少,颗粒间发生的碰撞几率小;另一方面,此时纤维处于洁净状态,大多数颗粒与纤维接触后直接沉积在纤维上,没有与纤维接触的颗粒从纤维缝隙处随气流继续向前运动至出口逃逸,颗粒间几乎无接触行为,因此此时颗粒间滚动摩擦系数的变化对捕集数量的影响也较小;随着过滤进程的推进,由颗粒生成面释放的颗粒数量越来越多,颗粒间接触和碰撞几率大大增加,而滚动摩擦系数大的颗粒间滚动阻尼力也会增加,颗粒间形成的力链结构更加稳定,使得颗粒在相互接触时更难以移动,法向力的增加也会使颗粒间滑动几率减小,因此颗粒发生碰撞后黏结成团的数量就越多,并在迎风一面形成明显的“树枝状”结构,这种结构会对后续颗粒产生更强的拦截作用。
在T=5 ms的时刻,三种不同截面形状纤维捕集颗粒数量和过滤效率对比图如图12、13所示。当颗粒间滚动摩擦系数为0.09时,十字形截面纤维捕集颗粒数量为721个,捕集效率达到96%,大于三角形和圆形截面纤维,原因是当气流通过十字形纤维时,其表面的凸起和凹槽结构会引起流体的扰动,从而促使漩涡的形成,这种漩涡现象导致颗粒在运动过程中失去了大量的动能,颗粒需要更大的动量才能从凹槽中逃逸,使得颗粒被纤维捕集后更难脱离纤维体。在相同情况下三角形截面纤维捕集颗粒数量大于圆形截面纤维,原因是三角形截面纤维的单根纤维体纵向立体结构呈三棱柱状,与圆形截面纤维相比具有更大的比表面积,可以更好地捕捉到颗粒,因此过滤效率大于圆形截面纤维。因此在实际过滤工程中,应尽可能使用由异形纤维制造而成的滤料。由异形纤维制成的过滤材料相较于圆形纤维拥有更大的比表面积,可供颗粒或污染物黏附和捕获,使容尘量大大增加;另外异形纤维的表面形状可以产生更多的涡流,有助于增加纤维与颗粒之间的碰撞机会,由此来提高过滤效率。
4 结论
本文通过观察和分析实际截面为圆形、三角形和十字形的涤纶纤维表面形貌和结构特征,利用Digimat、Solidworks纤维建模软件建立了纤维直径为20 μm,截面分别为圆形、三角形和十字形在空间中随机分布的三维纤维模型。基于CFD-DEM耦合的方法,在laminar流场下,引入JKR接触模型,分析了在过滤过程中捕集机制的变化机理、颗粒间滚动摩擦系数对黏性颗粒在不同截面形状纤维内沉积特性以及纤维截面形状对过滤效率的影响,主要得出以下结论:
a)颗粒在随时间变化运动过程中的过滤机理会发生改变,在过滤初期,颗粒产生数量较少,主要依靠纤维自身对颗粒的捕集,表面过滤占主导作用。在过滤后期,大多数颗粒堆积在纤维迎风面形成树枝状颗粒群,过滤机理转变为一部分由纤维本身过滤,另一部分被已沉积在纤维上的“树枝状”颗粒群形成的滤饼过滤即“尘滤尘”作用。
b)颗粒间滚动摩擦系数对颗粒在纤维上沉积形态有较大影响。当颗粒间滚动摩擦系数大于0.05时,颗粒间滚动阻尼力和法向接触力也会随滚动摩擦系数的增大而增大,此时颗粒间接触力链更加稳定,减小了颗粒因碰撞而掉落的几率,颗粒间黏着数量增加,在迎风一面形成“树枝状”结构,且滚动摩擦系数越大“树枝状”结构越明显。
c)3种截面形状纤维对黏性颗粒的捕集数量整体上都随着颗粒间滚动摩擦系数的增大而增多,原因是滚动摩擦系数大的颗粒形成的“树枝状”结构越明显,这种结构对后续颗粒有着更强的拦截作用;因十字形纤维表面的凸起和凹槽结构使其捕集颗粒数量大于圆形和三角形截面纤维,因三角形截面纤维的比表面积比圆形截面纤维大,捕集颗粒数量高于圆形截面纤维。
通过探究纤维材料与黏性颗粒之间的相互作用,来优化过滤设备的工作原理和纤维材料本身的结构与布局,最大程度地提高其捕集颗粒的能力,以更高效地去除空气中的颗粒物质,在过滤过程中减少能耗,降低维护成本。
参考文献:
[1]MADDINENI A K, DAS D, DAMODARAN R M. Air-borne particle capture by fibrous filter media under collision effect: A CFD-based approach[J]. Separation and
Purification Technology, 2018, 193: 1-10.
[2]JUNG S, KIM J. Advanced design of fiber-based particulate filters: Materials, morphology, and construction of fibrous assembly[J]. Polymers, 2020,12(8):1714.
[3]MAMUN A, BLACHOWICZ T, SABANTINA L. Electrospun nanofiber mats for filtering applications: Technology, structure and materials[J]. Polymers, 2021,13(9):1368.
[4]刘宇升, 路玉琢, 张田, 等. 芳纶滤料的粉尘过滤性能[J]. 纺织高校基础科学学报, 2023, 36(5):16-22.
LIU Yusheng, LU Yuzhuo, ZHANG Tian, et al. Testing and analysis of aramid fibre needle punced nonwoven fabrics in the application of fitler bags[J]. Basic Sciences Journal of Textile Universities, 2023,36(5):16-22.
[5]BANG J, YOON W. Stochastic analysis of a collection process of submicron particles on a single fiber accounting for the changes in flow field due to particle collection[J]. Journal of Mechanical Science and Technology, 2014, 28(9): 3719-3732.
[6]ABDOLGHADER P, BROCHOT C, HAGHIGHAT F, et al. Airborne nanoparticles filtration performance of fibrous media: A review[J]. Science and Technology for the Built Environment, 2018, 24(6): 648-672.
[7]SALEH A M, VAHEDI TAFRESHI H. On the filtration performance of dust-loaded trilobal fibers[J]. Separation and Purification Technology, 2015, 149: 295-307.
[8]TAO R, YANG M M, LI S Q. Filtration of micro-particles within multi-fiber arrays by adhesive DEM-CFD simulation[J]. Journal of Zhejiang University: Science A, 2018, 19(1): 34-44.
[9]黄紫圣.细颗粒物在纤维上动态沉积过程的理论研究[D].南昌:南昌大学,2020:43-46.
HUANG Zisheng, Theoretical Study on Dynamic Deposition of Fine Particles on Fiber[D]. Nanchang: Nanchang Uni-versity, 2020: 43-46.
[10]YANG M M, LI S Q, YAO Q. Mechanistic studies of initial deposition of fine adhesive particles on a fiber using discrete-element methods[J]. Powder Technology, 2013,248: 44-53.
[11]诸文旎,刘倩倩,JAMSHAID Hafsa,等.黏性颗粒在聚偏氟乙烯纤维膜内部沉积特性数值模拟[J].现代纺织技术,2022,30(5):42-51.
ZHU Wenni, LIU Qianqian, JAMSHAID Hafsa, et al. Numerical simulation of deposition characteristics of viscous particles on the surface of polyvinylidene fluoride membrane[J]. Advanced Textile Technology, 2022, 30(5): 42-51.
[12]郝青青.异形纤维在过滤纸中的应用研究[D].广州:华南理工大学,2018:1-5.
HAO Qingqing. Applied Research of Profiled Fiber In Filter Paper[D]. Guangzhou: South China University of Technology, 2018:1-5.
[13]RAYNOR P C. Flow field and drag for elliptical filter fibers[J]. Aerosol Science and Technology, 2002, 36(12): 1118-1127.
[14]赵洪亮,付海明,雷陈磊,等.纤维截面形状对纤维捕集效率及压力损失的影响[J].东华大学学报(自然科学版),2016,42(1):86-92.
ZHAO Hongliang, FU Haiming, LEI Chenlei, et al. Effect of fibers' cross-sectional shape on fiber capture efficiency and pressure drop[J]. Journal of Donghua University (Natural Science), 2016, 42(1): 86-92.
[15]朱辉,杨会,付海明,等.椭圆纤维过滤压降与惯性捕集效率数值分析[J].中国环境科学,2019,39(2):565-573.
ZHU Hui, YANG Hui, FU Haiming, et al. Numerical analysis of filtration pressure drop and inertial collection efficiency for elliptical fibers[J]. China Environmental Science, 2019, 39(2):565-573.
[16]朱辉,杨会,付海明,等.椭圆纤维对粒子拦截捕集特性的数值计算与分析[J].东华大学学报(自然科学版),2019,45(4):596-604.
ZHU Hui, YANG Hui, FU Haiming, et al.Numerical calculation and analysis of particles interception characteristics by elliptical fibers[J]. Journal of Donghua University (Natural Science), 2019, 45(4):596-604.
[17]王戈,孙志伟,谭蔚,等.异形纤维阵列过滤特性的数值模拟[J].化工进展,2022,41(1):30-39.
WANG Ge,SUN Zhiwei, TAN Wei, et al. Numerical simulation of filtration characteristics on profiled fiber array[J]. Chemical Industry and Engineering Progress, 2022, 41(1): 30-39.
[18]胡国明.颗粒系统的离散元素法分析仿真:离散元素法的工业应用与EDEM软件简介[M].武汉:武汉理工大学出版社,2010:142.
HU Guoming. Analysis and Simulation of Granular System by Discrate Element Method Using EDEM[M]. Wuhan: Wuhan University of Technology Press, 2010: 142.
[19]刘道银,宋诚骁,王铮,等.埋管流化床内湿颗粒流动及混合特性的CFD-DEM数值模拟[J].化工进展,2017,36(6):2070-2077.
LIU Daoyin, SONG Chengxiao, WANG Zheng, et al. CFD-DEM simulation of wet particles flow and mixing behavior in fluidized bed with immersed tubes[J]. Chemical Industry and Engineering Progress, 2017, 36(6):2070-2077.
[20]柳冠青.范德华力和静电力下的细颗粒离散动力学研究[D].北京:清华大学,2011:163.
LIU Guanqing. DiscreteElement Methods of Fine Particle Dynamics in Presence of Vander Waals and Electrostatic Forces[D]. Beijing: Tsinghua University, 2011:163.
[21]SCHILLING M, SCHUTZ S, PIESCHE M. Numerical simulation of the transport and deposition behaviour of particles on filter fibres using Euler-Lagrange Method and coupling of CFD and DEM[C].AIP Conference Proceedings. Xi'an:BioMed Central. 2010:789-795.
Numerical simulation of fiber surface deposition characteristics of viscous particles in different cross-sectional shapes
LIU Qianqian1a, YOU Jianming2, WANG Yan1, SUN Chenglei2, JIRI Militky3, DANA Kremenakova3, YAO Juming1b,4, ZHU Guocheng1,4
(1a.College of Textile Science and Engineering (International Institute of Silk); 1b.Zhejiang-Czech Joint Laboratory of Advanced
Fiber Materials, Zhejiang Sci-Tech University, Hangzhou 310018, China; 2.Zhejiang Zhaohui Filter Technology Co., Ltd., Jiaxing
314511, China; 3.Faculty of Textile Engineering, Technical University of Liberec, Liberec 46117, the Czech Repubilc;
4.Advanced Textile Technology Innovation Center (Jianhu Laboratory), Shaoxing 312000, China)
Abstract:
Numerous researchers focus on the simulation of factors affecting particle deposition and agglomeration within the fiber, while few researchers have paid attention to the changes in the coefficient of rolling friction between the particles on particle deposition and agglomeration. To simplify the process of calculating the fiber filtration media model is also limited to the circular regular arrangement of the fiber model, and if the fiber model and the actual filter media have a lower degree of conformity, the difference between the simulation results and the actual test results will be larger.
In this paper, by observing and analyzing the surface morphology and structural characteristics of polyester fibers with round, triangular and cruciform cross sections,a three-dimensional fiber model with a fiber diameter of 5 μm, an SVF of 9%, and randomly distributed cross sections of round and triangular fibers in space was established by using Digimat fiber modeling software. Based on the CFD-DEM coupling method, the JKR contact model was introduced under the laminar flow field to analyze the changes of the filtration mechanism of the particles during the motion process, the influence of the changes of the rolling friction coefficient between the particles on the deposition characteristics of the viscous particles inside the fibers with different cross-sectional shapes, and the influence of the fiber cross-sectional shapes on the particles trapping efficiency.
The filtration mechanism of particles in the process of time-varying movement changes, and in the early stage of filtration, the number of particles produced is small, mainly relying on the fiber itself to capture particles, while surface filtration plays a dominant role; in the late stage of filtration, most of the particles are accumulated in the windward side of the fiber to form a cluster of dendritic particles, and the filtration mechanism changes to a portion of the capture by the fiber itself, with the other portion of the dendritic particles being deposited in the fiber cluster. The other part is captured by the dendritic particles that have been deposited on the fibers, which is captured by the filter cake formed by the fiber, i.e. "dust filtering dust". When the inter-particle rolling friction coefficient is less than 0.05, the inter-particle adhesion is small, the relative sliding between the particles increases, and the particles adhering to the windward side of the fiber force chain structure are in a non-straightened state; when the inter-particle rolling friction coefficient is greater than 0.05, the inter-particle rolling damping force will increase with the rolling friction coefficient, and then the inter-particle chain of force is more stable, the resistance of the bending performance is greatly increased, and the chain of force structure tends to be longer and straighter, reducing the particles' resistance to bending due to the rolling friction coefficient, reducing the chance of particles falling due to collision, and increasing the number of inter-particle adhesion. The increase of inter-particle rolling friction will increase the inter-particle normal elastic force and adhesion force, the inter-particle interaction is more close, and the number of mutually adhesive particles will also increase; in the three cross-sectional shape fiber model, the number of fibers trapping the viscous particles as a whole increases with the increase of the coefficient of inter-particle rolling friction. At the early stage of filtration, the rolling friction coefficient has less influence on the number of captured particles because the number of released particles is small and the chance of collision between particles is small. With the filtration and the increase of the number of released particles, the collision rate between particles becomes larger, the rolling damping between particles with large rolling friction coefficient increases, the force chain structure formed between particles is more stable, the increase of the normal force makes it more difficult for particles to slip after collision, and the more number of particles adheres to the particles; the number of particles captured is larger than the number of circular and triangular cross-section fibers because of the raised and groove structure of the surface of the cross-shaped fibers, and the specific surface area of triangular cross-section fibers is larger than the number of particles captured by the cross-shaped fibers. The specific surface area of fibers with triangular cross-section is larger than that of fibers with circular cross-section, and the number of particles captured is higher than that of fibers with circular cross-section.
Keywords:
gas-solid two phases flow; fiber surface; viscous particles; coefficient of rolling friction; particle trapping

