纤维性能及细纱捻系数对棉纱断裂强度的影响

吴志刚 张圣男 徐 洁 郁崇文

（东华大学，上海，201620）

单纱断裂强度是衡量成纱质量的重要指标之一，对优化生产工艺、提高成纱质量等都有着重要的指导作用。学者们对于单纱断裂强度预测做了大量研究，如理论模型和智能预测[1]，但多以原棉纤维性能作为主要影响因素预测成纱断裂强度[2-3]，将纺纱工艺参数作为主要影响因素的预测较少。但实践表明，成纱断裂强度不仅与纤维性能有关，还受纺纱工艺参数的影响。

本文考虑的主要因素有纤维性能指标（纤维主体长度/纤维平均长度、纤维短绒率、纤维强度和马克隆值）、纺纱工艺（捻系数），成纱质量指标为棉纱断裂强度。选用回归分析方法，收集不同企业的粗纱，纺成不同规格的细纱，根据棉粗纱中的纤维性能和细纱主要工艺参数（捻系数）来预测细纱断裂强度，并与企业的实际纺纱情况进行对比、验证。

1 试验过程

1.1 粗纱来源

棉粗纱取自南阳海泳纺织制衣企业有限公司、泰兴纺织有限公司、大丰纺织有限公司、郑州一棉有限公司、浙江龙源纺织有限公司、天虹纺织集团和南阳纺织集团，一共12种棉粗纱，编号为1#～12#。

1.2 棉纤维性能

棉纤维细度、平均长度、短绒率的测试仪器为 AFIS 测试仪[4]，马克隆值测试仪器为 HVI测试仪。根据GB/T 14337—2008《化学纤维短纤维拉伸性能试验方法》，测试棉纤维的强伸性能，测试仪器为XQ-1C型高强高模纤维强伸度仪。

1.3 细纱过程

将12种棉粗纱纺成不同捻系数的细纱，设计捻系数分别为 260、300、340、380、420、460和 500，采用X-01型细纱试验机，锭速设置为10 000 r/min～14 000 r/min。

1.4 棉纱性能

根据GB/T 2543.2—2001《纺织品纱线捻度的测定第2部分：退捻加捻法》，对纱线捻度进行测试，仪器为Y331N+纱线捻度仪，预加张力为（0.5±0.1）cN/tex，捻向选择Z捻，加捻方法采用一次加捻退捻法，夹持长度为500 mm。根据GB/T 3916—2013《纺织品卷装纱单根纱线断裂强力和断裂伸长率的测定（CRE法）》进行纱线强伸性能测试，测试仪器为XL-1A型纱线强伸度仪。

1.5 棉纱断裂强度的预测

由于文献[5]单纱断裂强度预测理论模型计算的棉纱断裂强度误差较大，且前人关于棉纱断裂强度预测时考虑纺纱工艺（捻系数）和粗纱中纤维性能的研究较少，而捻系数是很重要的参数，粗纱中纤维性能会直接影响细纱断裂强度，故采用回归方程的方法，构建棉纱断裂强度与粗纱中纤维性能、纺纱工艺（捻系数）的回归方程，实现对棉纱断裂强度的预测。此外，本文收集企业和文献[6]数据，构建棉纱断裂强度与原棉纤维性能、纺纱工艺（捻系数）的回归方程。

2 结果分析及模型建立

2.1 纤维性能测试

采用1.2的测试方法，各粗纱中的棉纤维性能测试结果见表1。

表1 棉纤维性能测试结果

2.2 棉纱断裂强度的预测

2.2.1 捻系数对棉纱断裂强度的影响

棉纱断裂强度随着捻系数的增加先增加后减小。当捻系数增大的时候，棉纤维间的摩擦阻力增加，纤维不易滑脱，但同时由于加捻作用，使得纤维断裂强度的有效分力减小，纤维的断裂不同时性增加；当捻系数较小的时候，滑脱因素起着主导作用，当捻系数较大的时候，纤维断裂强度有效分力减小的负面作用起着主导作用。所以棉纱断裂强度与捻系数的关系为抛物线关系[7]。

本文将取自各企业的12种棉粗纱纺成不同线密度、不同捻系数的细纱。以12#粗纱为例，设计纺纱线密度为29 tex，棉纱断裂强度见表2。

表2 29 tex棉纱断裂强度

根据表2建立棉纱断裂强度与捻系数的回归关系，得到回归方程y=-2.4×10-4x2+0.21x-30.25。其中：x为捻系数；y为棉纱断裂强度。其相关系数为0.941，临界捻系数为438，说明棉纱断裂强度与细纱捻系数有着很强的相关性，随着捻系数的增加先增加后减小，与理论相符。

2.2.2 棉纱断裂强度多元线性回归方程的建立

将取自各企业的12种棉粗纱纺成不同线密度、不同捻系数的细纱，一共122组数据，通过SPSS软件随机挑选约80%数据作为原始数据，建立棉纱断裂强度与粗纱中主要棉纤维性能、细纱捻系数的多元线性回归方程，剩余的20%数据作为验证数据。利用SPSS软件，采用逐步回归的方法进行分析。结果显示：被保留在回归方程中的自变量有捻系数、纤维短绒率、马克隆值和纤维断裂强度，而纤维平均长度被排除。这可能是由于收集的粗纱数目较少，使得纤维平均长度与纤维短绒率呈现较高的线性相关性，导致在逐步回归分析中，纤维平均长度被排除，此时纤维短绒率已经代表了纤维平均长度。在样本中，可以看出纤维平均长度小、短绒率高时，棉纱断裂强度低，与实际情况相符。SPSS软件得出回归方程见式（1）。

式中：x1为捻系数；x2为纤维短绒率；x3为马克隆值；x4为纤维断裂强度。其相关系数为0.859，标准估算的误差为1.297 17，说明建立的棉纱断裂强度回归方程拟合度较好。

回归方程（1）的方差分析见表3。回归方程（1）的回归系数显著性分析见表4。

表3 回归方程（1）的方差分析

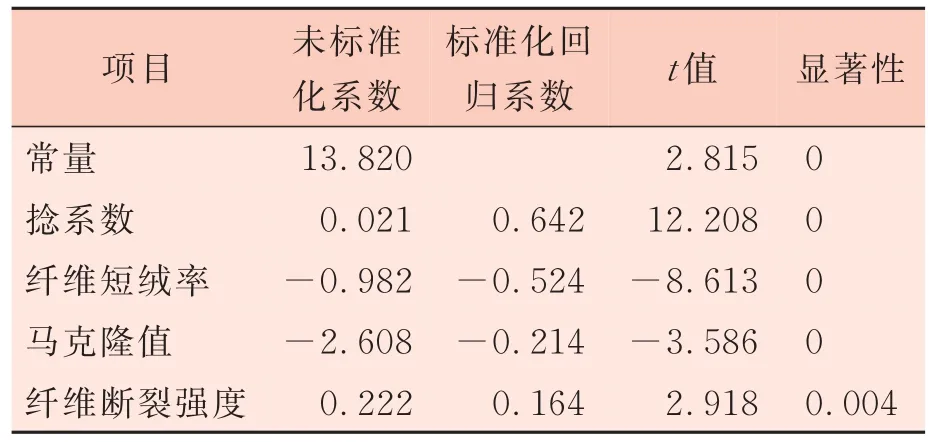
表4 回归方程（1）的回归系数显著性分析

由表3的方差分析可知，方程显著性水平为0，小于0.05，说明建立的棉纱断裂强度回归方程是显著的。由于回归模型中回归系数之间没有直接的可比性，为了得出各自变量对因变量影响的重要程度，一般是将自变量和因变量标准化，将它们变为无量纲的变量，建立标准化回归模型，得到标准化回归系数。根据式（2）、式（3）对变量进行标准化转换。其中：为样本中因变量棉纱断裂强度的均值；k为样本中各自变量的均值；Sy为样本中因变量棉纱断裂强度的标准差；Sk为样本中各自变量的标准差。

转换后，棉纱断裂强度的标准化回归方程为y=0.642x1-0.524x2-0.214x3+0.164x4。根据回归方程中的系数可直接判断，对棉纱断裂强度影响最大的是捻系数，其次为纤维短绒率、马克隆值和纤维断裂强度。

2.2.3 关于捻系数二次项的棉纱断裂强度多项式回归方程的建立

根据理论和文献[8]，棉纱断裂强度与捻系数的关系是抛物线形式。因此在原来的多元线性回归模型中加入捻系数的二次项，由SPSS软件得出回归方程见式（4）。

式（4）的相关系数为0.920，标准估算的误差为1.002 54，说明考虑捻系数二次项的棉纱断裂强度回归方程拟合程度较未考虑捻系数二次项的棉纱断裂强度回归方程好。

2.2.4 考虑交互项的棉纱断裂强度多项式回归方程的建立

在以上的多元线性回归模型和多项式回归模型中，认为只存在主效应，即只考虑每个自变量（捻系数、纤维短绒率、马克隆值、纤维断裂强度）对因变量（棉纱断裂强度）单独的作用，而不受其他自变量取值的影响。但在实际中，会存在条件效应，即某个自变量对因变量的作用可能会依赖其他自变量的取值。例如捻系数对棉纱断裂强度的作用可能会受到纤维短绒率的影响，马克隆值对棉纱断裂强度的作用可能也会受到纤维短绒率的影响。本文利用嵌套模型检验交互项的存在，结果见表5。

表5 受限模型的回归拟合结果

在表5中，模型2～模型7为不受限模型；模型1为受限模型，是将模型2～模型7中交互项（x1x2，x1x3，x1x4，x2x3，x2x4，x3x4）的偏回归系数限制为零。利用模型的嵌套关系，可以对交互项的存在进行统计检验。

以捻系数和纤维短绒率的交互作用是否对棉纱断裂强度有显著性影响为例。模型1不考虑捻系数与纤维短绒率具有交互作用，其回归方程模型为y=a0x12+a1x1+a2x2+a3x3+a4x4+a5；模型2为考虑捻系数与纤维短绒率具有交互作用，其回归方程模型为y=a0x12+a1x1+a2x2+a3x3+a4x4+a5+a6x1x2。其中：a0、a1、a2、a3、a4、a6为回归系数；a5为常数项；x1为捻系数；x2为纤维短绒率；x3为马克隆值；x4为纤维断裂强度。

假设H0：a6=0，H1：a6≠0。根据表 5 的结果，构造检验F统计量，F=3.202，查表可知，F＞F0.（11，93）=2.71，故拒绝原假设H0，认为受限模型1和不受限模型2在数据拟合上有显著性差异，即捻系数与纤维短绒率的交互项x1x2的偏回归系数a6显著区别于零。

同理，在α=0.1显著性水平下，对捻系数马克隆值、捻系数纤维断裂强度、短绒率马克隆值、短绒率纤维断裂强度、马克隆值纤维断裂强度的交互作用是否对棉纱断裂强度有显著性影响进行嵌套模型检验。结果表明，它们的交互作用对棉纱断裂强度均没有显著性的影响，因此只考虑捻系数与纤维短绒率的交互作用。通过SPSS软件得出的棉纱断裂强度回归方程见式（5）。

式（5）的相关系数为0.922，标准估算的误差为0.991 00，说明建立的棉纱断裂强度回归方程拟合程度较好。回归方程（5）的方差分析见表6。

表6 回归方程（5）的方差分析

由表6可知，显著性水平为0，小于0.05，说明建立的棉纱断裂强度回归方程是显著的。

2.2.5 棉纱断裂强度回归方程模型的验证

用样本中剩余的22组数据以及5组取自纺纱企业的数据验证回归方程（1）、回归方程（4）和回归方程（5）的适用性。序号1～22为剩余22组数据，序号23～27为企业数据。回归方程的计算结果和误差见表7。由表7可得，回归方程（1）的误差均值9.58%，回归方程（4）的误差均值7.56%，回归方程（5）的误差均值7.30%，三个回归方程的误差均值接近，回归方程（1）虽然呈线性关系，方程简单但其误差均值相对较大，且无法表示过大捻系数导致棉纱断裂强度降低的现象。回归方程（4）和回归方程（5）的误差均值接近，但是回归方程（4）相对简单。为了简化模型，选择回归方程（4）作为较合适的棉纱断裂强度预测模型。

表7 棉纱断裂强度回归方程的计算结果和误差

3 结论

本文构建了棉纱断裂强度与粗纱中棉纤维的性能、纱线捻系数的回归关系，采用多元线性、多元二次项和多元交互项等3种方法建立了回归方程，并作比较。结果表明：对棉纱断裂强度影响最大的是捻系数，其次为纤维短绒率、马克隆值和纤维断裂强度。三种回归方程的棉纱断裂强度计算值与实测值误差均值接近。为兼顾合理性和简化性，可采用含二次项的多元回归模型。