数形结合法在初中数学解题中的应用技巧
张凤鲜
【摘要】初中数学以研究问题的数量关系与空间形式为主,重视发展学生数学思维.指导学生明确“数”与“形”的内在关联,使学生学会用“以形助数”“以数解形”等技巧解决数学问题,可提高学生的问题分析、求解能力,促进学生思维发展.文章展开论述了数形结合法的内涵及应用意义,探讨了数形结合法在初中数学解题教学中的应用策略,在具体解题过程中的应用技巧,旨在开阔学生学习视野,提高初中数学解题教学质量.
【关键词】数形结合法;初中数学;解题;应用技巧
引 言
数学解题教学是数学教学的重要构成,对于巩固学生基础知识,锻炼学生逻辑推理、数学抽象、建模应用能力有积极意义.《义务教育数学课程标准(2022年版)》提出“避免死记硬背、机械刷题”,倡导教师引导学生结合数学概念、性质、关系、规律探索数学问题的解题技巧,发展学生的数学思维.数形结合法巧妙地将代数、几何解题方法融合在一起,通过“以形助数”“以数解形”等方式将复杂数学问题转化为可直观分析、精准计算的数学问题,从而帮助学生快速解题.新课标背景下,教师有必要探索数形结合法在初中数学解题中的应用技巧,并指导学生学习,在提高学生解题能力的同时发展其数学思维.
一、数形结合法概述
(一)数形结合法的含义
数形结合法以“数”与“形”的对应关系为依据,通过转化问题形式达到解决问题的目的,是一种重要的数学解题方法.数形结合法通过“以形助数”“以数解形”的方式简化问题,使抽象、复杂的难题变得简单、直观,以便于帮助学生把握数学问题本质,体会数学解题的规律性与灵活性.数形结合法一般被用于解决数学问题,通过将抽象的数学语言与直观的几何图形有机结合起来,使学生的抽象思维与形象思维达到和谐统一的状态,从而提高学生对规范图形、代数式的观察分析能力,帮助学生顺利解决问题.实际解题中,数形结合法的应用大致可分为两种情形:第一,借助几何图形的直观特征阐明数之间的关系,达到解题目的.比如,应用函数图像直观说明函数的性质,判断函数的最大值、最小值等.第二,借助数字、公式的精确性与严密性阐述几何图形的某些属性.比如,借助勾股定理公式阐释直角三角形的三边关系等.
(二)数形结合法的应用价值
首先,有利于提高学生理解水平.初中数学理论教学内容具有抽象性.学生只有经历数学理论的形成过程,才能领会其内涵,同时将数学理论合理应用到数学问题解答过程中.应用数形结合法,教师可以指导学生在直观观察图形、推理数学公式的过程中总结数学规律,抽象数学原理,提高学生的理论理解水平.比如,在勾股定理部分的教学中,教师通过出示“毕达哥拉斯家的地砖图形”指导学生用代数公式表示直角三角形三边平方的关系,使学生在“以数解形”的过程中探究数学原理,提高学生对相关知识的理解水平.
其次,有利于提升学生解题能力.数形结合法可实现“数”与“形”的灵活互化,避免学生从单一角度出发解决问题,丰富学生的解决问题途径.比如,解决比较两个一次函数中y值大小的问题时,教师可指导学生将两个一次函数的解析式代入数值,运算后求值、比较大小;教师还可以指导学生应用描点法画出两个一次函数的图像,通过观察图像比较y的大小.
二、数形结合法在初中数学解题教学中的应用策略
数形结合法主张“以形助数”“以数解形”,应用“数形结合”的思想分析问题、解决问题,是一种直观观察与抽象分析并重的解题方法.要在初中数学解题教学中指导学生应用该方法解决复杂问题,就要培养学生良好的解题思维.初中学生思维发展具有递进特征,教师应当按照其思维发展特征组织直观演绎教学、合作讨论教学、练习应用教学等多种教学活动,由此逐步激发其抽象意识,培养其逻辑思维,提升其解题能力.下面,文章将结合人教版初中数学解题教学案例,说明数形结合法在初中数学解题教学中的应用策略.
(一)直观演绎,激发数形结合意识
数形结合法具有应用直观几何图形、位置关系表达抽象数量关系的特点.根据该特点,教师可以在解题教学中组织演绎教学活动,使学生认识到此方法的简便性,激发学生“以数解形”“以形助数”的解题意识.
(二)组织讨论,发散数形结合思维
注入式教学会限制学生的思维,造成其无效学习.要在初中数学解题教学中有效发挥数形结合法的育人作用,需要教师应用生本教学方法代替注入式教学方法,由此发散学生思维,促进其有效学习.为此,教师可以在解题教学中组织讨论活动,通过师生讨论、生生讨论激活学生的具象思维、抽象思维,同时引导学生从不同角度出发分析数学问题,久而久之可提高学生的数形结合思维水平.
以人教版八年级数学下册“勾股定理”一课的解题教学为例,教师可以出示问题,并组织学生讨论:
例2 如图2所示,已知:在△ABC中,∠B=60°,AC=70,AB=30,求BC的长.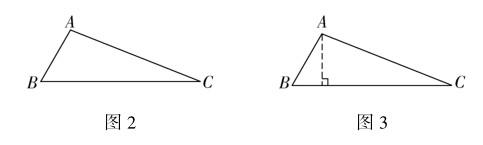
围绕此例题,教师可先提出问题驱动学生思考直角三角形的构造,之后通过组织学生合作讨论发散学生的抽象思维、联想思维,使学生联系勾股定理的代数、几何知识构造直角三角形(见图3),在讨论中求出BC的长.
这样,通过组织讨论发散学生的逻辑、抽象、几何直观思维,使其在讨论中形成绘图构造数学模型、代入数值解决几何问题的数形结合思维.
(三)练习应用,锻炼数形结合能力
“实践出真知.”在初中数学解题教学中组织课内练习、课外练习等多种练习活动,可为学生提供更多实践机会,确保学生在实践中感悟数形结合法的应用优势,同时总结其应用技巧.实际教学中,教师可以先组织学生应用数形结合法解答典型数学问题,再组织其解答变式问题,让其在应用此方法解答多种类型数学题的过程中积累更多解题经验,从而提升数形结合能力.

这样,通过组织学生依次应用数形结合法解答典型例题、拓展例题巩固学生解题学习成果,同时锻炼学生举一反三的迁移思维,确保学生形成应用数形结合法解决初中数学难题的关键能力.
三、数形结合法在初中数学解题中的应用技巧
数形结合法可被用于代数问题、几何问题、统计问题等的解题过程中,通过“以形助数”“以数解形”的方式化简问题,求得答案.下面,文章将结合具体例题,分析数形结合法在数学解题中的应用技巧,以供参考.
(一)解代数问题的应用技巧
解题过程 分别求出两个不等式的解:x-1<0,解得x<1;x+1>0,解得x>-1.使用数轴画出两个解(如图5所示),确定两个不等式解的集合,得到答案:-1
技巧分析 此问题以不等式组的解集为考点,可运用不等式组解集口诀“同大取大,同小取小,大大小小中间找,小小大大找不到”解决.考虑到一些学生记忆力不佳,存在漏记、错记问题,可应用数形结合法,将不等式组内各不等式的解在数轴上表示出来,确定不等式解的交集部分,从而得到问题答案.
(二)解几何问题的应用技巧
例5 如图6所示,在Rt△ABC的直角顶点A在直线a上,斜边BC在直线b上,若a∥b,∠1=55°,则∠2=( ).
A.55° B.45° C.35° D.25°
解题过程 根据已知信息,联想平行线的性质与直角三角形内锐角互余的知识点,观察图形,进行推理:
因为a∥b,
所以∠1=∠ABC=55°;
又因为∠ABC+∠2=90°,
所以∠2=35°.
技巧分析 此题以平行线的性质、直角三角形的性质为考点,数形结合法是解题关键.先对应题目给出的信息找到相应角,再结合观察确定∠1的内错角,结合“两直线平行,内错角相等”这一性质得到∠ABC的角度,再结合“直角三角形的两个锐角互余”这一性质进行数学运算,得到∠2为35°.
(三)解统计问题的应用技巧
例6 某市体育局对某运动队的某体育项目进行测试.测试后队员的成绩分别为7分、8分、9分、10分(满分为10分).依据测试成绩绘制尚不完整的统计图(见图7).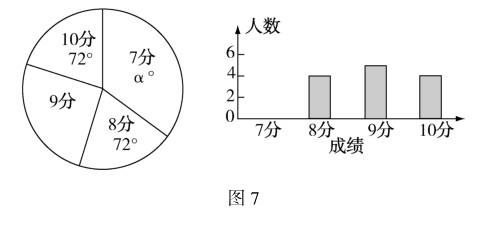

技巧分析 此问题以条形统计图、扇形统计图与中位数、平均数为考点,要求学生综合统计图给出的信息、统计知识解决问题.用数形结合法解决此类问题时,需先识图提炼重点信息,再应用统计模型列式计算,得出问题答案.为保证解题正确率,得到答案后还可将数值代入图形,看是否匹配.
结 语
初中数学解题教学肩负着夯实学生基础知识,锻炼学生解决数学问题能力的重任.初中数学教师应明确数形结合法的含义,在解题教学中指导学生学习数形结合法的一般应用策略,逐渐提高学生的解题能力.
【参考文献】
[1]杨霞,杨其,金晓玲.探究数形结合思想下的初中数学解题策略[J].新课程,2022(41):82-84.
[2]王立仁.借助数形结合思想破解中考题:中考数学压轴题解题技巧分析[J].现代中学生(初中版),2022(22):29-30.
[3]周维.数形结合在初中数学解题中的应用[J].数理天地(初中版),2022(22):33-34.
[4]吴燕琴.数形结合思想下的初中数学解题方法研究[J].数学大世界(上旬),2022(10):59-61.
[5]张嘉铭.数形结合下初中数学典型题解题策略探究[J].数学学习与研究,2022(25):158-160.

