指向逻辑推理素养的初中数学教学策略研究
文/广州市南武中学 李 宁
广州市江南外国学校 吴小敏
逻辑推理素养是数学课程标准提出的六大核心素养之一,是指从一些事实和命题出发,依据规则推出其他命题的素养。 所以,针对初中阶段学生形成逻辑推理素养的关键期,本文立足于课堂实践,研究指向逻辑推理素养的一些初中数学教学策略。
一、“脚手架式的问题链” 设计策略,引导学生层层深入
对于具有一定挑战难度的问题,教师需提供支架,分解难度,助学生寻求知识的突破口。 如在八年级的《最短路径》教学中,两点在某直线的同一侧时, 初学的学生难以想到利用对称的方法, 去确定最短距离时动点在直线上的位置。因此,我们可以先提供两点在直线异侧的简单情境, 学生可以利用 “两点之间,线段最短”轻易求得结论;然后再将其中一点换至另一侧, 就变成了经典的“将军饮马”模型。 有了前面的支架, 学生便自然而然地联想到对称之法,去求最短路径。
二、“变式题组”的设计策略,揭示知识之间的逻辑关联
在数学教学中, 教师通常会在基本概念、 原理、 例题学习的基础上, 再进行一些变式训练。 如能设计变式的题组, 则可以更好地帮助学生体会知识的来龙去脉, 助其融会贯通,发展高阶思维。
案例1.“一线三等角”题组设计与分析
(1)如图1,B、D、E 在一条直线上,ΔABC 为等腰直角三角形,∠ABC=90°, 且AD⊥DE,CE⊥DE.ΔADB 与ΔBEC 全等吗?
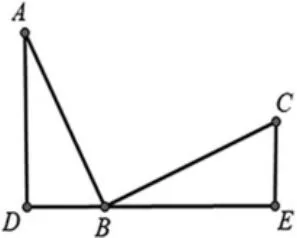
图1
设计理由:“一线三直角” 的图形是一个重要的基本形, 该图形是构成其他各类复杂变式图形的基础。因此,应该紧紧围绕这类基本图形设计水平变式或垂直变式的问题, 帮助学生从不同角度去认识该类图形,由左右两个三角形边、角的关系推出两个三角形之间的关系。
(2)如图2,D、B、E 在一条直线上,∠D=∠ABC=∠E=60°.ΔADB 与ΔBEC 相 似吗?
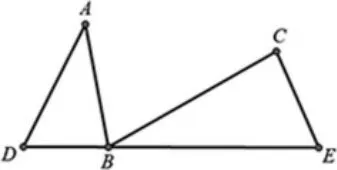
图2
设计理由:此图依然是“一线三等角”图,只是把三个直角换成了三个锐角。 目的是让学生进一步熟悉此基本图。
(3)如图 3,D、B、E 在一条直线上,并且∠ADB=∠ABC=∠BEC.ΔADB 与ΔBEC 相似吗?
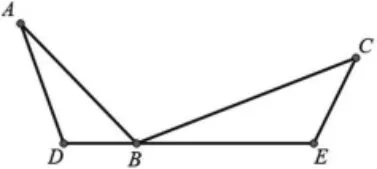
图3
设计理由: 该图是把一线三等角图中相等的三个角都换成钝角,目的是再一次强化学生对基本形在知觉水平上的识别能力。
三、“类比式问题链”设计策略,启发学生进行类比联想
初中阶段, 很多知识点的学习都涉及到类比思想, 用类似的方法去解决类似的问题。 因此可设计类比式的问题链, 启发学生进行联想知识之间的有机联系。 如在笔者执教的《菱形的判定》公开课时,让学生根据矩形的研究路径, 才类比学习菱形的判定方法, 设计如下问题链:矩形是特殊的平行四边形,特殊在何处?菱形是特殊的平行四边形,特殊在何处?除了定义外,矩形的判定方法还有哪些? 这些方法与其性质有何关系?(皆由矩形性质的逆命题得到的)根据菱形的性质,能否猜想其判定方法有哪些?
四、“梳理式问题链” 的设计策略,助力学生建构逻辑网络
例如,在学习《菱形的判定》这一节内容时, 教师可以引导学生在已有知识基础上,将菱形的定义、性质等知识进行整合, 在掌握基本概念和定义后, 学生就可以学习菱形的相关性质和判定。 可采用 “猜想——推理验证——归纳小结——知识运用——总结归纳” 为主线的教学模式,猜想、探索、讨论和推证相结合的方法, 展开教学。 从定义入手,强调要判定一个图形是菱形,首要判断它是平行四边形, 明确在平行四边形的基础上添加相应的条件才是菱形,通过画出菱形,使学生能灵活运用菱形的判定, 由此突破教学难点。 最后以思维导图的形式梳理菱形的所有判定方法, 促其建构几何图形研究的知识网络。

