回归教材基础,彰显创新应用
卢闯


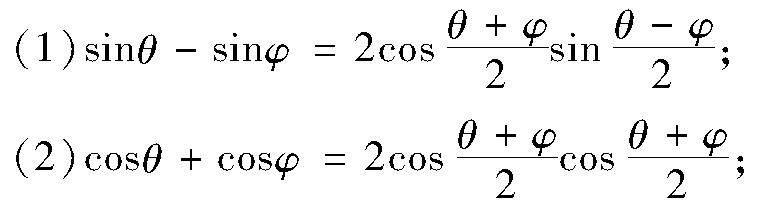
在新教材、新课程、新高考的“三新”背景下,三角函数中的三角恒等变换模块成为高考数学命题的一个基本点,围绕三角函数中的公式以及应用,成为高考命题的一个热点.基于简单的三角恒等变换,特别是和差化积公式与积化和差公式,是三角恒等变换的深度学习与创新应用,对于全面考查学生的“四基”以及数学能力等具有较好的作用,着力数学基础与创新应用,成为高考数学命题中既充分体现知识基础,又体现选拔功能的一类创新考点.
1.回归教材,公式展示
简单的三角恒等变换中的和差化积公式,以例题与练习题的综合形式在现行高中数学教材(2019版人教A版教材必修第一册)中出现.
练习 (人教A版必修第一册P226练习5)求证:
教材中以例题与练习的方式给出和差化积公式,这给深度学习与应用提供更加广阔的空间,也是深度学习与创新应用的一个其他场景.
2.彰显能力,创新应用
在进行三角恒等变换与应用时,特别是利用和差化积公式解决问题时,由于和、积互化时,角度要进行重新组合,因此可能产生一些特殊角或已知角等,对于三角关系式的消项或互约因式等起到很好的变形与转化作用,有利用进行三角关系式的化简求值等,成为三角恒等变形中的一种基本手段,也是深度学习中彰显能力与创新应用的重要场景.
(1)求值问题
分析:根据题设条件,所求的三角关系式中出现了平方关系式,首先三角关系式进行降幂处理,由二次式转化为一次式,之后再利用和差化积公式、积化和差公式等进行三角函数关系式的化简与变形,得以转化与求值.也可以结合填空题中所求结论的确定性,利用特殊值法,选取特殊角来特殊分析与处理.
点评:简单的三角恒等变换中,积化和差公式与和差化积公式是一对“孪生兄弟”,在实际解题过程中,经常离不开两组公式之间的交替使用.要注意的是,在应用和差化积公式时,必须是一次同名三角函数方可以施行;若是异名,必须用诱导公式化为同名;若是高次三角函数,必须用降幂公式降为一次式.
(2)证明问题
点评:根据三角关系式中两角正弦值之和(或差)、两角余弦值之和(或差)的对称或轮换关系时,可以直接借助简单的三角恒等变换中的和差化积公式,通过公式变形与转化来达到化简、变形与求值等方面的应用.注意和差化积公式的熟练掌握,在具体应用中要结合应用场景加以恒等变形与巧妙应用.
(3)判断问题
分析:根据题设条件,抓住题中给出的三角函数关系式的两边比较工整,且均是两角正弦值(或余弦值)的和式,可以直接利用三角函数的和差化积公式加以转化,利用三角函数关系式的恒等变形,并利用角的取值范围来分析与讨论,进而来分析并判断结论的成立.而利用辅助角公式来处理,也是比较常用的一种技巧方法.
点评:该三角函数式问题的判断与应用中,解题方法技巧多樣,通过以上两种方法的分析,相对于解法2来说,解法1直接利用和差化积公式来处理,更加简单粗暴;而解法2通过辅助角公式来处理,作为解决此类问题的一般方法,也不失美感.在实际解题过程中,选择适合自己的技巧方法才是最重要,也是最契合的.
总之,简单的三角恒等变换中的和差化积公式,可以用来处理三角函数中的一些求值、证明或判断等相关问题,可以使得三角函数问题的解决更加简捷有效.而在具体应用和差化积公式时,要注意应用公式之后能否出现特殊角;应用公式之后能否进行提取公因式,能否约分,能否合并或消去同类项等;应用公式之后能否使三角函数关系式的结构更加简单,各种关系更加明显,从而为下一步选用公式进行变换与转化创造条件,是基于深度学习与创新应用的基本要求.

