小学数学“0～9数的认识”单元学习心理过程的建构

徐文彬 陈韵娴 潘禹辰

【摘   要】学生在幼儿园阶段即开始接触“0～9数的认识”单元的相关内容，部分学生在小学入学时对数的认知可能已经达到一年级的部分目标要求。通过编制包含九个操作性任务的一年级新生数感发展水平的测试卷，采用个别面试法，调查并分析了一年级新生的数感发展水平，确定其学习起点。在此基础上，根据APOS理论，建构学生的学习心理过程，预设其在“程序”与“对象”的交替前进中螺旋上升的环形进程，最终整体化为单元概念图式，并迁移应用于解决实际问题的过程中。

【关键词】0～9数的认识；单元整体教学；学习心理过程；概念图式；数感

在幼儿园科学领域课程中，已经涉及了“0～9数的认识”单元的相关内容［1］。在小学入学前，部分学生甚至已经认识了较大数，并能进行简单运算，如20以内数的认识与加减法。为防止教学“简单重复”，笔者基于已经确立的单元知识结构［2-3］，组织一年级新生进行了“数感发展水平”的测试，旨在了解学生的认知起点，预设新知与旧识的联系，建构“0～9数的认识”的学习心理过程。

一、一年级新生数感发展水平的测试

本测试以一年级新生为测试对象，诊断其数感发展水平。

（一）测试卷的编制

笔者借鉴已有实证研究成果，建构了较为全面的一年级新生数感发展水平评价框架（如表1）。然后基于国内外相关研究中已有的测试题［4-7］，结合教材内容，以贴近学生生活经验的情境为依据，按照评价框架编选题目。

本测试采用实物操作与问答相结合的形式。为控制测试时间，笔者通过挖掘各维度之间的关联性（如“计数”和“基数”等），构建了九个主题式情境任务（括号内为主要测试维度）：快速计数小圆点个数（感数）、数数（计数—数词）、统计小熊数量（计数—可数实体、基数）、比较积木数量（比较）、解决围棋子排序问题（数序与序数）、估计围棋子数量（估计）、分一分围棋子（分与合）、解决与铅笔相关的运算问题（加减法、非正式乘除法）、提交答案（比较、估计、分与合、加减法）。各任务下又由易到难设置了1～4题，采取一题多测、多题一测的方式进行设计。一题多测，即一道题可测同一维度的多个连续性水平或不同维度的平行性水平；多题一测，即通过不同任务中的交错题共同验证同一维度同一水平。在此基础上，对各题进行变式，生成多套平行卷。经预测试对试题进行优化，最终形成正式版测试卷。同时制订评价表和记录表，以辨明学生表现所处的水平，尽可能完整记录测试过程。

本测试卷在编制过程中，全程参考相关文件和教材，并采用专家咨询法进行评估和校正，具备较好的内容效度。需要说明的是，本测验卷还需检验复本信度，即通过两个平行测验卷测量同一组被试所得结果的一致性程度。但受工作量和时间限制，暂无法实施检验，留待后续进行。

（二）测试程序的组织

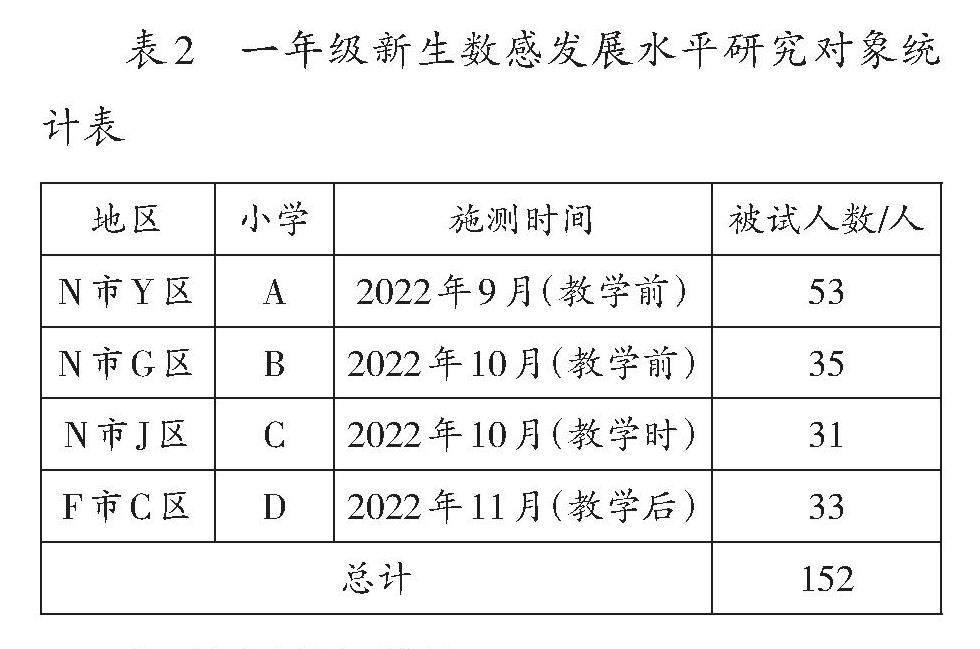
本研究选取N市3所小学及F市1所小学，共计152名一年级小学生作为研究对象（如表2）。其中，D小学为农村小学，整体教育教学水平相对较低，尽管该校学生在测试时已经正式学习过相关内容，但其数感发展的平均水平仍未超过其他3所小学。由此可见，虽然本次测试由于某些客观原因，在施测时间和地点上有一定的局限性，但测试结果并未受到较大的影响。

（三）测试数据的处理

在全面评估同维度各项相关任务的基础上，以主要任务数据为准则、辅助任务数据为参照，根据评价框架，对被试在各维度所能达到的最高水平进行评定。达到水平n的被试，记为n分。将评定的被试各维度的水平情况录入Excel软件，并利用SPSS 26.0软件对信度与效度进行分析。结果显示：Cronbachs a 值为0.747，其信度可以接受；KMO值为0.719，结构效度较好，表明因素分析的适切性较为适中。

二、一年级新生数感发展水平的分析

结合描述统计结果，从质的层面作进一步分析。

（一）一年级新生“数与数量”的发展水平

在“感数”维度，被试的发展水平总体集中于水平3和水平4。其中，0.66%的被试仅达到水平1，无法具体回答看到了“几个”小圆点，只能感知“多”与“少”；6.58%的被试达到水平2，只能识别数量为3个的小圆点集合；39.48%的被试达到水平3，能直观感知并识别数量为5个左右的小圆点集合；33.55%的被试达到水平4，能采用简单的分组策略，识别数量为20个以内的小圆点集合，如将7个小圆点分成“5个”和“2个”或“4个”和“3个”两部分；17.76%的被试达到水平5，能采用跳数策略识别数量超过20个的点集；1.97%的被试达到水平6，能采用分组策略快速识别，知道“5个10是50”。

在“计数—数词”维度，所有被试都能從数词序列中分化出单个数词。其中，13.16%的被试达到水平2，无法从指定起点开始数或只能停于指定终点；44.74%的被试达到水平3，能较好地把握数链的起点与终点；15.79%的被试达到水平4，对自己数了多少个数词有一定的意识；26.31%的被试达到水平5，能自动转变数数方向，有意识地、熟练地正数与倒数。

在“计数—可数实体”维度，被试的发展水平主要集中于水平5，部分被试的最高水平为水平1或水平4，无被试的最高水平为水平2或水平3。其中，6.72%的被试达到水平1，只能数具体（感知）的物体，故无法作答或不能数出被遮挡的小熊；其余被试能摆脱感知单元的依赖，以数词本身为数数实体，但在回答集合总数时存在一定的偏差，故将其判定为水平4，占9.25%。

在“基数”维度，达到水平6的被试最多，占83.55%，说明被试已能从集合元素个数的意义上来理解基数的含义；达到水平5的被试占1.32%，达到水平4的被试占15.13%，这些被试分别使用最大的数词和最后一个数词作为总数。

（二）一年级新生“数量关系”的发展水平

在“比较”维度，1.32%的被试达到水平1，仅能比较同类积木的相等小集合；6.58%的被试达到水平2，能比较数量较少且尺寸相近的两个积木集合，多数能采用计数的方式，但由于他们的数量守恒观念尚未发展，所以无法准确比较尺寸相差较多的两个积木集合，如误认为“大的多”或“颜色占得多的就多”；17.76%的被试达到水平3，具备数量守恒观念，且多数能采用计数方式进行比较。在实物集合比较的基础上，12.50%的被试达到水平4，能比较两个数字的大小，但仅限于一位数；61.84%的被试达到水平5，能准确比较两位数的大小。需要注意的是，水平1至水平3的被试表现出较强的过渡发展趋势，部分被试虽不能比较实物集合的数量，但能准确比较一位数和两位数，这可能与家庭和幼儿园的数学幼小衔接教育有关。

在“数序与序数”维度，5.92%的被试达到水平1，无法对不同大小的围棋子集合进行排序；15.79%的被试达到水平2，能对不同大小的围棋子集合进行排序，但无法区分诸如“3颗棋子”和“第3颗棋子”哪个是基数哪个是序数；20.40%的被试达到水平3，能准确指出某一围棋子是一排围棋子中的第几颗，但无法准确地将一颗围棋子插入其中某一特定位置；5.26%的被试达到水平4，能很好地完成序数放置任务；超过半数的被试达到水平5，能理解数量序列关系中的传递性和可逆性。

在“估計”维度，3.29%的被试达到水平1，能大胆猜测数量，虽出现空间范围估计倾向，但常使用不切实际的大数或小数进行估计，且无法说明理由，如看见一整盘围棋子（60颗）就认为“这么多应该有100颗”，看见比前一盘多时只多估1颗（实际多10颗、15颗、30颗不等）；28.29%的被试达到水平2，能根据围棋子所占空间大小匹配较为合适的数量，但仍超出既定范围；47.37%的被试达到水平3，其估计结果较为合理，且能将估计值与心理数线上的一定范围建立联系；21.05%的被试达到水平4，能运用基准或分组策略进行估计，如“感觉比30多2个10”。

（三）一年级新生“数的运算”的发展水平

在“分与合”维度，约半数的被试达到水平2，能在“分围棋子”的任务中理解围棋子集合之间数量的等量、互补、互换等关系，但无法给出恰当的解释，也无法全面呈现“8颗围棋子”的所有分解形式。22.37%的被试达到水平3，能全面呈现所有分法。25.00%的被试达到水平4，能从抽象层面全面呈现一个数的所有分解形式。在该水平对应任务的测试中，能明显观察到被试“受训练”的痕迹。据不完全了解，部分被试在幼儿园或幼小衔接阶段接触过这类题目。一些学生在填写时会默念如“7可以分成1和6”的口诀；有的学生知道“7的分合有6种（比7少1）”的规律，但解释不清；有的学生能规范有序地依次填入“1、6”“2、5”“3、4”“4、3”“5、2”“6、1”；有的学生虽能准确填写，但不知道为什么这样填。因此，笔者一方面为学生超前的表现感到惊喜，另一方面也反思这样的衔接是否过于重视知识点本身，而忽略了知识背后的道理。

在“加减法”维度，少数被试达到水平1，不理解加减运算的情境而随意作答；25%的被试达到水平2，基本采用数全部的方式得到加减计算的结果；45.39%的被试达到水平3，能通过任意数的方式进行计算；28.29%的被试达到水平4，能较为熟练地运用诸如“凑十法”、根据已知算式推算、交换加数位置等推论性策略展开计算，如由“13+14=27”推算得到“14+13=27”。

在“非正式乘除法”维度，被试的发展水平主要集中在水平2，尚无被试达到水平4。其中，24.34%的被试达到水平1，无法理解乘除运算的情境而随意作答；71.05%的被试达到水平2，能通过在情境图上进行圈画或实物操作得出结果，如“将每3支铅笔分为一组，共4组”；4.61%的被试达到水平3，采用同数加减的策略进行计算，如通过“3+3+3+3=12，加了4个3”，知道“共需4个笔筒”；暂无被试直接依据“4个3是12”得出结果，故无人达到水平4。

根据上述分析，一年级新生具有超出预期的认知起点，因此本单元知识可以也应当作为培养数感的载体，以避免知识的简单重复，使学生在了解、理解、掌握甚至运用部分知识的基础上，根据各自原有的认知水平，实现更大程度的发展。同时，测试中表现出的薄弱点可以确定为本单元学习的难点，如难以区分基数和序数等。

三、“0～9数的认识”单元学习心理过程的建构

在一年级新生数感发展已有水平的基础上，预设其学习心理过程的阶段及具体表现。

（一）“0～9数的认识”单元学习心理过程建构的基础

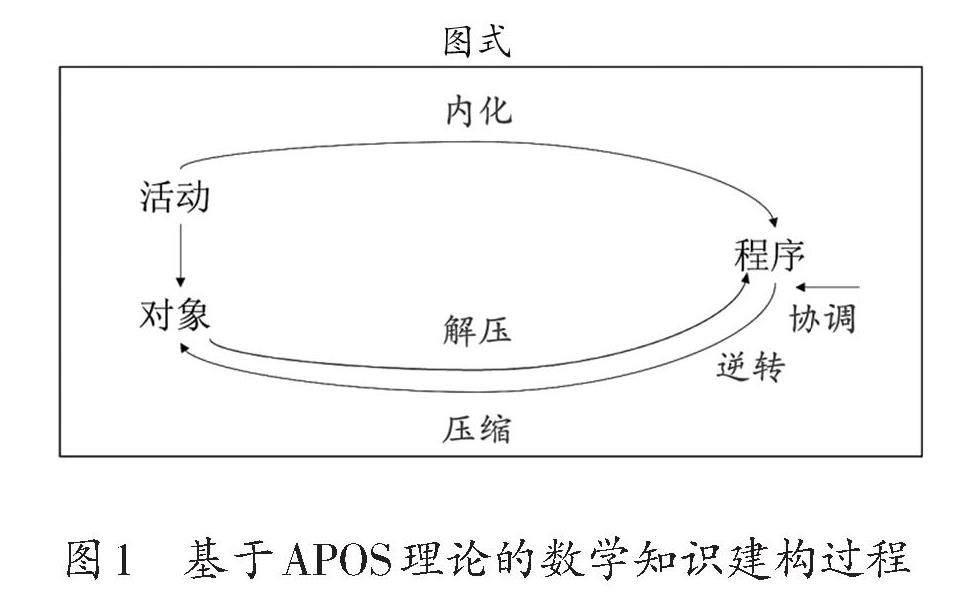
首先，根据皮亚杰儿童认知发展阶段理论，新知的学习应以学生现有认知水平为起点，即以数感发展水平的测试结果为基准。其次，单元知识结构决定了学习内容及其教学方式，为开展学习活动提供了方向。最后，以建构主义为基础的APOS理论适用于数学概念的学习，探讨数学学习的心理结构与心理机制。其中，心理结构由低到高分为活动（Action）、程序（Process）、对象（Object）、图式（Schema）四个层次；心理机制则是促进心理结构形成的方法，包括内化、压缩、解压、协调、逆转等。［8］74

值得注意的是，数学学习心理结构的建立并非简单的线性过程，而是在“程序”与“对象”的交替前进中螺旋上升的环形进程。当“程序”被压缩成“对象”时，存在反向解压的潜在过程，即还原为先前的“程序”，并协调其他“程序”形成新“对象”，或逆转为具有相反意义的新“对象”。综上所述，APOS理论提供了三种学习新知的方式，即“活动—程序—对象”“两对象—两程序—相互协调的程序—新对象”和“对象—程序—逆转后的程序—新对象”（如图1）。［8］76

（二）“0～9数的认识”单元的学习心理过程

APOS理论只是提供了数学知识建构的一般心理过程，下面将结合“0～9数的认识”单元的具体学习内容以及学生实际情况，将知识结构转化为心理结构，并预设相应的学习活动，从而将知识逻辑转化为学习逻辑（如表3）。

上述学习心理过程预设为教学设计提供了参考：阶段1为课前学生的准备状态；阶段2到阶段3的重点是从现实背景中抽象出数，初步理解数0～9的基数、序数的含义；阶段4重点掌握0～9数的顺序；阶段5到阶段6重点掌握0～9数的大小比较；阶段7到阶段8重点掌握0～9数的分解与组成；阶段9到阶段11重点掌握0～9数的加减运算；阶段12回顾并整体建构“0～9数的认识”单元知识结构；阶段13则强调灵活运用所学知识解决实际问题。由于这一学习心理过程预设并未涵盖数的读写、阶段性练习与复习，因此在实际教学中，教师应根据实际情况适当添加相关活动，将其穿插于各阶段之间。

通过对一年级新生的数感发展水平进行诊断，并据此预设“0～9数的认识”单元的学习心理过程，为设计单元整体教学奠定了基础。

参考文献：

［1］中华人民共和国教育部. 3—6岁儿童学习与发展指南［M］.北京：首都师范大学出版社，2012.

［2］徐文彬，陈韵娴，潘禹辰.小学数学“0～9数的认识”单元知识结构的确立（上）［J］.教学月刊·小学版（数学），2023（11）：9-11.

［3］徐文彬，陈韵娴，潘禹辰.小学数学“0～9数的认识”单元知识结构的确立（下）［J］. 教学月刊·小学版（数学），2023（12）：9-14.

［4］克莱门茨，萨拉马. 儿童早期的数学学习与教育：基于学习路径的研究［M］.张俊，陶莹，李正清，等译.北京：教育科学出版社，2020.

［5］周欣.儿童数概念的早期发展［M］.上海：华东师范大学出版社，2004.

［6］赵振国.3—6岁儿童估算和数感的发展研究［D］.上海：华东师范大学，2006.

［7］林嘉绥.儿童对部分与整体关系认识发展的实验研究：Ⅱ.4—7岁儿童数的组成和分解［J］.心理学报，1981（2）：159-167.

［8］马晓丹. APOS理论探索的反思与超越［J］. 教学与管理，2020（33）：74-77.

*本文系全国教育科学“十三五”规划2018年度国家一般项目“中小学STEM教育基本理论与本土实践问题研究”（项目编号：BHA180126）的研究成果。