基于顽固个体的舆论演化动力学研究

许朝瑞 朱月英 江健 刘杰

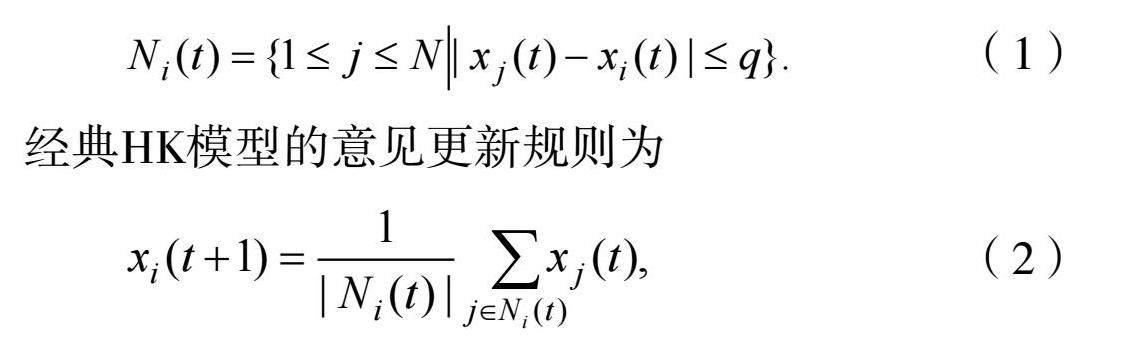
摘 要：由于经典Hegselmann-Krause模型在研究观点演化时没有考虑到个体差异、社会影响力、信息传播的复杂机制等因素，我们在该模型中引入一定比例的顽固个体，并通过网络结构来刻画个体作用之间的差别，进而研究异质群体的舆论演化动力学行为，并分析网络结构和顽固个体比例对舆论演化动力学的影响。结果表明，在没有顽固个体的情况下，高信任阈值会促进共识态的形成，而顽固个体的存在则会导致群体观点的碎片化分布，且高信任阈值并不有利于群体形成局部共识。此外，对比基于度异质性引入顽固个体的不同选择策略下的研究结果发现，选择度较大的个体作为顽固个体时最有利于群体形成局部共识， 网络结构、顽固个体比例和顽固个体的选择策略对系统弛豫时间也有显著影响。这些发现对于揭示真实社会系统中舆论演化的宏观规律和内在机理具有重要意义。

关键词：HK模型；舆论动力学；网络结构；顽固个体

中图分类号：O29 文献标识码：A 文章编号：2095－414X（2024）02－0084－07

0  引言

舆论作为一个独立的综合术语最早出现在18世纪，通常用来描述公众广泛共享的观念、看法、判断或情绪^[1]。舆论是指社会公众在特定事件下表达个体意见，并通过这些意见之间的相互作用形成的观点，是人类特有的社会现象^[2]。舆论动力学是研究舆论形成机制和人类观点演化规律的学科。在重大热点事件中，个体观点通过交互与群体观点互动，促使观点逐步完善。该理论考虑了来自社会文化、民族情感、区域经济、宗教信仰等多方面的影响因素，这些因素源于人类独有的认知、情感和历史等多维因子的综合作用^[3]。舆论的形成是一個动态的、连续的、融合的过程，个体根据群体间意见的相近性不断调整自己的意见，众多意见相互碰撞、影响，使得舆论处于持续演变的状态^[4]。

在前文综述了舆论的历史起源及其动态演变，为了深入地理解和分析这一复杂而动态的社会现象，我们将深入探讨舆论动力学模型，舆论动力学模型主要分为四类：离散舆论动力学模型、连续舆论动力学模型、混合动力学模型和其它动力学模型。常见的离散舆论动力学模型包括：Sznajd模型^[5]、Ising模型^[6]、Voter模型^[7]、Majority rule模型^[8]；连续舆论动力学模型以有界信任阈值模型著称，主要包括Deffuant Weisbuch （DW）模型^[9]和Hegselmann- Krause（HK）模型^[10]，这两种连续舆论动力学模型都将信任阈值作为影响意见演变的主要因素，即个体更偏向于跟与其意见差值在信任阈值范围内的其他个体进行交流^[11]。然而，在DW模型中，每个个体在每一时刻仅与一个满足信任阈值条件的其他个体通信^[12]，但在HK模型中，每个个体^[13]可以同时与多个个体进行通信，这在社交网络中更为现实。根据信任阈值的设置特点可以分别定义同质和异质HK模型。同质HK模型中所有个体的信任阈值都相同，而异质HK模型对不同个体设置不同的信任阈值。

异质HK模型由于考虑了不同个体在信任阈值参数上的差异性，所以能刻画更符合理论实际的舆论演化动力学行为，从而得到了相关领域学者的广泛关注。Lorenz J等^[14]通过研究异质HK模型揭示了具有两种不同信任阈值的社会群体仍然可以在观点上达成共识，且这两种信任阈值都显著低于同质HK模型的临界信任阈值。Kou G等^[15]运用社会分化理论将群体划分为不同信任阈值的意见子群体，进而建立多层次异质群体的舆论动力学模型，分析了异质个体比例、初始意见和群体规模对集体意见演变的影响。Yang Y 等^[16]在经典HK模型的基础上引入权重矩阵刻画不同个体在影响其他个体意见改变能力方面的差异性，并进一步研究了加权HK模型的收敛行为。Fu G等^[17]考虑到真实社会系统中异质个体的存在，将系统中的个体分为三类：思想开放个体、思想温和个体和思想封闭个体，通过考虑信任阈值在不同类别个体之间的差异性分析了不同群体的人口规模对舆论演化行为的影响。Chen S等^[18]使用有界信任阈值模型分析了竞争性意见领袖的声誉、顽固性、吸引力和极端性对社会群体共识形成的影响，相关结果强调了领导者的灵活性和吸引力对成功吸引追随者和在竞争环境中取得影响力的重要性。Cheng C等^[19]通过引入群体压力对个体观点演化的影响研究了更符合理论实际的群体舆论演化动力学行为，发现群体压力的存在更有利于系统共识态的达成。Chen G等^[20]在HK模型中引入环境噪声和通信噪声，发现系统在准同步和观点差异上限方面存在相变，揭示了个体异质性可能导致现实中意见难以同步的原因。Xu H等^[21]通过引入媒体素养对HK模型进行改进，媒体素养可以帮助个体更准确地选择邻居进行通信，研究发现改进的HK模型不受置信限制的影响，可以实现更快的通信和更短的收敛时间，同时对环境噪声表现出强大的鲁棒性。Vasca F等^[22]将一个群体分成若干个小群体，研究了个体在异质置信度情况下的舆论演化动力学行为。Bernardo C等^[23]考虑了具有置信阈值适应策略的异质群体舆论动力学行为，提出了在有限时间内达成实际共识的充分条件，而这一条件的获得取决于置信阈值自适应算法参数的稳态实际簇的最大数量的上限。Xu M等^[24]通过考虑有争议问题的单边和双边呈现方式的影响，对经典HK模型进行了改进，并引入了一种基于信息型教育的新型HK模型。

经典HK模型的舆论演化动力学将系统中的个体看成是同质的，即每个个体具有相同的属性，在观点演化过程中，每个个体会根据与其有连边的所有其他个体观点的平均值更新自己的观点。然而，在真实社会系统中，个体总会有不同于他人的属性，如性格特征，兴趣爱好，心理偏向等^[25-26]。基于这一事实，本文中我们在经典HK舆论动力学模型中引入顽固个体，顽固个体由于其性格原因，在观点演化过程中始终坚持自己最初的观点，即观点保持不变。进而研究顽固个体的比例和网络结构对舆论演化动力学的影响。我们在第二部分详细介绍了经典HK模型和基于顽固个体改进后的舆论动力学模型。在第三部分，我们考虑两种网络结构：规则网络和Barabási—Albert（BA）无标度网络^[27]，通过调整模型和网络参数得到数值仿真結果，并对结果进行分析。第四部分对主要结果进行总结。

1  模型介绍

在经典的HK模型中，假设一个群体中有N个体，每个个体都有一个随时间变化的意见值，且，并且这个个体只会与跟自己意见差值在信任阈值范围内的个体交互意见。这种机制是基于一种现实现象提出的，即如果一个人觉得自己的意见与他人相比存在很大差距，他/她就不愿意接受另一个人的意见。个体i在t时刻的邻居集可以表示为

（1）

经典HK模型的意见更新规则为

（2）

其中，表示中元素的个数。

研究发现，随着信任阈值q的增大，系统会从多种观点共存的状态逐渐演变到只有一种观点存在的状态（共识态），也就是说系统会发生从无序态到有序态的相变。但是经典HK模型是在两个假设的基础上建立的：1）平均场极限：系统中的个体充分混合，每个个体以相同的概率与所有其他个体进行交流；2）个体同质：每个个体拥有同等且不依赖于时间的能力，去说服其他个体接受某一观点。但在真实社会系统中，个体总是偏向于跟自己身边的亲人、朋友或同事等少数个体交流，与其他大部分个体交流的概率几乎为零。此外，总会有一些思想封闭的个体，通常称为顽固个体，在系统演化过程中始终保持自己的观点不变。因此，为了研究更符合理论实际的个体观点的演化动力学行为，我们在经典HK模型的基础上通过引入网络结构刻画个体相互作用之间的差别，同时还考虑了一定比例的顽固个体的存在，进而研究网络结构和顽固个体比例对舆论演化动力学行为的影响。

对于每个特定的时间t：如果节点i是顽固个体，则其观点保持不变，

.                      （3）

如果节点i不是顽固个体，则其观点将按照在考虑网络结构影响的基础上修改过的HK模型的演化规则进行更新，

.              （4）

其中，表示中元素的个数，且

，（5）

其中，N是网络中的节点数，是网络邻接矩阵A的元素，定义为：

（6）

我们引入参数p表示系统中顽固个体的比例，取值范围为（0， 1），q表示信任阈值，取值范围（0，1]。此外，个体的意见融合过程是基于网络传播的，而现实中存在多种类型的网络结构，如随机网络模型、小世界网络模型、无标度网络模型等^[28-29]，在本文的工作中，我们旨在研究顽固个体比例以及网络拓扑结构对个体观点演化行为的影响。

2  数值模拟

根据上面建立的模型，我们对系统进行蒙特卡罗模拟。初始时刻，个体的观点在[0，1]之间均匀分布。为了综合考虑顽固个体和个体相互作用异质性的影响，在给定参数p的情况下，对于在规则网络中，我们在系统中随机选择p*N个体作为顽固个体；对于在BA无标度网络中，我们分别通过三种策略选择系统中的个体作为顽固个体。策略1：在系统中随机选择p*N个体作为顽固个体；策略2：选择前p*N个度最大的个体作为顽固个体；策略3：选择前p*N个度最小的个体作为顽固个体，进而分析不同策略下个体观点演化行为之间的差异。

2.1  个体观点随时间的演化

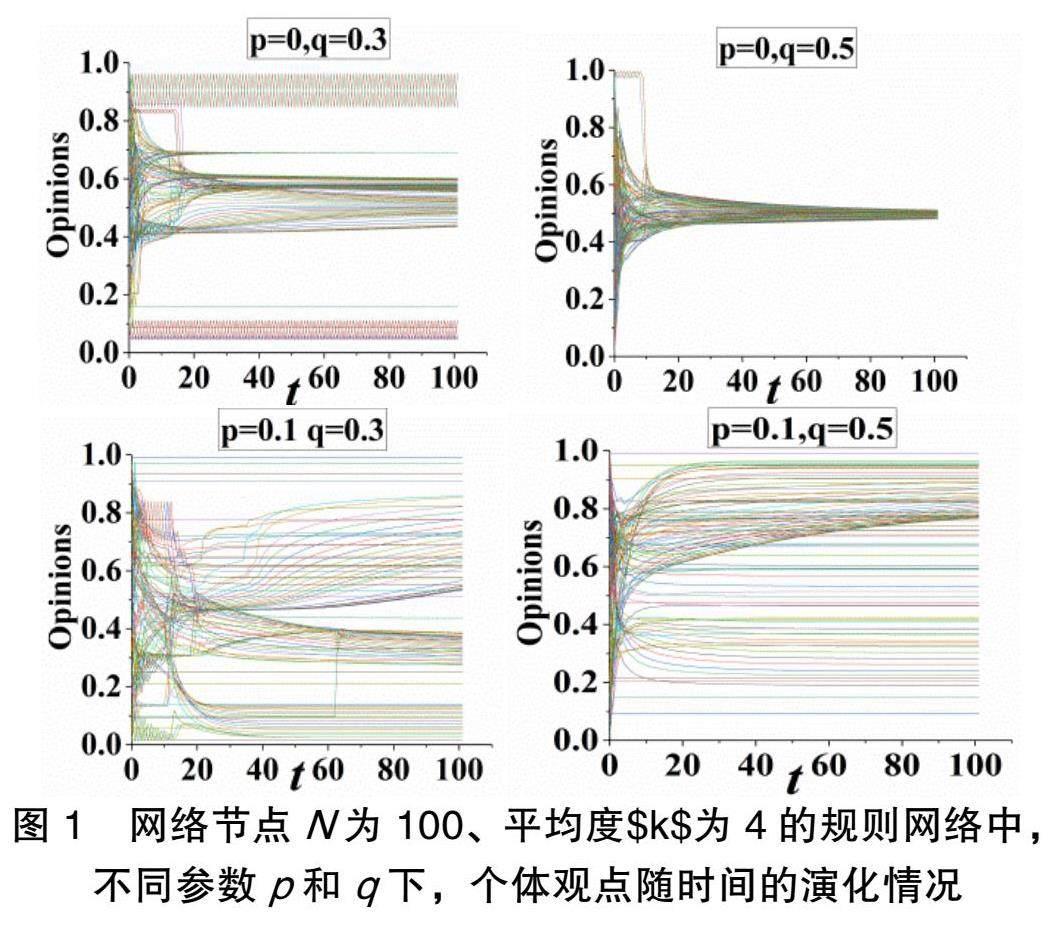
图1描述了网络节点N为100、平均度k为4的规则网络中，不同参数p和q下，个体观点随时间的演化情况。从图中我们可以发现：当系统中没有顽固个体存在，即p=0时，观点演化最终结果会因为q的增大，导致观点由碎片化分布转为共识态。说明当整个系统中没有顽固个体时，信任阈值q的大小将直接影响最终的演化结果。但是当系统中存在顽固个体时，我们发现信任阈值的变化对最终观点演化的影响并不大，都将导致最终观点的碎片化分布。从侧面说明当系统中存在顽固个体时，系统很难达到共识态。

为了考慮网络结构异质性对观点演化行为的影响，接下来我们研究了BA无标度网络上不同参数p和q下个体观点的演化情况，如图2所示。图2（a）- 图2（c）依次对应采取策略1、策略2和策略3设置顽固个体时的观点演化结果。我们发现其最终演化结果和图1中规则网络上的演化结果差别不大，说明当有顽固个体存在时，不同的网络拓扑结构对个体观点的最终演化结果影响不大，但是BA无标度网络上的个体更容易在观点上达成局部共识。此外，对比设置

顽固个体的不同策略下的结果发现，个体观点的演化行为和系统达到稳定态的时间都有所不同。策略1 （随机选择顽固个体）对应的系统达到稳定态的时间最长，但个体观点却最容易形成局部共识，而策略2（选择度大的个体作为顽固个体）对应的系统中的个体最不容易达成局部共识。

2.2  最大社团的分析

从上面研究的个体观点随时间的演化情况可以发现，信任阈值q、顽固个体比例p、顽固个体设置策略以及网络结构对个体观点的聚类行为具有较大影响。因此，下面我们将着重分析个体观点的聚类行为。将观点差值不超过0.01的个体定义为一个社团，我们重点关注系统达到稳定后不同参数对最大社团尺寸的影响。其中为了获得更为稳健和可靠的结果，同时减小由于随机性引起的波动，更好地理解系统的行为，设置系统独立模拟的次数n_s=100，即所有结果都是100次独立模拟下的系综平均值。

我们首先研究了规则网络上不同网络平均度和不同顽固个体比例情况下最大社团归一化尺寸=（，为最大社团中个体的数目）随信任阈值参数q 的分布情况，如图3所示。研究发现：当有顽固个体存在时，最大社团尺寸随参数q的分布会存在一个峰值，且在该峰值附近，网络平均度越大，最大社团尺寸越大。当网络平均度相同时，顽固个体比例越大，最大社团尺寸越小。

接下来我们研究了顽固个体的不同选取策略对最大社团尺寸的影响，相关结果如图4所示。网络节点N为1000，平均度k为10的无标度网络，通过设置不同参数p，得到的最大社团归一化尺寸随参数q的分布情况。从图中可以看出，与规则网络上的结果类似的，当有顽固个体存在时，最大社团尺寸随参数q的分布会出现一个峰值，并且峰值所对应的参数q（约为0.23）的值受顽固个体比例p以及顽固个体选取策略的影响较小。此外，无论采取哪种策略设置顽固个体，顽固个体所占比例p越大，最大社团尺寸越小。我们也发现：当顽固个体所占比例p确定时，相同参数q下，选择度较大的个体作为顽固个体时最大社团尺寸最大，随机选择个体作为顽固个体次之，选择度较小的个体作为顽固个体时最大社团尺寸最小。

图3  在网络节点N为1000的规则网络中，平均度k分别为4（左图）、10（右图），不同参数p下最大社团归一化尺寸随参数q的分布情况

图4  在网络节点N为1000，平均度k为10的无标度网络中，设置不同参数p，得到的最大社团随参数q的分布情况图，从左往右顽固个体的设置依次采取策略 1、策略 2和策略3

为了深入研究网络结构和顽固个体对观点聚类行为的影响，我们进一步分析了最大社团尺寸随参数q分布的峰值大小以及峰值所对应q的值对网络结构和参数p的依赖情况，如图5所示，表示分布的峰值大小，分布的峰值所对应的q的取值用表示。从图5（a）中可以看出最大社团尺寸随参数q分布的峰值会随着参数p的增大而减小，且不同网络结构以及顽固个体选择策略对相关结果的影响变化趋势一致。在图5（b）中，取顽固个体比例p=0.01，研究发现，随网络平均度k的增大而减小，在BA无标度网络中，采取策略2来设置顽固个体，随网络平均度k的变化剧烈，说明对平均度的依赖较强;在规则网络中，的变化较为平缓，不随平均度k的波动而显著变化，对平均度的依赖较弱。

2.3  系統弛豫时间的研究

系统的弛豫时间即系统达到稳定态时所对应的时间步长，在这里我们用表示，从前面个体观点随时间的演化分布图可以发现，网络结构和顽固个体比例对系统弛豫时间都有较明显的影响，因此，我们下面将对此做具体研究。

2.3.1  系统弛豫时间随顽固个体比例的变化情况

我们首先探讨了系统弛豫时间随参数p的分布，研究发现在规则网络下，当p>0时，信任阈值q较小时，随着p增加，系统弛豫时间会先上升然后下降；当信任阈值较大时，系统弛豫时间都会随着参数p单调减小。而在BA无标度网络中，当p>0，无论信任阈值取多大，系统弛豫时间始终随参数p增大而减小。研究还表明，顽固个体的不同设置策略对系统弛豫时间的影响较大，如图6，我们发现随机选择个体作为顽固个体时，系统弛豫时间较长，而当我们选择度值小的个体以及选择度值较大个体的作为顽固个体时，系统弛豫时间相差不大。

图6  不同网络结构和信任阈值参数下系统弛豫时间随参数p的分布图，（a）是在网络节点N为 1000， 平均度k为4的规则网络上的分布图；（b）、（c）、（d）分别对应的是在网络节点N为1000， 平均度k为4的BA无标度网络中，顽固个体的设置依次采取策略1、策略2、策略3得到的分布图

2.3.2  系统弛豫时间随平均度k的变化情况

从图7中我们发现，当网络结构为规则网络时，随着网络的平均度的增加，系统弛豫时间随着k先增加然后保持不变，对于在BA无标度网络中，网络的平均度的变化对系统达到稳定并无太大影响。同时，我们也发现，网络结构的不同对系统达到稳定的时间是有影响的，相同参数情况下，规则网络上系统达到稳定时间大于在BA无标度网络上系统达到稳定的时间。

3  结论

本文中我们主要考察了基于顽固个体的舆论演化动力学行为，通过在规则网络和BA无标度网络上的模拟研究揭示了信任阈值（q）、顽固个体比例（p）、顽固个体设置策略、网络拓扑结构对个体观点演化及聚类行为的显著影响。研究结论如下。第一，顽固个体的存在会导致群体观点的碎片化分布，且高信任阈值并不有利于群体形成局部共识。第二，当系统中存在顽固个体时，最大社团尺寸随信任阈值的分布存在峰值，且峰值对应信任阈值参数的取值对顽固个体比例及顽固个体选取策略的依赖较小；相同参数下，选择度较大的个体作为顽固个体时最大社团尺寸最大，说明其最有利于群体形成局部共识。第三，系统的弛豫时间严格依赖于网络的拓扑结构、顽固个体比例和顽固个体的选择策略，在规则网络中，顽固个体比例的增加初期会导致系统弛豫时间上升，随后下降；而在BA无标度网络中，系统弛豫时间始终随着顽固个体比例的增加而减小，其中顽固个体的随机选择策略导致系统弛豫时间最长。

整體而言，这些实验结果揭示了顽固个体、信任阈值以及网络结构对群体观点演化的复杂影响。顽固个体的存在显著改变了舆论动力学的演化行为，而网络的拓扑结构和平均度也在观点的形成和演化中起到了关键作用。这些发现对于理解社交网络中观点的形成和演化具有重要意义，并为分析社会网络动态、社会动力学模型的建立和实际政策的制定提供了参考依据。

参考文献：

[1]刘怡君， 李倩倩， 牛文元. 舆论动力学模型综述[J]. 管理评论， 2013， 25（1）： 167-176.

[2]王舰， 王志宏， 张乐君. 复杂网络演化的舆论动力学模型及仿真分析[J]. 计算机应用， 2018， 38（4）： 1201-1206.

[3]谭孝勤，陈予恩，李沛. 服饰网络个性化定制体验对购买意愿的影响研究[J]. 武汉纺织大学学报， 2024， 37（1）： 63-70.

[4]向安玲， 沈阳， 何静. 舆论动力学：历史溯源、理论演进与研究前景[J]. 全球传媒学刊， 2020， 7（4）： 99-115.

[5]何晗笑. 社交网络上基于Sznajd型观点模型的动理学建模研究[D]. 华东理工大学， 2023.

[6]徐琳， 陈雨泽， 刘家昊. Monte-Carlo法模拟二维Ising模型：Metropolis、Swendsen-Wang 与Wolff算法的对比[J]. 大学物理， 2022， 41（1）： 79-83.

[7]Yang H， Wang W， Lai Y， Wang B. Convergence to Global Consensus in Opinion Dynamics under a Nonlinear Voter Model[J]. Physics Letters A， 2012， 376（4）： 282-285.

[8]林自展. 在线点评中的舆论动力学研究[D]. 北京邮电大学， 2019.

[9]魏静， 张耀曾， 朱恒民， 等. 基于改进Deffuant模型的舆情观点演化解析[J]. 管理评论， 2022， 34（9）： 147-157.

[10]Wu Z， Zhou Q， Dong Y. Mixed Opinion Dynamics based on DeGroot Model and Hegselmann–Krause Model in Social Networks[J]. IEEE Transactions on Systems， Man， and Cybernetics： Systems， 2022， 53（1）： 296-308.

[11]Blondel V D， Hendrickx J M， and Tsitsiklis. On Krause's Multi-agent Consensus Model with State-dependent Connectivity[J]. IEEE Transactions on Automatic Control， 2009， 54（11）： 2586-2597.

[12]苏炯铭.社会网络上连续观点动力学演化及在线预测应用[D]. 国防科学技术大学， 2014.

[13]Zhao Y， Zhang L， Tang M. Bounded Confidence Opinion Dynamics with Opinion Leaders and Environmental Noises[J]. Computers and Operations Research， 2016， 74： 205-213.

[14]Lorenz J. Heterogeneous Bounds of Confidence： Meet， Discuss and Find Consensus！[J]. Complexity， 2010， 15（4）： 43-52.

[15]Kou G， Zhao Y， Peng Y， Shi Y. Multi-level Opinion Dynamics under Bounded Confidence[J]. Public Library of Science， 2012， 7（9）：e43507.

[16]Yang Y， Dimarogonas D V， Hu X. Opinion Consensus of Modified Hegselmann–Krause Models[J]. Automatica， 2014， 50（2）： 622-627.

[17]Fu G， Zhang W， Li Z. Opinion dynamics of modified Hegselmann-Krause Model in a Group-based Population with Heterogeneous Bounded Confidence[J]. Physica A， 2015， 419： 558-565.

[18]Chen S， Glass D H， McCartney M. Characteristics of Successful Opinion Leaders in a Bounded Confidence Model[J]. Physica A， 2016， 449： 426-436.

[19]Cheng C， Yu C. Opinion Dynamics with Bounded Confidence and Group Pressure[J]. Physica A， 2019， 53（2）： 1-9.

[20]Chen G， Su W， Ding S， Heterogeneous Hegselmann–Krause Dynamics with Environment and Communication Noise[J]. IEEE Transactions on Automatic Control， 2019， 65（8）： 3409-3424.

[21]Xu H， Cai H， Wu S. HKML： A Novel Opinion Dynamics Hegselmann-Krause Model with Media Literacy[C]. In 2020 IEEE International Conference on Systems， Man， and Cybernetics， 2020， 52–57.

[22]Vasca F， Bernardo C， Iervolino R. Practical Consensus in Bounded Confidence Opinion Dynamics[J]. Automatica， 2021， 129： 109683.

[23]Bernardo C， Vasca F， Iervolino R. Heterogeneous Opinion Dynamics with Confidence Thresholds Adaptation[J]. IEEE Transactions on Control of Network Systems， 2021， 9（3）： 1068-1079.

[24]Xu M， Luo Z， Liu R. One-sided Versus Two-sided： A Novel Opinion Dynamics Information-type Education-based Hegselmann-Krause Model[C]. 2021 IEEE International Conference on Systems， Man， and Cybernetics. 2021， 339-334.

[25]陈勇跃， 竺光. 在线教育平台UP主传播影响力评价研究[J]. 武汉纺织大学学报， 2022， 35（5）： 85-91.

[26]刘睿智， 高子欣， 张伟. 战略投资者引入如何促进企业高质量发展[J]. 武汉纺织大学学报， 2023， 36（6）： 87-96.

[27]Barabási A L， Albert R. Emergence of Scaling in Random Networks[J]. Science， 1999， 286（5439）： 509- 512.

[28]Watts D J， Strogatz S H. Collective Dynamics of ‘Small-world Networks[J]. Nature， 1998， 393（6684）： 440-442.

[29]Albert R， Barabási A L. Statistical Mechanics of Complex Networks[J]. Reviews of Modern Physics， 2002， 74（1）： 47-97.

The Study of Opinion Dynamics based on Stubborn Individuals

XU Chaorui，ZHU Yueying，JIANG Jian，LIU Jie

（a. Research Center of Applied Mathematics and Interdisciplinary Sciences; b. School of Mathematical and Physical Sciences，

Wuhan Textile University， Wuhan Hubei 430200， China）

Abstract：Due to the classical Hegselmann-Krause model neglecting factors such as individual differences， social influence， and the complex mechanisms of information propagation in studying opinion evolution， we introduce a certain proportion of stubborn individuals in this model. We characterize the differences in individual interactions through a network structure， thereby investigating the dynamical behavior of opinion evolution in heterogeneous populations. We also analyze the impact of network structure and the proportion of stubborn individuals on the dynamics of opinion evolution. The results indicate that in the absence of stubborn individuals， a high trust threshold promotes the formation of consensus states. However， the presence of stubborn individuals leads to a fragmented distribution of group opinions， and a high trust threshold is not conducive to the formation of local consensus within the group. Furthermore， contrasting research results under different selection strategies for introducing stubborn individuals based on degree heterogeneity reveal that selecting individuals with higher degrees as stubborn individuals is most favorable for the formation of local consensus within the group. The network structure， the proportion of stubborn individuals， and the selection strategy for stubborn individuals also significantly impact the system's relaxation time.These findings are of paramount significance in unraveling the macroscopic patterns and underlying mechanisms of opinion evolution in real-world social systems.

Keywords：HK Model; Opinion Dynamics; Network Structure; Stubborn individual

（責任编辑：田媛苑）