学科核心素养下高中数学教学设计(一)
傅焕铭


一、教材分析
我们收集的原始数据往往多而杂,需要对原始数据进行分析、处理,找到数据背后蕴藏的信息。对总体统计特征的刻画包括两个层面:一是总体统计特征的全面刻画,即刻画出总体中所有个体的取值规律,这个规律可以用总体的频率分布表和频率分布直方图描述或近似描述;二是总体部分统计特征的刻画,如平均数、众数、方差、标准差等数字特征。
二、教学目标
(一)核心素养
学生初步习得科学处理数据的能力。
(二)教学目标
(1)学生用频率分布直方图估计样本的众数、中位数、平均数等数据特征。
(2)学生能自行独立计算样本数据的标准差、方差,并知道分别刻画统计的什么特征。
(3)学生会用样本的频率分布估计总体分布,会用样本特征估计总体特征,理解用样本估计总体的思想,并能利用所学知识解决生活中的一些现实问题。
三、教学重难点
教学重点:学生能从频率分布直方图上估计出样本数据特征。
教學难点:学生理解总体分布的概念,形成统计思维。
四、教学过程
师:同学们,前面我们已经研究过通过抽样调查来研究数据的方法,了解了提高样本代表性的一些具体方法,收集数据后,我们要从中找到数据背后包含的信息,方可达到用样本估计总体的目的。今天我们就一起研究“用样本估计总体”。
(一)课前导学
师:同学们,根据自学任务,思考下列问题并完成检测。
任务1:样本数字特征有哪些?如何求?这些特征在频率分布直方图上如何估计?
任务2:样本数字特征是如何反映样本数据的集中趋势和离散程度的?
(设计意图:通过出示自学任务,引导学生自学,相机进行自学效果检测。学生根据自学情况,检测新知中还有哪些内容没有理解和掌握,从而有针对性地学习本节内容,实现高效学习。同时也旨在培养学生良好的学习习惯,指导学生学会学习数学的方法。)
(二)课堂设计
探究一:样本的数字特征1
1.探究:众数、中位数、平均数的概念。
师:请同学们根据概念解释,完成概念名词的填空,并揣摩这些概念的含义。
(1)______:在一组数据中,出现次数最多的数据。
(2)______:将一组数据按大小依次排列,处在中间位置的一个数据(或中间两个数据的平均数)。
(3)______:指一组数据的算术平均数,即■=■(x1+x2+…+xn)。
师指名学生汇报结果,说出每个概念的关键词,并分别进一步解释各概念。
2.探究:在频率分布直方图中估计众数、中位数、平均数。
师:请同学们结合刚刚对这些概念名词的理解和题后解释,完成下面的填空,并揣摩其含义。
(1)______:通常是指频率分布直方图中最高矩形的中点的横坐标。
(2)______:频率分布直方图中,中位数左边和右边的直方图的面积相等。
(3)______:平均数每个小矩形面积与小矩形底边中点横坐标之积的和。
师指名学生汇报结果,说说你是怎么想的。
3.师:根据刚才我们对数据的众数、中位数和平均数的理解,请尝试解决下面的问题。
例1.根据某城市居民月均用水量样本数据的频率分布直方图(如图1),如何估计数据的众数、中位数和平均数?
学生小组合作完成,指名小组代表汇报,师生共同评析。
(设计意图:本环节主要目的是引导学生探究样本的数字特征1,也就是样本数据的众数、中位数、平均数。首先,引导学生通过字面意思理解这些概念,然后再通过三个概念的解释让学生根据自己对概念的理解去匹配相应的概念,达到加深理解概念的目的。其次,通过第二个探究活动,引导学生学会通过频率分布直方图估计众数、中位数、平均数。最后,通过一个例题,加深巩固所学知识,并应用所学知识解决生活中的实际问题,从而达到学以致用的目的,提升学生的数据分析素养。)
探究二:样本的数字特征2
师:我们刚刚探究了样本数字的众数、中位数和平均数,有时候数据的这些特征不足以表征数据的隐含信息,比如,两组数据的平均数相同,哪一组数据更稳定一些呢?这就需要我们探究样本数字的其他特征——标准差与方差。我们继续探究。
1.探究:标准差与方差。
师:请同学们完成下面的填空,并揣摩其含义。
(1)________:如果有n个数x1,x2,x3,…,xn,则用■表示这组数据的平均数,s表示样本的标准差,则s=■。
(2)________:标准差s的平方s2=■[(x1-■)2+(x2-■)2+…+(xn-■)2]。
师指名学生汇报结果,说说是怎么理解的。
2.师:根据刚刚我们对一组数据的方差和标准差的理解,请尝试解决下面的问题。
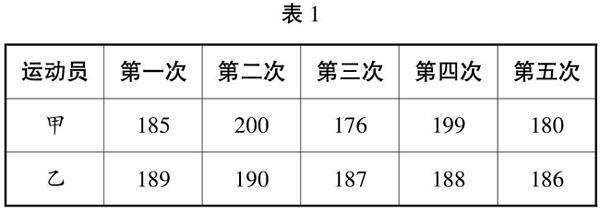
例2.抽样统计甲、乙两位同学的5次跳远测试成绩(单位:厘米),如表1。
(1)甲、乙两位同学成绩的方差是多少?
(2)甲、乙两位同学成绩的标准差是多少?
(3)甲、乙两位同学谁的成绩更稳定?
提示:方差反映样本数据的稳定性,方差越大,数据波动程度越大,方差越小,样本波动程度越小。
学生小组合作探究,然后派小组代表汇报,全班交流,师生共同评析。
(设计意图:引导学生探究样本的数字特征2,即样本数据的标准差和方差,要从字面意思理解这两个概念很难,不像众数、中位数和平均数那样简单,但是,这次给出的概念解释就很简单、明显,学生通过这两个概念的解释很容易匹配相应的概念。但是,学生不太容易理解标准差和方差。接下来,我通过一个例题,让学生以小组合作的形式解决这个问题,使学生在解决实际问题的过程中加深理解标准差和方差,从而降低学生的学习难度,提升学生的数据分析素养。)
师:本节课我们学习样本数据的众数、中位数、平均数、方差和标准差这些特征的目的就是通过样本数字的这些特征去估计总体数字的特征。接下来,我们就一起开启第三个探究活动——用样本的数字特征估计总体数字特征。
探究三:用样本的数字特征估计总体数字特征
师:(多媒体出示例3)请看例3,思考下面的问题。
例3.抽样统计甲、乙两位射击运动员在一次射击测试中各射靶10次的成绩,每次命中的环数如表2:
思考:如果你是教练,如何评价这两位运动员的射击成绩呢?如果选拔一名运动员参赛,你将选谁呢?
学生小组合作探究,然后派小组代表汇报,全班交流,师生共同评析。
師:我们顺利地通过三个探究活动完成了今天这节课的学习任务,了解了样本数据的众数、中位数、平均数、方差和标准差等特征,并能用样本数据特征估计总体数据特征。接下来,我们通过几个题目来检测一下你们究竟学得怎么样。
(三)课堂检测
1.下列说法正确的是( )
A.在一组数据中,平均数的大小决定其方差的大小。
B.平均数反映数据的集中趋势,方差则反映数据离平均值的波动大小。
C.方差是一组数据中每个数据与平均值的差的平方之和。
2.已知一组数据是18,15,10,20,17,这组数据的平均数、中位数、众数、方差和标准差按从小到大的顺序排列为( )。
3.若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为( )
A.8 B.15
C.16 D.32
学生独立完成后,教师指名学生汇报,师生共同评析。
(设计意图:从“双减”的角度,通过3个题目巩固学生所学知识,检测学生数学核心素养的生成情况。)
(四)课堂小结
1.梳理所学知识点,形成知识结构。
2.交流学习方法和学习体验。
(设计意图:通过让学生梳理所学知识点,检测学生学习效果和教师教学效果,旨在促进学生学习和改进教师教学,引导学生把零散的知识点形成系统的知识结构并内化于心。让学生交流学习方法和学习体验,目的是引导学生学会学习,总结有效的数学学习方法,同时让学生分享学习数学的美好体验,使学习数学成为学生的一种享受,不断激发学生学习数学的兴趣。)
五、教学反思
本节内容中对统计的学习,主要是通过一些实际问题案例,让学生经历数据处理的全部过程,在处理过程中理解统计的基本思想方法,逐步形成统计观念,使学生养成尊重事实、用数据说话的生活态度,在解决实际问题中发展学生的数据分析能力。对于学科素养下的高中数学教学,我们应注意以下两点:
(一)设计教学时目标要指向核心素养
在设计教学时,我们不能仅仅围绕教授知识点进行,还要弄清楚核心素养是什么。这节内容的核心素养就是数据分析,在例题教学时,我特别注重让学生经历数据分析处理的全过程,以提高学生的数据分析能力。
(二)教学时活动要指向核心素养
教学活动要为教学目标服务,一切不为教学目标服务的活动都是无效的活动,没有任何意义。在本课教学活动中,每一个探究活动都指向了核心素养。如例1,让学生根据频率分布直方图估计数据的众数、中位数、平均数,是提升学生数据分析能力的一种途径;例2,让学生根据样本数据分析样本的特征,是在锻炼学生的数据分析能力;例3,让学生通过分析样本数据特征,挖掘数据背后的信息,从而科学、合理地对问题做出决策。这样,学生通过参与教学活动,就可以在获得新知的过程中有效提升核心素养。
(作者单位:绍兴市阳明中学)
编辑:温雪莲

