航天器编队飞行相对运动轨迹优化方法综述

陈丹鹤，何敬源，刘幸川，廖文和

（南京理工大学机械工程学院，南京 210094）

0 引言

随着航天领域新型技术不断发展，空间对抗的需求进一步明确，航天器在轨飞行任务变得更加复杂。传统单个航天器集成度高、功能全面，但抗风险能力随着航天器功能的增加而降低；而编队航天器因具备系统成本低和可靠性强的优点，具有较高的抗风险能力。编队是指由两个及以上航天器组成的、具有一定构型的航天器集群，可执行通信、遥感、导航以及侦查等多种任务［1-2］。相比于单个航天器，航天器编队飞行（Spacecraft formation flying，SFF）能够在保证系统功能全面的情况下降低自身风险性，执行更灵活、复杂的空间任务。

按照航天器编队所处的空间环境不同，可以分为近地编队飞行和深空编队飞行。近地编队通常执行遥感观测［3-4］和技术验证等在轨任务，例如美国于2018 年发射的GRACE-FO（Gravity recovery and climate experiment-follow on）是地球重力场观测编队航天器，其通过确定两个航天器的相对位置随时间的变化量，计算出地球引力的影响大小，为构建地球重力场提供数据，如今依旧在轨运行。

SAMSON（Space autonomous mission for swarming and geolocation with nanosatellites）是以色列2021 年验证编队航天器长期自主集群飞行的任务。深空编队一般选择在多体系统的平动点附近［5］、Halo 轨道或悬浮轨道等飞行［6］，其应用覆盖引力波探测、行星探测［7-8］和小天体探测［9］等领域。例如，ESA 的LISA（Laser interferometry satellite antenna）任务是由3 个航天器构成空间等边三角形编队［10］，预计于2037 年发射，主要用来测量引力波引起的空间扭曲变化。按照编队航天器之间是否有物理连接或强制性的约束关系可以将编队分为自由编队和绳系编队［11］，自由编队系统在队形控制过程中需要依靠推进器产生推力，绳系编队航天器系统还可通过调整系绳的张力来保持或改变构型。近10 年来全球已经发射在轨运行的编队飞行任务和未来预计发射的典型任务情况详见表1。

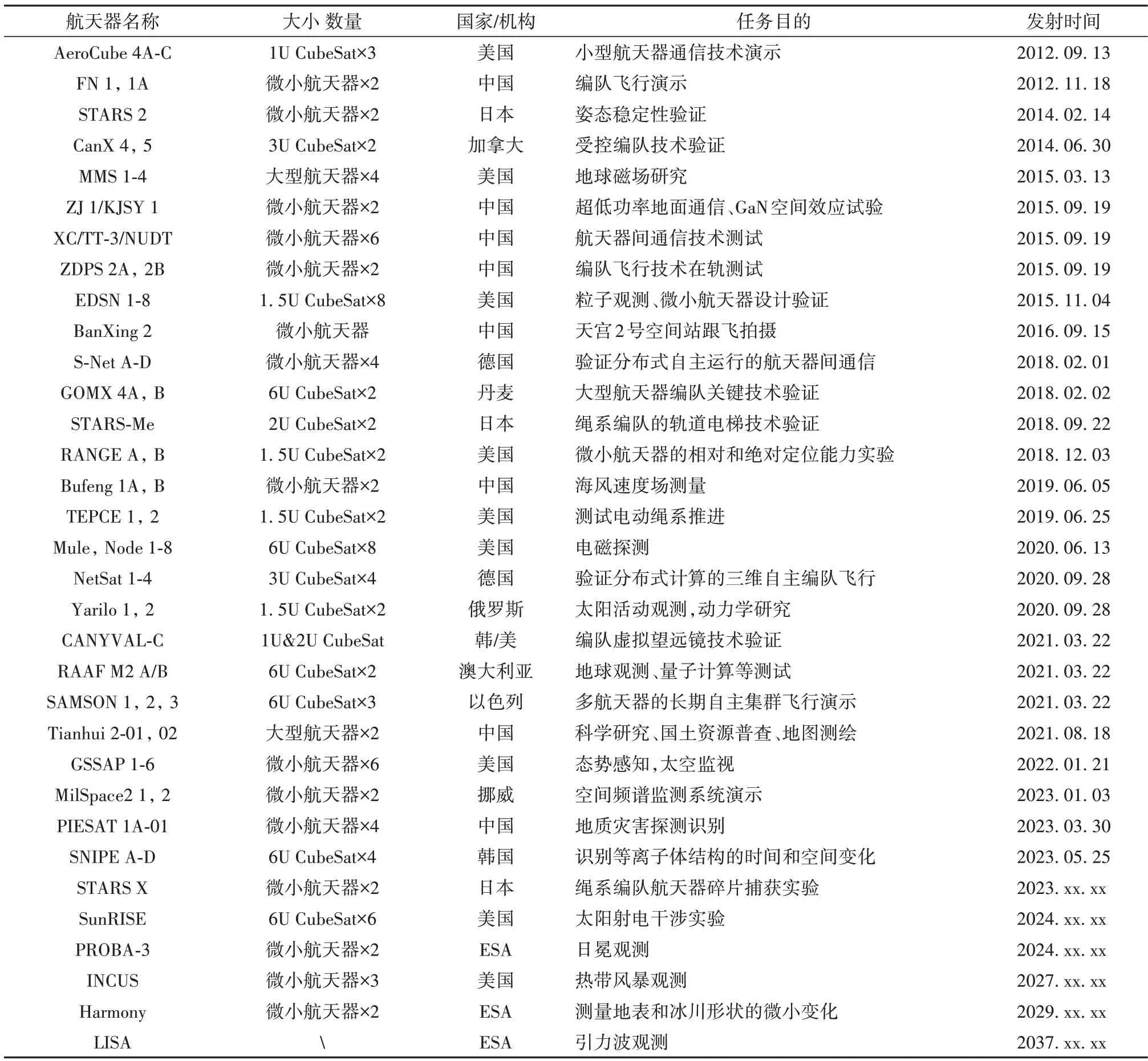
表1 近10年编队飞行任务总结介绍Table 1 Summary formation missions over the past 10 years

面对更加复杂的空间环境和任务要求，航天器编队飞行在队形构建、相对导航和协同制导与控制等方面还有许多问题有待深入研究。从表1可以看出，参与编队飞行任务的主要为微小航天器，然而小型平台携带的燃料以及机动能力有限，在解决编队初始构型设计、构建与重构问题的过程中，如何节省燃料，实现航天器最优飞行转移是重要的环节。

航天器编队飞行构建和重构技术可以分为轨迹规划和轨迹优化两个部分。轨迹规划主要为了确定每个航天器新的空间构型位置，进行构型的分配；轨迹优化则是在满足某个性能指标和多种约束条件下进行轨迹设计。轨迹规划被认为是航天器初始编队稳定部署，以及入轨后编队重构成功的关键问题［12］；另外，选择不同的优化方法是影响星上计算和总体系统性能指标的主要因素。因此，航天器编队飞行构建和重构的轨迹优化问题可以描述为利用集中式或分布式的规划方法，寻找每一个成员航天器的最优轨迹，使每个航天器或者群体能够在规定时间内依据某种性能指标（如燃料、时间等），从当前的编队构型转移到指定构型。然而，通过研究轨迹优化计算得到控制序列（最优轨迹）的过程属于开环控制，无法对系统的实际响应进行实时调整或修正。因此，可以设计控制器跟踪该开环控制轨迹［13］。

研究航天器编队飞行构建和重构的轨迹优化问题，首先需要根据航天器的飞行环境，确定相对运动动力学模型。根据空间范围不同，一般可以分为行星轨道环境（Planetary orbital environments，POE）和深空环境（Deep space，DS）［14］。POE 动力学模型主要为二体运动模型，因此大多以HCW（Hillclohessy-wiltshire）方程、T-H（Tschauner-hempel）方程或相对轨道根数（Relative orbit element，ROE）等构建［15］。在近地环境下，一般采用无摄动的简化模型，或者采用仅考虑J2 效应的动力学模型［16］；而DS 动力学模型大多基于圆型限制性三体问题框架（Circular restricted three body problem，CR3BP）建立［17-18］。

航天器的轨迹优化层需要根据编队任务的需求以及平台能力，确定其构建和重构的性能指标和约束。由于微小航天器携带燃料限制，目标函数多选择为燃料最优［19-20］，约束包含端点约束、系统约束和安全约束等，该问题可用最优控制理论或数学规划方法推导求解。通过最优控制理论的变分法（Calculus of variations，COV）和庞特里亚金极小值原理（Pontryagin's minimum principle，PMP）求解轨迹优化问题［21］。推导一阶必要条件，把最优控制变量表示为状态变量和协态变量的函数，然后将轨迹优化问题转换为两点边值问题（Two-point boundary value problem，TPBVP）求解。此类方法的优点是无需对性能指标寻优，只要满足一阶必要条件的收敛解，即被认为是最优轨迹，且只要初值猜测较精准，就能快速得到收敛解。缺点是难以有效集群避障或是约束大型航天器集群之间的相对位置［16，22］。

另外也可以通过离散空间的方法将轨迹优化问题转换为二次规划（Quadratic programming，QP）、混合整数线性规划（Mixed integer linear programming，MILP）或凸优化问题（Convex optimization，CO）来描述，然后迭代求解。其本质是从数学角度求解非线性规划问题（Nonlinear programming，NLP）［23］。此类方法可以将问题简化，不需要推导一阶必要条件，并且具有更广的收敛域。由于未引入一阶必要条件，不提供协态变量信息，不能保证结果是最优解。虽然该方法可以约束大型航天器集群之间的相对位置，但也会带来大量的运算。对于对集群智能控制响应速度要求较高的系统，若运算时间过长，将大幅降低控制系统的稳定性等性能。因此，如何有效解决编队航天器间相对位置约束问题是编队飞行轨迹优化中较关键和复杂的问题之一。

本文将对航天器编队飞行轨迹优化的相关问题进行综述，首先分析不同环境下的动力学模型与轨迹优化的数学模型；对解决编队飞行的轨迹优化问题的方法进行阐述，并介绍常用的优化软件包和求解器，第3、4 节总结航天器编队飞行轨迹优化相关问题的关键技术需求，以及未来的发展趋势。

1 编队飞行轨迹优化问题的一般描述

1.1 相对动力学模型

在近地轨道环境中的编队飞行，可以看作在主航天器中心建立的笛卡尔坐标系（Local vertical local horizontal，LVLH）下副航天器的运动。设δr=[x，y，z]T和δv=是该坐标系中副航天器的位置和速度向量，其相对关系如图1所示。

图1 近地轨道编队飞行Fig.1 Formation flying in low Earth orbit

对于任意偏心率轨道，副航天器的运动轨迹可通过T-H方程描述如下［24］：

式中：C=(1 -e2)3[n2(1+ecθ)4]，n=，其中sθ和cθ分别表示sinθ和cosθ；x轴沿轨道径向方向，y轴沿迹向方向；e、n、θ分别为主航天器的轨道偏心率、平均角速度和真近点角；dx，dy，dz表示副航天器在轨所受到的摄动力和控制力分量和。

式（1）一般只有在忽略dx，dy，dz项时可获得解析解。通常为了简化航天器近地轨道的相对运动模型，忽略dx，dy，dz项，并假设航天器间相对距离远小于地球半径，即δr/R≪1，且考虑为其在近圆轨道上运动，可以得到HCW方程［25］：

以HCW 方程建立的动力学模型不考虑摄动影响，且表现为线性形式，因此常作为相对运动制导与控制的动力学模型。将线性微分式（2）写为状态空间形式［26］。选择相对位置速度状态向量ψ=，式（2）可采用以下形式表示：

初始条件ψ(t0)=A的特征值为{±nj，±nj，0，0}，因此解中会出现一个长期项。将式（3）以离散空间表示，得到HCW 方程的状态转移矩阵（State transition matrix，STM）：

式中：cnt=cos(nt)，snt=sin(nt)。

在近地轨道环境下，参考轨道可以近似考虑为圆轨道，副航天器可以在笛卡尔坐标系中以HCW方程描述编队飞行运动，但在该模型下轨道递推的误差会随时间累积。为了克服该问题，部分学者选择在模型中考虑摄动因素［27-30］。同时，由于相对运动的HCW 方程中忽略了非线性项，该模型存在长时间预测精度较低的缺点。

在参考轨道为椭圆轨道的情况下，副航天器笛卡尔参数的变化与角动量的变化并不对应［31-32］，此时相对运动方程是时变的，HCW 方程误差较大。因此对于这种情况，采用曲线HCW 模型能够更准确地描述航天器轨道平面内的相对运动［31］，曲线HCW模型以极坐标构建。这使得副航天器与主航天器之间即使迹向距离超过5 km，也能保持较高精度。在航天器远距离机动过程中，曲线HCW 模型与笛卡尔HCW 模型相比递推误差小很多。在曲线HCW模型中系统矩阵A与式（4）的相同，但状态量重新定义为：

为了解决长时间的轨道预报不精确问题，也可以通过建立航天器的相对运动长周期近似模型，得到相对运动的近似解和周期解［33］。但这种通过递推平均相对轨道参数来计算的模型无法推导出考虑密切轨道参数时变的制导和控制策略。

D'Amico 在Lovell等［34］和Schaub等［35］的研究基础上提出了相对轨道根数（ROE）模型，与笛卡尔参数不同，ROE 模型重新定义了相对坐标系下的轨道参数，能够以无量纲形式更简洁地表示航天器之间的相对运动［36-37］。通过对主、副星的开普勒轨道根数进行变换，最终定义一组具有几何关联的相对轨道参数，如式（8）所示：

式中：Ωd、Ωc分别为编队中主、副星的升交点赤经。

线性化动力学模型表示为：

式中：状态转移矩阵Φ随时间迭代，而控制输入矩阵Γ表示在时间Δt时3 个方向控制输入δv的影响。矩阵Φ和Γ可查阅文献［38］获取。

区别于二体问题中的相对运动模型，对于多体问题（深空环境）中的编队飞行任务，例如在圆形限制性三体问题（CR3BP）中推导航天器动力学方程：两个质量为Mi的大天体在相互引力作用下围绕质心旋转，编队航天器质量均满足条件mi≪Mi。定义旋转坐标系S原点为质心，xs轴从M1指向M2，zs轴为系统角动量方向，ys轴为法向，惯性坐标系在参考历元t0=0 处时与旋转坐标系S对齐。通过定义无量纲参数μ=M2(M1+M2)描述两个大天体Mi在坐标系中的位置，其相对关系如图2所示。

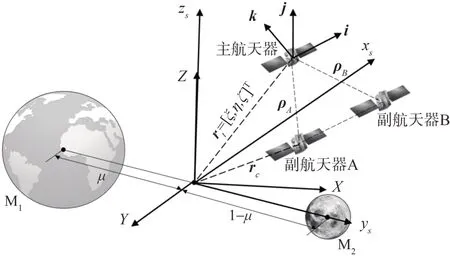
图2 限制性三体问题下编队飞行Fig.2 Formation flight in CR3BP

副航天器在旋转坐标系中的微分运动方程如下［17］：

式中：ux，uy，uz为推力加速度，(i∈1，2，3，j∈1，2)表示为：

矢量rt=[ξ，η，ζ]T和rc分别表示主航天器和副航天器在旋转坐标系S中的位置，副航天器相对于主航天器的位置矢量定义为ρ(x，y，z)=rt-rc。将式（10）进一步线性化，就可以得到线性会合模型（Rendezvous linear model，RLM）为：

x=表示相对位置矢量[ρT,]T。

式中：⊗表示并矢积，ei是从第i个大天体指向主航天器的单位向量，ei、κi定义为：

为了简化计算，部分多体问题下的航天器相对动力学模型可以表示为双重积分形式［14，39］，即忽略式（12）中矩阵内的Hessian 矩阵Σ和科氏加速度项Ω，简化后的模型在一些情况下短时间内能够保持较高的精度［40］，例如在L2点附近。

通过图3对编队飞行的相对运动模型进行归纳分类，根据二体或多体问题选取不同的坐标系统和摄动影响级别，对动力学进行建模。

图3 编队飞行动力学模型划分示意图Fig.3 Classification diagram of formation flying's dynamic model

1.2 编队飞行轨迹优化

航天器编队轨迹优化问题是描述在相对运动动力学模型框架下，确定编队构建或重构的性能指标和约束条件。根据飞行任务的不同，例如编队航天器的数量，编队构型设计等，选取合适的性能指标和约束条件，例如集群作战快速掠飞、绕飞，或者燃料最优下的编队构型调整。编队飞行轨迹优化问题即解决满足最优化求解的形式中，从某个初始状态开始到某个末端状态结束的最优控制序列，如图4所示，箭头表示航天器的推力方向。

图4 编队飞行轨迹规划Fig.4 Formation flight trajectory optimization

1.2.1 性能指标

1）时间最优

若设定轨迹优化的指标是编队飞行构建和重构的时间最短［41］，那么相应的成本函数应表示为：

式中：T表示时间步长。

2）燃料最优

若轨迹优化的指标是所有航天器的总燃料消耗最低，对于共有N个航天器的编队飞行任务，燃料最优成本函数表示为：

式中‖ui‖1表示第i个航天器迹向、径向和法向输入的控制量之和。

3）能量最优

若轨迹优化的指标是所有编队飞行航天器的能量最低，则最优成本函数表示为［14］：

从表1 中可以看出，目前参与编队飞行的航天器多为微小航天器，例如立方星等，由于平台携带燃料有限，目标函数常选择为燃料最优或能量最优。当燃料最优问题的优化求解遇到奇异解时，可以通过引入能量最优的性能指标消除奇异性现象。

另外，约束条件是航天器能够成功完成轨道转移的关键因素，在此过程中主要考虑端点约束中的初末态约束，系统约束中的动力学、推力矢量、推力形式和欠驱动约束等；同时编队飞行轨道转移时，还需要考虑和定义安全距离和避障距离，以及工程限制。约束条件的一般形式概述如下。

1.2.2 初末态约束

编队飞行轨迹优化的目标是为每个成员航天器0，1，2，…，i规划随时间变化的控制序列u，实现位于初始位置xi(t0)的航天器i在控制序列u的输入下，经过飞行时间T运动到目标终点位置。初始状态和终点状态被约束为指定的值，表示为［42］：

式中：x0i是第i个航天器的初始状态向量，xfi是第i个航天器的终点状态向量。

1.2.3 动力学约束

编队飞行轨迹优化过程中的中间时刻状态必须与系统动力学保持一致，即航天器在轨道转移过程需要满足动力学系统约束：

假设推力u在整个时间步长中可以连续施加，那么状态方程同样可以使用离散化方法离散到有限的点上，视为在每个时间步长开始时输入控制量。

1.2.4 推力约束

航天器轨道机动的推力方式主要可分为脉冲和连续推力，连续推力发动机以比冲大，效率高等特点在越来越多的空间任务中得到应用。然而连续推力轨迹优化问题较难求解［43］，如果采用6 自由度的推力形式，其推力幅值大小约束可表示为：

对于采用单自由度推力形式的幅值大小限制为：

式中：ui(t)表示任意时刻t下第i个航天器的推力矢量径向、迹向和法向分量。推力极值umax表示每个推进器可用的有限推力。

对于6 自由度推力形式，如果存在±x方向的推进器配置缺省，即在欠驱动情况下，则上式可写为：

其他方向若出现推力缺省，同样可以定义如式（16）的约束条件。

1.2.5 安全约束

1）航天器间距约束

为了避免不同编队成员航天器在构建或重构过程中发生碰撞，需要限制相对距离阈值。考虑在编队构型完成之后的长期在轨飞行任务执行中，需要保证每两个航天器在每个时间步长、运动方向上至少相距指定的最小安全距离阈值，这也可以看作在航天器周围设定一个圆形禁区。

在任意时刻t，每两个航天器i，j之间的相对距离以‖xi(t) -xj(t)‖2表示，该约束可以表示为：

2）羽流约束

编队航天器在机动时，推进器喷气作用会产生一定的羽流，而羽流效应会对其他成员航天器表面材料或者运动轨迹产生影响［44］。因此，在安全约束中需要考虑羽流约束。这种羽流与推进器轴线对齐，为了避免加入姿态约束导致问题复杂化，可以将该问题简化为避碰约束问题：如果推进器没有点火，则不需要添加约束，如果推进器点火，判断其他航天器是否进入该区域。羽流约束用不等式可以表示如下，其中矩阵M包含了是否点火的判别信息：

S=diag(a2，b2，c2)为羽流在长、宽、高3 方向的安全距离，k=1，2，3 代表航天器的径向、迹向和法向。

3）避撞约束

避撞约束与相对距离限制方法类似，不同的是航天器平台需要通过传感器相对定位或地面基站获取障碍物位置信息，并作为个体纳入相对距离约束当中［45-46］。实际情况中障碍物的出现是随机的，因此轨迹优化也必须滚动更新，才能保证航天器的可靠运行。

动力学模型的建立、优化目标以及约束限制影响着编队航天器变轨的精度。因此根据不同的力学环境和编队任务选取正确的动力学模型，搭建合适的优化指标，建立合理的约束函数形式，是为后续正确快速地求解该问题奠定基础。

2 轨迹优化问题的求解方法

上一节介绍了编队重构轨迹优化问题的一般描述。本节将综述解决该问题的方法，以及在连续域或离散空间中求解此类问题的思路和优缺点，并分析其中存在的一些问题。此外，我们还将介绍智能算法的应用以及脉冲控制的解析优化方法，并探讨深空探测编队飞行的轨迹优化问题。最后，我们将总结和介绍常用的优化软件求解器，以帮助解决这类问题。

2.1 变分原理的连续最优控制问题

变分原理求解轨迹优化问题通常需要推导出一阶必要条件，把最优控制变量表示为状态量和协态变量的函数，将问题转换成两点边值问题求解。极值轨迹的一阶必要条件通常使用扩充哈密顿量H导出，因此，编队重构轨迹优化问题表达为：

式中：σ是约束项的拉格朗日乘子，f(x，u，t)是系统约束，N是航天器个数。

局部极值的一阶必要条件为：

由变分法得到用于定义轨迹的优化函数，再通过打靶法进行轨迹参数的迭代调整，以寻找最优轨迹的近似解。打靶法主要基于牛顿迭代法，一般用来求解微分方程的两点边值问题。Rogers等［28］推导相对运动的非线性方程，将能量最优问题转换为两点边值问题，利用MATLAB 的函数pvb4c 打靶求解，其最小能量转移问题与最大值原理中的非线性边值问题的解几乎相同。

同伦法采用拓扑学原理生成非线性系统的收敛级数解，它能灵活地转换解的表达形式，同时在同伦映射算子上提供极大的自由度。因此引入同伦法可以解决打靶法求两点边值问题中对初始预测过于敏感和控制不连续的问题。Li等［47］验证了该方法的有效性，Thevenet等［16］发现该方法适用于求解包括连续推力和脉冲机动的最优控制问题，但其指出对于间接法来说，航天器间碰撞约束仍然是一个难以解决的问题。

2.2 离散空间最优控制问题

受限于编队飞行个体航天器相互间耦合影响的控制问题，连续时间的最优控制可能会导致难以收敛，因此采用离散空间的求解方法可以更快得到近似解。离散空间的求解方法与连续最优控制求解方法不同，它通过将无限维优化问题参数化，将其转换为有限维优化问题从而找到最优解。该方法首先将最优控制问题转换为非线性规划问题，并用线性规划理论求解最优值［48］。其中参数化的方法分为3类［49］：1）只离散控制变量，包括直接打靶法和多重打靶法；2）离散控制与状态变量，包括配点法和伪谱法；3）只离散状态变量，包括动态逆方法和微分包含法等。本小节重点介绍伪谱法的应用、线性规划中的混合整数线性规划，凸规划以及为求解该类问题提出或改进的智能算法。

2.2.1 伪谱法

伪谱法又称为正交配置法，其原理是将原规划问题离散到指定节点上，利用全局正交多项式逼近状态变量和控制变量［50］。根据所选择的配点位置以及插值基函数的不同，伪谱法又分为Legendre 伪谱法（LPM）、Radau 伪谱法（RPM）、Gauss 伪谱法（GPM）、Chebyshev伪谱法（CPM）等。

基于Legendre 伪谱法，Wu等［12，19］设计了航天器编队机动最优控制的开环解，并在后续研究中继续改进优化，相比于其他数值方法，Legendre伪谱法在求解光滑最优控制问题时具有更高的精度和更快的收敛速度。通过Radau 伪谱法，Li［51］发现对于编队重构问题，一般存在多个燃料最低的脉冲解，而小推力解是唯一的。黄宇嵩等［52］考虑翻滚下的非合作航天器抵近绕飞，采用Gauss 伪谱法规划轨迹，并设计姿轨控制器跟踪控制。尽管使用伪谱法求解该类问题被证明是有效的［51-54］，但保持其收敛性问题仍有待研究。

为进一步优化求解或提高计算效率，部分学者通过结合伪谱法和其他算法来解决该类问题。岳晓奎等［55］以伪谱法优化一条初始轨道，再用同伦法优化获得较为平滑的转移轨道和控制曲线。尽管该方法可以满足平滑需求，但其计算量变大。Zhang等［56］结合Legendre 伪谱法和高斯粒子群算法（Gaussian particle swarm optimization，GPSO）算法，在远距离时以不考虑碰撞约束的Legendre伪谱法优化，近距离用GPSO 算法考虑碰撞约束进行优化。这种方法不需要考虑整个过程的碰撞约束，因此在计算时间上具有一定优势，但同时分段的优化导致结果不是全局最优。由于伪谱法可以以较短时间有效处理大规模优化问题，如今被广泛应用于最优控制领域。

2.2.2 混合整数线性规划

混合整数线性规划（MILP）问题是没有二次特征模型的整数线性规划。与线性规划相比，其决策变量同时包含了连续实数和整数变量，在问题中引入整数变量一般是为了对非线性项进行线性化，提高求解效率。

Mauro等［57-58］在大量的算法验证中发现MILP的求解速度因碰撞约束的加入变得非常慢，并且计算时间随着航天器数量的增加指数上升。为了克服这个问题，许多学者就如何增加计算效率展开研究。Richards等［42］将带有避碰和羽流约束的轨迹优化问题线性化为MILP 问题，并提出了线性化的方法和消除冗余约束的方法，一定程度提高了运算效率。黄海滨等［20］提出了一种直接配置混合整数线性规划（Direct collocation MILP，DCMILP）方法，将直接配置法应用于编队重构的混合整数线性规划，该方法在面对大量航天器或配点较多的情况下，计算时间明显减少，但无法保证收敛到最优解。为了加快计算，Cetin等［59］提出可行性混合整数线性规划（Feasibility MILP，FMILP），其运算速度比一般的MILP快约30倍。

2.2.3 凸优化

在最优化问题中，如果一个问题可以简化为凸函数，那么就可以快速获得其最优解，且凸优化的局部最优解就是全局最优解，Rockafellar［60］指出使优化问题变得复杂的是系统的非凸性，而不是非线性，其中对于编队重构轨迹优化问题的凸化难点在于复杂的约束。

Scala等［61-62］，Zhou等［63］将编队飞行轨迹优化问题转换为凸函数的表达形式，并通过CVX 软件包求解。刘幸川等［64］基于ROE 模型建立了考虑推力缺失和安全距离等工程约束的凸优化模型。Scala 等比较了CVX 软件包中的SDPT3 和SeDuMi 等算法的求解效果和仿真时间，相较于SDPT3，SeDuMi 计算速度较快但是结果不可靠。虽然求解凸化问题具有较好的实时性和精度，但编队航天器轨迹优化问题大多为非凸、非线性的问题，如何将其凸化是问题的难点。

为了使编队航天器完成自主构型分配和轨迹规划，Sarno等［27，65］结合凸优化和遗传算法，设计了一种星载自主规划和控制的方法，其中遗传算法求解构型分配问题（Task assignment，TA），而凸优化用来求解轨迹规划问题。Sarno 等还提出了2 种智能管理的方法，包括集中式和分布式，前者由编队主航天器用来分配构型和计算每个航天器轨迹，后者由每个航天器单独处理各自轨道转移。仿真结果证明集中式方法更节省燃料，而分布式方法计算速度更快。

2.2.4 智能算法和机器学习

随着智能算法和机器学习在解决优化问题中的不断创新和应用，一些学者提出了新的智能算法以快速且稳定地求解编队重构轨迹优化问题。Li等［66］将航天器相对动力学模型嵌入到训练环境中，提出了一种基于深度强化学习的航天器编队重构轨迹规划方法，约束中考虑安全距离，该方法计算速度较快，能满足实时轨迹构建的要求。张润德等［67］用凸优化结果作为训练数据DNN（Deep neural networks）求解转移轨迹的最优燃料消耗，并通过鲁棒自适应拍卖算法解决出现故障卫星失联情况的任务分配。

智能算法相较于牛顿法等可以避免梯度信息计算的复杂性，但对计算机资源的消耗比较大。Zhang等［68］，华冰等［69］均基于鸽群算法进行了改进（GPIO，CGAPIO），其仿真结果与PSO 和PIO 等结果相比更具有鲁棒性和有效性。Spiller等［70］以摄动力为控制变量，并用逆动力学粒子群优化算法求解航天器编队重构时间最优问题。Sun等［71］设计了一种基于闭环脑风暴优化算法（Closed-loop brain storm optimization，CLBSO），用以求解双脉冲控制下的多航天器重构优化问题。D'Ambrosio等［72］开发了一种改进磁荷系统搜索算法（Improved of the magnetic charged system search，IMCSS），其计算结果与解析计算出的理想最优机动结果非常接近，且经过蒙特卡洛模拟证明该算法在求解此类问题时具有可靠性和有效性。黄成等［73］提出一种混合蝙蝠算法结合三次样条插值的方法稳定计算出交会与接近的燃料最小路径。

2.3 其他优化方法

一些学者给出了编队轨迹优化问题的不同求解形式。Cho等［74］引入拉格朗日乘子，将这些约束合并到成本函数中推导其解析解。Wang等［75］提出了一种动力学约束表示形式，并引入一个不等式，推导出了燃料消耗的下界和相应的控制力，但其没有考虑安全距离等复杂约束。Wu等［76］通过将规划分为宏观层和微观层，宏观层采用质心沃洛诺伊图镶嵌法避免碰撞，微观层采用MPC（Model predictive control）求得最优轨迹，以更快地求解。王涛等［77］通过构造平衡态构型公式将轨迹规划转化成行为调节参数的设计问题，该方法在保证相对距离约束的情况下也能较快优化轨道。赵腾等［78］提出了一种基于能量最优的聚类避碰算法，优化了计算碰撞距离约束的时间，与传统遗传算法相比计算速度更快。其他研究［79-82］给出了一些基于脉冲推力的轨迹优化求解方法，并同样限制了相对位置距离。相对于连续推力的解，脉冲解在调整编队轨迹时可以提供较大的自由度，但同时也可能引入较大的推力需求。脉冲解通常适用于对轨道变化需求较大、需要快速调整的情况；连续推力解则多用于平滑的轨道调整，但也需要更长的时间和稳定的推力才能实现。

2.4 深空编队轨迹优化方法

编队航天器的应用逐渐从近地轨道向深空方向发展，并覆盖在轨服务、行星探测、引力波探测等前沿学科领域。相对于近地轨道编队飞行，深空探测编队任务的时间长、距离远、环境复杂多变，要求航天器具有更高的稳定性和可靠性。连续小推力推进系统（电推进、太阳帆等）具备推力小、比冲大等优势，被认为是执行深空飞行的优先选择。因此，小推力作用下航天器编队构建、重构以及维持的轨迹优化问题是难点之一。

文献［83-87］采用间接法和直接法等方法求解深空编队重构轨迹优化问题，但侧重点在于研究新求解方法优化计算过程或提高算法效率，对于深空编队飞行任务提出的性能指标和约束与近地轨道编队飞行较相近。因此，目前提出的技术途径对于近地轨道编队转移和重构同样适用。为了提高航天器编队重构规划与控制在深空探测力学环境下的适应能力，需要从多体系统动力学模型、航天器系统性能、深空环境约束与限制等角度出发［88］，设计更好的控制策略和预备方案［89］来应对深空环境下不确定性因素的干扰与破坏。

2.5 编队飞行轨迹优化软件求解器

本文对所调研的文献中使用的软件包进行了综述，并通过表2 对比了目前常用于编队飞行轨迹优化计算的软件求解器，具体如下表所示：

表2 常用优化求解器软件Table 2 Summary of optimization solvers

结合文献和表2 可以看出，针对多航天器的编队飞行轨迹优化问题，常用的求解器多采用直接法进行离散求解，它将能量最优或燃料最优轨迹优化问题离散为有限维的线性规划问题，通过序列二次规划法、共轭梯度法、牛顿法等求解，例如CPLEX、CVX和SNOPT等。

3 编队飞行控制的关键技术

编队航天器比单一航天器可靠性强、效率高，其应用可广泛覆盖于空间在轨服务、空间对抗、遥感和通信、天文观测、行星观测等领域。在当前多信息融合数据处理、层级控制与规划结构和拓扑通信链路等集群技术研究［90］的背景下，需发展智能群体协同操控技术［91］。随着近地轨道主动碎片清除和空间态势感知等领域的迅速发展，迫切需要建立基于相对运动的导航、制导与控制系统框架，并发展基于合作或非合作空间目标的探测、监视、绕飞和抵近等关键技术。这也是编队航天器相对运动理论应用的一个重要方向。

航天器的编队飞行任务需要解决构型设计、在轨构建与重构等任务，并且具备长期在轨的抗干扰稳定飞行能力。目前还需要在相对导航与目标感知预测技术、智能群体协同轨迹规划、编队航天器协同控制体系和拓扑结构设计与通信链路实现等方向深入研究和发展。

3.1 相对导航与目标感知预测技术

航天器相对自主导航与目标感知为后续自主规划与决策提供关键输入信息，目前需要平台具有处理多传感器信息融合的能力，使得航天器的在轨感知、预测与相对导航能够满足后续个体协调和任务规划需求。在航天器编队飞行中，个体间的相对位置估计和非合作空间目标的相对位置预测通常依赖高精度相对运动模型。此外，考虑到传感器、行星轨道环境和深空环境的不确定性和动态性，导航误差可能在航天器轨道转移和重构等过程中引入未知的风险，包括但不限于轨道偏移、不稳定性、碰撞风险或任务执行失败等，所以需要提升平台多源信息融合的能力，最大程度地减小误差。因此在编队航天器相对自主导航与目标感知技术研究中，需要综合考虑以上因素，以实现更可靠和精确的导航和控制。

3.2 智能群体协同轨迹规划

群体智能技术是编队航天器实现自组织性、协作性、稳定性、灵活性和对环境适应性的关键技术之一。目前的研究大多基于群体来建立优化模型，然而，仍存在一个重要问题，即个体行为与群体行为之间关系的考量。特别是在编队航天器中，由于不同的平台参数（如质量和推力大小）的差异，个体航天器的行为对整个编队的性能和效能具有重要影响。因此，需要深入研究个体行为与群体行为之间的相互关系，构建多级优化结构或多目标优化模型来满足个体的需求，以优化整个编队系统的构建与重构结果，使个体能够根据群体行为做出适应性调整，实现整体性能的最大化。

同时，在轨迹规划问题中尤其需要考虑转移中的防碰撞问题，碰撞约束是编队飞行轨迹规划中最难以处理的一项约束。未来实际在轨飞行任务要求升级，编队航天器的数量逐渐增多，伴随着日益严峻的空间碎片环境，轨迹优化问题求解难度呈指数级增加。因此，需要考虑航天器之间、航天器与碎片之间的防碰撞条件，研究如何减小该非线性约束条件下的轨迹优化问题计算量。

3.3 编队航天器协同控制体系

发展高鲁棒性和稳定性的协同控制方法是编队航天器走向智能化、自主化的关键。集中式控制方法对主航天器的CPU 和通信能力有较高的要求；而分布式协同控制方法可以分散主航天器的压力，降低计算量，并具有较强的灵活性。但同时它会降低系统的稳定性，并且对星间信息交互与多信息融合数据处理的依赖较高。因此，需发展应对外部干扰的变结构控制模式，这种方法能够根据系统的不确定性，及时切换适应性高的控制策略，提升编队体系的鲁棒性和稳定性。例如基于机器学习的控制框架，通过学习和自适应来适应外部干扰的变化，进一步提高编队系统的控制性能和鲁棒性。

3.4 拓扑结构设计与通信链路实现

在执行空间飞行任务时，编队航天器通常由主航天器计算和控制其他航天器的轨道机动。智能化的变结构控制要求通信有重组网的能力。这种情况下，面对不同航天器间通信链路的限制，需要重新设计拓扑编队构型，以使编队航天器能够自主优化分配构型，以弥补通信链路缺失的问题。拓扑优化的目标是使得编队中的航天器能够通过最少的通信链路实现信息传递和协同控制。通过重新设计和优化编队的拓扑结构，可以降低通信链路的需求，提高系统的鲁棒性和稳定性。此外，编队航天器需要具备自主调整编队构型能力，确保信息的可靠传递和控制的高效执行。这样的自主优化分配构型方法可以帮助编队航天器在面对通信链路缺失时也能够响应并作出调整。

4 编队飞行研究未来发展趋势

随着微小航天器搭载计算机的快速发展以及大型编队自主控制能力的提高，使航天器在向自主规划、自主计算和控制的方向发展，以提高编队系统的实时响应、自适应性、精确性和鲁棒性等。考虑到这些因素，未来编队飞行研究应在复杂环境下的编队航天器动态规划、空间非合作目标编队飞行、航天器编队飞行智能操控技术、深空探测自主编队研究与应用和平台工程应用能力提升等方面进行，更大程度地发挥航天器编队飞行优势。

4.1 复杂环境下的编队航天器动态规划

在进行空间任务时，编队航天器面临着各种复杂的情况和变化，例如目标位置的变动、环境条件的变化以及其他航天器的行为。为了应对这些变化并实现任务目标，编队航天器个体需要及时根据实时输入的信息进行调整和规划。这种动态响应和在线规划的能力对于编队航天器能否成功执行任务至关重要。通过实时信息的输入，编队航天器能够感知和理解任务环境的变化，并及时做出相应的决策和调整。根据不同的任务需求，编队航天器可以根据实时输入的信息进行路径规划、姿态调整、速度控制等操作，以确保任务的顺利进行。这样的动态响应和在线规划能力不仅可以提高编队航天器的控制性能，还可以增加任务的灵活性和可靠性。

4.2 空间非合作目标编队飞行

编队航天器对非合作目标的绕飞、抵近等技术在空间对抗领域引起了广泛的关注。这些技术的应用范围非常广泛，包括对机动和无机动的非合作目标进行跟飞、绕飞、抵近和实时监测等行动，以及推动太空资源探测等领域的发展。然而要实现这种侦察手段，就必须考虑复杂的实际约束条件和优化目标，制定航天器协同飞行和博弈对抗的控制策略。同时通过合理分配任务和资源，充分发挥编队航天器在空间对抗中的能力，以应对不同的场景和情况，实现对非合作目标的精准侦察。

4.3 航天器编队飞行智能操控技术

随着编队飞行技术的不断成熟和发展，人工智能方法在智能操控方面的应用逐渐成为一种重要趋势。通过智能学习等方法，可以进行环境交互、学习和决策，从而在一定程度上简化物理模型、减少计算量，并提高运行效率。由于智能系统可以根据实时信息进行更新和调整，它可以更好地适应环境的变化和不确定性。通过从大量的样本中学习，系统可以逐步优化决策策略，提高编队飞行的效率和性能。未来的研究和发展应该进一步探索智能学习在编队飞行中自主管理与控制的应用，以实现更高水平的智能化飞行。

4.4 深空探测自主编队研究与应用

深空探测是国家未来航天发展的主要方向之一，编队飞行在深空探测方面涉及太空望远镜、太阳系行星观测等应用，目前深空编队飞行研究在动力学模型、构型设计和控制等方面较为薄弱。因此未来应进一步细化区分不同的深空编队动力学环境，确保编队航天器在深空环境下安全可靠运行，并发展智能、自主化操控技术，形成自主远航能力。考虑深空环境特殊性与优势，研究利用太阳光压以及行星借力等外部输入控制的轨迹优化问题，可以极大拓展航天器远航能力。

4.5 平台工程应用能力提升

提升平台工程应用能力，以确保编队航天器在面对不确定因素时能够持续稳定地工作，是一个必然要求。在编队航天器的轨道飞行过程中，可能会遇到单个航天器失效、推力欠驱动等问题。为了应对这些问题，平台需要具备及时响应和系统方案制定的能力。面对单个航天器失效、推力欠驱动等问题，平台需要迅速做出响应并提供适当的解决方案。这可能涉及到飞行控制、系统重配、任务重新规划等方面。平台应该能够快速诊断问题，并通过优化的控制策略来保证编队航天器的稳定工作。在提升平台工程应用能力的过程中，还需要考虑到编队飞行航天器对星间通信能力的高要求。为了实现有效的通信和协同操作，平台需要设计合适的耦合通信链路结构，并进行优化和控制。这将有助于提高编队航天器之间的通信效率和协同能力。

5 结束语

航天器编队飞行作为现代集群的一种方式，经过多年的发展逐步实现了技术验证，美国和欧洲分别计划在未来十年内发射十几个由微小航天器组成的不同编队。本文主要关注航天器编队飞行构建、在轨重构的背景与应用，从不同的空间环境和求解方法剖析相对动力学模型，阐述编队相对运动的轨迹优化方法。本文提出，轨迹优化求解方法具有多样性，其计算效率直接影响航天器在轨飞行的操控性。

为了应对更加复杂的空间任务，实现更加灵活、自主、智能的编队飞行操控，需要重点突破相对导航与目标感知预测技术、智能群体协同轨迹规划、编队航天器协同控制体系和拓扑结构设计与通信链路实现等问题。最后探讨了未来值得深入研究的技术和发展方向，在研究过程中从实际应用需求出发，充分开展理论研究和地面仿真试验，为我国航天器在轨编队飞行奠定基础。