建模方式对调车冲击仿真的影响研究*

孙林平 杨忠良,2† 马卫华 罗世辉 王波

(1. 西南交通大学 轨道交通运载系统全国重点实验室, 成都 610031)

(2. 中国国家铁路集团有限公司,机辆部 北京 100844)

引言

随着重载铁路的快速发展,列车编组数量和轴重逐步加大,车辆之间的纵向冲击作用越来越明显[1],这对货运列车运行安全性产生不利影响,同时对列车调车编组效率也提出了更高的要求.调车冲击是利用编组车辆以一定速度冲击另一编组车辆,从而实现列车的快速编组,是车辆纵向冲击中受力最恶劣工况,易导致车辆结构的破坏[2],因此研究不同轴重、不同速度、不同编组方式等工况的调车冲击特性工作很有必要,而开展不同建模方式的数值模拟模型则对调车冲击过程的计算效率及冲击特性结果有着重要的意义.

关于车辆调车冲击碰撞的相关研究中,张锁怀[3]建立了地铁编组列车连挂冲击的非线性模型,分析了不同编组工况下车辆冲击特性,表明冲击面上的缓冲器冲击力和压缩行程都为最大.Sun[4]则建立了澳大利亚典型的旅客列车冲击模型,分析了不同编组方式及冲击速度等工况下的碰撞力.孙树磊[5]编制了MT-2缓冲器的修正模型,建立了三维车辆冲击模型,分析了不同速度及其空重车状态下的车辆冲击动态特性及其对摇枕横向载荷的影响,并通过试验对结果进行了验证.吴启凡[6]建立了参数化列车碰撞平台,将其与有限元仿真结果在速度、加速度及其轮对抬升量等方面进行对比,误差能控制在10%以内.梁朝纬[7]基于一维纵向碰撞平台,分析了不同编组长度的碰撞响应,表明主动车长度大于被动车长度时,吸收能量减小导致危险程度增加.Olshevskiy[8]建立了摩擦式缓冲器的动态模型,分析了不同编组冲击工况下缓冲器扰度变化及车钩力时间历程.Prabhakaran等[9]采用6种不同类型的缓冲器组合进行了铁路罐车冲击试验分析,得到了不同试验环境下的车辆冲击性能,表明缓冲器在减小车辆冲击力方面是有效的.Cole[10]建立了不同类型的摩擦缓冲器数学模型,得到了车辆纵向冲击动态响应及讨论了缓冲器的疲劳损伤问题.Lei[11]和刘嘉[12]等列举了缓冲器的查表法和斜楔弹簧模型法两种建模方式,分析了在调车冲击、落锤实验及其台架实验等冲击工况下的不同缓冲器建模方式对车辆冲击结果的影响.Zhou等[13]进行了缓冲器力学模型中过渡曲线的不同过渡策略的分析,建议采用中间斜率法和平滑近似方法可解决缓冲器建模时的不连续问题.

上述研究中侧重于车辆的冲击速度、质量、编组方式及缓冲器相关参数变化时的车辆纵向冲击特性,虽然文献[14]和文献[15]涉及车辆冲击不同模型之间的车钩力比较,但未对建模方式差异对冲击结果影响展开详细的定量分析.本文以重载货车调车作业为研究对象,通过建立不同的调车冲击模型,对比不同速度、空重车状态、不同编组方式等工况下调车冲击的结果,从计算时间成本、建模方便性和结果大小差异等方面进行分析,可在调车冲击仿真过程中的模型建模方面起到一定的指导作用.

1 调车冲击动力学模型

1.1 纵向动力学模型(model A)

在调车冲击过程中,将单个车辆考虑为纵向振动的质量块,车辆之间通过两个缓冲器进行串联而成,则调车冲击过程的非线性弹簧阻尼系统如图1所示,得到纵向冲击微分方程组:

图1 调车冲击模型Fig.1 Shunting impact model

(1)

式中:n-车辆总数;

mi-第i辆的质量;

xi-第i辆车的位移;

Fci-第i辆车缓冲器传递的车钩力;

Fai-第i辆车运行的阻力.

式(1)中的货车重车运行阻力Fai[16]:

货运空车阻力:

(2)

货运重车阻力:

(3)

缓冲器是消耗列车纵向冲击能量的关键性部件,能减小车辆之间的纵向冲击作用.MT-2摩擦式缓冲器是我国重载列车应用较广泛的缓冲器,具有结构简单、生产成本低、可靠性强等优点.MT-2摩擦式缓冲器的阻抗特性曲线如图2所示,可根据落锤实验或者调车冲击试验得到,多段线缓冲器的阻抗力计算可表示为[17]:

图2 MT-2缓冲器多段线性模型Fig.2 Multi-segment linear model of MT-2 buffer

(4)

式中:Fr-缓冲器阻抗力;

F0-缓冲器加载初压力(当间隙小于初始车钩间隙x0);

xt-缓冲器压缩量;

vt-缓冲器当前变形速度;

sj-缓冲器分段点横坐标;

ki-加载分段函数刚度;

F1-缓冲器卸载初压力;

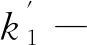
xt-Δt-缓冲器前一步压缩量;

vt-Δt-缓冲器前一步变形速度;

kg-过渡特性刚度.

式(1)中车钩力Fci与式(4)缓冲器的阻抗力 有所不同,其中车钩力有正负,与车辆相对位移有关,且在两节车厢之间为2个缓冲器的串联,定义车钩力压缩为负值,缓冲器行程压缩为负值,则车钩力与缓冲器位移之间的关系可描述为:

(5)

式中:xj-车钩间隙.

根据上述纵向冲击模型及缓冲器模型,西南交通大学牵引动力国家实验室自主研发了列车纵向动力学及能量仿真分析软件(TDEAS)[18],软件部分界面如图3所示,界面需设置编组方式、车辆参数、缓冲器参数、线路参数、操控方式及后处理参数,可实现无限长度编组的列车纵向动力学与能耗仿真.TDEAS软件的模型及算法通过试验线路进行了论证,同时参与了国际测评[19],与国际平台的纵向动力学软件进行对比分析,得到了国际基准测试列车纵向动力学仿真器的认证.

图3 TDEAS软件Fig.3 Software of TDEAS

1.2 三维精细化模型(model B)

将钩缓装置模型简化如图4所示,主要参数如表1所示,动力学模型共有前、后半车钩两个物体组成(总长为车钩名义长度),车钩相对车体可以伸缩(x方向平移)和绕铅垂(z)、横向水平(y)向转动,在前后半车钩之间考虑了缓冲器的间隙,同时在前、后车钩与车体之间考虑了图2中MT-2缓冲器的加载与卸载动态非线性特性.

表1 货车动力学模型主要参数

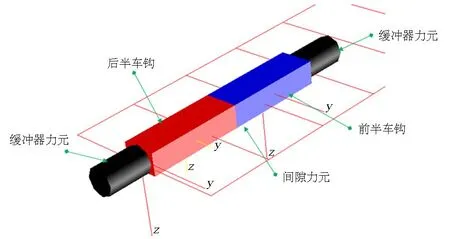
图4 简化钩缓模型Fig.4 Simplified hook buffer model

同时采用SIMPACK软件建立货车完整多体动力学模型,包含了车体、心盘、摇枕、侧架、轮对以及轴箱装置[20,21],货车动力学参数如表1所示.将单节货车完整动力学模型(图4)与简化的钩缓模型通过子模型结构进行编组,形成如图5所示的三维精细化模型[15].

图5 三维精细化动力学模型Fig.5 3D refined dynamics model

1.3 混合动力学模型(model C)

混合动力学模型是指将一维模型和三维精细化模型混合建模的一种方式,如图6所示,其中一维模型是指去除精细化模型(图5)中部分车辆的悬挂及其轮轨系统,将其考虑为单个质量块,从而形成混合动力学模型[22].为了尽可能地简化系统自由度考虑,此次模型分析中只保留在冲击面后的一个三维精细化车辆模型,其余车辆全部均考虑为单个质量块.

图6 混合动力学模型Fig.6 Hybrid dynamics model

2 仿真结果对比分析

为了分析上述模型在不同工况下计算结果的差异,以已经得到国际基准认证的TDEAS软件(model A)的结果为基准,对比多体动力学软件中建立的三维精细化模型(model B)和混合动力学模型(model C)与纵向动力学模型(model A)在不同速度、空重车状态、不同编组方式下计算结果的差异.

2.1 不同速度对比

以1辆重车冲击1辆重车(记为:1V1,后文编组方式类似标记)为例进行分析不同速度冲击时的最大车钩力如图7所示,几种模型的最大车钩力随着速度增加而增加,同一速度下模型A的车钩力最大,模型B与模型C接近;在速度小于6.5km/h时几种模型的差值较小,大于6.5km/h之后,模型A和模型B之间最大车钩力随着速度的增加,差值也越来越大,在冲击速度8km/h时差距达到了15%左右,略小于文献[14]中分析的21.7%.

图7 不同速度时的最大车钩力Fig.7 Maximum coupler force at different speeds

2.2 空重车状态对比

1V1在速度6km/h冲击时空重车状态下最大车钩力如图8所示,可知重车冲击相比空车冲击的最大车钩力偏大,这是因为质量的增加,相对惯性越大导致的;同时重车之间冲击时模型B与模型A之间的车钩力差异为2.4%,模型C与模型A的差异为1.2%,空车相互冲击时模型B与模型A之间的车钩力差异为8.9%,模型C与模型A的差异为7.4%,空车之间冲击结果比重车冲击结果差异稍偏大.

图8 空/重车状态下最大车钩力Fig.8 Maximum coupler force under empty/heavy vehicle condition

2.3 不同编组方式对比

以不同编组方式(2V2,3V3)4km/h冲击时的冲击面车钩力历程如图9所示,对比冲击面车钩力时间历程可知三种模型变化趋势相同,在冲击面上的车钩力均在初始时刻存在多个波峰,这是因为在初始撞击之后,后续车辆的相互作用力导致冲击面缓冲器的再次压缩形成的,其后的车钩力的衰减震荡是因为车辆之间经历多次相互作用及其缓冲器的耗能导致的,且都在初次碰撞瞬时达到最大,其后缓慢衰减.

图9 不同编组的车钩力时间历程Fig.9 Time history of coupler force in different groups

不同车钩位的最大车钩力分布如图10所示,最大车钩力分布规律也较为类似,即在冲击面上的车钩力最大,沿着冲击面前后递减,不同车钩位置之间的最大差异如表2所示,可知冲击面最大差异为3V3时模型C与模型A的8.8%.

表2 不同车钩位置的差异(%)

图10 不同编组的最大车钩力分布Fig.10 Maximum coupler force distribution of different groups

2.4 建模方便性及计算时间分析

从计算结果对比分析:几种模型的计算结果从不同速度、空重车状态、不同编组分析的结果整体变化规律较为类似,其数值上有一定的差距,在实际允许的最大调车速度5km/h[23]时的差异范围都在10%以内,几种模型计算结果相似程度可达90%以上.

从建模方便性、适用性上对比分析:模型A中不需考虑转向架,可以很快实现任意车型的建模,且在TDEAS软件中可以实现任意车辆编组长度,但重难点在于数据库的建立,而一旦建成数据库,便可以在后续分析中无限次调用,只需在图3的软件界面中输入车辆数量即可;模型B针对具体转向架需要重新建模,通用性较差,编组车辆建模时可采用子模型技术实现,但系统自由度较多,建模较为复杂;模型C可以一定程度上缩减模型B的自由度,但仍然不能避免建模复杂的问题.

几种模型在电脑配置相同的条件进行不同编组调车冲击所需分析时间如表3所示,从表中可知模型A分析的时间远远小于其他两种模型,同时模型C的计算时间比模型B也节约了不少,平均时间节约了近43%,完全精细化模型B在车辆3V3时的分析时间已经超过5000s,如果再继续增加车辆数量,相应的仿真计算时间将会大幅增加.

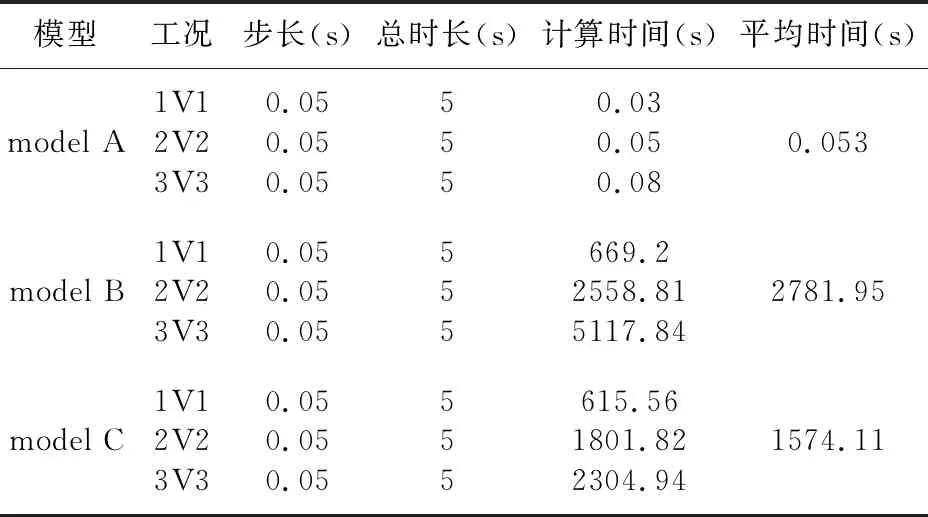
表3 不同模型计算时间

3 结论

本文针对调车非稳态冲击过程建立了三种仿真模型,在不同速度、空重车状态及不同编组方式等工况进行了仿真模型之间的计算效率和结果对比,得出以下结论:

(1)纵向动力学模型、三维精细化模型及其混合动力学模型等在实际允许的调车速度内分析的车钩力计算结果误差在10%以内.

(2)三种仿真模型在建模方式上都有较为复杂性,但纵向动力学模型中建立的车辆信息数据库在软件界面调用时更为方便,且计算时间最快.