结合灵敏度分析的圆锥壳-折板结构动力学研究*
章海亮 胡阳鸣 罗伟峰,† 戴宏亮 邓勤 朱振涛 邓劭廷 胡飞
(1. 湖南云箭集团有限公司,长沙 410100)
(2. 湖南大学 机械与运载工程学院,长沙 410082)
(3. 北京宇航系统工程研究所,北京 100076)
引言
随着航空技术朝着“高精尖”方向发展,航空装备需在舱体内搭载各种不同用途的科学仪器设备,使航空装备舱体结构逐渐趋向于大型化、复杂化与多功能化.作为航空装备重大核心精密科学仪器设备的承载体,舱体结构强度设计问题尤为关键,目标对象定位意义重大.圆锥壳-折板结构在舱体结构中十分常见,其动力学特性研究十分重要.高空飞行器悬挂物舱体结构在工作过程中结构极易发生振动,长此以往便容易使其产生疲劳损伤,甚至发生断裂,这将导致极大的安全隐患.随着航空装备的设计要求提高,各种因素对舱体动强度的影响越来越受到重视.因此,有必要研究杂弹体结构动强度影响因素,并且探究其影响规律.
不同结构之间存在能量的传递和流动,导致组合结构的动力响应复杂.因此,不少学者对这种组合结构的振动特性进行了研究.基于变分原理,Cheng等[1]研究了末端耦合圆板的有限长圆柱壳的自由振动.采用瑞利-里兹方法,Chen等[2]建立了圆柱壳板耦合结构的数值模型,计算了耦合结构的能量流和振动行为.邹明松等[3]半解析地求解了两端具有端板的圆柱壳结构的自由振动问题.基于板-壳耦合结构处的连续性条件,李鸿秋[4]建立了一般连接形式下板-壳耦合结构分析模型,并且验证了该模型耦合结构动力学特性的正确性.基于谱几何法,石先杰等[5]构建了热环境下FGM圆锥壳振动的半解析分析模型,并研究了不同因素的影响规律.在改进的傅立叶-里兹方法的理论框架内,Ma等[6]求解了具有一般边界条件的圆柱壳-环形板耦合结构的振动行为.Xie等[7]在波基法的基础上,研究了弹性边界条件下含弹性耦合环形薄板圆柱壳的自由稳态振动行为.基于一种改进的傅立叶级数方法,Cao等[8]求解了不同边界条件下圆柱壳-圆板耦合结构的振动行为.Chen等[9]结合了Flügge薄壳理论和波的方法,分析了具有内部结构有限长圆柱壳的振动行为.Qin等[10]利用Mindlin板理论和Sanders壳理论,得到了平板和壳的能量方程,研究了旋转圆柱壳-环形板耦合结构的振动特性.采用最小二乘复频域法,李旭龙等[11]对对接圆柱壳结构进行了计算模态分析和实验模态分析.基于Donnell薄壳理论,韩勤锴等[12]采用多尺度方法研究了变速旋转圆柱薄壳动力稳定性.迄今为止,国内外相关研究绝大多数都是对针对圆柱壳及其耦合结构展开的,圆锥壳耦合结构的相关研究较少.
本文以圆锥壳-折板结构为对象,对其动力学特性展开分析.通过仿真计算,得到圆锥壳-折板结构在随机振动下的响应结果.经过计算得到不同结构下多个样本值,并且利用其建立材料参数与动力学响应之间的响应面函数.基于上一步得到的响应面函数模型,进一步利用Spearman秩相关系数,进行灵敏度分析,筛选出圆锥壳-折板结构中影响舱体结构动强度的主要因素.最后,利用参数化模型开展参数影响规律研究,得到各个主要因素对于响应面动力学响应的影响规律曲线.
1 理论模型的建立
1.1 动力学方程
典型舱体结构主要分为两个部分:尾舱以及安装座.尾舱几何外形为厚圆锥壳,安装座几何外形为对称四折板结构,舱体几何结构如图1所示.

图1 圆锥壳-折板耦合舱体结构Fig.1 Cylindrical-conical shell coupled with folded plate
动载荷下舱体结构的整体动力学方程为
(1)
其中:M为质量矩阵,D为阻尼矩阵,K为刚度矩阵,F(t)为激励振动载荷向量,X为广义位移向量.
由动力学方程可得结构的频域运动方程,表示为
(K-ω2M)X=F(t)
(2)
其中:ω为激振频率.
用于求解结构模态振型的特征方程可表达为
(3)
其中:ωi为第i阶固有频率,Ai为第i阶实模态振型.
结构复频响函数矩阵为
(4)
结构模型可认为是小阻尼系统,可认为引入的阻尼并不影响系统的特征向量,因而可用实模态理论分析系统振动行为.
利用求得的模态振型矩阵A,对上述方程做正交变换有
=A[K-ω2M]-1AT
(5)
式中ηi为由阻尼部分产生的第i阶模态损耗因子.
节点响应为
S(ω)=|H(ω)|Sx(ω)
(6)
其中:Sx(ω)为激励载荷功率谱密度函数,S(ω)为响应功率密度谱.
1.2 灵敏度分析理论
建立材料参数与响应参数之间的响应面函数:
(7)
式中:xi为自变量,数量为N;y为动力学响应;a、ai与aij(i=1,2,…,N;j=i,i+1,…,N)均为待定系数.
对L个样本点进行数值模拟,得到L个响应结果(z1,z2,…,zL).结合二阶响应面函数进行回归分析得
(8)
令
(9)
对其进行求解,从而确定待定系数a、ai与aij(i=1,2,…,N;j=i,i+1,…,N)的值.
确定响应面函数后,以材料参数q为自变量输入,结构响应p为输出,计算n个样本,得到n个数据对:
(10)
将一组数据对转化成等级数据
(11)
式中R(qi)和R(pi)分别是qi和pi的位次.
Spearman相关系数ρ为

(12)
Spearman相关系数ρ反映了结构响应p与材料参数q之间的相关性:相关系数ρ为正,说明结构响应p随材料参数q的增加而增加,两者呈正相关关系;反之相反.而|ρ|的大小反映了结构响应p与材料参数q之间相关的显著程度.|ρ|越大,表示材料参数q的变化对于结构响应p的影响越显著,即结构响应p对于材料参数q越敏感.本文以Spearman相关系数ρ作为灵敏度判断指标,文章中后续出现的相关系数均代指Spearman相关系数.
2 灵敏度分析算例
为了研究圆锥壳-折板结构的动力学特性,结构尺寸如下:尾舱几何外形为厚圆锥壳,顶端外径为315mm,底端外径为410mm,高705mm.安装座几何外形为对称四折板结构,板厚2mm且厚度均匀,顶面为180mm×120mm的方形,肋板高70mm,两侧座脚均为120mm×13mm的方形.载荷输入位置与响应输出位置如图1所示.
灵敏度分析时各参数变化范围为±10%,具体数值如表1所示.

表1 灵敏度分析材料参数变化范围
输入载荷的激励类型为随机振动,随机振动是由无数正弦波构成,用通过在中心频率设置的窄幅过滤器的加速度信号平方的平均值的单位频率值表示,即功率谱密度.载荷输入位置如图1所示,输入载荷功率谱密度如图2所示.

图2 载荷功率谱Fig.2 Spectral density of load
由图3可知,尾舱材料密度与变形响应和应力响应均呈现正相关关系,且相关系数较大,分别为0.29与0.36.尾舱材料杨氏模量与变形响应和应力响应均呈现负相关关系,且相关系数较大,分别为-0.33和-0.37.安装座材料密度与变形响应呈现负相关关系,且相关系数较大,为-0.18.安装座材料杨氏模量与应力响应呈现正相关关系,且相关系数较大,为0.59.

图3 不同响应对各参数灵敏度对比Fig.3 Comparison of the sensitivity of different responses to each parameter
3 主要参数的影响规律研究
各参数与位移变形响应的相关曲线如图4所示.

图4 各参数与位移响应间相关曲线Fig.4 The correlated curves between each parameter and the displacement response
由图4(a)可知,尾舱材料密度与位移变形响应整体呈现出正相关关系,随着密度的增大变形响应逐渐增大,同时曲线斜率逐渐增大,位移变形增大的趋势逐渐加强.在尾舱材料密度低于2500kg/m3后,位移变形响应变化不再明显.尾舱材料密度越低,杨氏模量变化带来的位移变形响应变化越小.
由图4(b)可知,尾舱材料杨氏模量与位移变形响应整体呈现出负相关关系,随着材料杨氏模量的增大变形响应逐渐减小,同时曲线斜率逐渐变小,位移变形减小的趋势逐渐减缓.在尾舱材料杨氏模量超过75GPa后,位移变形响应变化不再明显.尾舱材料杨氏模量越高,密度变化带来的位移变形响应变化越小.
各参数与应力响应的相关曲线如图5所示.

图5 各参数与应力响应间相关曲线Fig.5 The correlated curves between each parameter and the stress response
由图5(a)可知,尾舱材料密度与应力响应整体呈现出正相关关系,随着材料密度的增大应力响应逐渐增大,同时曲线斜率逐渐增大,应力增大的趋势逐渐提高.尾舱材料密度越低,杨氏模量变化带来的应力响应变化越小.
由图5(b)可知,尾舱材料杨氏模量与应力响应整体呈现出负相关关系,随着材料杨氏模量的增大应力响应逐渐减小.尾舱材料杨氏模量越高,密度变化带来的应力响应变化越小.
由图5(c)可知,安装座材料杨氏模量与应力响应整体呈现出正相关关系,随着材料杨氏模量的增大应力响应逐渐增大,同时曲线斜率逐渐增大,应力增大的趋势逐渐提高.安装座材料杨氏模量越低,密度变化带来的平均应力响应变化越小.
各参数与加速度响应的相关曲线如图6所示.
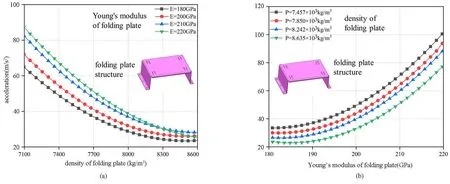
图6 各参数与加速度响应间相关曲线Fig.6 The correlated curves between each parameter and the acceleration response
由图6(a)可知,安装座材料密度与加速度响应整体呈现出负相关关系,随着安装座材料密度的增大加速度响应逐渐减小,同时曲线斜率逐渐变小,加速度减小的趋势逐渐减缓.在安装座材料密度超过8300kg/m3后,加速度响应变化不再明显.尾舱材料密度越高,杨氏模量变化带来的加速度响应变化越小.
由图6(b)可知,安装座材料杨氏模量与加速度响应整体呈现出正相关关系,随着安装座材料杨氏模量的增大加速度响应逐渐增大,同时曲线斜率逐渐变大,加速度增大的趋势逐渐减缓.在安装座材料杨氏模量低于185GPa后,位移加速度响应变化不再明显.
4 结论
通过本文的研究可以得出了如下结论:
(1)以圆锥壳-折板结构模型为基础,进行了随机振动下的结构动力学分析,得到了结构的位移、应力以及加速度响应.
(2)通过基于响应面法和Spearman秩相关系数的灵敏度分析,分析影响圆锥壳-折板结构动强度的主要因素.结果表明:对于圆锥壳-折板结构,位移变形响应受圆锥壳密度与杨氏模量影响最为明显,其灵敏度相关系数分别为0.29和-0.33;应力响应受圆锥壳材料密度与杨氏模量以及折板材料杨氏模量影响十分明显,其中折板材料杨氏模量影响最为显著,其灵敏度相关系数分别为0.36、-0.37和0.59;加速度响应受折板材料密度与杨氏模量影响较为明显,其灵敏度相关系数分别为-0.37和0.38.
(3)利用参数化模型开展参数影响规律研究,得到各个主要因素对于结构动力学响应的影响规律曲线.

