一种在轨可展开天线的多柔体动力学建模与计算*

朱文璁 宋晓东 单明贺 田强

(北京理工大学 宇航学院,北京 100081)

引言

随着航天事业的发展与航天任务日趋复杂化,百米至千米量级尺寸的大口径望远镜[1-3]、大型天线[4-6]、空间太阳能阵列[7-10]和太阳帆航天器[11,12]等大型空间系统将被用于如高精度观测、大容量通信、空间太阳能电站、深空探测等更加复杂的航天任务.这些新型航天器往往需要通过多次发射并且通过在轨展开与组装的方式完成建造.这类结构具有极低的低阶固有频率、需要长时间在轨工作等特点,为航天器动力学建模与计算问题提出了新的要求.主要包括:准确描述复杂空间环境作用下柔性体大范围运动和大变形耦合的建模方法,以及长时间保持系统能量的时间积分算法等.

针对上述需求,近年来在空间结构展开动力学领域已经有了很多研究进展.Li[13]建立了环形桁架天线的展开动力学模型,通过五次多项式规划的方式模拟了天线的平稳展开.Yu等[14]采用绝对节点坐标缩减梁单元对空间索杆式伸展臂建模,研究了构件碰撞对展开动力学的影响.Liu等[15]基于能量等效原理和铁木辛柯梁理论建立了具有初应力的空间天线桁架等效动力学模型,分析了天线桁架的固有频率和固有模态.Otsuka等[16]采用绝对节点坐标板单元对卫星太阳能电池板展开系统建模,研究了复合旋转角和闭锁机构扭矩对结构展开的影响.除展开动力学分析外,重力梯度等复杂空间环境对大型空间结构动力学响应的影响也是相关领域的研究热点之一.Mcanlly等[17]分析了轨道半径、初始姿态等参数对重力梯度作用下的哑铃模型动力学响应的影响.Ishimura等[18]使用柔性哑铃模型建立了绳系空间太阳能电站模型,分析系统固有频率对轨道、姿态和振动耦合的影响.Woo等[19]分析了带有可动质点的长系留系统质心和轨道中心的区别,研究了质点运动对结构姿态的影响.Mally等[20]考虑地球扁率和日月引力,研究了地球同步Laplace轨道上运行的空间太阳能电站的轨道动力学特性.Liu等[21]使用浮动坐标法建立了空间太阳能电站模型,研究了重力梯度导致的轨道-姿态耦合效应.穆瑞楠等[22]将空间太阳能电站简化为柔性梁模型,使用浮动坐标法分析了姿态、轨道与振动相互耦合时系统的稳定性.魏乙等[23]基于体积积分重力势能和绝对节点坐标方法研究了绳系空间太阳能电站的动力学响应.Li等[24]提出了一种适用于绝对节点坐标单元的重力计算方法,该方法能够简洁地表示单元受到的重力梯度及其Jacobi矩阵.Li等[25]还推导了自然坐标单元重力梯度表达式,研究了空间太阳能电站的多刚体模型在重力梯度和太阳光压作用下的动力学响应,并设计了姿态控制系统进行仿真.目前文献中未见考虑重力梯度作用的大型空间柔性结构的展开动力学研究.为此,本文在结构展开过程中考虑了重力梯度的影响,能够更精确地计算结构展开过程中的动力学响应.

求解柔性多体系统动力学方程的算法包括Newmark算法、广义α算法等方法.但是这些算法存在高频耗散和数值不稳定现象,无法在长时间的计算中保持系统能量、动量等基本物理量.因此,很多学者研究了能够长时间保持能量、动量等系统基本性质的数值积分算法.Hughes等[26]在α类方法的基础上通过引入约束方程与Lagrange乘子强制使能量保持不变,提出了强制守恒方法.但是这种方法没有考虑算法的数值耗散,会导致系统高频模态的能量向低频模态转移.另一类常见的用于计算空间结构长时间在轨的动力学问题的算法是辛Runge-Kutta方法.邓子辰等[27]将辛Runge-Kutta算法应用到太阳帆塔的动力学响应问题计算中,对结构进行了稳定性分析,实现了长时间计算的能量守恒.Li等[28]提出了基于一般Runge-Kutta格式的保能量保约束算法,分析了刚体空间结构的轨道-姿态耦合动力学响应.彭海军等[29]提出一种辛自适应非线性最优控制算法,研究了航天器的最优轨道转移问题.但是辛Runge-Kutta算法在计算中需要同时迭代广义动量和广义坐标,计算速度相对较慢.相比之下,保能量动量时间积分算法迭代格式的Jacobi矩阵规模相对较小,需要计算资源较辛Runge-Kutta算法少,且可以同时保持系统的能量和动量,在大型空间结构长时间在轨动力学问题的计算中有广阔应用前景.

保能量动量时间积分算法最早由Simo等[30]提出用于解决非线性弹性动力学的计算问题.这种算法通过Lagrange中值定理构造中点时刻导数二阶近似来保证系统守恒特性[31],Gonzalez[32]在非线性对称哈密顿系统的研究中将这种中点导数的近似被命名为离散方向导数[32].Simo等将这种算法用于几何精确梁[33]、壳[34]结构的动力学仿真中,并实现了和保辛算法的对比[31].Bauchau等[35]最早将保能量动量时间积分算法用于多柔体系统动力学方程的计算中,研究了算法对高频振荡的保持性质.Hou等[36]基于保能量动量时间积分方法,研究了用离散弹性杆建模的绳网系统展开动力学.

本文将保能量动量时间积分算法用于在轨空间可展开结构的动力学计算.建立了空间可展开结构模块的刚柔耦合动力学模型,和商业软件ADAMS进行对比验证了建模方法的正确性.通过空间柔性梁模型的经典算例验证了保能量动量时间积分算法在大型空间结构动力学计算上的有效性,并分析了大型空间结构的在轨展开与轨道机动过程.

1 可展开空间天线桁架结构的动力学模型

1.1 动力学建模方法简述

采用基于绝对节点坐标参考节点方法[37](Absolute Nodal Coordinate Formulation Reference node,ANCF-RN)描述的刚体单元和基于绝对节点坐标方法[38](Absolute Nodal Coordinate Formulation,ANCF)描述的三维欧拉-伯努利梁单元为结构进行建模.

ANCF-RN方法描述的刚体单元的广义坐标可以表示为

(1)

其中,r为刚体单元上固定点O在全局坐标系下的位置矢量;rx,ry,rz为相互垂直,固定在刚体上的单位矢量.刚体上任意点P在全局坐标下的位置矢量rP可以表示为

rp=Ce

(2)

其中,C=[I3c1I3c2I3c3I3]为单元形函数.c1,c2,c3分别是P点在以固定点O为原点,以rx,ry,rz为基矢量的连体坐标系的三个方向上的坐标,I3为3阶单位矩阵.

ANCF方法描述的欧拉-伯努利梁单元包括2个节点,每个节点有6个自由度,单元的广义坐标表示为

(3)

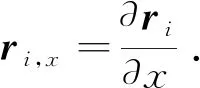
rp=Se

(4)

其中,S=[S1I3S2I3S3I3S4I3]为单元形函数矩阵;S1=1-3ξ2+2ξ3,S2=l(ξ-2ξ2+ξ3),S3=3ξ2-2ξ3,S4=l(-ξ2+ξ3),ξ=x/l,l为单元长度.将式(4)对时间求导,得到单元中任意点的速度

(5)

进一步可以得到单元的动能为

(6)

其中,ρ为单元密度,Me为单元的质量矩阵,表达式为[40]

(7)

使用ANCF方法与ANCF-RN方法为结构建模,得到系统各单元的质量矩阵、弹性力与外力.代入第一类拉格朗日方程,考虑系统约束,即可得到描述系统动力学特性的微分代数方程组

(8)

其中,M为系统质量矩阵,q为系统广义坐标,F(q)为弹性力,Q(q)为广义外力,g(q,t)为系统约束方程,gq为约束方程对广义坐标的Jacobi矩阵,λ为Lagrange乘子向量.

1.2 基于绝对坐标法表示的重力梯度

作用于空间结构上的重力梯度力矩由各部分受到的不同引力产生.根据Li等[24]的研究,万有引力可以等效为ANCF方法描述的单元节点上的广义外力.对于受地球引力影响的物体,其引力势能Ug可以表示为

(9)

其中,ρ为物体密度,V为物体体积,μ为地球引力常数,r为物体上任意点相对于地心的位置矢量.设物体质心相对于地心的位置矢量为r0,并将式(9)在r0进行泰勒展开,有[24]

(10)

对于使用ANCF方法描述的单元,单元质心的全局位置坐标矢量可以表示为

(11)

其中,m为单元质量,S为单元形函数,q为单元的广义坐标.将单元的形函数和广义坐标代入引力势能表达式并积分,有

(12)

其中

将引力势能对广义坐标分别求一阶偏导数和二阶偏导数,即得绝对节点坐标单元所受广义引力Q及其Jacobi矩阵Jg为[24]

(13)

(14)

将式(13)作为广义外力项代入微分代数方程(8)中,即可分析重力梯度对空间结构动力学响应的影响.

1.3 可展开空间天线桁架结构动力学模型

本文研究的空间天线桁架由多个外形为六棱柱的可展开模块和一个星本体在轨组装而成.每个模块框架上的柔性梁通过固定约束连接,其余部分通过旋转副连接.每个模块具有两个可通过约束互相配合的对接结构,分别编号为1、2,各自建模为刚体,用于不同模块之间的组装.可展开模块的构型如图1所示.

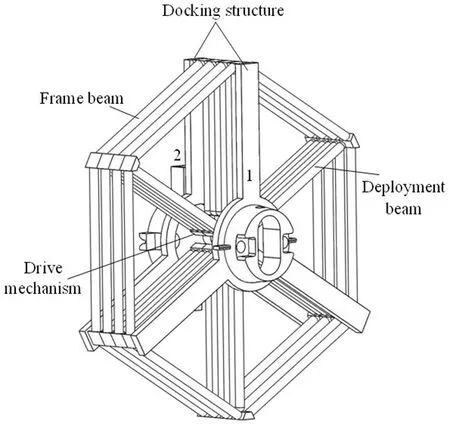
(a) 收拢构型

模型参数如表1所示.

表1 空间天线桁架结构中可展开模块的参数

在收拢状态下,展开杆与驱动机构之间夹角为0°,展开状态下驱动机构两侧的展开杆与驱动机构之间夹角各为90°.采用Flash等[41]提出的5次多项式作为角度正弦值的控制函数用于驱动模块的展开,其形式为

(15)

其中,α(t)为t时刻展开杆与驱动机构之间的夹角;tf为单个模块展开时间.

为验证建模方法的正确性,分别用本文描述的建模方法以及ADAMS与ABAQUS联合仿真的方法计算结构中单个模块展开过程中的末端位移.其中,商业软件联合仿真通过在ABAQUS中生成柔性体的模态中性文件,并将其导入到在ADAMS中建立的可展开模块刚体模型中,实现刚柔耦合模型的动力学建模与计算.结构的展开过程则分别采用如式(15)所示的角度控制函数,以及作用在展开方向上的大小不同的加速度进行驱动.此处加速度大小分别为0.1g,1g,10g,g=9.81m/s2.结构的末端位移定义为图1中所示模块的对接结构1质心位置相对于对接结构2质心位置的距离.展开过程中该点位移随时间变化的曲线如图2所示.

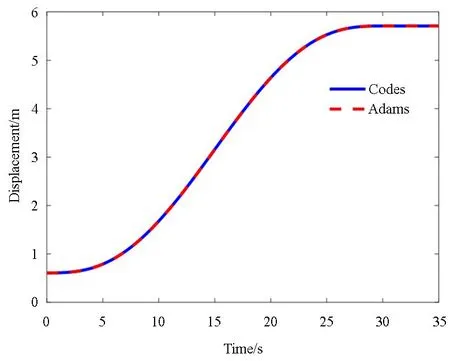
(a) 角度控制函数作用下结构展开过程中的末端位移

图2(a)的结果显示,在使用如式(14)所示的角度函数控制展开的情况下,两种方法计算的位移非常接近.图2(b)的结果显示,加速度增大导致结构内部出现更大的运动速度与柔性变形,此时两种方法计算的位移差异明显增大.和商业软件使用的传统有限元法相比,本文的建模方法在惯性系下用统一的插值函数描述刚体运动和柔性变形,更适合处理具有大变形与大转动的问题[38].

2 保能量-动量时间积分算法

对于空间结构动力学问题的计算,需要保持系统整体能量、动量等基本物理量不变.本文采用Simo等[30]提出的保能量动量时间积分算法求解系统动力学方程,该算法通过离散方向导数的构造保证了系统总能量和动量的守恒[42].

2.1 保能量-动量时间积分算法迭代格式

保能量-动量时间积分算法在连续时间域[0,T]内对微分代数方程式(8)进行等时间步离散,采用Lagrange乘子法处理系统约束.特别地,保能量-动量时间积分算法通过离散方向导数[32]表示系统势能和约束方程的Jacobi矩阵.算法需要求解的离散时间域内任意相邻两时刻的广义坐标和广义速度之间的关系、系统离散化的动力学方程以及系统约束方程如式(16a)～式(16c)所示

(16a)

(16b)

g(qn+1)=0

(16c)

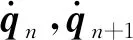
保能量-动量时间积分算法在非线性动力学方程的计算过程中需要通过牛顿迭代求解各时刻的广义坐标与Lagrange乘子.设

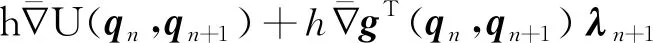
(17a)

rλ=g(qn+1)

(17b)

算法需要求解的非线性方程即为

rq=0

rλ=0

(18)

在牛顿迭代中需要计算的线性代数方程为

(19)

其中k为系统约束方程个数.

2.2 离散方向导数

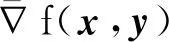
(20)

离散方向导数的表达式为

(21)

其中,∇f[(x+y)/2]为函数f(x)在(x+y)/2处对自变量的导数.如式(21)描述的表达式可以用于计算式(16)所需的离散方向导数.

将f(y)-f(x)在(x+y)/2进行Taylor展开,设v=(y-x)/2,有

(22)

将式(20)代入式(22)中,点乘v的正交向量,有

(23)

因此离散方向导数实际上是函数f(x)在x,y中点的导数的二阶近似.

3 算例研究

3.1 空间柔性梁的动力学分析

为验证保能量动量时间积分算法应用于在轨柔性空间结构动力学问题上的有效性,考虑空间柔性梁模型受重力梯度作用在椭圆轨道上运动的问题.采用和参考文献[24]中相同的算例与参数设置,同样使用ANCF方法描述的欧拉-伯努利梁单元为结构建模并将柔性梁划分10个单元.在重力梯度作用下,结构会出现明显的刚体运动和柔性变形.根据1.3节所示结果,此时能够描述结构大变形与大转动的ANCF方法相对传统有限元方法具有明显优势.模型中其他参数如表2所示.

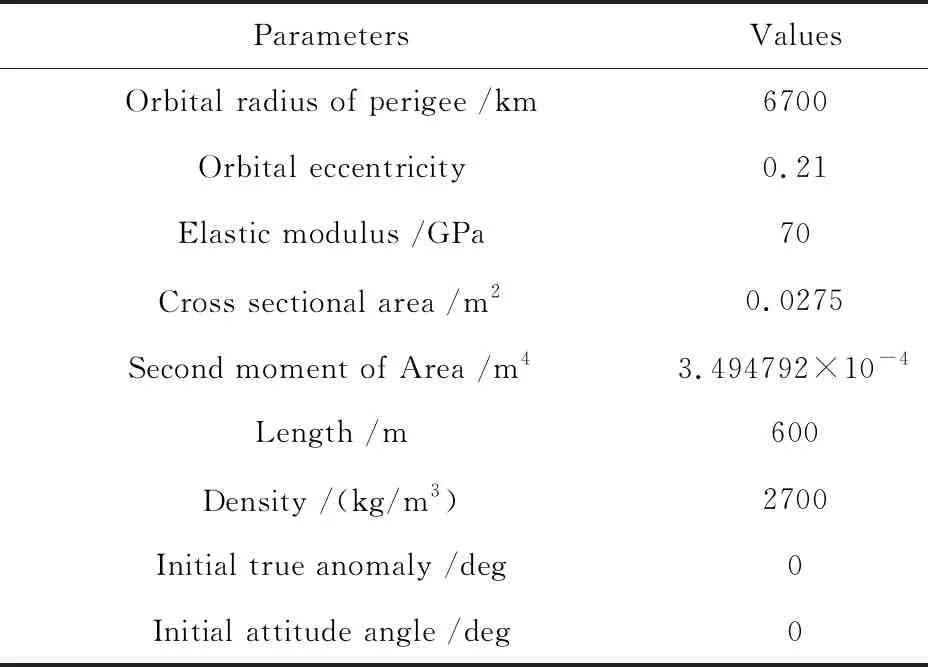
表2 空间柔性梁模型参数

空间柔性梁模型如图3所示.仅考虑柔性梁在轨道面内的运动情况,以地心O为原点建立惯性坐标系O-XY,坐标轴OX,OY在轨道平面内,OX轴指向近地点.以柔性梁质心o为原点建立结构连体坐标系o-xy,ox轴指向o点处柔性梁中性轴的切线方向,oy轴指向o点处柔性梁中性轴的法线方向.初始时刻结构位于近地点,在运动过程中始终位于轨道平面内.其中,r是连体坐标系原点o相对惯性系原点O的位置矢量;u是结构末端相对初始构型的位移矢量;r和OX轴夹角θ为真近点角;ox轴方向和r夹角φ为结构姿态角;u在ox轴上的投影ua为结构的轴向变形;u在oy轴上的投影ut为结构的横向变形.

图3 空间柔性梁模型Fig.3 The model of flexible beam in space

分别采用保能量动量时间积分算法和广义α算法计算结构的动力学响应.其中广义α算法的谱半径选取为1;保能量动量时间积分算法直接求解动力学方程组.两种算法的时间步长取5×10-4min.图4给出了两种算法计算的空间柔性梁模型在公转5个周期内的动力学响应,包括系统相对能量误差、结构姿态角、轴向变形与横向变形.其中,设初始时刻系统能量为真实能量,计算过程中任意时刻系统能量和真实能量之间绝对误差与真实能量之比即为此时系统相对能量误差.用“EM method”表示保能量动量时间积分算法,“GA method”表示广义α算法.

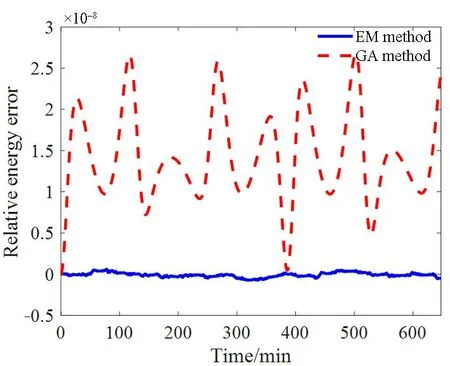
(a) 系统相对能量误差曲线

由图4(a)可知,保能量动量时间积分算法计算的系统相对能量误差比广义α算法的结果更小,具有更好的能量守恒性质.图4(b)～(d)的结果表明,两种算法计算的结构姿态运动和轴向变形的结果非常接近,但保能量动量时间积分算法计算的横向变形结果大于广义α算法的结果.本文使用的保能量动量时间积分算法对姿态角、轴向位移、横向位移三项动力学响应量的计算结果与文献[24]中Figs.10～Figs.12的结果一致.上述结果表明,柔性梁在重力梯度作用下横向变形与轴向变形具有较小的振幅和较高的频率,结构的轴向变形在姿态运动的影响下叠加了和姿态运动同频率的振动.

3.2 空间天线桁架结构在轨展开动力学分析

可展开空间天线桁架结构模型由一个建模为刚体的长方体星体和两侧各5个在1.3节中描述的展开模块组成.模型参数如表3所示.

表3 可展开空间天线桁架结构模型参数

结构展开过程如图5所示.采用角度控制函数(15)控制星体两侧的模块从中心到两端依次展开,仿真总时间设为25min.在地心O建立三维惯性坐标系O-XYZ,OX轴由地心指向结构质心初始位置,OZ轴沿地球自转轴,OY轴方向通过右手定则确定.连体坐标系o-xyz原点o位于结构质心,ox轴,oy轴,oz轴沿结构惯性主轴方向,其中ox轴沿结构的展开方向.在图5中,r是连体坐标系原点o相对惯性系原点O的位置矢量.将连体坐标系ox轴方向和r夹角φ定义为结构姿态角;将末端对接结构质心相对于星本体质心的位移矢量在ox,oy方向上的投影定义为结构运动过程中的轴向位移和横向位移.

图5 空间天线桁架结构在轨展开过程Fig.5 On orbit deployment process of the space antenna truss structure

分别采用保能量动量时间积分算法和广义α算法计算结构的动力学响应.广义α算法的谱半径取为0.8.两种算法的时间步长取5×10-4min.图6给出了两种算法计算的空间结构在轨展开过程中的动力学响应,包括结构姿态角、轴向位移与横向位移.其中,用“EM method”表示保能量动量时间积分算法,“GA method”表示广义α算法.

(a) 结构姿态角曲线

图6(a)显示,结构在展开的过程中产生了明显的姿态运动,结构姿态角即图5中的φ角最小为-30.18°.图6(b)显示,结构在每个模块展开周期内的末端轴向位移符合式(15)的规划,具有良好的稳定性.图6(c)显示,结构末端横向变形幅值在展开过程中逐渐增大,最大值为7.5×10-3m.结果表明,重力梯度对初始姿态角为90°的结构展开过程中的姿态运动存在明显影响;末端横向变形的增加反映了展开过程中结构的柔性更加显著.保能量动量时间积分算法和广义α算法对空间结构展开过程动力学响应的计算结果差别不大.

3.3 空间天线桁架结构展开后轨道机动过程动力学分析

在空间天线桁架结构展开完成后长期工作的过程中,结构受力构件为完成展开的桁架.因此,为研究已展开结构的轨道机动问题,对在3.2节中描述的模型进行简化,保留模块中的对接结构,将展开桁架部分等效为柔性梁.其中,等效柔性梁的横截面积与抗弯刚度等于展开桁架中一层各承力杆横截面积与抗弯刚度之和,总质量和总长度等于模块中展开桁架部分的质量与长度.整个结构两侧各有5个简化后的模块.模型参数如表4所示.

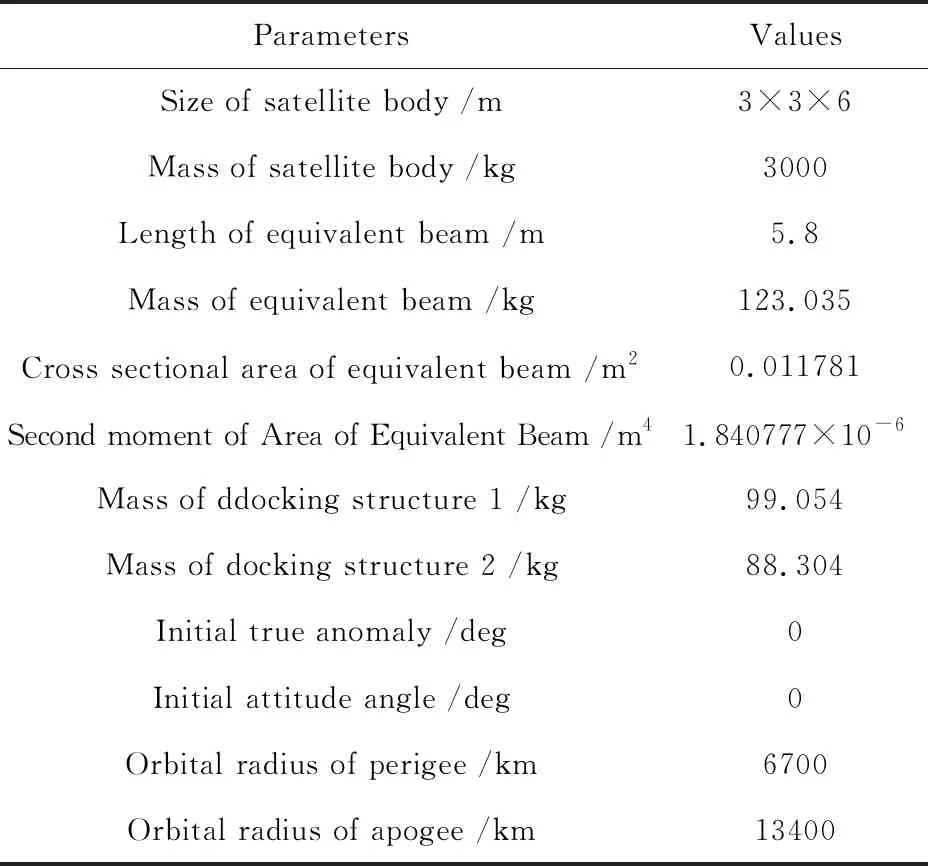
表4 空间天线桁架结构展开后轨道机动模型参数

结构轨道机动过程如图7所示.假设结构在轨道机动开始时刻获得一个速度变化量,使空间结构进入转移轨道的近地点;在运行到转移轨道远地点时获得另一个速度变化量,使空间结构离开转移轨道.在要研究的轨道机动过程中,结构位于只受地球引力作用的开普勒轨道上,该轨道为大偏心率椭圆轨道.

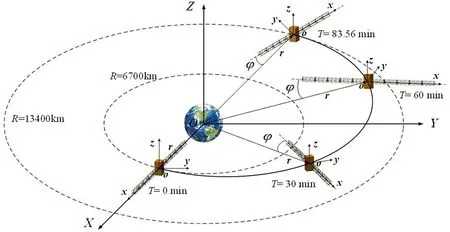
图7 空间天线桁架结构展开后轨道机动示意图Fig.7 Schematic diagram of orbital maneuver of deployed space antenna truss structure

在地心O建立三维惯性坐标系O-XYZ,OX轴指向椭圆轨道的近地点,OZ轴沿地球自转轴,OY轴方向通过右手定则确定.初始时刻模型质心o位于近地点,连体坐标系设置和3.2节中相同.将结构质心o在惯性系中的位置矢量r和连体系ox轴之间的夹角φ定义为结构姿态角;将末端对接结构质心相对于星本体质心的位置矢量在ox,oy方向上的投影为定义末端轴向位移和横向位移.

分别采用保能量动量时间积分算法和广义α算法计算结构的动力学响应.广义α算法的谱半径取为0.8.两种算法的时间步长取2×10-4min.图8给出了两种算法的动力学响应计算结果,包括结构姿态角、轴向位移与横向位移.其中,用“EM method”表示保能量动量时间积分算法,“GA method”表示广义α算法.

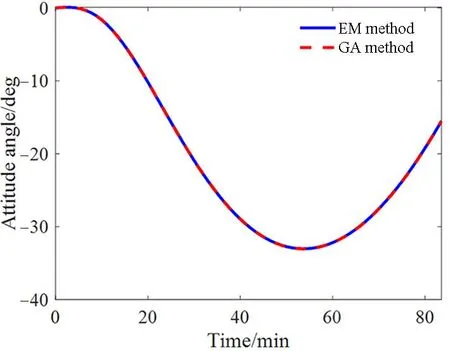
(a)结构姿态角曲线

由图8(a)可知,轨道机动过程中的结构产生了明显的姿态运动,结构姿态角即图7中的φ角最小值为-33.04°.对比图8(b)与图8(c)可以发现,结构的轴向变形大约1×10-5m量级,横向变形大约0.01m量级.因此,由椭圆轨道半径的变化产生的重力梯度导致结构产生大范围姿态运动,整体姿态角呈现先减小后增大的趋势.轨道机动过程中,结构的变形主要体现为横向变形.结构的柔性振动存在高频振荡,轴向振动与横向振动的频率远高于姿态运动的频率.保能量动量时间积分算法和广义α算法关于展开后空间结构轨道机动过程中的计算结果总体上接近.

4 结论

本文基于能够描述系统大变形和大转动的ANCF方法和ANCF-RN方法建立了模块化空间天线桁架结构刚柔耦合动力学模型,采用保能量动量时间积分算法和广义α算法计算结构在轨展开与轨道机动问题的动力学方程组,分析了重力梯度对结构动力学响应的影响.通过柔性空间结构动力学问题中经典算例的对比分析发现,保能量动量时间积分算法的计算结果比广义α算法的计算结果相对能量误差更小.重力梯度对展开过程中空间结构的姿态运动存在明显影响,随着结构整体刚度下降结构的横向变形呈现增大的趋势.展开后空间结构在轨道机动的过程中受到重力梯度的影响会产生明显的姿态运动和结构变形,结构变形主要体现为横向变形.