滚动轴承支承下松动-裂纹耦合故障转子系统动力学特性分析*

李姚 南国防 丘学文 姚夏

(上海理工大学 能源与动力工程学院, 上海 200093)

引言

在转子系统中,松动和裂纹是常见的故障.用于固定转子系统的螺栓由于制造和安装误差,在长时间的工作后易出现预应力不足、间隙过大等现象,进而导致转子支座松动故障.由于支座松动的影响,转子系统振动响应异常增大,进而易在轴系上产生裂纹.这种松动-裂纹耦合故障的转子系统在运行时,会呈现复杂的非线性动力学特性,对转子安全稳定运行造成不可预知的损伤.研究转子系统松动-裂纹耦合故障动力学特性,对机组故障诊断和健康监测均具有重要的学术价值和工程应用价值.

松动-裂纹耦合非线性动力特性的研究近年来成为转子动力学中的一个热点,路振勇等针对裂纹在转子系统下特有的时变性质,在对动力学方程进行谐波平衡法的近似求解过程中,发现位于跨中的深裂纹对系统的影响最为显著[1].Hong等提出了一种适用于转子松动系统的新型冲击减振器,发现该减振器能够有效抑制振动幅值[2].Wang等将三盘Jeffcott转子系统建模为单个单元.采用数值积分方法,将拟合松弛模型应用于转子的整体模型中,研究了转子的接触问题和响应特性[3,4].蒋勉等提出了基于动力学行为非线性度量的转子-滑动轴承系统支承松动状态评估方法[5],曲秀秀等通过数值仿真和实验研究发现盲源分离方法能够有效地实现耦合故障的分离[6].罗跃纲等研究了在裂纹-支承松动故障下的动力学响应,发现系统在同时出现了裂纹和松动故障时,松动对系统影响更大[7].伍小莉等研究了在不平衡-不对中-支座松动耦合故障系统下,考虑系统左端轴承支座松动的情况下松动间隙对系统动力学特性的影响[8].申倩等分析了转子系统下,裂纹扩展和裂纹角对系统的影响[9].钟志贤等对故障特征及其动力学特性的多故障转子-滚动轴承系统进行了探究[10].Huang等通过裂纹深度和裂纹角度对自行研究的模型进行了研究,并发现转子系统耦合故障下的不稳定形式极其复杂[11].谢沅博分析了偏心量和转盘速度对滑动支撑下的双盘转子系统动力学特性的影响[12].任双兴等建立了一种能应用于转子系统裂纹故障检测的区间控制策略模型[13].

Lin等在同向偏心距和反向偏心距两种工况下研究了滑动轴承支座松动时系统的动态特性[14].Wang等针对轴承外圈配合松动故障的转子对开闭裂纹的影响下双悬挂盘裂纹转子动力学系工况下研究了滑动轴承支座松动时系统的动态特-滚动轴承系统,建立了考虑轴承外圈与支座相互作用的转子耦合动力学模型,并通过仿真和试验验证了该故障的特点是周期性冲击、上下不对称、多频率,并提出了通过增大拧紧力矩来控制该故障引起的振动的方法[15].刘军等利用三维有限元法建立转子裂纹的模型发现了裂纹的出现会影响转子的工作频率,并提出了有效延缓裂纹扩展的方法[16].刘桂珍等发现当偏心量作为唯一控制参数时,即使微小的偏心量变化也可能导致系统的振动特性发生较大的变化[17].Guo等采用EMD方法检验裂纹,并结合快速傅立叶变换方法从实验振动信号的频谱中推导出高阶频率的幅值变化,证明了超谐波分量在1/3和1/2亚临界区域的变化是裂纹检测的稳定特征[18].

本文采用集中质量法建立转子系统非线性动力学模型,使用分段线性模型描述支座松动特性,转子横向裂纹采用综合模型来描述,研究松动质量、松动间隙和裂纹角对系统振动响应的影响.研究工作对于松动-裂纹转子系统的故障诊断有重要意义.

1 松动-裂纹耦合故障转子动力学建模

本文建立的松动-裂纹耦合故障动力学模型如图1所示.图中m1、m2分别为转子系统在轴承处和转盘处的质量,ms为松动端支座质量,c1、c2分别为转子在支承处和转盘处的结构阻尼,O1、O2分别为支承和圆盘的几何中心,O3为转盘的质心,轴承和转盘用忽略质量的弹性轴连接,且该系统不考虑陀螺力矩和扭转振动.建模中作出以下假设,(1)转盘视为刚体; (2)转轴质量远小于支承和转盘质量,将转轴简化为无质量刚性轴;(3)支座的A端发生松动,只需要考虑其在垂直方向上(y方向)的位移. 基于以上假设,建立转子系统动力学模型,以下将分别从滚动轴承、松动、裂纹等的动力学建模进行阐述.

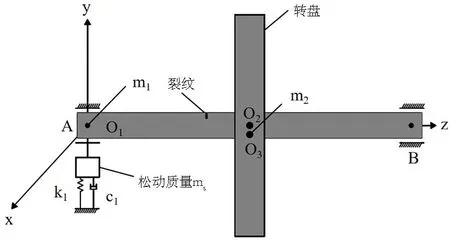
图1 松动-裂纹耦合故障转子系统示意图Fig.1 Schematic diagram of looseness-crack coupling fault rotor system

1.1 松动模型

转子支座松动会导致支承刚度发生变化,进而导致振动异常增大.为了研究支座松动对整机振动的影响机理,建立松动模型如图2所示,轴承座与底座连接有一处存在螺栓松动,松动间隙为δ1.转子松动端本文采用分段线性模型来表示轴承支座的刚度与阻尼,即支座垂直方向的振幅介于零与最大间隙之间时,刚度和阻尼等于零;若振幅超过最大间隙,由于受到支座上其他零部件的约束,此时刚度和阻尼不为零;若振幅为负,则刚度和阻尼亦不为零,刚度和阻尼的表达式如式1所示.

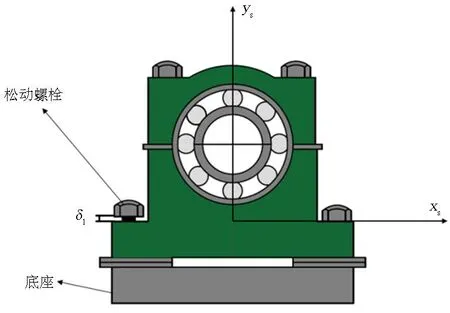
图2 松动模型示意图Fig.2 Loose model diagram

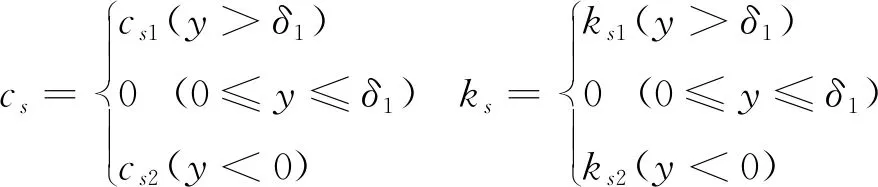
(1)

式中,δ1为表示轴承支座允许的最大间隙值,csi为不同y向位移下支座的等效阻尼,ksi为不同y向位移下支座的等效刚度,i=1,2.

1.2 滚动轴承

滚动轴承是将轴与轴承座相连的一种精密机械元件,其动力学建模关系到整个转子振动响应的计算精度.假设滚动体在滚道间均匀分布,运动状态为纯滚动,其表面速度与内外滚道接触点的速度一致,建立滚动轴承动力学模型如图3(a)所示,滚动轴承外环固定在轴承座上,内环与转子相连.为了研究单个滚珠的运动状态,对单个滚珠进行建模如图3(b)所示,滚动体与外环接触点的线速度为vo,与内环接触点的线速度为vi,假设轴承外环的旋转角速度为ωo,轴承内环的旋转角速度为ωi,外环半径为Ro,内环半径为Ri,则

(2)

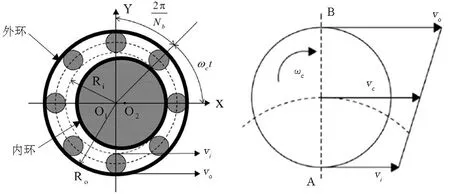
(a)整体剖视图 (b)局部图(a)The overall sectional view (b)topography

保持架即滚动体中心的线速度为:

(3)

由于内部轴承环与轴相连,内环的转动速度等于转子的转动速度,即ωi=ω,则:

(4)

设第j个滚珠处的接触角为j,且Nb为轴承的滚珠个数,根据滚珠j的角位置,可以得出滚珠在起始位置的角位移以及保持架在一段时间t内的转动角位移,这两者共同组成了滚珠的角位置.

(5)

滚动轴承的滚珠与内环、外环都是相互接触的,根据Hertz弹性接触理论,滚动轨道与滚动轴承的圆珠会产生非线性轴承变形荷载,该载荷可以表示为f=Cbu3/2,其中,Cb为Hertz接触刚度,u为发生接触后产生的变形量,滚珠j在发生弹性接触后产生的形变为uj,则:

uj=xcosβj+ysinβj-r,j=1,2,…,Nb

(6)

由非线性赫兹接触理论,只有uj>0时才有作用力,利用Heaviside函数H可知:

(7)

因此,fj在x和y方向上的轴承力分别为:

(8)

1.3 裂纹刚度模型

支座松动导致转子振幅过大,易在主轴产生横向裂纹.图4为裂纹示意图,ζo′γ为旋转坐标系,xoy为参考坐标系,Ω为轴心位移矢量方向角,β为不平衡量方向与裂纹法向夹角,O″为该横截面的形心.Δkζ和Δkγ分别为本系统裂纹轴在ζ和γ方向上的刚度变化量,则含裂纹转轴的刚度为:

图4 裂纹轴横截面示意图Fig.4 Cross section diagram of crack shaft

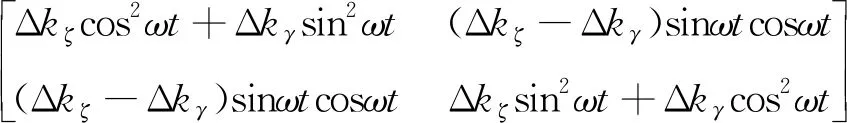
(9)

上述式中,ω为转子转速,Δkp(p=ζ,γ)为本系统裂纹轴在ζ、γ方向上的刚度变化量[19],k为转轴在无裂纹时的弯曲刚度,f(φ)为裂纹状态函数.本文使用的综合模型适用于各种复杂的含转轴横向裂纹的转子模型[20].

(10)

设系统左侧轴承处的水平位移和铅直位移分别为x1、y1,转盘处的水平位移和铅直位移分别为x2、y2,松动端支座垂直方向的位移ys,e为转盘的偏心量.基于滚动轴承、松动和裂纹动力学模型,依据拉格朗日第二类方程,建立系统运动微分方程如下:

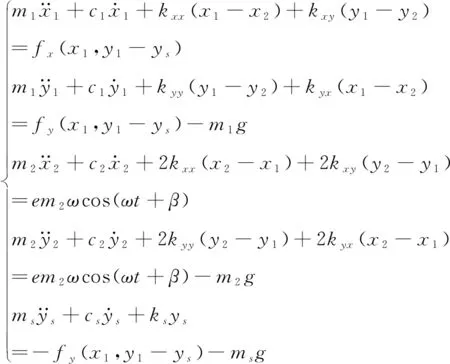
(11)

2 计算结果与分析

为研究转速、松动间隙、松动质量及裂纹角对转子非线性动力学特性的影响,采用四阶Runge-Kutta法对系统运动微分方程进行求解.算例采用的主要参数如表1所示.

表1 系统主要参数

2.1 转速对系统动力学响应的影响研究

为研究系统分别在仅裂纹故障和松动-裂纹耦合故障下的振动响应差异,本节分别对两种工况进行了动力学特性分析.

2.1.1 仅裂纹故障

图5为滚动轴承支承下仅裂纹故障时转子系统以转速为变参数的分岔图.由图可以看出,随转速ω的增加转子系统呈现出单周期、多周期、拟周期、混沌等多种非线性动力学特征.本节无量纲裂纹深度d/R=0.4,裂纹角β=π/2.

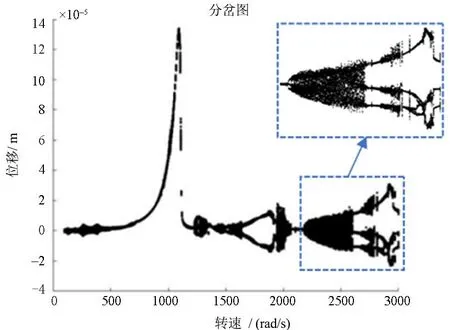
图5 裂纹转子系统振动位移响应随转速变化的分岔图Fig.5 Bifurcation diagram of displacement for cracked rotor system with the change of rotating speed

图6至图7分别为2300rad/s、2600rad/s时系统仅裂纹故障下的时域图、频谱图和Poincaré截面图.当ω=2300rad/s时,图6(b)频谱图中出现了1/3和2/3分频,Poincaré截面图中只有三个独立的相点,且图6(a)时域图显示了三种类型波峰,因此系统表现为周期3运动;当ω=2600rad/s时,由图7(a)时域图可以发现出现拍振现象,图7(b)频谱图中的1/3分频附近出现间谐波,图7(c)Poincaré截面图中出现一个分离的封闭圆环点阵, 系统将由周期3运动经过Hopf分岔进入拟周期运动.

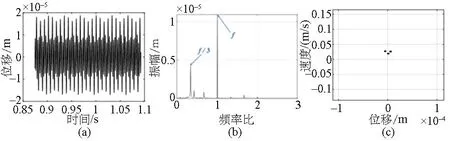
图6 ω=2300rad/s时系统振动信号分析图(a)时域图,(b)频谱图,(c)Poincaré截面图Fig.6 System vibration signal analysis diagram at ω=2300rad/s(a) Time domain diagram,(b) Spectrum diagram,(c) Poincaré section

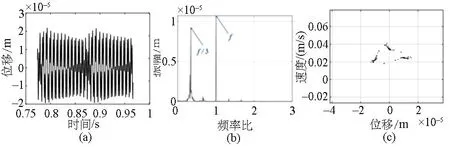
图7 ω=2600rad/s时系统振动信号分析图(a)时域图,(b)频谱图,(c)Poincaré截面图Fig.7 System vibration signal analysis diagram at ω=2600rad/s(a) Time domain diagram,(b) Spectrum diagram,(c) Poincaré section

2.1.2 松动-裂纹耦合故障

转子在支座松动下长期运行会出现裂纹故障,在松动和裂纹故障共存时系统非线性动力学特性更为复杂.图8为滚动轴承支承下松动-裂纹耦合故障时转子系统以转速为变参数的分岔图.本节无量纲裂纹深度d/R=0.4,裂纹角β=π/2,松动间隙δ1=1×10-5m.

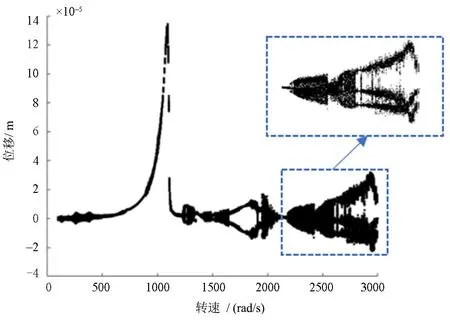
图8 裂纹转子系统振动位移响应随转速变化的分岔图Fig.8 Bifurcation diagram of displacement for cracked rotor system with the change of rotating speed

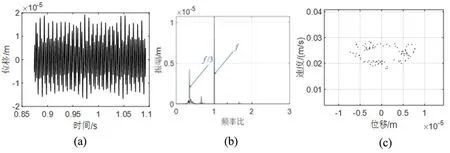
图9 ω=2300rad/s时系统振动信号分析图. (a)时域图 ,(b)频谱图,(c)Poincaré截面图Fig.9 System vibration signal analysis diagram at ω=2300rad/s. (a) Time domain diagram,(b) Spectrum diagram,(c) Poincaré section

图 9 至图 10 分别为ω=2300rad/s、2600rad/s时系统耦合故障下的动力学响应图.对比图5和图10可知,在系统增加了支座松动故障之后,系统低转速时系统分岔响应变化不大,当转速ω=2000rad/s之后,系统非线性响应明显增强.由图8可知,在ω=2300rad/s时,系统由原来的拟周期运动进入混沌运动.当ω=2600rad/s时,图 10(b)频谱图中存在1/3和2/3分频,且庞加莱截面图为三个分散的点,系统处于周期3运动中,在短暂的周期3运动之后,系统再次进入混沌运动.

图10 ω=2600rad/s时系统振动信号分析图. (a)时域图 ,(b)频谱图,(c)Poincaré截面图Fig.10 System vibration signal analysis diagram at ω=2600rad/s.(a) Time domain diagram,(b) Spectrum diagram,(c) Poincaré section

2.2 松动间隙对系统动力学响应的影响研究

松动间隙是表征支座松动的一项关键参数,深入研究松动间隙对系统动力学特性的影响十分必要.分别选取松动间隙为0.001mm、0.006mm和0.06mm.采用Runge-Kutta法求解式(13)中的振动方程,转速在100rad/s～3000rad/s间变动,计算得到转盘水平方向的振动位移幅值随转速变化的分岔图,如图11所示.

(a)δ1=0.001mm

根据以上分岔图,可以发现当系统达到高转速时即框图所示,不同松动间隙振动响应区别较大,因此为深入研究松动间隙变化对系统响应的影响,选取转速为2800rad/s时的各间隙对应振动响应进行对比,图12～图14分别为转速=2800rad/s时的轴心轨迹图、时域图以及频谱图.

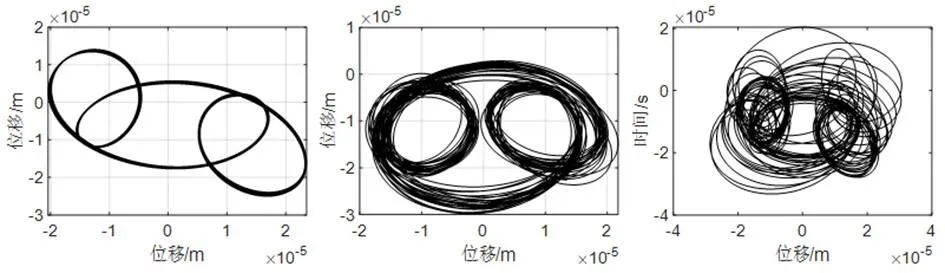
(a)δ1=0.001mm (b) δ2=0.006mm (c)δ3=0.01mm

对比图12和图13,在相同转速和裂纹深度下,随着松动间隙逐渐增加,转子振动位移逐渐增大,转子的横向位移偏离平衡位置愈发明显,轴心轨迹的椭圆由规则到混乱,这是因为周期出现了改变;随着松动间隙增大系统振幅逐渐增大,且由Poincaré截面图可以看出,当松动间隙变大,系统由原先的周期3运动逐步发展为混沌运动.

(a)δ1=0.001mm (b) δ2=0.006mm (c)δ3=0.01mm

2.3 松动端轴承支座质量对系统动力学响应的影响研究

松动端轴承座质量亦会对系统动力学特性产生重要影响.取裂纹深度d/R=0.4,裂纹角β=π/2,松动间隙δ1=6×10-6m,转速ω=2700rad/s,松动质量ms依次取25kg、45kg、65kg、85kg,研究松动质量对耦合故障的影响.计算得到各松动质量下频域图,如图15所示;随松动质量变化的振动响应分岔图如图14所示.

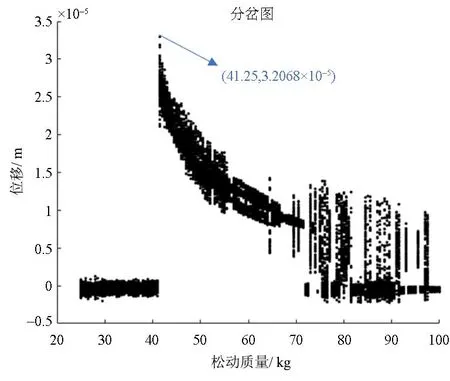
图14 耦合故障系统随松动质量改变振动响应分岔图Fig.14 The vibration response bifurcation diagram of the coupled fault system changes with the loose mass

(a)ms=25kg (b)ms=45kg

由图14可以看出,当松动质量较小时,即松动质量ms<41kg时,系统振动幅值基本维持在一个稳定区间;当ms> 41kg时,系统分岔图振动位移出现突增现象,且随着松动质量的不断增加,系统振动幅值呈现下降趋势.图15为不同松动质量下的振动频谱图,由图可知系统1倍频基本保持不变,而1/3倍频则持续增大,频谱图的1/3倍频率部分均出现了不同程度的“削波”现象,且松动质量越小,系统1/3倍频的附近的低倍频成分更多.

2.4 裂纹角对系统动力学响应的影响研究

转子长期运行易产生横向裂纹,表征横向裂纹的重要参数是裂纹角,为了研究裂纹角 对系统动力学响应的影响,裂纹角分别取β=π/4、β=π5/4 ,无量纲裂纹深度d/R=0.4,松动间隙δ1=0.001mm,松动质量ms=50kg.系统动力学响应随裂纹角变化的计算结果如图16所示.图16(a)为β=π/4时系统转速分岔图,可以看出在区域Ⅰ内系统先后经历了拟周期和P1周期运动;在区域Ⅱ内系统运动依次为拟周期运动、P2周期运动、拟周期运动、P1周期运动、混沌周期、P2周期运动和混沌运动;在区域Ⅲ内系统由P2周期运动经由混沌运动进入P1周期运动,此时分岔图出现“收缩”的趋势;在区域Ⅳ内系统出现混沌运动与P3周期运动交替出现的现象,最终趋于P3周期运动.图16(b)为β=5π/4时系统转速分岔图,同样发现在区域Ⅰ内系统先后经历了拟周期和P1周期运动;在区域Ⅱ内系统运动依次为拟周期运动、P2周期运动、拟周期运动、P3周期运动、P1周期运动、混沌周期、P2周期运动和混沌运动;在区域Ⅲ内系统由P2周期运动经由混沌运动进入P1周期运动,此时分岔图出现“收缩”的趋势;在区域Ⅳ内系统经历混沌运动,P2周期运动,混沌运动,P3周期运动.

(a)β=π/4

综上可知,裂纹角对系统振动响应的分岔特性有重要影响.当裂纹角由π/4增大到5π/4时,系统在区间Ⅰ,Ⅱ,Ⅳ振动最大位移的幅值几乎未变化,但方向与之前相反,而区间Ⅲ振动幅值范围突增65.7%.

3 结论

本文对滚动轴承支承下松动-裂纹耦合故障的动力学模型进行研究,主要结论如下:

(1)松动-裂纹耦合故障的转子系统相比仅有裂纹的系统,在高转速区间内动力学行为更加复杂,混沌区域更为宽泛.松动-裂纹转子在高转速下运行时,较大的偏心力导致轴承支座被抬起,松动端的振动幅值增大,叠加裂纹产生的非线性特性,使得系统呈现更为复杂的动力学行为.

(2)松动间隙和松动质量对转子系统动力学特性有重要影响.随着松动间隙的增大,系统发生混沌的转速区间逐渐变宽,转子轴心轨迹趋于杂乱无章;当松动质量增大至41.25kg时,响应幅值突增数倍,发生“跳跃”现象.该研究对松动故障诊断和支座质量设计提供参考.

(3)裂纹角对转子临界转速和分岔特性均有明显影响.不同的裂纹角产生不同的转涡差角,转涡差角影响裂纹轴的刚度,进而对临界转速及系统振幅产生影响.当裂纹角由π/4增大到5π/4时,系统振动最大位移反向,区间Ⅲ振动幅值范围明显变宽.

(4)本文主要对滚动轴承支承下松动-裂纹耦合故障系统展开了研究,由于实际工程中的转子系统较为复杂,涉及到的因素很多,本文的研究在故障位置和故障类型方面仍存在不足,下一步的研究工作中将重点关注.