含参非线性扰动系统的闭轨分叉分析*
郭碧垚 周艳,2† 张伟 刘宇
(1. 内蒙古师范大学 数学科学学院, 呼和浩特 010022)
(2. 内蒙古师范大学 应用数学中心, 呼和浩特 010022)
(3. 广西大学 土木工程建筑学院, 南宁 530000)
引言
在微分方程定性理论中,关于极限环的研究是一个既有趣又困难的部分. 研究极限环与解决微分方程积分曲线族的全局结构问题之间有密切的联系[1,2],为了确定一个确定的系统是否存在极限环,庞卡莱首先提出了后继函数法[3]、小参数法和环域定理等重要理论. 其中,后继函数法在研究一些非线性动力系统的极限环的存在性、稳定性以及重次等性质时具有重要的作用,这一理论也进一步推动了非线性系统分叉问题的深入研究[4],如闭轨分叉,庞卡莱分叉等[5,6]. 近些年来,闭轨分叉问题是动力系统的分叉现象研究的一个热点问题[7-9],它既是一种局部分叉,又是动态分叉[10].当前,已有研究者对各类不同的动力系统进行极限环及闭轨分叉分析,得到了相关的结论[11-14].
由于大多数系统是无法具体求解的,使用后继函数法研究其闭轨分叉问题并不容易[15-19]. 对于一个确定的非线性系统而言,如何确定后继函数的具体表达式是非常困难的,另一方面,即使已经获得系统后继函数的表达形式,而具体计算其零点的个数也是很难做到的. 但是后继函数法依然是分叉理论研究的不可或缺的重要方法.本文通过给出一个非线性动力系统,借助于后继函数法对其闭轨分叉问题进行了有效的理论分析.
1 非线性系统的平衡点分析
自治非线性系统为
(1)
其中P,Q是x-y平面上的连续函数,且满足解的存在唯一性条件.
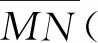
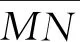
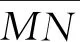
定义2无切线段上的点与其后继点(如果存在)的坐标之间的函数关系称为后继函数. 有时也把h(u)=g(u)-u称为后继函数.
由于后继函数在系统不动点附近的性态决定了非线性系统的轨线在极限环附近的性态. 由此,后继函数不仅可以用来研究极限环的存在性,还可以用来研究极限环的稳定性[20-25],为进一步揭示后继函数与极限环稳定性的关系,给出如下定理:
定理1如果后继函数h(u)满足
h(u0)=h′(u0)=…=h(k-1)(u0)=0,h(k)(u0)≠0,其中k∈Z+.则Γ0称为k重极限环.若k为奇数,h(k)(u0)<0(或>0),则Γ0是稳定(或不稳定)极限环; 若k为偶数,h(k)(u0)<0(或>0),则Γ0是外侧稳定而内侧不稳定(或外侧不稳定而内侧稳定)极限环.

任意u≠u0,且|u-u0|<ε,ε充分小,那么
h(u)=h(u0)+h′(u0)(u-u0)+…+

2 分叉周期解的方向和稳定性
在这节中,我们考虑如下系统:
(2)
其中,λ为扰动小参数.
系统(2)的未扰系统,即λ=0时的系统为
(3)
通过后继函数法可以判断出系统(3)有一个二重极限环Υ:x2+y2-1=0.
引入极坐标表示,系统(3)可以转化为
(4)
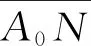
x=cosθ+ncosθ,y=sinθ+nsinθ.
(5)
在曲线坐标系中,坐标曲线θ=c是过点cosθ,sinθ)的法线,显然法线θ=0和θ=2π重合,坐标曲线n=c是闭曲线(也就是以原点为圆心的圆),由此可得以上闭轨Υ就是闭轨n=0,而对应的n>0的闭轨分布在Υ外侧,n<0的闭轨分布在Υ内侧.坐标变换式(5)的雅可比(Jacobian)式为
显然,对任何θ都有D=-n-1.因此, 存在足够小的δ>0, 使得当 |n|<δ时有D<0.这表明, 在闭曲线n=-δ和n=δ之间的环形邻域内. 若θ∈[0,2π),则两种坐标是一一对应的.
在环域|n|<δ内,将变换(5)式代入系统(3),我们有

(6)
易知
(7)
由式(6)和式(7),可得一个关于θ与n的微分方程
(8)
由于函数F(θ,n)在以上邻域内连续可微,故此邻域内的每一点,方程(8)都有唯一解.特别的有θ=0,n=0的解为闭轨Υ.
记方程(8)的满足初始条件θ=0,n=n0(|n0|充分小)的解为
n=Φ(θ,n0)
(9)

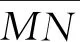
(10)
由于闭轨Υ对应于n=Φ(θ,0)≡0,因此,我们有g(0)=h(0)=0.
为了进一步确定闭轨的稳定性,下面考虑式(8)右端函数F(θ,n)满足
F(θ,0)=0
(11)
(12)
令θ=2π,得到系统的后继函数为
(13)
满足h′(0)=0,h″(0)=-16π<0.由定理1可知Υ是外侧稳定、内侧不稳定的二重极限环.
下面考虑原非线性系统(2)的闭轨分叉问题.当λ<0时,O(0,0)为系统(2)唯一的稳定平衡点;而当0<λ<1时,系统(2)有两个极限环: 它们的轨线方程为
x2+y2=1±λ
(14)
并且,当λ→0时,轨线(14)以λ=0时的二重环Υ为极限位置.
3 数值模拟
在这一节,我们将根据参数的不同取值来观察非线性系统的闭轨分叉发生的过程. 利用MATLAB软件绘图可得系统的动力学响应,对于不同取值的λ,分别给出了系统(2)在x2+y2=1邻近位置的相图.
通过上面的数值模拟结果,我们发现,当λ<0时,O(0,0)为系统(2)唯一的稳定平衡点,如图1所示;当λ=0时,系统(2)具有二重环Υ,系统的动力学响应如图2所示;当0<λ<1时,系统(2)有如图3所示的两个极限环.

图1 当λ=-1时,系统(2)的相图Fig.1 Phase portrait of system (2) when λ=-1

图2 当λ=0时,系统(2)的相图Fig.2 Phase portrait of system (2) when λ=0

图3 当λ=0.49时,系统(2)的相图Fig.3 Phase portrait of system (2) when λ=0.49
4 总结
本文分析了一类非线性系统的闭轨分叉问题,通过选择合适的坐标变换,获得系统的后继函数显式表达式,讨论了系统存在的极限环及其稳定性. 最后,通过MATLAB进行数值模拟,得到系统的动力学响应特性.

