滤子与滤子图
史艳维,姚 杰
(西安培华学院通识教育中心,陕西 西安 710125)
滤子与滤子图
史艳维,姚杰
(西安培华学院通识教育中心,陕西 西安 710125)
[摘要]讨论了有限集合上滤子与滤子图的性质.证明了有限集合上的滤子都是主滤子,并得到其基数的计算公式;通过给出滤子的后继定义了滤子图,讨论了滤子图的性质,进而绘制出了滤子图.
[关键词]滤子;主滤子;后继;滤子图
1937年法国布尔巴津学派的创始人之一Carten在研究拓扑空间中的Moore-Smith收敛理论时,提出了滤子的概念.作为网的概念的替代,滤子揭示了收敛理论中更加丰富的特征和属性.一般说来,滤子是偏序集合的一类特殊子集,通常考虑的是某个集合的幂集在集合包含关系下所得偏序集合的一类特殊子集,滤子不仅在拓扑学理论中得到充分发展,而且在模型理论、非标准分析理论、格论等数学其他分支中也得到了广泛的应用.[1-10]
本文主要讨论了有限集合上滤子和滤子图的性质,这为滤子理论与图论的结合发展提供了一种尝试.首先,证明了有限集合上的滤子都是主滤子,并且得到其基数的计算公式;其次,通过给出滤子的后继定义了滤子图;最后,讨论了滤子图的性质,进而绘制出了滤子图.
1有限集合上的滤子
定义1设x是非空集合,2x是x的幂集(即x的全体子集之族).F⊆2x,若F满足以下条件:
(1)x∈F,∅∉F;
(2)若A,b∈F,则A∩b∈F;
(3)若A∈F,且A⊆b∈2x,则b∈F.
那么称F是x上的一个滤子,并记x上的全体滤子族为F(x).
例1对于任意的A∈2x,A≠∅,令F(A)={b∈2x|A⊆b},则F(A)是x上的一个滤子,这是因为:
(ⅰ)由于A∈2x,且A≠∅,则显然x∈F(A),∅∉F(A);
(ⅱ)若b,C∈F(A),则A⊆b,A⊆C,于是A⊆b∩C,从而b∩C∈F(A);
(ⅲ)若b∈F(A),且b⊆C,则A⊆b⊆C,于是C∈F(A).
称此滤子为由A生成的主滤子,集合A称为主滤子F(A)的生成集.
例2设x是无限集.令Fx={A∈2x|x-A是有限集},容易验证Fx是x上的一个滤子.显然Fx不是x上的主滤子.
引理1设A,b∈2x.则A⊆b,当且仅当F(A)⊇F(b).进而,A=b,当且仅当F(A)=F(b).
证明对于任意的f∈F(b),f⊇b⊇A,于是f∈F(A).反之,因为b∈F(b),而F(b)⊆F(A),所以b∈F(A),从而A⊆b.
可见,主滤子完全由生成集所决定.由例2可知,在无限集上存在非主滤子,但在有限集合上,这是不可能的.
定理1设x是有限集.则F∈F(x),当且仅当存在A∈2x且A≠∅,使得F=F(A).
证明充分性由例1可得,下证必要性.若F是x上的一个滤子,由于x是有限集,则F是2x的有限子集,于是∩F=∩{f∈2x|f∈F}∈F,从而∩F≠∅,且对于任意的f∈F,∩F⊆f,即F=F(∩F).
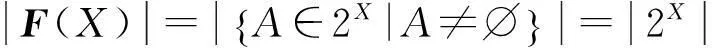
2滤子图
定义2设F(A),F(b)∈F(x),且满足以下条件:
(2)对于任意的F(C)∈F(x),F(A)F(C)F(b)不成立.
则称F(b)是F(A)的后继.
证明由定义2和引理1可得F(b)是F(A)的后继,当且仅当F(A)F(b)且对于任意的F(C)∈F(x),F(A)F(C)F(b)不成立,当且仅当Ab且对于任意的C∈2x,ACb不成立,当且仅当Ab且.
考虑有限集x上的滤子图g=(v,f),其中v=F(x),映射f:v→2v为后继映射,即对于任意的F(b)∈f(F(A))当且仅当F(b)是F(A)的后继.
关于滤子图,可以得到如下结论.
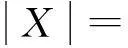
(1)g分为n层;


(4)第i(i=1,2,…,n-1)层中每个顶点的出度为n-i+1,第i(i=2,…,n)层中每个顶点入度为i-1.
证明(1)由定理2可知F(b)是F(A)的后继,当且仅当Ab且=1,于是两个滤子具有相同基数的生成集当且仅当它们在同一层,而=n,从而g分为n层;
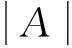


推论2在滤子图g=(v,f)中,F(A)∈F(x)是起点,当且仅当A=x;F(A)是终点,当且仅当A={x}(x∈x).换句话说,F∈F(x)是起点,当且仅当F是x上的最小滤子;F是终点,当且仅当F是x上的主超滤子.
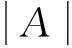
结合定理3中滤子图的性质,可以画出n=2,3,4,5,6时的滤子图,见图1—2.

图1 n=2,3,4时的滤子图

图2 n=5,6时的滤子图
[参考文献]
[1]BOURBAKI N.General topology[M].Paris:Addison-Wesley,1951:121-153.
[2]江辉有.拓扑学[M].北京:机械工业出版社,2013:102-117.
[3]马克.模型论引论[M].北京:科学出版社,2007:33-48.
[4]MARTIN DAVIS.Applied nonstandard analysis[M].New York:Oversea Publishing House,2005:6-21.
[5]史艳维,马春晖.Loeb空间的测度同构[J].东北师大学报(自然科学版),2013,45(4):28-30.
[6]陈东立,史艳维,董欢欢.向量函数微分的非标准定义[J].东北师大学报(自然科学版),2015,47(3):37-39.
[7]马春晖,李生刚,史艳维.由X上理想族诱导出的*X上的I-拓扑[J].东北师大学报(自然科学版),2010,42(3):14-17.
[8]史艳维,马春晖.由有限核生成的Loeb测度[J].华中师范大学学报(自然科学版),2013,47(6):759-762.
[9]史艳维,马春晖.符号Loeb测度以及符号测度的绝对连续性[J].浙江大学学报(理学版),2015,42(3)253-255.
[10]李海洋.一般格论基础[M].西安:西北工业大学出版社,2012:34-41.
(责任编辑:李亚军)
Filters and graph of filters
SHI Yan-wei,YAO Jie
(Center of General Courses,Xi’an Peihua University,Xi’an 710125,China)
Abstract:The properties of filters and graph of filters,on a finite set,are shown.Firstly,it is proved that all filters,on finite set,are principle,and the formula of its cardinal is obtained.Then,graph of filters is defined by follower of filter.At last,some properties of graph of filters are discussed,and some graph of filters are drawn.
Keywords:filter;principle filter;follower;graph of filters
[文章编号]1000-1832(2016)02-0011-03
[收稿日期]2015-04-02
[基金项目]陕西省自然科学基金资助项目(2007A12);陕西省教育厅科学研究项目(15JK2093);西安培华学院校级科研课题(PHKT20150734).
[作者简介]史艳维(1980—),女,硕士,讲师,主要从事非标准分析理论研究.
[中图分类号]O 144[学科代码]110·41
[文献标志码]A
[DOI]10.16163/j.cnki.22-1123/n.2016.02.003

