甘岑后继式演算系统与其自然演绎系统的比较

董文媛



甘岑后继式演算系统与其自然演绎系统的比较

董文媛

（山西农业大学信息学院创意写作中心，山西 太谷030800）

《逻辑演绎研究》“（Untersuchungen über das Logische Schliessen”）是甘岑提交哥廷根大学的就职论文，文中甘岑提出了两种逻辑演算系统，即“自然演绎”和“后继式演算”系统。从自然演绎开始甘岑尝试构造一个接近数学实际推理的逻辑演算，而后针对自然演绎系统的不足进行了转化和改进，构造了后继式演算系统，并证明了该逻辑演算系统的合理性。甘岑的逻辑演绎思想在逻辑史上具有十分重要的地位，对现代逻辑和证明论的发展具有深远的影响。

自然演绎；后继式演算；逻辑演算系统

1　甘岑后继式演算系统

1.1从“自然演绎”到“后继式演算”

继希尔伯特和阿克曼的《数理逻辑基础》之后，甘岑（Gerhard Gentzen 1909-1945）于1934-1935年分两部分发表的论文《逻辑演绎研究》（“Untersuchungen über das Logische Schliessen”英译为“Investigations into logical deduction”）中提出了“自然演绎”（Natural deduction）的概念。哥德尔在不完全定理证明之后，进一步提出了数论一致性的不可证问题，甘岑则以构造数论的一致性证明为目标，将逻辑演绎的形式化作为出发点进行尝试。他认为弗雷格、罗素和希尔伯特的形式系统远离了数学证明中实际使用的演绎形式，因此为了使形式证明尽可能地接近自然的、实际的推理，使结论独立于假设成为“纯逻辑”的证明，并且达到可观的形式上的优越性，构造了自然演绎系统。［1］288自然演绎是一种证明演算，在这种逻辑演算中，不同于公理系统演算包含公理和推理规则，自然演绎系统是只包含推理规则，更加接近自然的实际推理。

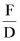
1.2后继式演算

基于自然演绎系统存在的不足，甘岑尝试建立一个新的逻辑演算系统，在自然演绎系统的基础上进行完善，分别构建完善了古典谓词逻辑和直觉主义谓词逻辑的演算系统，为“切割消除定理”和数论一致性提供了完整的证明。一方面这个系统要继承自然演绎推理规则中“引入”和“消去”的逻辑符号规则系统，另一方面要改变自然演绎的形式，这个系统是“逻辑的”，即其中的推导不含有假设公式。这个新的系统甘岑称之为后继式演算（Sequent Calculus）系统，同样甘岑分别构建了直觉主义谓词逻辑后继式演算系统（简称为“LJ”）和古典谓词逻辑后继式演算系统（简称为“LK”）。

在自然演绎NJ系统基础上，甘岑做了一些改动来构建LJ系统。首先用新公式（A1&...&Aμ）ÉB来替换依赖于假设A1，...，Aμ的D-公式（推导公式）B。［1］295将所有这种情况下的D-公式这样替换，我们就得到了（A1&...&Aμ）ÉB这种自身有效的公式，它们的真不再以一些假设公式的真为条件。但是这样在推理图的下层公式中就引入了新的逻辑符号&和É，所有的推理图在原有基础上都必须增加&和É的推理图，这便扰乱了引入和消去逻辑符号系统的特征。因此，甘岑引入了后继式的概念。

一个后继式是具有如下形式的表达式［1］290：

A1，...，Aμ—→B1，...，Bv

其中A1，...，Aμ和B1，...，Bv可以代表任何公式，符号“—→”像逗号，是辅助符号，不是逻辑符号。公式A1，...，Aμ形成该后继式的前件（Antecedent），公式B1，...，Bv则形成该后继式的后件（Succedent）。这两种表达式都可以为空。

后继式与下面这个公式在直观上有相同的意义：

（A1&...&Aμ）É（B1∨...∨Bv）

如果前件为空，那么这个后继式就归约为公式B1∨...∨Bv；

如果后件为空，那么这个后继式与公式Ø（A1&...&Aμ）或（A1&...&Aμ）ÉF的意思相同；

如果前后件两个部分都为空，那么这个后继式意思与F相同，即为假命题。

反之，每个公式都有一个相应的等价后继式，例如前件为空而后件恰由那个公式构成的后继式（公式A等价于后继式—→A）。

组成一个后继式的公式称为S-公式（即后继式公式）。这样规定我们是想表明，我们不是在考虑公式本身，而是考虑它在后继式中的出现（与D-公式类似）。比如我们说：“一个公式作为一个S-公式在一个后继式中几处出现”，这也可以表达如下：“几个不同的S-公式（这仅仅意谓：该公式在该后继式中有不同的出现）在形式上是相等的”。［1］290也就是说一个公式，在后继式中不同的位置出现，虽然形式相同，但是我们把它的每次出现都看作一个不同的S-公式。关于推理图和推导的定义，后继式演算沿用了自然演绎推理图和推导的定义，只不过在后继式演算的推理图由上层后继式和下层后继式构成，后继式演算的证明仍然是树形的。那么由一个后继式构成的推导中，一个推导中出现的后继式称为D-后继式（即推导后继式），D-后继式的S-公式称为D-S-公式（即推导后继式公式）。［1］291

构建LJ系统时我们不使用公式（A1&...&Aμ）ÉB这种形式，而写成后继式的形式：A1，...，Aμ—→B，根据后继式的定义得知，这个公式与它的后继式形式在直观意义上没有区别，只是在形式结构上有所差别。［1］291

甘岑进一步构造了一些新的推理图，这些推理图不能整合到引入和消去推理图系统中，它们不需要参照逻辑符号，而是参照后继式的结构，将这些推理图在系统中保留特殊的位置。甘岑将这些新加入的关于后继式结构的推理图称为“结构推理图”，而其余的参照逻辑符号的推理图称为“算子推理图”。以上甘岑构造谓词逻辑后继式演算系统的主要方法。

此外，甘岑还解决了在古典谓词逻辑自然演绎系统中，排中律无法整合入引入和消去的系统中的问题。在后继式演算系统中，甘岑则运用限制后继式形式结构上的差别来区别LJ系统和LK系统，即LJ-系统中只允许后件是不能超过一个S-公式的后继式，而在LK系统中允许后件带有多个S-公式的后继式进入。表面看来，结构上的限制没有体现排中律的特殊地位，但实际上，甘岑巧妙的运用这样的方法，在直觉主义谓词逻辑后继式演算系统中排除了排中律，即排中律“A∨ØA”，其后继式“—→A∨ØA”在LK系统中可证，在LJ系统中不可证。如此看来，根据后继式的定义，这样得到的古典谓词逻辑后继式演算系统更符合后继式的对称性，在形式上更加优雅。

甘岑构造的后继式演算系统，在形式上很大程度是由要证明他所提出的“法则”即“切割消除定理”相关的考虑决定的，而子公式性质（Subformula property）则是这一“法则”的推论。因此，在后继式演算系统中我们可以完整的证明这个形式系统的合理性，弥补了自然演绎系统的不足。

2　后继式演算系统与自然演绎系统的比较

2.1系 统构造比较

首先，后继式演算系统的构造是在自然演绎基础上的一个拓展。自然演绎推理图中的基本单位为公式，在一个推导中，结论是由一个公式构成，在后继式演算系统中，甘岑将推导的结论扩展为一个公式后继式，引进了后继式的概念A1，...，Aμ—→B1，...，Bv。为了避免推理图产生混乱，甘岑用“—→”这个符号，将公式用逗号隔开来表示公式（A1&...&Aμ）É（B1∨...∨Bv）。这样在后继式演算中，推理图是由上层后继式和下层后继式构成。其次，后继式演算的推导是以基础后继式D—→D为初始后继式的，而自然演绎是以假设公式作为初始公式。对推理图进行这些规范化之后，后继式演算解决了“不可证”的问题，即对一个后继式进行证明，如果最终初始后继式不是基础后继式的形式，则这个后继式不可证，在自然演绎中这个问题并没有得到解决。此外，经过这样的构造使得证明具有更加优美、完善的形式。特别是表现在古典逻辑中，由于LK演算推理图中的后继式后件可以包含多个S-公式。所以LK演算的推理图具有对称性，证明形式更加优雅。

其次，后继式演算系统的推理图模式与自然演绎系统明显不同。后继式演算系统的推理图，包括两个部分，“算子推理图”和“结构推理图”。甘岑不仅新添加了结构推理图，并且算子推理图的形式也与自然演绎系统的推理图有很大差别。甘岑这样构造推理图，是出于提供一个标准化定理的证明为目的，即“切割消除定理”的证明。另一方面，这样使得后继式演算的形式更加简洁、优雅。算子推理图尽管在形式上看起来与自然演绎系统的算子推理图有很大差异，一是分了前件和后件规则，二是只有引入规则。但实际上与自然演绎系统推理图的引入和消去系统的构造方法一致，每个算子的后件引入规则对应了自然演绎中的引入规则，其前件引入规则则对应了自然演绎中的消去规则。

最后，LJ与LK演算的区别，和NJ与NK演算的差别看起来完全不同。NJ与NK演算的区别于是否包含排中律，而LJ与LK演算的区别则是规定了在LJ演算中，只允许推理图中的后继式后件至多包含一个S-公式，在LK中可包含多个S-公式。实际上LJ与LK演算的区别虽然表现在形式上，实际反映的区别与NJ与NK演算相同。通过对LJ进行限制，排中律A∨ØA排除在了LJ系统之外，在LK中，排中律A∨ØA则可以得到证明。在LK中甘岑给出了“—→A∨ØA”的证明［1］297：

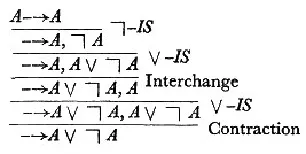
但在LJ中，后继式后件至多包含一个S-公式，因此我们只能进行到以下步骤：

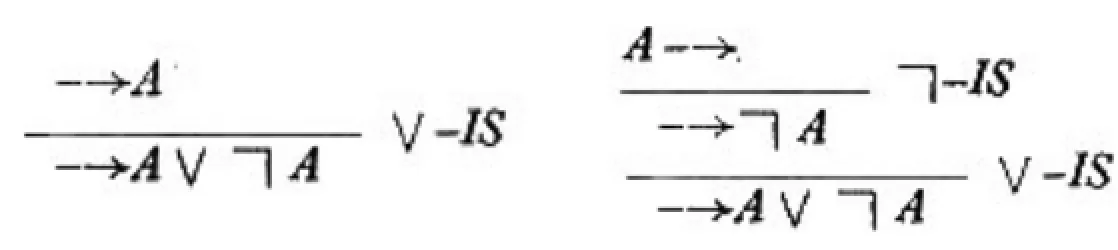
初始后继式不是基础后继式的形式，因此，在LJ系统中“—→A∨ØA”不可证。

2.2系 统中证明过程比较

从形式上来看，后继式演算系统与自然演绎系统的证明都是树形的，非循环的。但是二者在形式上存在很大的差别。以（Ø$xFx）É（"yFy）的证明为例：

在LJ系统中的证明［1］297：

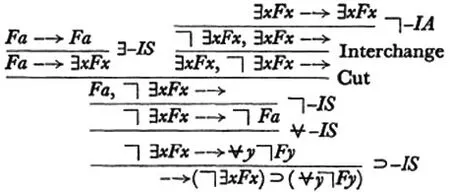
在NJ系统中的证明［1］294：

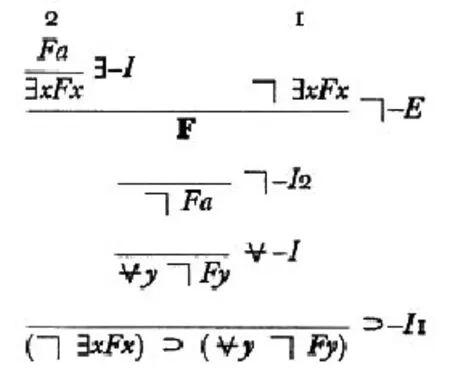
第一，在后继式演算中，证明中的推理图是由后继式构成的；而自然演绎中的推理图是由公式构成的。第二，后继式演算证明是以D—→D的基础后继式开始，称为初始后继式，在整个证明中没有假设；自然演绎证明则是由假设公式作为初始公式，对初始公式没有规定标准的形式，因而自然演绎的证明形式与后继式演算相比不够标准。第三，后继式演算中引入结构推理图，使得证明更加标准，其中特殊的切割规则，会使一个公式“消失”，在这个例子中消去的是$xFx，仍然保持了子公式性质，但是，由于推理图中公式D是任意的，切割规则消去的可能是结论后继式中S-公式的子公式之外的公式，也就是说可能会破坏子公式性质；自然演绎系统中没有结构推理图，仍然保持子公式性质。在后继式演算中，切割规则虽然会破坏子公式性质，但是甘岑证明了“切割消除定理”，即每一个后继式演算中的推导，都可以转化为有同一个尾后继式的没有切割规则出现的推导。而子公式性质作为一个推论也得以证明，即在一个没有切割规则出现的后继式演算推导中，出现的所有D-S-公式都是出现在尾后继式（Endsequent）中的S-公式的子公式。

根据子公式性质，加之后继式演算的标准证明形式，我们可以在后继式演算推导中进行“证明搜索”。即当我们给出一个后继式需要在后继式演算中证明的时候，这个后继式作为树形的“根”出发向上进行搜索，如果这个推导可以一直进行搜索直至它的每一个支都以“D—→D”的基础后继式结束，那么这个后继式在后继式演算系统中就是可证的。反之，如果我们进行搜索时以非D—→D形式的后继式结束，那么这个后继式在后继式演算系统中就是不可证的。例如我们之前的排中律的证明，在LK系统中对后继式“—→A∨ØA”进行搜索，最终以“A—→A”结束，因此该后继式在LK系统中可证，也就是排中律包含在LK系统之中。

在LJ系统中，我们进行了所有可能的尝试，对后继式“—→A∨ØA”进行搜索，但是两个推导分别以“—→A”和“A—→”结束，因此该后继式在LJ系统中不可证，也就是说LJ系统将排中律排除在外。

证明搜索是后继式演算系统特有的，我们可以提供可证和不可证的证明。自然演绎系统中我们可以证明一个系统内的定理，但是如果一个定理在自然演绎系统中不可证，那么它的推导会陷入循环，无法停止，因此自然演绎系统无法给出一个系统外定理的不可证的证明。

此外，如果在LK演算中去掉É-IS（É的后件引入规则）和É-IA（É的前件引入规则），LK演算则具有对偶的特殊性质。假设一个不包含É-IS和É-IA的LK推导，我们将其所有的后继式做如下的转换：将A1，...，Aμ—→B1，...，Bv转换为Bv，...，B1—→Aμ，...，A1；将有两个上层后继式的推理图，将两个上层后继式包括它们各自的推导进行左右转换；并将所有的&替换为∨，"替换为$，∨替换为&，$替换为"（在&与∨的互相替换中，要将其命题变元也进行转换，如A&B用B∨A替换）。这样替换之后我们会发现这个对偶性质，以&-IS为例：

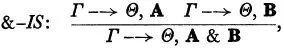
进行转换后：

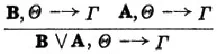
这时我们会发现，进行左右的转换之后，&-IS转变为∨-IA。以此类推，其余的推理图也可以进行这种转换，因此只有LK演算具有这样的对偶性质，进而充分说明LK演算的证明具有对称性。

综上，甘岑的后继式演算系统是对自然演绎系统的扩展，基于提供“切割消除定理”的证明这一目的，甘岑构造出了形式上更加标准，更加完善的逻辑演算。相比自然演绎系统，第一，后继式演算系统将结论由一个公式拓展为多重结论，即后继式；第二，在推导中规定了基础后继式“D—→D”为初始后继式；第三，构造了“结构推理图”和“算子推理图”两种推理图，并且将自然演绎系统的引入和消去模式，以前件和后件的形式进行的继承和完善；第四，为“切割消除定理”提供了一个完整的证明，得出了子公式性质这个推论。第五，基于以上，后继式演算产生了“证明搜索”的性质，可以提供一个后继式可证和不可证的证明。至此，甘岑成功地构造了后继式演算系统，弥补了自然演绎系统的不足，证明了这个逻辑演算系统的合理性。

3　总结与展望

逻辑学与数学的结合，即用数学的研究方式研究逻辑推理，是现代逻辑发展的标志。弗雷格借鉴了数学的形式系统构造方法，创造了一套属于逻辑学的形式语言，即“概念文字”，并且分别构建了命题逻辑和谓词逻辑的形式化的公理系统。逻辑学以“概念文字”为开端，运用数学的研究方法来研究推理，数理逻辑应运而生，初步实现了传统逻辑到现代逻辑的转变。希尔伯特与他的学生阿克曼在弗雷格“概念文字”的基础上，继怀特海和罗素的《数学原理》之后，在《数理逻辑基础》一书中对弗雷格的命题逻辑和谓词逻辑的形式系统进行了完善，构造了“希尔伯特式的公理系统”。基于这样一套完整的形式系统，构建的形式证明更加优美，对证明论的发展也具有里程碑的历史意义，因此希尔伯特被誉为数理逻辑和证明论的奠基人之一。

弗雷格、罗素和希尔伯特构建的形式系统，借鉴了数学的公理系统，以公理和规则为基础，其形式证明在甘岑看来，实际上远离了数学证明中使用的演绎形式。因此继希尔伯特和阿克曼之后，甘岑在《逻辑演绎研究》中提出了“自然演绎”的概念。自然演绎是一种证明演算，在这种逻辑演算中，没有公理，只包含推理规则，其推导从假设开始，更加接近自然的实际推理。甘岑的“自然演绎”则是继弗雷格之后的又一次“惊艳”的创造。它突破了公理系统的模式，给我们提供了一种更接近实际推理的证明系统。“自然演绎”系统的构造，不仅是现代逻辑史上，同时也是证明论史上的又一个里程碑。

在自然演绎系统的基础上，甘岑针对其不足进行了进一步的完善，构造了后继式演算系统。其优势主要体现在两个方面，一方面是经过对自然演绎的扩展，基于这个完整的形式系统，甘岑为“切割消除定理”构造了完整的证明，得出了“子公式性质”。另一方面，基于子公式性质，和对形式证明的规范，后继式演算具有的“证明搜索”的特性。在后继式演算中可以对任意公式的后继式根据推理规则向上进行搜索，并且搜索可以停止。如果搜索以基础后继式“D—→D”作为结束，那么这个后继式在系统内是可证的，如果以基础后继式以外的后继式结束，则不是系统内可证的，解决了自然演绎的不可证问题。至此，甘岑完整的构造了他的逻辑演算系统，并证明了该系统的合理性，在现代逻辑史上和证明论史上迈出了划时代的一步。

甘岑的《逻辑演绎研究》对数理逻辑和证明论的发展具有深远的影响，继甘岑之后，众多国外的学者发展了它的逻辑演绎思想。“科多能（Oiva Ketonen芬兰）和克里（Haskell B.Curry美国）扩展了对后继式演算的处理，舒特（Kurt Schütte）将甘岑的切割消除定理转移到通常的逻辑演算。洛伦兹（Paul Lorenzen）和舒特运用“无穷归纳”研究了切割消除定理在证明论中的应用。后来竹内外史（Gaisi Takeuti日本）将甘岑演算推广到一个能够使实数理论形式化的类型论系统。虽然竹内外史没有证明切割消除定理，但是他证明假定广义切割消除定理可以得出他的系统的一致性。”［1］288因此，甘岑的逻辑演绎思想在现代逻辑史上和证明论史上占有十分重要的地位，为现代逻辑和证明论的发展提供了方向，具有里程碑式的历史价值。

［1］Gentzen G.Investigations into logical deduction［J］.American Philosophical Quarterly，1964（1）:4.

Comparative Analysis to Gentzen’s Subsequent Calculus System and Natural Deduction System

DONG Wen-yuan
（College of Information，Shanxi Agricultural University，Taigu，Shanxi030800，China）

Gerhard Gentzen’s inaugural dissertation for the University of Göttingen，Investigations into Logical Deduction（Untersuchungen über das Logische Schliessen），in which he developed two forms of logic deduction，the natural deduction and subsequent calculus.Gentzen introduced his work by starting first from a natural deduction，which is closing to the the actual reasoning in mathematical proofs，and by then transforming it to a subsequent calculus，in which Gentzen gave a proof of the consistency of this system. Gentzen present his thought of logic deduction in this paper，and made a deeper work on the logic calculus. Gentzen’s thought of logic deduction is the milestone in the history of logic，and the study on his theory still has has great theoretical value and significance.This paper briefly describes the structure of Gentzen’s subsequent calculus’system，furthermore，the author makes a comparative analysis to subsequent calculus and natural deduction.

Natural Deduction；Subsequent Calculus；Logic Calculus System

B81

A

2096-0239（2016）03-0066-06

（责编：彭麟淋责校：明茂修）

2016-05-11

中央高校基本科研业务费专项资金一般项目“达米特直觉主义逻辑演绎研究”，项目编号：SWU1609140。

董文媛（1989-），女，山西太原人，山西农业大学信息学院创意写作中心教师，硕士。研究方向：哲学逻辑与逻辑哲学。