民机电驱动刹车系统动力学研究综述*

赵兰浩 黄健哲

(1. 上海飞机设计研究院 机电事业部,上海 201210)

(2. 上海交通大学 航空航天学院,上海 200240)

引言

近年来,全球航空业得到了突飞猛进的发展,航运量每年都以至少百分之四的速度增长,由此产生了大量的温室气体,与全球大力发展绿色产业以改善人类生存环境的大背景相矛盾.另外,航空飞行器温室气体的排放超过四分之三来自大型飞机[1],促使商业飞机生产商不得不考虑采用绿色能源代替传统能源,以实现碳达峰、碳中和目标.早在第二次世界大战时期,美国军机制造商提出了飞机电气化的概念,为了提高飞机的可靠性、降低维护成本.但是当时的电力和电子技术发展相对滞后,美军基地的工程师针对液压动力和电子动力进行了比较研究后,仍然认为液压动力是当时的最优方案.因此,军机和民机依然采用机械、液压、电等混合能源来为飞机提供动力.1956年,美国贝尔实验室发明了p-n-p-n触发晶体管[2],随后德国GE公司推进了三极管的商业应用.自此,电力电子技术得到了突飞猛进的发展,其中包括电机的PWM控制技术和固态、高功率密度的电子元件.20世纪90年代早期,MOS控制晶体管(Metal Oxide Semiconductor-Controlled Thyristor, MCT)被研发出来,并获得当年度美国研发杂志颁发的“R&D 100”奖励,它的发明使得多电/全电飞机的概念变得可行.

根据Lockheed的研究,如果将300架拥有500个座位的全电飞机投入到国际航线中,运营16年最高将带来90.4亿美元的净利润(根据燃油价格1.8美元/加仑、每年每架飞机7.5亿美元每座位里程营收估算)[3].当时的飞机已经有92%的组成部分实现了电气化,只需要将飞控、刹车的驱动器由液压代替为机电装置,并采用电推进代替气动推进,就可以实现飞机的全电化.因此,当时美国对全电飞机的项目表现非常乐观.虽然,多电飞机是全电飞机的过渡态,但其概念已经十分接近于全电飞机,仅有推进模块不是全电模式.20世纪90年代晚期,美国Joint Strike Fighter (JSF)计划在研发下一代战机的时候就引入了多电飞机的概念,并计划在C-141运输机、F-18和F-16战斗机上采用电驱动的飞行控制作动面.同时,欧洲的Future Offensive Aircraft (FOA)也开始研究多电飞机的技术和方法[4].在民用方面,空客和波音都将注意力投向了多电概念,并将其投入到新型大飞机的研发中.

不管是多电飞机还是全电飞机,均采用电动刹车系统来代替传统的液压刹车系统.1983年至1986年期间,Goodyear Aerospace公司连续发表了多项电驱动飞机刹车的专利[5-9],其第一份专利考虑了采用磁粉来实现刹车压力盘和刹车盘的离合,随后的专利设计基本确定该电动刹车机构由电机、减速齿轮、滚珠丝杠、压力盘和刹车盘组成.其中,电机作为该电驱动系统的关键部件,同时还需要兼顾航空设备对可靠性和功率密度的基本需求,需要对电机的类型进行选择.文献[10]针对几种典型电机的动力学特性进行了总结,如交流电机、磁阻电机、永磁电机,如表1所示.由此可见,永磁电机具有很高的功率密度,可以提供足够的转矩满足飞机刹车的需求,同时容错性高、效率高、扭矩波动低,是电驱动刹车系统最佳选择之一.

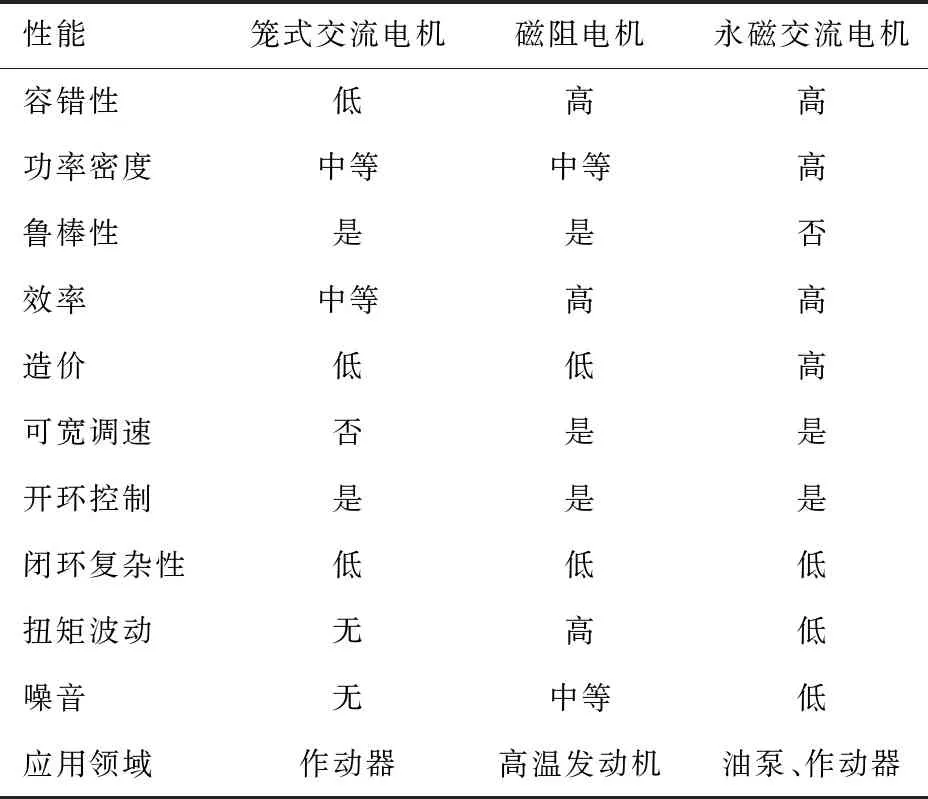
表1 多电飞机电驱动作动器不同电机动力学特性对比

1988年,该电动飞机刹车在A-10飞机平台上进行了测试,该试验将原液压刹车器拆卸下来后直接换上了待测试的电动刹车器,在安装有动压仪的测试台上进行了各种刹车类型的测试[11].测试中发现,由于该电动刹车的滚珠丝杠效率低,导致刹车的锁紧力相较于液压刹车略差,但是电动刹车的刹车力矩控制更精确,从而使得防滑测试中刹车距离更短.此次测试证明了所设计的电动飞机刹车的可行性,并以此设计框架为基础,根据该系统的动力学特性进行优化设计的探索.

本文对多电/全电飞机的发展历程以及对社会产生的深远影响进行了概述,从而引出研究电驱动刹车系统的重要性,介绍了当前民用飞机电驱动刹车系统的主要组成,对各子系统的动力学建模方式进行总结与比较,探讨电驱动刹车系统存在的不连续外激励力与交互不连续性可能产生的系统动力学行为,提出目前研究成果存在的不足及未来研究应集中的方向,以期望对民用飞机电驱动刹车的动力学设计与控制提供更全面的理论支撑.

1 电驱动刹车动力源建模与特性分析

电机作为飞机电驱动刹车系统的主要动力来源,其中直流无刷电机因其具有驱动响应快、高容错性等优势被普遍采用.1992年文献[12]给出了三相直流无刷电机的动力学模型,并采用Park变换推导了其在交直坐标系下的表达式,如式(1)和式(2)所示.

(1)

(2)

式中:i1、i2和i3分别为电机的三相电流;v1、v2和v3分别为电机三相输入电压;i1和id分别为直轴和交轴上的电流;vq和vd分别为直轴和交轴上的输入电压;L为电机绕组的自感和互感矩阵;Lq和Ld分别为电机绕组等效在直轴和交轴的电感;n为电机的极对数;Ke代表电动势,如反电动势等;R为电机线圈的电阻;ω为电机转子的转速.

针对不同电机转速,通过式(2)可计算出直流无刷电机直轴和交轴上的稳态电流,并通过式(3)计算出电机的电磁扭矩Te,如下式:

(3)

当电机气隙均匀时,电磁转矩Te可以改写为如下式所示:

(4)

1.1 转矩脉动与控制

直流无刷电机的转矩脉动成因主要是齿槽转矩、反电动势波形缺陷、电流波动、相电流换向等.直流无刷电机的各相输入电压由逆变器所控制,外接直流电源经过逆变器,并通过特定的切换规则将恒定电压转变为矩形波的交流电输入到各相,图1给出一种典型的三相逆变电路.文献[13]首次解析地分析了相位换向对直流无刷电机转矩脉动影响的规律,发现当电机电流得到有效控制时转矩波动与电机转速有关,低速时转矩会增大至正常转矩的1.5倍,而高速时转矩则会减小至正常转矩的一半,如图2所示.文献[14]给出了直流无刷电机气隙磁场和转矩的解析计算方法,其计算结果和有限元方法的结果十分吻合,可以用于针对换向引起的直流无刷电机转矩脉动分析.

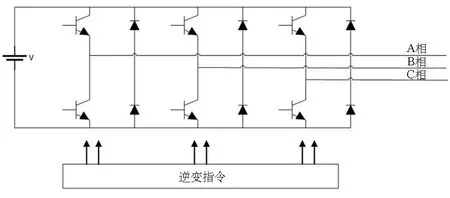
图1 三相逆变电路示意图Fig.1 Illustration of three-phase inverter circuit

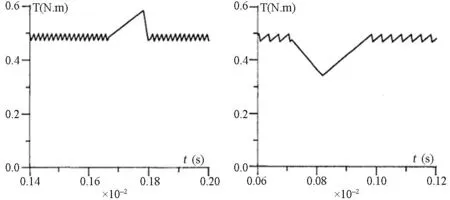
图2 换向对电机转矩脉动的影响[13]Fig.2 Influence on the toque ripple of the motor due to commutation[13]

为了降低转矩脉动从而提高直流无刷电机的工作效率,文献[14]提出可以将电机的反电动势设计成梯形波或者合理设计引入一定的馈电流谐波,使得反电动势和电流的乘积尽量保持恒定.沿着该思路,文献[15]提出合适的驱动电路模型可以直接影响直流无刷电机的转矩脉动强度,并将电机工作转速-平均转矩图划分为三个区域,不同区域的分界线可以解析地获得,证明了区域三电机的转矩脉动最小,从而指导驱动电路模型的设计.文献[16]还提出使用电流查找表的方式,通过实时检测电机的转角和转速来确定三相电流的期望值,如图3所示.文献[17]在该控制流程图的启发下,提出了在交直坐标系中求解直轴所需的电流,并通过Park反变换得到三相电流的期望值,这样可以将零转矩脉动控制变得更加简易.Chung等[18]利用模型参考自适应控制技术对无刷直流电机的链路磁通进行估计,再使用变结构的空间矢量脉宽调制法实现对电机转矩的实时控制,使得电机在低转速工作时的转矩脉动得到了有效降低.Song和Choy[19]提出了一种基于单直流电流传感器的直流无刷电机转矩脉动的抑制方法,该方法设计了无差拍电流控制器来提高电流控制的性能.文献[20]针对正常传导和换相阶段,推导了控制晶体管电压的占空比解析表达式,以此规则控制直流无刷电机可以有效减小电机的转矩脉动,同时该方法还考虑了直流供应电源存在上限的情况,并给出了相应的转矩脉动抑制解决方案.在过去十年,涌现了许多研究致力于如何解决直流无刷电机的转矩脉动抑制问题,并提出了许多经过试验验证的控制方法,如调节换相速度法[21]、基于向量的电流调节法[22]、缩减换相时间法[23,24]、谐波电流注入法[25]、电压供应端电容设计法[26,27]等.此外,文献[28]提出在输入电压端新增一个含丘克(Cuk)电压增益的直流-直流转换器,以此来降低相电流波动从而稳定转矩.以上研究仅针对直流无刷电机在恒定负载下的产生转矩脉动该如何设计控制方法,而飞机电驱动刹车系统在非常短的刹车过程中负载会产生复杂变化,并且变化的速度非常快.在这种复杂工况下,作为刹车主要控制源的直流无刷电机如果产生转矩脉动,会对整个刹车系统产生什么影响、控制是否需要进一步改进仍有待进一步研究.

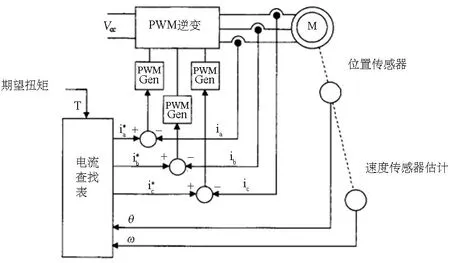
图3 最优电流激励实现图[16]Fig.3 Implementation of optimal current excitation[16]

1.2 非理想状态及故障建模与分析

直流无刷电机故障主要可以划分为以下四类[29]:电源开关开路、电源开关短路、直流链电容短路和霍尔传感器故障.其中前三种故障直接改变了直流无刷电机的电路结构,仅需要根据实际电路状态重新建模即可.由霍尔传感器控制的直流无刷电机相较于无传感器控制技术,结构简单且易于实现,因此被广泛应用.为了实时探测电机转子的位置从而给定相应的换相指令,三个霍尔传感器的放置必须严格按照120度的间隔分开,一旦放置存在偏差将导致电机各相的传导时长不一致,从而增大直流无刷电机的转矩脉动、振动和噪声,降低电机的整体机电性能.

文献[30]和文献[31]指出中、低成本的电机可能会有霍尔传感器分布不均的情况,他们通过测量同一个传感器连续四次切换的实际角位移,并对其做平均,通过类似的手段得到一个时间常数从而可以计算出电机的平均转速,同时对每一相的切换时间进行更新.通过这种滤波的方式对换相时间进行修改,可以有效应对霍尔传感器分布不均匀所造成的直流无刷电机转矩脉动,修正后的转矩曲线比较接近理想情况,并且这种方法从算法实现上比较容易.Alaeinovin等[32]分析了霍尔传感器错位引起的定子电流和转矩的变化,并提出了一种通过反电动势来测量霍尔传感器位置与理想位置偏差角度的测量方法.其后,Alaeinovin等[33]在文献[31]的基础上继续进行研究,他们提出一种新的滤波方式,针对微控制器输入霍尔传感器的触发信号,经过计算推导出时间修正因子,并输出更新后的触发信号,根据该信号来控制直流无刷电机的换相.文献[34]在直流无刷电机匀速运行的假设条件下,推导了霍尔传感器错位信号补偿量的计算模型,但该补偿方法需要在角度控制作用下才能有好的效果.相比在线补偿方法,离线补偿方法不需要额外的直流电流和电压传感器或者复杂的控制算法,文献[35]提出了一种直流无刷电机存在霍尔传感器错位情况下的离线补偿方法,将霍尔信号进行重组用于电机的换相控制.文献[36]指出霍尔传感器错位不仅会引起直流无刷电机的故障运行,并且由于阈值设置的影响,霍尔传感器还存在不均匀的霍尔信号误差.以上研究都针对直流无刷电机存在霍尔传感器错位的故障问题提出了改进方法,但是所提出的方法都假设电机的转速恒定.然而,飞机电驱动系统的直流无刷电机工作时转速并不恒定,其转速时域图通常呈现类似方波的形式,如图4所示.如果所采用的直流无刷电机存在霍尔传感器错位故障,对整个刹车过程和控制系统的影响还有待深入研究.此外,考虑直流无刷电机转速不恒定,设计一种霍尔传感器错位补偿方法存在很大的挑战.

图4 飞机刹车电机转速曲线[37]Fig.4 Motor speed curve during the brake process of aircraf[37]

2 减速齿轮子系统动力学特性

齿轮传动是一种典型的传递运动和动力的装置,也是飞机电驱动刹车系统的关键环节,它将直流无刷电机输出轴的旋转速度降低,使得滚珠丝杠接收到足够的扭矩用于挤压刹车片.模拟齿轮传动系统的动力学特性可以通过集总参数法、有限元法等来实现,其中基于集总参数法建立的齿轮传动动力学模型计算效率高,被广泛应用于该系统的动力学与控制研究.Wang[38]提出采用线性微分方程来描述齿轮的运动,模型中没有对齿轮啮合力进行直接建模,而是假设啮合力作用到两个齿轮上的扭矩相等、大小相反,并引入齿轮副效率来减少该假设所引起的建模误差.Harris[39]在模型中考虑了齿轮间的啮合力和摩擦,并根据试验结果给出了齿轮啮合力模型的两种形式:(1)刚度恒定的线性弹力和周期误差;(2)静态误差加动态刚度的线性弹力,该动态刚度采用了方波函数来模拟.文献[40]针对多级齿轮组建立了考虑齿轮传递误差的非线性动力学模型,模型中齿轮间的啮合刚度被看作是固定不变的参数.文献[41]建立了描述齿轮侧隙的数学模型,该模型考虑了齿轮在侧隙中运动时的空程运动以及啮合力加载、卸载产生的滞回环效应,如式(5)所示.

(5)

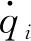
传动误差是由于齿轮的几何缺陷、齿间接触时的弹性形变、支撑结构的弹性形变或安装误差等所导致,通常采用角度差TE(θ)或线位移差TE(d)来度量,如式(6)所示.文献[42]总结了传动误差的几种计算方法,包括解析法、数值法和解析-数值法,并且讨论了如何测量和降低传动误差.

(6)

式中:θp和θg为两齿轮的角位移;Rbp和Rbg为两齿轮的半径.

相较于文献[39]中将齿轮啮合的动态刚度简单地描述为方波形式,文献[43]采用傅里叶级数给出了考虑齿轮静态传动误差的动态啮合刚度表达式,并在小参数的假设下研究了齿轮副系统在周期变化的啮合刚度和侧隙作用下的非线性动力学行为.但是该研究没有讨论如何根据齿轮的几何形状和材料属性来计算啮合刚度模型中的傅里叶系数,并且小参数的假设对实际应用也具有一定的局限性.文献[44]同时考虑了赫兹接触、弯曲、剪切和轴向压缩,分别计算上述因素对应的刚度系数,再采用弹簧串联的原理计算最终的等效刚度.当存在两对齿啮合时,将第二对啮合的齿的刚度模型串联进来,计算出该过程的等效刚度.因为齿轮副在啮合过程中啮合角在变化,并且会在一对和两对齿同时啮合这两种情况下交替运动,因此所计算得到的等效啮合刚度呈现出如图5的形式.基于该模型,更多的特殊情况得到了考虑并应用到研究该工况下的齿轮动力学特性的案例中,如齿轮裂纹[46-48]、齿轮修形[49,50]、剥落缺陷[51,52]等,其中关于齿轮裂纹对时变啮合刚度计算模型建立的研究工作居多.

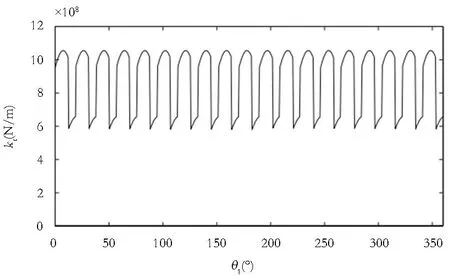
图5 齿轮有效啮合刚度计算结果图[45]Fig.5 The computation result of the effective mesh stiffness of the gear-pair[45]

当齿轮侧隙和输入输出扭矩存在波动同时存在时,齿轮系统可能在运动过程中出现拍击振动,会影响飞机电驱动刹车系统的控制效果,并且拍击振动还会产生噪音.文献[53]指出侧隙存在于所有的齿轮系统中,由于该因素引起的齿轮碰撞振动或拍击问题,需要进行深入研究.描述齿轮在侧隙区间无啮合运动的死区模型在该文献中得到了描述,并至今被广泛采用,该研究还从齿轮相对线位移、从动齿轮角加速度和驱动齿轮角加速度三个方面,分别给出了评判齿轮系统是否会出现拍击振动的准则.文献[54]除了考虑因侧隙而引入的死区模型以外,还加入了齿轮从侧隙区域的自由运动转为齿间啮合时的碰撞运动,并利用动量定理单独建立了齿间碰撞状态下的动力学模型,研究了存在侧隙的齿轮系统在波动扭矩作用下的周期运动和流擦边现象.在文献[54]研究的基础上,文献[55]还建模了齿轮啮合的过程,采用流转换复杂性理论分析了齿轮系统齿间碰撞作用力系数变化引起的分叉,但该模型的啮合刚度没有考虑时变因素.文献[56]采用打靶法得到了一类单自由度齿轮系统的不稳定周期运动轨道,并采用OGY方法实现了该系统的混沌控制.文献[57]针对行星齿轮动力学系统的间隙、摩擦、时变啮合刚度等引入的非线性,提出了通过修形来主动降低该齿轮系统运动过程中的振动噪声问题.除了齿轮侧隙的存在会导致齿轮系统在波动扭矩作用下出现拍击振动外,最近有研究发现齿轮润滑的油膜力也会对拍击振动产生影响[58-60],文献[59]发现随着油膜厚度的增长,文献[60]引入了纳维-斯托克斯方程来模拟油膜产生的润滑力,并比较了六种典型模型在不同润滑状态下的计算效果.为了更直观地展示齿轮系统在发生拍击振动的过程中的齿轮状态,文献[61]采用高速相机清楚地捕捉到了齿轮运动过程中存在齿间完全不接触的空程运动(如图6所示),为以往提出的死区模型提供了试验证据.文献[62]针对存在侧隙的齿轮系统给出了其分段线性模型的解析解,并详细地给出了齿轮系统无碰撞、单边碰撞和双边碰撞运动的工况边界,发现随着外力的变化,系统会产生复杂的混沌分叉现象.综上可知,齿轮系统存在时变啮合刚度、接触力不连续等非线性特征,在外界动态激励的作用下会产生拍击、混沌等复杂非线性行为.

图6 基于高速相机的齿轮接触可视化[61]Fig.6 Visualization of the contact zone of the gears with high speed camera[61]

作为飞机电驱动刹车系统中的重要传动环节之一,齿轮系统输入端将电机的高转速降低,输出足够大的扭矩从而实现飞机刹车,运动过程中齿轮转速变化复杂且剧烈,平均输出扭矩非常大,在这种恶劣工况下齿轮系统的拍击振动产生的动力学规律还未见有研究,拍击振动对刹车性能的影响还需要深入分析.另外,在波动大负载的作用下,齿轮系统可能会出现裂纹,齿轮裂纹对飞机电驱动刹车系统的动力学和可靠性会产生什么影响,是多电/全电飞机安全性评估的关键.

3 滚珠丝杠子系统分析

作为将飞机电驱动刹车系统前部分的旋转运动转换为直线运动,从而推动刹车压力盘挤压刹车片产生刹车力矩的重要装置,滚珠丝杠的螺杆输入力矩和螺母所受挤压力都相当大,如果用表示螺杆转角和螺母位移的简单表达式来模拟该部分的动力学行为会产生一定的偏差.

文献[63]基于集中质量法,并结合拉格朗日定理推导出了滚珠丝杠进给系统的动力学模型,如式(7)所示.所建立的模型可用于分析滚珠丝杠给进系统的动态响应,试验结果显示在工作台和固定平台所测得的系统特征频率前四阶与模型计算出的特征频率偏差均低于5%,并且还发现第1阶特征频率均存在于其他集中质量的振动中,是影响滚珠丝杠系统动态特性的主要因素.除此之外,螺母的位置也会影响滚珠丝杠系统的特征频率,其振动可能会通过电机的速度反馈引入控制回路,从而导致系统的不稳定.

(7)

式中:θs、xs和xT分别为螺杆的角位移和线位移、工作台的线位移;Is和ms分别为螺杆的等效转动惯量和等效质量;mT为工作台的质量;ξrs、ξss和ξT分别为螺杆的转动阻尼、螺杆与驱动端以及工作台与螺母联接的横向振动阻尼;p为螺杆的导程;kn和ks分别为螺母与工作台、螺杆与固定平台之间的联接刚度;Ts为滚珠丝杠系统的驱动力矩;Fe为工作台所受到的反推力.

文献[64]和文献[65]将滚珠丝杠系统进行了整体等效,针对性地建立了与滚珠丝杠联接的工作台在重载作用下的振动模型.螺母与工作台之间的联接被假设为刚性联接,因此工作台振动造成工作台相对于平衡位置的位移将对滚珠产生挤压,从而将挤压产生的弹性力直接作用到工作台上.基于赫兹理论,分析螺母、滚珠和丝杆所产生的弹性形变力,可以将工作台与滚珠丝杠之间的等效刚度计算出来.对于该等效刚度,文献[64]建立了刚度与摩擦力、螺母位置、螺杆导程和螺杆张力相关的函数式,用于研究滚珠丝杠系统线性运动端进给速度对系统特征频率和各联接刚度的影响规律,进给速度增大会降低系统的特征频率,同时当速度达到一定值时滚珠丝杠系统和驱动装置联接的远端轴承支承刚度会陡降为零.文献[65]建立了刚度与外载荷加速度、工作台质量、螺母位置和螺杆张力相关的函数式,并发现外载荷加速度也会影响滚珠丝杠系统中的联接刚度和特征频率,当外载荷加速度达到一定数值时,螺母与滚珠联接、轴承联接点的刚度甚至为降为零,使得滚珠丝杠系统发生严重的失稳现象.文献[66]在此基础上引入了联接的非线性,螺母与工作台之间的联接仍然被看作是刚性联接,但是将滚珠丝杠作用到工作台上的力不再使用线性弹簧模型来模拟,经过推导该作用力可以用一个分段非线性奇函数来表达,可以近似地采用线性弹簧和三次非线性弹簧来模拟.

滚珠丝杠预载是决定系统运行性能的关键参数之一,预载太低会引起振动问题,从而导致滚珠丝杠螺母的位置控制精度,预载太高又会增大滚珠丝杠内部运动的摩擦,引起系统工作温度的升高,同样对滚珠丝杠的工作性能带来负面影响.文献[67]指出考虑预载情况下的滚珠丝杠系统,可以用如式(8)的经验公式来更新螺母与工作台之间的联接刚度,公式中的参数需要通过试验获得,一般会由滚珠丝杠生产厂商提供.研究发现通过增加预载可以有效提高滚珠丝杠系统的特征频率,特别地对第1阶特征频率影响最大,利用此规律可以通过螺母的振动信号来监测和诊断滚珠丝杠系统的健康状态.不同于考虑滚珠丝杠螺母的预载,文献[68]讨论了螺杆预载情况下丝杠螺母系统的动力学特性,并得出如下结论:(1)螺杆的预载增加使得轴承的预载线性增加,但螺母的预载会降低直至为零;(2)螺杆的预载过大会导致螺母与工作台的联接失效,增加螺母的预载可以提高使其失效的螺杆预载临界值;(3)螺母的长度会改变螺杆预载影响螺母刚度的变化趋势.因此,如何实时监控滚珠丝杠的预载损失成为了最近的研究热点之一[69,70].

(8)

式中:P为滚珠丝杠的预载等级;C为动载荷等级.

4 子系统交互与不连续性分析

飞机电驱动刹车系统结构复杂,通常包含直流无刷电机、减速齿轮、滚珠丝杠、压力盘和刹车片等子系统.直流无刷电机输出轴与减速齿轮的主动齿轮输入轴、减速齿轮输出轴与滚珠丝杠螺杆通过弹性联轴器进行联接,滚珠丝杠螺母与压力盘通过工作台进行刚性联接,压力盘与刹车片之间存在间隙并且挤压刚度模型具有高阶非线性特征,是由多个刚体通过联接组成的多体系统.由前面章节可以看出,各个子系统都具有复杂的非线性动力学特性,并且减速齿轮和滚珠丝杠等都存在间隙和摩擦因素,这些会给整个刹车系统引入不连续性,使得减速齿轮的主动齿轮与从动齿轮运动过程中的交互作用力存在不连续性,滚珠丝杠螺母与工作台交互运动过程中产生的作用力也存在不连续性.在飞机刹车过程中,电驱动刹车系统外载荷为快时变、高幅值的刹车力矩,在这种特殊工况下飞机电驱动刹车系统的动力学行为会变得相当复杂.

1983年,Shaw和Holmes[71]利用映射技术研究了分段线性不连续系统的动力学行为.Pfeiffer[72,73]给出了齿轮传动的碰撞模型,并从理论和实验两个方面分析了齿轮箱出现的常规运动与混沌现象.针对含对称三线性弹簧的分段线性系统,Natsiavas[74]通过改变初始条件研究了该系统周期运动的稳定性和分叉.基于分段线性模型,齿轮传动系统动力学得以被深入分析[43,75].接着,Kleczka[76]进一步讨论了分段线性系统的周期运动和分叉行为.Luo和Menon[77]通过映射结构研究了周期激励作用下的分段线性系统出现的全局混沌运动,并且对该周期运动进行了解析预测.为了模拟齿轮传动系统的振动,Luo和Chen[78,79]建立了一个含碰撞的分段线性模型,发现了周期运动的擦边行为和混沌运动,并通过局部奇异性理论讨论了该系统奇异分形的擦边机理.在上述研究中,他们均假设齿轮副在同一个位置发生塑性碰撞.2009年,Luo和O’Connor[80]认为齿轮副的两个子系统应该是独立的,因此碰撞可能发生在不同的位置,并建立了一个包含多个子系统的碰撞模型.为了降低齿轮传动系统的噪声,Novak[81]在齿轮传动机械模型中引入了扭转和轴向间隙的影响,通过对该模型的研究他发现了齿轮传动系统存在的粘滞运动.为了进一步探索该系统粘滞运动和碰撞颤振产生的机理,Luo和O’Connor[82]提出了含粘滞运动和不含粘滞运动的周期颤振解析预测的方法,并且讨论了齿轮传动系统在交互不连续作用下的全局非线性行为.车辆悬架系统也由多个子系统组成,因为碰撞产生了系统交互的不连续.Kaiser[83]将其简化为一个含干摩擦的分段线性模型,并针对该系统的粘滑现象进行了参数分析.随后,Chandiramani[84]对该系统的粘滑动力学进行了实验研究.Wu和Yang[85]研究了列车穿越简支桥梁时,由于悬架子系统之间的碰撞而产生的动力学响应.除了以上关于齿轮传动系统和车辆悬架系统因碰撞产生交互不连续的动力学研究以外,闵富红[86,87]通过设计两个动力学系统的交互规则,实现了系统同步的目的,并在二维参数图中给出了不同步、部分同步和完全同步运动的分布域.傅希林[88,89]基于局部奇异性理论研究了Van der Pol系统的碰撞和动力学振荡,以及螺栓-螺帽二体系统在碰撞和摩擦作用下的流可转换性机理.范进军[90]基于局部奇异性理论研究了约束碰撞产生了系统交互的三自由度非线性振子,并得到了系统含粘滞的周期运动.傅希林和黄健哲[91]基于局部奇异性理论,针对无人飞行器在不连续交互控制作用下可能发生的运动颤振进行了机理分析,并提出一种颤振预警模型.

飞机电驱动刹车系统因碰撞和摩擦而产生的子系统交互不连续,由于不连续边界的函数表达式包含相关子系统的运动状态,因此该不连续边界随着子系统的运动在状态空间中随时间变化,该复杂非线性多体系统的流在时变边界和棱上的切换机理还需要通过深入研究来厘清.另外飞机在刹车过程中,电驱动刹车系统所受的外激励力并非恒定,并且变化速度和加速度都会很大,在这种复杂激励作用下飞机电驱动刹车系统会产生怎样的非线性动力学行为值得进一步研究.

5 结论

飞机电驱动刹车系统是一个由多个非线性刚性子系统组成的机电耦合多体系统,子系统之间存在系统交互和不连续性等基础问题,不同领域的学者针对各个子系统和系统交互不连续引起的非线性动力学行为开展了广泛深入的研究.通过对相关国内外研究进行归纳,波动外激励以及系统内部存在缺陷、间隙和摩擦时,都会对子系统的工作性能产生明显影响,对子系统的动力学影响规律都有统一认识.在前期的研究基础之上,飞机电驱动刹车系统在以下几个方面仍需进一步研究.

(1)直流无刷电机会因为非理想换相状态产生电磁转矩波动,霍尔传感器放置的位置分布不均匀会使波动加剧,飞机刹车过程中电机转子在外部波动负载和电磁转矩脉动共同作用下的非线性动力学行为还需进行研究,另外此前针对直流无刷电机电磁转矩脉动抑制的研究都是基于恒定转速的假设下设计的,而飞机刹车过程中电机的转速并不恒定,而且波动很大,如何设计新的控制方法抑制直流无刷电机的电磁转矩脉动,提出电驱动刹车系统的低振动设计方案值得研究.

(2)飞机电驱动刹车系统是一个多体系统,多刚体之间接触可能存在间隙,如从动齿轮与驱动齿轮之间、滚珠丝杠螺杆与螺母之间、压力盘与刹车片之间等,这些间隙会随着刚体之间的相对运动随时间变化,同时电驱动刹车系统中刚体之间接触而产生运动交互,交互过程又因为间隙而存在不连续性,针对这种特殊的不连续多体动力学系统,控制系统流的向量场在时变不连续边界上转换的机理还不清楚,流转换所引起的分叉行为还需要进行深入研究.

(3)飞机电驱动刹车系统中,不管在直流无刷电机中,减速齿轮中还是在滚珠丝杠中都存在摩擦,目前相关的研究还没有针对摩擦对电驱动刹车系统动力学特性的影响规律进行归纳总结,揭示摩擦与电驱动刹车系统在飞机刹车性能的内联机制,对于提高电刹车系统动力学特性的认识十分重要.

(4)飞机刹车过程中需要电驱动刹车系统提供非常高的刹车力矩,因此电驱动刹车系统所承受的负载特别大,并且随着飞机的滑跑速度、轮胎与地面接触的滑移率变化负载也随时间变化,目前针对飞机电驱动刹车系统所建立的动力学模型都是连续的,当系统存在不连续性时在复杂刹车工况情况下刹车系统动力学影响机制还不十分明确,目前已知各子系统存在不连续性时,在外部负载波动时会产生抖振,会增大系统的振动、降低系统的性能,甚至会导致系统的局部失效,但是各子系统产生耦合运动时不连续性和大负载波动对电驱动刹车系统的动态响应会产生什么影响值得研究.