简谐振动初相位之唯一性浅谈*
张国策 聂磊 陈云
(海南大学 土木建筑工程学院,海口 570228)
引言
振动在土木建筑、国防军工、道路桥梁、防震减灾等工程领域相当重要.根据激励性质不同,机械振动可分为固有振动[1,2]、自由振动[3,4]、受迫振动[5,6]、自激振动[7,8]和参数振动[9,10].简谐运动是最常见的振动形式.振幅、频率和相位是简谐振动的三要素.众多参考书介绍振动响应时,初相位常常需要被修正[11-27].
对于线性振动微分方程,一般可以精确求解.求解过程中,先构造振动响应的形式解;然后结合初始条件,分别求得振幅、频率和初相位.在求相位角时,通常先求出初相位的正弦值与余弦值,进而将初相位表示成已知参数组合的反三角函数.但是,反三角函数的值域与初相位的取值范围往往不一致.如果不注意值域,对于特定的系统参数组合,将可能导致与实际情况完全不符的振动响应.此类问题层出不穷,需要重视.
下面以单自由度振动系统为例,分别研究自由振动和受迫振动,在半开半闭区间(-π,π]内就初相位唯一性作简要论述.
1 自由振动
单自由度无阻尼系统自由振动是最基本的振动现象.以单自由度质量-弹簧系统构成的简谐振子为研究对象,质量块偏离平衡位置的距离x随时间t变化的规律满足如下微分方程:
(1)
式中,m表征质量块的质量,k表征弹簧刚度,两者取值均为正数.
胡海岩[16]等指出,自由振动控制方程(1)的形式解可写作:
x(t)=Asin(ω0t+α)
(2)
式中,固有圆频率:
(3)
考虑如下初始条件:
(4)
将式(2)代入式(4)可得:
(5)
解之得振幅:
(6)
若初始速度非零,则可得初相位[11-25]:
(7)
事实上,式(7)限制了相位角的值域,其余弦值始终为正,这就要求初始速度的代数值大于零.只有当初始速度方向与位移x正方向一致时,式(7)才是正确的.因此,该相位角(7)不一定是原系统(1)的解.如果v0<0,那么初始速度方向与x正方向相反,相位角(7)将给出错误的结果.修正如下:
(8)
式中,f为分段函数:
(9)
显然,自由振动响应的初相位与初始条件密切相关.综上所述,自由振动系统(1)的响应为:
(10)
2 受迫振动
考虑黏性阻尼力,单自由度振动系统受简谐激励作用时的微分方程为:
(11)
式中,c表征黏性阻尼系数,h表征简谐激振力的幅值,ω表征简谐激振力的频率,三者取值均为正数.
闻邦椿等[17,19]指出,受迫振动稳态响应与初始条件无关,其形式解可写作:
x(t)=Bsin(ωt+β)
(12)
将式(12)代入式(11)可得:
(13)
解之得振幅:
(14)
稳态响应时的初相位为[16-27]
(15)
事实上,式(15)限制了相位角的值域,其余弦值始终为正,这就要求外激励频率必须足够小.只有当激励频率ω小于派生无阻尼系统(1)的固有频率时,式(15)才是正确的.这与实际振动条件不符.因此,该相位角(15)不一定是原系统(11)稳态响应时的初相位.如果外激励振动过快,激励频率较大,那么相位角(15)将给出错误的结果.
考虑到阻尼系数和激励频率的代数值均为正数,由式(13)可知,初相位的正弦值小于零.因此,修正相位角如下所示:
(16)
考虑初始条件(4),根据常微分方程理论,小阻尼情形时受迫振动系统(11)的响应为:


人参皂苷Rc还具有增强精子活力[43]、抑制固定应激引起的血浆皮质酮水平的增加[44]、剂量依赖性的镇痛[45]、预防骨质疏松[46]、抑制活化的肾成纤维细胞增殖、防治肾纤维化[47]、抑制非人参病原菌和人参锈腐病菌菌丝生长[48]、诱导CYP1A1 mRNA与蛋白表达[49]等作用,且其没有胚胎毒性[50]。
(17)
3 数值验证
为了使用龙格-库塔法进行数值计算,引入速度变量v(t),将振动方程(11)改写为如下微分方程组:
(18)
考虑如下参数组合:
c=h=0,m=1.0kg,k=1.0N/m
(19)
此时,系统(18)代表了单自由度无阻尼振动系统(1).特选取初始条件如下:
(20)
数值仿真过程中令时间步长为0.0001s,采样点为0.5s,计算结果如图1中蓝色实心圆点所示.
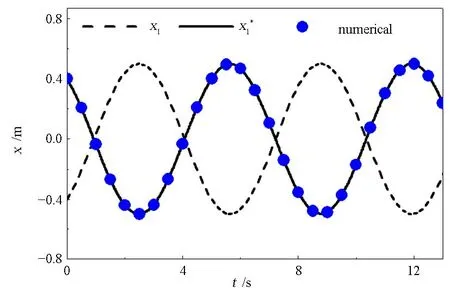
图1 自由振动周期响应Fig.1 The periodic response of free vibration
基于文献[11]~文献[25],由式(2,3,6,7)可得解析结果:
x1(t)≈0.5sin(t-53.1301°)m
(21)
因所选初始速度为负数,故需修正相位角.由式(2,3,6,8)可得改进结果:
(22)
再计算受迫振动系统,不妨考虑如下参数组合:
c=0.5N·s/m,m=1.0kg,k=1.0N/m
(23)
初始条件仍为式(20),特选取激励参数为:
h=0.4m,ω=1.2rad/s
(24)
仿真过程中令时间步长为0.0001s,采样点为0.5s,根据式(18)数值计算暂态响应如图2中红色实心圆点所示.图中实线代表小阻尼受迫振动系统的响应(17).两者完全重合.数值验证结果支持式(17)是有阻尼系统(11)的一个解析解.

图2 受迫振动暂态响应Fig.2 The transient response of forced vibration
随着计算时长变大,系统逐渐进入稳态.基于文献[16]~文献[27],由式(12,14,15)可得近似解析结果:
x2(t)≈0.5376sin(1.2t+53.7462°)m
(25)
因所选激励频率大于固有频率,故上式将给出错误的结果.修正相位角后,由式(12,14,16)可得改进结果.稳态响应近似为:
(26)
从图3示出了受迫振动稳态响应(25)与(26)的对比结果.图中虚线代表文献[16]~文献[27]中的响应解(25).实线代表改进结果(26),与数值仿真结果吻合.图例表明,相位角不同,将导致多数时刻振动响应计算结果偏离真实值.

图3 受迫振动稳态响应Fig.3 The steady-state response of forced vibration
4 结束语
相位角是简谐振动的三要素之一.分别考虑自由振动和受迫振动,给出了任意初始条件下系统响应的解析解.理论求解过程中,如果不注意反三角函数的值域,将可能导致与实际情况完全不符的振动响应.日常科研中应受到重视.
(1)无阻尼线性系统自由振动时,初相位与初始条件、固有频率均相关,且在区间(-π,π]内具有唯一性.
(2)线性阻尼系统受简谐激励时,稳态响应与初始条件无关,但相位角与激励频率、固有频率密切相关,且初相位在区间(-π,π]内具有唯一性.

