融合时序关联动态图与常微分方程的区域间出租车需求预测
王海程 马纪颖 张苑媛 杨绍祖
摘 要:为解决出租车行业中的高空驶率和不均衡的需求分布问题,通过对出租车出行的区域进行深入研究,提出了一个融合时序关联动态图与常微分方程的需求预测模型TCG-ODE(temporal correlation graphs-ordinary differential equations)。首先,模型使用ODE(ordinary differential equation)对图卷积神经网络(graph convolutional network,GCN)進行微分方程建模,将堆叠局部特征信息抽象为动态图,以节点的时序特性来推进局部节点状态;然后,设计了一种基于注意力分数调整采样策略的蒸馏方案,提高对多层稀疏图的适应效果,以更稳定地表征复杂时空特征,最终实现对区域间出租车需求量的预测。在真实的出租车订单数据集上进行实验,研究结果表明,TCG-ODE模型的预测效果均优于对照模型和改进前的模型。通过精准预测不同区域之间的出租车需求量,可以为出租车司机和乘客出行提供决策支持信息,从而优化供需关系。
关键词:需求预测; 图卷积神经网络; 常微分方程; 蒸馏方案
中图分类号:TP183 文献标志码:A
文章编号:1001-3695(2024)03-021-0794-05
doi:10.19734/j.issn.1001-3695.2023.06.0317
Inter-regional taxi demand forecasting based on time series correlationdynamic graph and ordinary differential equation
Wang Haicheng1,2, Ma Jiying1,2, Zhang Yuanyuan1,2, Yang Shaozu1,2
(1. School of Computer Science & Technology, Shenyang University of Chemical Technology, Shenyang 110142, China; 2. Liaoning Provincial Key Laboratory of Intelligent Technology of Chemical Process Industry, Shenyang 110142, China)
Abstract:In order to solve the problem of high vacancy rate and unbalanced demand distribution in the taxi industry, through in-depth research on the taxi travel region, this paper proposed a demand forecasting model combining temporal correlation dynamic graphs and ordinary differential equations,called TCG-ODE. Firstly, the model used ODE to model the differential equations of GCN, and abstracted the stacked local feature information into a dynamic graph. It advanced the local node state based on the timing characteristics of nodes. Then, it designed a distillation scheme based on the attention score adjustment sampling strategy to improve the adaptation effect to the multi-layer sparse graph, so as to more stably represent the complex spatio-temporal characteristics, and finally realized the prediction of inter-regional taxi demand. Experimental results conducted on real taxi order datasets demonstrate that the TCG-ODE model outperforms both benchmark models and the pre-improvement model in terms of demand prediction accuracy. By accurately forecasting taxi demand among different regions, this model provides decision support information for taxi drivers and passengers, thereby optimizing the supply-demand relationship.
Key words:demand forecasting; graph convolutional network(GCN); ordinary differential equation(ODE); distillation scheme
0 引言
出租车在城市交通中扮演着重要的角色,它们作为城市间交通连接的桥梁,发挥着重要的作用。然而,由于出租车与乘客间不均衡的供需分布,导致出租车空驶率高与乘客打车难的矛盾,进而可能造成交通拥堵,给整体交通流畅性带来负面影响。随着人们对于出租车的需求不断增加,这种问题会被不断放大。某些区域或时间段出租车供应过剩,导致出租车空驶率高,司机的收入受到影响;同时,其他区域或时间段出租车供应不足,乘客面临打车难的问题,出行效率降低,影响了乘客的工作生活安排。为有效解决上述问题,需要对区域间出租车需求量进行精确的预测,从而为出租车司机和乘客提供合理的出行方案,进而提高司机收入、改善乘客乘车体验以及增强交通系统的可靠性。
区域间出租车需求量预测问题作为交通流量预测的一种,是指在特定城市或地区内的不同区域之间,通过挖掘历史轨迹数据来预测未来某个时间段内(如小时、天等)的出租车需求数量。现有的交通流量预测方法主要分为统计方法模型、传统机器学习模型以及深度学习模型。早期的预测主要以统计方法为主,包括移动平均法、指数平滑法、线性回归模型(linear regression)和自回归积分移动平均模型(autoregressive integrated moving average,ARIMA)[1]等。然而,这些方法受限于历史数据中的模式和趋势的建模能力,并且难以处理复杂的非线性关系。为了克服这些限制,机器学习方法,如支持向量机[2]、人工神经网络[3]和决策树[4]等被引入到交通流量预测中。这些方法能够利用大量的历史数据来学习交通流量的模式和关系,并且在一定程度上捕捉非线性关系和复杂模式,但通常需要大量数据和计算资源,且模型的解释性较差。
近年来,基于深度学习和神经网络的方法在交通流量预测领域得到了广泛应用。Ku等人[5]和吕开云等人[6]分别采用循环神经网络(recurrent neural network,RNN)和长短期记忆神经网络(long short term memory,LSTM)进行预测,但RNN和LSTM仅仅考虑时间依赖关系,忽略了空间结构对预测结果的影响。卷积神经网络(convolutional neural network,CNN)[7]同时考虑了时间和空间两个因素并且取得了较好的结果,但是其空间依赖关系提取方法太过简单,在非规则图结构上的表现较弱;此外,CNN在处理图数据时受限于卷积核大小和层数,难以实现深层特征学习。为此,部分学者提出了GNN的预测方法,使用GNN对图结构数据进行有效学习。例如:陈柘等人[8]使用GCN对城市路网内路段的空间关系特征进行挖掘以提升预测效果;Xiao等人[9]利用一种新的时空图卷积网络(space-time graph convolutional network,STGCN),通过挖掘多视角数据中的潜在信息来进行预测并返回需求;Guo等人[10]使用基于注意力机制的时空图卷积网络(attention-based spatial-temporal graph convolutional network,ASTGCN),利用GCN的结构,结合注意力机制对时空图数据进行建模和分析。实验结果表明,上述模型在需求预测任务方面取得了不错的效果。
尽管GNN在处理图结构数据方面具有优势,但是随着模型具有更深的层次结构或者训练轮数的增加,往往会出现过度平滑的现象[11].,导致模型难以区分不同节点并学习到相似的节点表示。为了验证本文实验中是否存在过度平滑现象,使用了基于GCN和歷史数据的建模和预测方法,得到了如图1所示的结果。实验结果显示,随着模型层数的增加,预测效果不再理想;而随着训练轮数的增加,预测结果逐渐趋于稳定。这种平滑化现象可能会导致模型损失对节点间细微差异的感知能力,使得节点的表示趋向于聚集在相似的空间区域中。为了缓解过度平滑问题,研究人员提出了一些方法。其中,NODE是一种基于常微分方程理论的神经网络模型[12],它提供了更灵活和表现力更强的模型架构来捕捉节点之间的时间关系。另外,Zheng等人[13]基于GNN提出了时空图常微分方程网络(STGODE),通过利用基于张量的常微分方程(ODE)来捕捉时空动态,构建了更深层的网络结构,从而进一步提高了交通流量预测的效果。
虽然现有的研究[1~12]能够实现不错的交通流量预测效果,但是仍存在以下问题:
a)多网络层堆叠过程可能会导致训练结果过平滑。这种过度平滑化可能导致节点之间的差异性减小,降低网络对于复杂模式和图结构的表达能力,导致无法有效地区分不同类别或图中的细节信息。
b)对于空间临近性关注度不够。在GCN当中,通过聚合节点的邻居特征来更新节点的表示,如果忽视了空间临近性,可能会导致特征聚合过程中的失衡,距离较远的节点可能被不合理地聚合,而忽略了距离较近的节点的重要信息,从而影响模型的特征表达和预测能力。
c)现有的神经常微分方程对于动态图的构建是以构建动态邻接矩阵为主,而缺少以时序序列为特征关系的构建方案。
d)时空特性引起的稀疏性对模型的适应能力较差,在处理复杂的时空关系时面临较高的计算复杂度。
为解决上述问题,本文提出了一种基于TCG-ODE的需求预测方法。模型通过神经常微分方程(neural ordinary differential equation,NODE)和多注意力机制来实现精准的需求量预测,主要的工作如下:
a)在多网络层堆叠过程中,将GCN模型的静态图卷积操作替换为动态的节点(NODE)表示,将节点表示的更新过程从离散的静态操作转换为连续的动态过程。通过利用NODE的动力学性质,捕捉节点表达中更复杂的模式和非线性关系。
b)构建以时序序列关系为基础的动态图方案,通过堆叠多个动态节点表示的网络层,以节点的时序特性来逐步推进节点状态。
c)设计了一种基于注意力分数调整采样策略的蒸馏方案,根据当前各节点的注意力分数计算当前状态下的采样数量,实时地调整采样策略。
3 实验
3.1 数据集
本文所使用的实验数据是基于纽约市出租车和豪华轿车委员会(TLC)的行程记录数据,其中特定选取了黄色出租车的订单数据作为实验数据源。提取其中的车流量数据作为实验数据集,将各时刻的原始订单数据划分成时间间隔5 min的数据样本,即每个区域每小时收集12个样本数据。数据集描述如表1所示。
为了确保分析和建模的准确性和效率,对使用的数据进行了预处理,包括异常值检测和数据转换。在订单数据记录过程中,可能会受到设备故障、障碍物干扰等因素影响,导致出现记录异常的情况,因此剔除异常或者缺失的数据。另外,为了满足模型训练的需求,将现有的订单数据记录转换为统计数据,得到符合实验要求的数据形式。预处理后,对数据按照小时进行周期处理并标准化处理。为了找到最佳的模型参数并更准确地评估模型性能,将数据集按照3∶1∶1的比例划分为训练集、测试集和验证集。
3.2 实验设置
为了有效评估本文模型的预测性能,分别采用平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)以及平均绝对百分比误差(mean absolute percen-tage error,MAPE)作为实验的评价指标,其公式如式(10)~(12)所示,数值越小表示预测效果越好。
其中:N表示时间序列长度;Yi表示预测区域i在预测时间间隔内的真实值;Y^i表示预测区域i在预测时间间隔内的预测值。实验使用Python编程语言,模型的搭建基于PyTorch深度学习框架。具体的实验环境描述如表2所示。实验中,每次迭代训练中用于更新模型权重的样本数量(batch_size)设置为32,优化器采用Adam,损失函数为MSE。模型训练200个轮次,初始学习率为0.001。
3.3 实验与结果分析
3.3.1 不同模型对比实验
为了验证TCG-ODE模型的性能选择,采用以下基线模型进行对比:
a)ARIMA[1]是一种经典的时间序列分析方法,结合自回归、差分和移动平均技术,用于预测具有一定趋势和季节性特征的数据。
b)SVR(support vector regression)[2]是一种机器学习回归方法,利用支持向量机技术,适用于非线性关系的数据预测与建模。
c)LSTM[6]是一种循环神经网络,通过门控机制来捕获长期依赖关系,用于处理时间序列数据,可捕捉长期依赖关系。
d)STGCN[9]是一种深度学习模型,结合图卷积和时空信息,用于处理时空数据。
e)ASTGCN[10]结合图卷积和注意力机制,用于处理时空数据,强调关键节点和时序信息。
f)STTN[15,16]利用自注意力机制整合时空特征,用于时序数据建模,强调节点间复杂依赖关系。
将TCG-ODE模型与以上各基线模型在Taxi NYC上进行未来3小时的预测性能对比,实验结果如表3所示。根据评价指标可知,TCG-ODE模型的预测效果优于其他模型。
其中ARIMA、SVR和LSTM模型的效果最差,这是由于它们缺乏对于空间特征的建模;STGCN虽然从时空角度进行建模,却难以捕获复杂的时空依赖关系;STTN基于Transformer架构,能够利用自注意力机制有效地建模时空关系,实现对复杂时空序列数据的建模和预测;ASTGCN在STGCN的基础上引入注意力机制,能够有效捕捉时空图数据中的关联性和时序特征,从而提高时空序列数据的建模和预测能力,因此,STTN和ASTGCN都取得了不错的效果。然而,上述模型都是以离散图结构进行建模的,在堆叠多层图结构的过程中会产生平滑的现象,导致预测结果不理想。相比之下,TCG-ODE模型以时序序列为特征关系,构建动态图的神经常微分方程模型,并着重关注区域临近性,因此取得了更好的预测效果。
3.3.2 优化过程消融实验
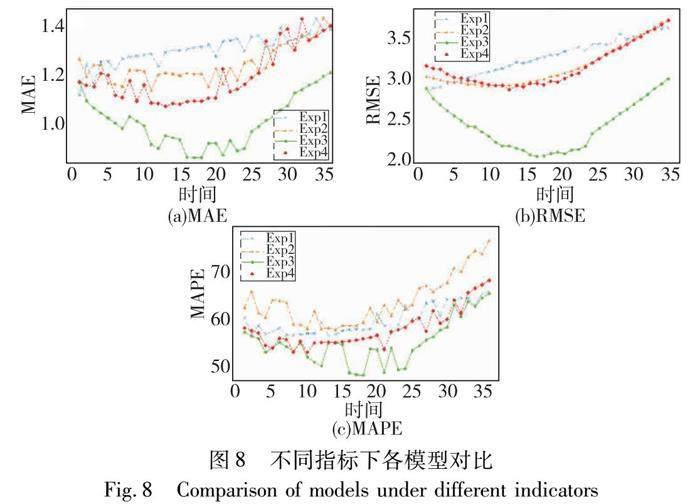
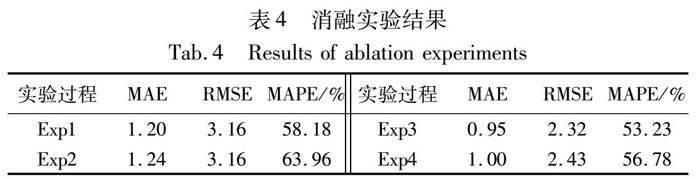
本文提出的预测模型是在STTN的基础上引入TCG-ODE层和自适应注意力层。为了验证上述两点对于模型性能的影响,消融实验分别在Exp1、Exp2、Exp3和Exp4模型上进行建模预测。其中:Exp1表示没有引入TCG-ODE层和自适应注意力层的模型;Exp2表示引入TCG-ODE层但没有自适应注意力层的模型;Exp3表示同时引入TCG-ODE层和自适应注意力层的模型,即TCG-ODE模型;Exp4表示引入TCG-ODE层中的TCG(temporal correlation graphs)模块和自适应注意力层的模型,它意味着对于多层图结构的离散建模过程。将上述模型进行消融实验,结果如表4所示。由表4可知,仅对于TCG-ODE层优化并不一定可以取得理想的效果,可能是由于模型对该数据的适应性不够好,在完成对自适应注意力层的优化后,提高了模型的泛化能力和对数据集的适应能力,所以预测效果均优于Exp1和Exp2模型;Exp4模型在预测过程中也取得不错的预测效果,但随着模型训练轮数增加,过平滑现象的出现导致了其预测效果不如Exp3模型。
为了进一步评估模型的预测性能,将预测未来3 h(36个时间间隔)的数据进一步可视化,为呈现全局预测趋势,绘制不同指标下的各模型对比图,如图8所示,分别展示了不同模型随着预测间隔增加,预测性能的变化。由图8可知,对于任一指标,Exp3(TCG-ODE)模型随着预测间隔的增加,预测性能均优于其他模型,而且变化相对稳定,这意味着相较于其他模型,Exp3在长时间跨度内可以保持可靠的预测性能。
3.3.3 真实值与预测值对比实验
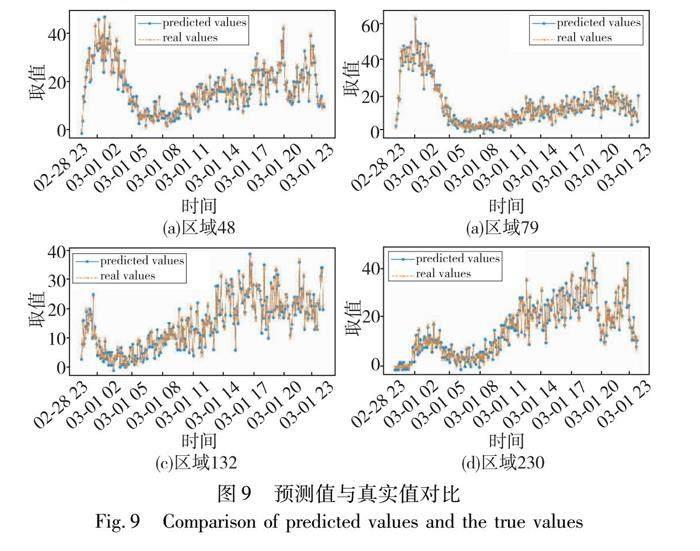
为直观地评估TCG-ODE模型的预测准确性和性能,将各区域间出租车数量预测值与真实值进行对比,以此量化模型在不同时间点的预测偏差,从而判断模型是否能够准确捕捉时间序列的变化趋势和波动。图9为不同区域在不同时序下的预测值和真实值比对的可视化结果。
从空间特征考虑,为体现比对实验的价值,从区域的多样性、挑战性和代表性出发,选择了编号为48、79、132和230的区域,这四个区域为纽约市不同区有代表性的区域;从时间特征考虑,为了较好地反映變化趋势,选择2023年3月1日一整天的时间进行预测对比。
通过对图9的观察可知,各个区域在时间内呈现出相似的趋势和波动,表明模型在捕捉时间变化方面相对准确。然而,在高峰或低谷时段的切换过程中,模型的预测值与真实值可能存在一些偏差,例如在早晨或下午的时间段,如图(a)和(b)在2~8点、图(c)在5~8点以及图(d)在8~17点,这种偏差可能源自于不同区域的交通、人流等因素差异,以及模型在不同时段的适应性表现。进一步观察,局部峰值的预测也可能存在一定程度的偏差,如图(a)和(b)在1~2点、图(c)在14~17点以及图(d)在16~18点,这可能是因为在这些时间点内,真实值受到特殊事件或外部因素的影响。虽然从时间角度来说,曲线变化的趋势和波动相似,但是不同区域之间的偏差变化是不同的,这暗示了每个区域的特定特征和模型的应对能力。在空间特征分析中,不同区域之间的差异引发了预测值与真实值的偏差变化,这反映了每个区域在不同时间段的特点和影响因素不同。综上所述,模型在预测时空特征方面取得了不错的效果,但是受外部因素、数据分布以及模型自身的限制影响,使得预测结果出现了一定的偏差。为了进一步提升预测精度,可以针对特殊时段和区域的特征进行更深入的分析,优化模型的参数和结构,并考虑引入更多外部数据来弥补预测误差。
s
4 结束语
本文提出了一种融合时序关联动态图与常微分方程的需求预测模型TCG-ODE,该模型以时序序列为特征关系,通过ODE对GCN进行微分方程建模,同时引入自适应注意力层,完成对区域间出租车需求量的预测。在真实的出租车数据集上进行实验,结果表明本文模型取得了不错的预测效果。然而,本文研究还存在一些局限性。首先,模型依赖于可靠的出租车订单数据,因此对数据质量和可用性有一定要求;其次,模型仍有进一步改进的空间,例如可考虑在更多的时空特征方面进行扩展;最后,受外部因素、数据分布以及模型自身的限制影响,预测准确度仍存在可以提升的可能。为减少局限性的影响,可以选择更高质量的数据进行实验,也可以针对特殊时段和区域的特征进行深入分析,以便更好地应对不同情况下的交通流量预测问题。综上,TCG-ODE模型在解决出租车行业中的空驶率高和需求不均衡问题方面表现出良好的预测效果,能为出租车行业的可持续发展和交通出行的优化提供参考和指导。
参考文献:
[1]刘学刚, 张腾飞, 韩印. 基于ARIMA模型的短时交通流预测研究[J]. 物流科技, 2019,42(12): 91-94,102. (Liu Xuegang, Zhang Tengfei, Han Yin. Research on short-term traffic flow forecast based on ARIMA model[J]. Logistics Sci-Tech, 2019,42(12):91-94,102.)
[2]曹来成, 梁浩, 韩薇, 等. 基于SVR对交通流中线性关联关系的分析与研究[J]. 计算机应用研究, 2015,32(2): 419-422. (Cao Laicheng, Liang Hao, Han Wei, et al. Analysis and research of linear correlation relationship in traffic flow based on SVR[J]. Application Research of Computers, 2015,32(2): 419-422.)
[3]田瑞杰, 张维石, 翟华伟. 基于时间序列与BP-ANN的短时交通流速度预测模型研究[J]. 计算机应用研究, 2019,36(11): 3262-3265,3329. (Tian Ruijie, Zhang Weishi, Zhai Huawei. Short-term traffic flow velocity prediction model based on time series and BP-ANN[J]. Application Research of Computers, 2019,36(11): 3262-3265,3329.)
[4]杨胜, 李莉, 胡福乔, 等. 基于决策树的城市短时交通流预测[J]. 计算机工程, 2005(8): 35-36. (Yang Sheng, Li Li, Hu Fuqiao, et al. Urban short-term traffic flow forecasting based on decision tree[J]. Computer Engineering, 2005(8):35-36.)
[5]Ku D G, Na S Y, Kim J Y, et al. Real-time taxi demand prediction using recurrent neural network[J]. Proceedings of the Institution of Civil Engineers-Municipal Engineer, 2021,174(2): 75-87.
[6]吕开云, 邱万锦, 龚循强, 等. 基于长短期记忆神经网络的城市交通速度预测[J]. 东华理工大学学报: 自然科学版, 2023,46(1): 77-84. (Lyu Kaiyun, Qiu Wanjin, Gong Xunqiang, et al. Urban traffic speed prediction based on long short-term memory neural network[J].Journal of Donghua University of Technology:Natural Science Edition, 2023,46(1): 77-84.)
[7]Ranjan N, Bhandari S, Zhao Hongping, et al. City-wide traffic congestion prediction based on CNN, LSTM and transpose CNN[J]. IEEE Access, 2020,8: 81606-81620.
[8]陳柘, 刘嘉华, 赵斌, 等. 基于GCN和TCN的多因素城市路网出租车需求预测[J]. 控制与决策, 2023,38(4): 1031-1038. (Chen Zhe, Liu Jiahua, Zhao Bin, et al. Taxi demand prediction of multi-factor urban road network based on GCN and TCN[J]. Control and Decision, 2023,38(4): 1031-1038.)
[9]Xiao Guangnian, Wang Ruinan, Zhang Chunqin, et al. Demand prediction for a public bike sharing program based on spatio-temporal graph convolutional networks[J]. Multimedia Tools and Applications, 2020,80(15): 22907-22925.
[10]Guo Shengnan, Lin Youfang, Feng Ning, et al. Attention based spatial temporal graph convolutional networks for traffic flow forecasting[C]//Proc of AAAI Conference on Artificial Intelligence. Palo Alto,CA: AAAI Press, 2019: 922-929.
[11]Chen Deli, Lin Yankai, Li Wei, et al. Measuring and relieving the over-smoothing problem for graph neural networks from the topological view[C]//Proc of AAAI Conference on Artificial Intelligence. Palo Alto,CA: AAAI Press, 2020: 3438-3445.
[12]Jin Ming, Zheng Yu, Li Y F, et al. Multivariate time series forecasting with dynamic graph neural ODEs[J]. IEEE Trans on Know-ledge and Data Engineering, 2022,35(9): 9168-9180.
[13]Zheng Fang, Long Qingqing, Song Guojie, et al. Spatial-temporal graph ODE networks for traffic flow forecasting[C]//Proc of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. New York: ACM Press, 2021: 364-373.
[14]Zhou Haoyi, Zhang Shanghang, Peng Jieqi, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[C]//Proc of the 35th Association for Advancement of Artificial Intel-ligence. Palo Alto,CA: AAAI Press, 2021: 11106-11115.
[15]Pu Bin,Liu Jiansong,Kang Yan,et al. MVSTT: a multiview spatial-temporal transformer network for traffic-flow forecasting.[J/OL]. IEEE Trans on Cybernetics.(2022-12-13). http://doi.org/10.1109/tcyb.2022.3223918.
[16]高榕, 萬以亮, 邵雄凯, 等. 面向改进的时空Transformer的交通流量预测模型[J]. 计算机工程与应用, 2023,59(7): 250-260. (Gao Rong, Wan Yiliang, Shao Xiongkai, et al. Traffic flow prediction model for improved spatio-temporal Transformer[J]. Computer Engineering and Application, 2023,59(7): 250-260.)

