关于不定方程x3-1=114y2

韩 帆,贺艳峰,李 勰

(延安大学 数学与计算机科学学院,陕西 延安 716000)

不定方程

x3-1=Dy2(D>0且无平方因子)

(1)

是一类重要的三次不定方程,其整数解的问题吸引许多专家学者去研究。例如,当D无形如6k+1的素因子时,不定方程(1)的全部整数解已由柯召等[1-2]给出,但当D含6k+1形状的素因子时,此方程的求解比较困难,即便如此,针对该方程解的研究也有很多成果。例如,当0100时的情况,只有一些零散的结果:杨晓柳等[12]证明了不定方程x3-1=229y2的整数解仅有(x,y)=(1,0);管训贵[13]证明了不定方程x3-1=511y2仅有整数解(x,y)=(1,0),(8,±1);宋晓禹等[14]证明了不定方程x3-1=749y2仅有整数解(x,y)=(1,0)。

本文在深入学习相关文献[15-23]的基础上,利用初等的数论方法证明了当D含有3以及6k+1型素因数时,不定方程x3-1=114y2仅有整数解(x,y)=(1,0)。

1 若干引理

引理1[24]设D是一个非平方的正整数,则Pell方程

x2-Dy2=1

(2)

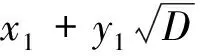
引理2[25]不定方程x4-3y2=1仅有整数解(x,y)=(±1,0)。

引理3[25]设p是一个奇素数,则方程4x4-py2=1除开p=3,x=y=1和p=7,x=2,y=3外,无其他的正整数解。

引理4同余方程x2+x+1≡0(mod 9)无整数解。

证明任意取x∈Z,当x≡0,8(mod 9)时,x2+x+1≡1(mod 9);当x≡1,4,7(mod 9)时,x2+x+1≡3(mod 9);当x≡2,6(mod 9)时,x2+x+1≡7(mod 9);当x≡3,5(mod 9)时,x2+x+1≡4(mod 9)。由此可见,原同余方程无解。

2 主要结果及证明

定理不定方程

x3-1=114y2

(3)

仅有整数解(x,y)=(1,0)。

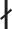
情形1:x-1=114a2,x2+x+1=b2,y=ab,gcd(a,b)=1;

情形2:x-1=2a2,x2+x+1=57b2,y=ab,

gcd(a,b)=1;

情形3:x-1=6a2,x2+x+1=19b2,y=ab,

gcd(a,b)=1;

情形4:x-1=38a2,x2+x+1=3b2,y=ab,

gcd(a,b)=1;

情形5:x-1=342a2,x2+x+1=3b2,y=3ab,

gcd(a,b)=1;

情形6:x-1=18a2,x2+x+1=57b2,y=3ab,

gcd(a,b)=1;

情形7:x-1=6a2,x2+x+1=171b2,y=3ab,

gcd(a,b)=1;

情形8:x-1=114a2,x2+x+1=9b2,y=3ab,

gcd(a,b)=1。

现在分别对这8种情形进行讨论:

情形1由第2式x2+x+1=b2可化为(2b)2-(2x+1)2=3,解此式,得x=0,-1,都不满足第1式,故该情形无不定方程(3)的整数解。

情形2对第1式取模8,因为a2≡0,1,4(mod 8),所以有x=2a2+1≡1,3(mod 8),代入第2式,有x2+x+1≡3,5(mod 8),从而有57b2≡3,5(mod 8),又因为x2+x+1=x(x+1)+1为奇数,则b也为奇数,此时b2=1(mod 8),推出57b2≡1(mod 8),进而1≡3,5(mod 8),但这不可能,故该情形无不定方程(3)的整数解。

情形3对第1式取模3,有x≡1(mod 3),代入第2式,则有0≡x2+x+1≡19b2(mod 3),推出3|b,因此x2+x+1≡0(mod 9),即(2x+1)2+3≡0(mod 9),但2x+1≡0(mod 3),即(2x+1)2≡0(mod 9),从而3≡0(mod 9),而这不可能,故该情形无不定方程(3)的整数解。

情形4由x2+x+1=3b2,得(2x+1)2+3=3(2b)2,将x-1=38a2代入,得(76a2+3)2+3=3(2b)2,所以3|a,令a=3c,得(2b)2-3(228c2+1)2=1,由引理1知Pell方程X2-3Y2=1的基本解为(2,1),故

易验证下列关系式成立:

xn+2=4xn+1-xn,x0=1,x1=2

(4)

yn+2=4yn+1-yn,y0=0,y1=1

(5)

xn+1=2xn+3yn,yn+1=xn+2yn

(6)

(7)

由yn=228c2+1,得yn≡1(mod 228),对递归序列(5)取模228,得周期为60的剩余序列,且当n≡1(mod 60),才有yn≡1(mod 228)。设n=60k+1,结合式(6)和(7)得

228c2=y60k + 1-1=x60k+ 2y60k-1

=2y30k(3y30k+ 2x30k)=2y30kx30k + 1

即 114c2=y30kx30k+1

(8)

又(y30k,x30k+1)=(y30k,3y30k+2x30k)=(y30k,2x30k)=2,因此式(8)必有下列情形之一成立:

x30k+1=76u2,y30k=6v2,c=2uv,gcd(u,v)=1

(9)

x30k+1=2u2,y30k=228v2,c=2uv,gcd(u,v)=1

(10)

x30k+1=4u2,y30k=114v2,c=2uv,gcd(u,v)=1

(11)

x30k+1=38u2,y30k=12v2,c=2uv,gcd(u,v)=1

(12)

对递归序列(4)分别取模4和38,得到x30k+1≢0(mod 4),x30k+1≢0(mod 38),因此式(11)和(12)中的第1式均不成立。

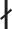
x15k=d2,y15k=3e2,v=de,gcd(d,e)=1

(13)

若式(13)成立,结合式(7),得

d4-3(3e2)2=1

(14)

由引理2知,式(14)仅有整数解(d,3e2)=(±1,0),此时y15k=0,则k=0,代入式(9)的第1式x30k+1=76u2中,有2=76u2,这显然不可能。

情形5将第1式代入第2式,得(2b)2-3(228a2+1)2=1,与情形4的讨论方法类似。

情形6对第1式取模8,由18≡2(mod 8),a2≡0,1,4(mod 8),则有x=18a2+1≡1,3(mod 8),代入第2式,有x2+x+1≡3,5(mod 8),即57b2≡3,5(mod 8),考虑到b2≡1(mod 8),则有57b2≡1(mod 8),从而1≡3,5(mod 8),但这不可能,故该情形无不定方程(3)的整数解。

针对情形7和8,分别对第2式取模9,根据引理4可知均不成立,故这两种情形无不定方程(3)的整数解。

综上所述,不定方程x2-1=114y2仅有整数解(x,y)=(1,0)。