“相交线与平行线”学习指导

王宗信

图形与几何的学习非常有趣，同时也是有规律的．通过数量关系可以判断图形的位置关系，反之，通过图形的位置关系也可以确定相应的数量关系．

一、认识相交线

（一）两条直线相交形成的四个角之间的关系

一条直线与另一条直线相交，形成四个小于平角的角．

1．邻补角．

如图1，D是直线AB上一点，则∠A OB=180。，画射线OC，如图2，则∠AOB被分割为两个角LAOC与LBOC. LA OC+∠BOC=∠AOB=1800.像∠AOC与∠BOC这样的两个角互为邻补角．两个角互为邻补角要满足两个条件：（1）有一条公共边（OC为两个角的公共边）；（2）另外一条边互为反向延长线．

还可以通过另外一种方法来理解邻补角，如图3，已知∠AOC，反向延长射线OA．得到射线OB与∠BOC，∠AOC与∠BOC互为邻补角；或者反向延长射线OC，得到射线OD与∠AOD，∠AOC与∠AOD互为邻补角．

2．对顶角，

通过刚才的作图我们得到：一个小于180。的角∠AOC，可以画出它的两个邻补角∠BOC与∠AOD.而且我们知道．∠AOC+∠BOC=∠A OB =180°。，∠AOC+∠AOD=∠COD=180°，根据“同角的补角相等”，可以得到∠BOC=∠AOD.知图4，直线AB与CD相交于点D，我们可以发现∠ BOC与∠AOD不仅大小相等，而且这两个角还有特殊的位置关系：这两个角有公共的顶点，∠BOC的两边分别是∠AOD的两边的反向延长线．像∠BOC与∠A OD这样的两个角，有公共顶点，其中一个角的两边是另外一个角的两边的反向延长线，我们称之为对顶角，图4中还有一对对顶角：∠AOC与∠BOD．在上述探究的过程中，得到对顶角性质：对顶角相等，

在图4中，我们还可以发现，直线AB与CD相交于点O，一个周角被分割成四个小于180。的角：∠AOD，∠AOC，∠BOC，∠BOD．这四个角有公共顶点O，它们有两种位置关系：

（1）有一条公共边，互为邻补角的共有四对角：①∠AOD与∠AOC；②∠AOC与∠BOC;③∠BOD与∠BOC;④∠BOD与∠AOD.（2）無公共边，互为对顶角的共有两对角：①∠AOC与∠BOD；②∠BOC与∠AOD.

在冈5中，∠AOD，∠AOC，∠BOC，∠BOD四个角中，只要有一个角为90。，则这个角的两个邻补角都是90。，根据对顶角相等，这个角的对顶角也是90。，也就是说，这四个角中，只要有一个角是直角，其他的三个角也是直角．当两条直线相交时，形成的四个角中有一个角为900，我们就说这两条直线互相垂直，如图5．

（二）一条直线与两条直线相交形成的八个角之间的关系

一条直线与两条直线相交，或者说两条直线被第三条直线所截，会形成如图6所示的八个角，为了便于表述，我们把直线EF称为截线，把直线AB，CD称为被截线．

1．同位角．

同位角，顾名思义是同样位置的角，同样位置是指两个角都位于截线的同一侧，并且分别在两条被截线的同一侧．观察图6中的∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8.

从图7、图8、图9、图10中我们可以发现互为同位角的两个角组成的图形像字母“F”或者字母“F”旋转、翻折之后的形状．

2．内错角，

两条直线被第三条直线所截形成的八个角中，夹在两条被截线之间（称之为“内”）并且分别在被截线的两侧成交错状（称之为“错”）的两个角为内错角．如图6中的∠3与∠5，∠4与∠6.

我们可以发现互为内错角的两个角组成的图形像字母“Z”或者字母“Z”旋转、翻折之后的形状．

3．同旁内角，

两条直线被第三条直线所截形成的八个角中，夹在两条被截线之间（称之为“内”）并且在被截线的同侧的两个角为同旁内角．如上页图6中的∠3与∠6，∠4与∠5.

我们可以发现互为同旁内角的两个角组成的图形像字母“U”或者字母“U”旋转、翻折之后的形状，

二、认识平行线

平面内不重合的两条直线不相交，我们就说这两条直线平行．如何判定两条直线互相平行呢？

同学们在小学学过利用直尺和三角尺画平行线（如图15）．这种作图法实际上就是把直角三角尺的600的角的顶点从点H处平移到点G处，是通过同位角相等，画出了两条平行线，我们由此得出一个判定两条直线平行的方法：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简单说成：同位角相等，两直线平行．

我们可以思考：内错角、同旁内角是否可以帮助我们判定两条直线平行？

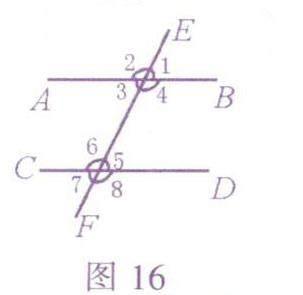
图16中，直线AB，CD被直线EF所截，同位角有四对：∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8．这四对同位角只要有一对相等，根据基本定理，就可以判定直线AB//CD.

图16中内错角有两对：∠3与∠5，∠4与∠6.我们锁定∠3与∠5，猜想：若∠3=∠5，则直线AB与CD平行．若想证明猜想正确，我们应想办法把内错角相等转化到同位角相等上来.∠3有没有同位角？有，∠3的同位角是∠7.∠7与∠5有没有关系？有，∠7与∠5是对顶角．对顶角有何关系？对顶角相等！所以∠7=∠51因为∠3=∠5，所以∠7=∠3，所以AB//CD.

根据上述的探究，我们得到：

两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简单说成：内错角相等，两直线平行．

同学们可以用同样的思路与方法来探究：同旁内角互补，两直线平行．

这就是通过数量关系判定图形的位置关系的应用．反过来，也可以研究两条平行线被第三条直线所截形成的同位角之间的数量关系、内错角之问的数量关系、同旁内角之间的数量关系，进而探索与发现平行线的性质．

试一试

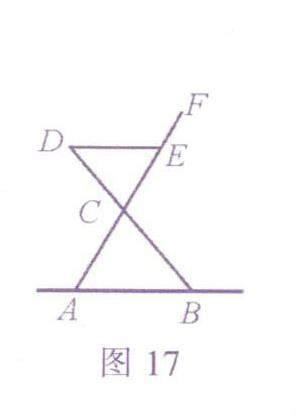
1．（2023年深圳）图17为商场某品牌椅子的侧面示意图．若∠DEF=120°．DE与地面AB平行．∠A BD=500．则∠A CB=（   ）．

A．70°    B.65°C.60°D.50°

2．（2023年大连）如图18，若直线AB//CD， ∠A BE=45°. ∠D=20°．则∠E的大小为（    ）．

A．20°    B.25。

C．30°    D.35°

参考答案：1．A2．B