内凹式闸区波要素计算分析

肖志乔 盛军

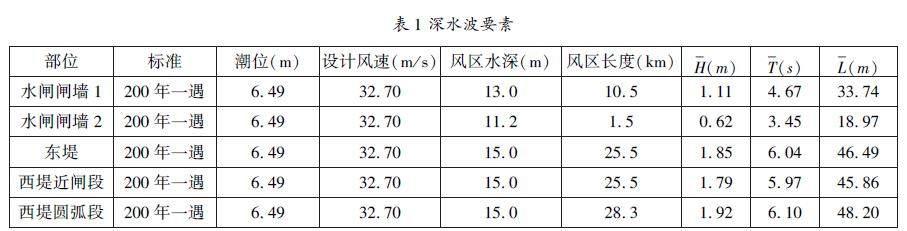
摘 要：相关规范中波浪浅水变形的计算公式适用于岸线顺直、工程前沿滩地平缓的情况，对于岸线曲折多变的内凹式闸区，波要素计算影响因素较多。本文首先采用规范公式进行波要素计算，然后采用国际通用的波浪数值模型进行复核验证。

关键词：内凹式；闸区；波要素；计算

1 概述

设计波要素计算关系到两侧大堤堤顶高程和水闸闸墙顶高程的确定，从而影响整个工程的投资。拟建金汇港南闸闸址前滩地变化明显，所处岸线上下游曲折多变，对波浪传播变形过程存在明显影响。相关规范中浅水变形的计算公式适用于岸线顺直、工程前沿滩地平缓，等深线与岸线平行的情况，与本工程前沿的状况有一定的差距。本文设计波要素首先采用规范公式进行计算，然后采用国际通用的波浪数值模型进行复核验证。

2 规范公式计算成果

2.1 规范公式计算原理

2.1.1 深水波要素计算原理

根据杭州湾水域情况，推算深水波要素。由河海大学、上海市水务局关于《上海风浪实测资料统计分析及风浪谱分析研究》的研究成果表明：上海水域风浪以莆田方法计算的波高、波周期与实测值吻合最好。该公式也是国家《堤防工程设计规范》中所推荐公式，故采用莆田公式：

gH-V2=0.13tanh0.7gdV20.7tanh0.0018gFV20.450.13tanh0.7gdV20.7（1）

gT-V=13.9gH-V20.5（2）

波长计算公式如下：

L=gT-22πtanh2πdL（3）

L0=gT-22π（4）

2.1.2 浅水波要素计算原理

由于波浪传播受地形影响不可忽略，应考虑浅水变形、折射及滩面摩阻作用。波浪变形控制方程及方法：

（1）在周期不变的情况下，波长只与水深有关

L=gT22πtanh（kh）（5）

k=2πL（6）

（2）波速和波群速表达式如下：

C=LT（7）

Cg=nC（8）

n=121+2khsinh（2kh）（9）

（3）折射系数的计算方法如下：

Snell定律表明由波速的变化可确定角度的变化：

sinθ1C1=sinθ2C2（10）

kr=cosθ1cosθ2（11）

（4）浅水系数的计算方法如下：

ks=Cg1Cg2（12）

5）波高的變化即可确定：

H2=H1kskrkf（13）

2.2 规范公式计算成果

鉴于水闸前沿岸线和滩地比较复杂，为了合理确定水闸前沿波要素，本文分别采用《堤防工程设计规范》和《水闸设计规范》中关于风区长度的计算方法计算波要素。其中“水闸闸墙1”工况采用等效风区长度，“水闸闸墙2”工况风区长度依照《水闸设计规范》E.0.1条按水闸前沿水面宽度的5倍（0.3×5=1.5km）取值。

当波浪在浅水区域传播时，受水下地形变化的影响，需作波浪折射、浅水变形计算，其中大堤计算时，需考虑海上运动中心大堤的消浪影响，进行二次浅水变形换算。

2.2.1 深水波要素

2.2.2 浅水波要素及累积率

3 数值模型计算分析

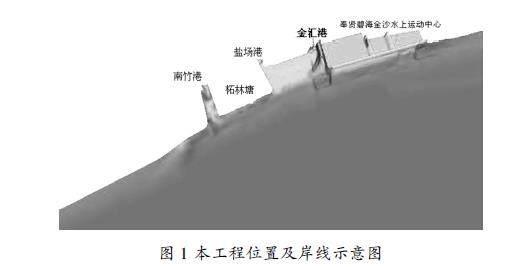
工程位置及岸线见图1。

图1 本工程位置及岸线示意图

3.1 模型概述

采用欧洲丹麦水利研究所DHI开发的MIKE21软件中波谱模型SW进行浅水区波浪数值计算，SW为无结构网格模型，能较为精确和高效地模拟工程中岸线曲折多边和岛屿众多的特殊地形。

3.1.1 计算原理

模型根据波作用守恒原理进行波浪传播变形计算，基本方程如下：

tN+xCxN+yCyN+σCσN+θCθN=sσ（14）

N（σ，θ）=E（σ，θ）/σ（15）

（Cx，Cy）=dx-dt=C→g+U→（16）

Cσ=dσdt=σddt+U-·

x-d-cgk-·U-s（17）

Cθ=dθdt=-1kσddm+k-·U-m（18）

式中E（σ，θ）—能量密度谱，σ—相对频率，θ—波向角。

3.1.2 计算范围及网格

模型由水深约15m等深线处起算，模拟至闸门前位置，考虑到在200年一遇潮位下，金汇港东侧水上运动中心潜堤淹没在水中，即使是正向来波，对波浪传播也可能有影响，潜堤高程分别按5.0m考虑，潜堤和导流坝形状狭长，为准确刻画并模拟其对入射波的影响，建筑物网格最小边长为1.6m。

模型采用无结果网格进行地形数值化，网格边长从外海250m渐变至工程处为1.6m，有限元计算的网格单元104723个，节点52692个，计算面积150km2。

3.2 计算成果

（1）考虑到水闸纵向轴线与正北向偏角为10°，东南侧碧水金沙水上运动中心西侧潜堤长1.0km，结构的高程为5.5～50m左右，对东南向风浪有很好的消减作用，见东南向130°入射时波高等值线云图。

（2）从流场图中可以看出水闸前沿滩地对闸前波浪有一定的消浪效果，东侧海上运动中心大堤消浪效果明显。比较波向入射角度为170°和180°计算方案，由波高分布图可知，由于入射角180°偏西向入射，闸门处波高分布不均匀，闸门东侧波高略大于西侧。入射角170°正向入射时，闸门处波高值基本相同，上述两个计算方案中最大值考虑，闸前波要素取值见表3。

4 计算结果合理性分析

对比规范公式计算结果与数值模型计算结果可知（以闸前波要素为例），水闸闸前波浪要素数值模型计算结果位于规范计算两种结果之间，小于按等效风区长度结果（“水闸闸墙1”工况），大于按5倍闸前水宽计算结果（“水闸闸墙2”工况）。这是因为，水闸虽然位于两侧大堤内，闸前水域相对较为狭窄，但由于水闸距离一线海塘较近（东侧205m，西侧390m），东侧虽有海上运动中心大堤掩护，但高潮位时，只能作为潜坝考虑，且西侧柘林塘以东有一块凹岸水域，杭州湾此处水域宽达90多公里，水闸受波浪袭击作用还是比较大的，故风区长度按《水闸设计规范》中5倍闸前水域宽度（仅1.5km）取值偏小，而按《堤防工程设计规范》中等效风区长度计算难以反映閘前地形变化，结果理应偏大。数值模型计算较好地刻画了地形条件，计算结果比按《堤防工程设计规范》计算值偏小，也属合理，由于两者相差不大，出于安全考虑，本工程波要素取《堤防工程设计规范》计算结果。

结语

本文通过对金汇港南闸的计算分析，认为不同规范计算所得波浪要素不同，数值模型更能反映岸线和地形变化形式，对于岸线曲折复杂的闸区波要素计算按规范计算的同时，应采用数值模型进行复核验证，从工程安全和经济等方面比较后合理选用计算方法。

参考文献：

［1］贺海洪，胡海忠.海堤工程波浪要素计算分析与探讨［J］.人民珠江，2005（3）：4850.

［2］李士峰.堤防工程设计波浪爬高分析与计算［J］.东北水利水电，2006（6）：57+10+71.

［3］苗兴皓，于翠松，王艳玲.水闸波浪要素计算的探讨［J］.山东大学学报（工学版），2002（04）：369371+380.

［4］陈国宁.开敞式海堤波浪计算初探［J］.海峡科学，2007（06）：174176+179.

作者简介：肖志乔（1977— ），男，汉族，湖北汉川人，硕士研究生，高级工程师，研究方向：水利工程。