辩证视角下小学数学“1 与多”的认知路径

叶青

摘要：小学阶段“数的认识”（即对“1”与“多”的辩证认知）是一个对立与统一的过程，其认知内容主要体现为“数量的累加”“位值的拓展”“关系的增减”三个阶段。教师可以结合学生的认知规律与数的认知内容，梳理形成以“1与多”为主题的、历经从绝对性认知到包容性认知再到相对性认知的辩证路径，以促进学生完整建构数的体系。

关键词：1与多；辩证；认知路径；小学数学

一、“1与多”的辩证内涵

数的认识是小学数学教学中非常重要而基础的内容，学生对于数的认识实质上是在建构“1与多”的辩证认知。辩证视角下的“1与多”是一个不断迭代更新的过程，其一，教师要通过大量看得见、摸得着的事物（如1个苹果、1辆汽车、1箱牛奶等）抽象出“1”的本质特征，使学生体会到虽然这些事物的颜色、大小、形状、材质各不相同，但它们都是单个事物，都可以用“1”来表示，进而掌握“1”的概念。在此基础上，学生经历“1”的不断累加，体验到了从数量到数的抽象过程，理解数的大小关系。其二，当1的累加达到一定数量时，学生就产生了位值需求，计数单位应运而生：1个一、1个十、1个百……同样是“1”，当其所在的数位不同时，所表示的数量则会不同。这样，学生对数的认识从借助数量的感性认知逐步走向借助数值的理性认知。其三，数的认识从整数跨越到分数是一次质的飞跃。从数量的理解走向关系的分析，此时“1”的内涵再次被丰富，1个物体、1个计量单位或一些物体都可以看作一个整体（即“单位1”）。在这个过程中，学生对于“1”的理解是站在相对的视角，从原来的量的研究拓展到了关系的研究，经历了量的抽象感悟（即单个与多个关系的抽象感悟——部分与整体）。

数量的“1与多”是具体的、感性的，学生依托数量，从数学的角度认识着数，认知着数值，理解着关系，能深刻感悟到“1”与“多”是不可分离、互相渗透的两个概念：1包含于多，多也包含于1，1与多的辩证关系是物质世界统一性和多样性的体现。

二、辩证视角下“1与多”的认知内容

笔者对于小学数学教材中关于数的认识内容进行梳理，从辩证的视角加以分析，总结为三个阶段。

第一个阶段是数量的累加。教学内容主要出现在一年级认数初期，让学生通过一个一个数数，基于物与数一一对应的过程感受数量的多少，进而抽象成数。这个阶段的学习使学生不断地经历单个量汇聚为多个量，再将具体数量抽象为数的过程，感悟到对于1的包含性，从而积累丰富的感性经验。

第二个阶段是位值的扩展。教学内容主要聚焦于低年段和中年段，其中“10的认识”是一个非常重要的转折点，从10个一到1个十，聚多个量为1个计数单位，打破了之前的认知经验，从“量”走向“计数单位”，是数认识的第一次飞跃。位值的产生为后续更大数的认识奠定了基础，百以内数的认识、万以内数的认识、亿以内数的认识乃至亿以外数的认识都是基于位值展开学习，为一个一个数的复杂路径开辟了一个一个单位计数的简洁路径。

第三个阶段是关系的增减。基于儿童认知发展的特点，从中年段到高年段，关于数的认识逐渐从具体数量的抽象走向了数量关系的推理，“倍的认识”是数认识的第二次飛跃，主要研究的是倍增的关系，为之后研究基于“均分”下的关系认知奠定了基础。“分数的意义”研究的是均分关系，此意义还兼容了量与关系的双重身份，不断丰厚学生对于数的认知，这个阶段的数认识是基于“多对1”的可比性展开的，聚多个部分或多个量为一个整体，从“量”走向“率”。

三、“1与多”的辩证认知路径

结合学生的认知规律与数的研究体系，笔者梳理形成了以下认知路径（见图1）。

（一）初步启蒙：基于具体的量的“1与多”的绝对性认知

对数的研究体系而言，小学阶段的知识结构主要划分为数的意义、数的形式和数的运算三个主要知识模块。初识数是以具体直观的物为认知载体，建立基数与序数的两个基本概念，再衍生出数的顺序、数的大小比较、数的分解与组成。基数表示集合所含元素的个数，学生在学习中经历从现实物体数量的多少到半抽象图形（小棒、小方块、小圆片等）的个数的一一对应，建构“有几个”的数概念，基数的认识是认识自然数的“第一步抽象”。序数则表示某个有序集合中每个元素所占的位置，其本质是反映事物计数的顺序性，通过对“第几个”的思辨，体会到后一个数是前一个数的后继数，以“一”为单位无限制地重复“加一”就能产生任意自然数。此概念的建构则为数的大小比较、数的运算关系等奠定了基础。

教材编排中“0～5的认识”将基数与序数的概念分开教学，而从“6”的认识开始进行了整体教学，学生对于这两个概念的认知经验究竟如何呢？为此，在“6的认识”前，笔者做了相应的评估。教师板书“6”，提出问题：你认识这个数吗？你能找到“6”吗？

生：我的铅笔盒里有6支铅笔；教室的第一排有6张课桌；我在尺子上找到6；从前往后数，我坐在第6个座位上。

师：这些“6”一样吗？为什么？

前测评估情况如下（见表1）。

由此可见，教学前，学生对于事物量的单一性认识具备较为丰富的经验，有68.58%的学生能正确理解①②表示具体的数量，77%的学生能理解④表示顺序。而对于③的争议比较大，可见学生对于此类需要结合特定情境的数意义的理解存在一定的认知混淆，如尺子上从刻度0到刻度6这一段的长度表示6厘米，是基数的内涵；而“6”所对应的这一刻度表示的是第6个1厘米，则是序数的含义。为此，在“0～9的认识”中，教师要通过对现实事物的具体表征让学生在对比辨析中经历由数量到数的形成过程，同时又要理解每一个数分别表示具体的量与相应的顺序的两层意义，明确这两个概念有着本质的区别。

（二）生长思辨：基于计数单位的“1与多”的包容性认知

“10的认识”打破了以“一”作为计数单位的唯一性，在整数的认识中，从10开始，学生逐一认识了百以内数、千以内数、万以内数乃至更大的数，从一个一个数走向10个一是1个十，10个十是1个百……学生逐步体会“1与多”相互包容的关系，进而认识计数单位，发展位值观念，通过相同的数字在不同数位表示不同的意义，经历计数单位不断累加的过程。学生从整数步入小数的认识则反向而行，将“1”不断进行等分，就有了十分之一、百分之一、千分之一的计数单位，经历着计数单位不断细分的过程。这一过程既是数的认识的完整过程，也是数的运算的核心所在。以“小数的意义”一课为例，教师可以如下教学。

一是借助数位顺序表唤醒整数认知。教师在课堂中呈现数位顺序表，介绍整数的相关知识。

师：你们发现了什么？

生：数位、计数单位、数级……

生：有无数个数位就有无数个计数单位。

生：10个十是一百，10个百是一千……10个千万是一亿，每相邻两个计数单位至今的进率是10。

师：从左往右看，100平均分成10份，每份是10；10平均分成10份，每份是1，那么1还能继续分吗？

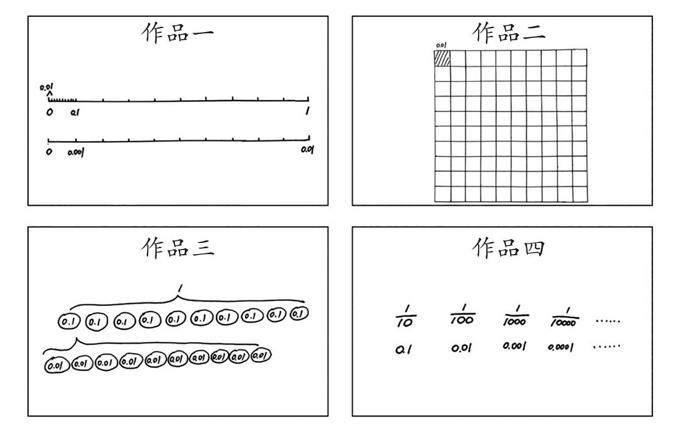
二是尝试多元表征构建小数意义。活动要求：有没有比0.1更小的计数单位？请用喜欢的方式表示。

师：作品四中的省略号表示什么意思？

生：万分之一继续往下分，可以得到更多更小的计数单位。

三是再用数位顺序表使学生感悟计数单位的一致性（见下页图2）。

教师以数位顺序表为载体，引导学生回顾整数的相关知识，着眼不同数位中“1”的满十，衍生出新的计数单位和新的数，初步体会“1”中生“多”，“多”中蕴“1”的辩证关系。教师以此为经验的触发点，引导学生自主表征小数的计数单位，感受细分下得到“多”的变化，从累加到细分丰富了学生对数认识的完整体系，并凸显了计数单位的核心价值。

（三）思维飞跃：基于数量关系的“1与多”的相对性认知

“分数”的意义赋予了数的意义中“量”与“率”的双重内涵，这是学生对于数的认识的又一次飞跃。

该阶段，学生对于数的认知要由理解表征具体“量”的分数走向深化分数对于关系的表达，使思维从理解数量走向分析关系。

例如，在“分数的意义”教学中，根据“直观形象水平—形象抽象水平—本质抽象水平”的概括水平发展结构，教师精选了直观化、半抽象化以及生活化学习素材，通过“关联‘倍再识分数—对立思辨理解分数—对比辨析提炼本质”的学习路径刷新学生对单位“1”的认识，明确其意义的相对性（见表2）。

“分数”基于“率”的意义建构应关联到“倍”，教师通过呈现两组素材的对比，引导学生唤醒已有认知经验进行表达，初步感悟数可以用来表示关系。以“月饼数量是蛋糕数量的2倍”和“蛋糕数量是月饼数量的1/2”的具象表征发现作为标准的“1”的不同，两者之间的结果有时会用整数、有时会用分数表示，使学生初步体会“1”的相对性。这一环节促使学生对于分数的认识从表示具体的量上升至表示两者之间的关系，不断完善“分数”作为数的意義内涵。接着，教师创设“4个蛋糕是6个月饼的几分之几”的认知冲突情境，引导学生体会在单位“1”不变的情况下，平均分的份数不同，则表示的关系也不同，从统一的前提下思考不同的结果，进一步明确分数的意义既要关注谁是单位“1”，还要关注被平均分成了几份，表示了这样的几份。最为关键的一点是对于“1/2个月饼和月饼的1/2”的思辨直击概念本质，让学生豁然开朗，分数的意义可以表达为“量”和“率”，为后续进一步学习有关分数的相应知识做好铺垫。

“1与多”的辩证认知路径旨在将看似遍布各个年级、各个单元的数的认识的内容进行整体架构，实现以主题聚焦散点知识，以阶段式推进实现知识的关联，以辩证的思维视角统整数的体系。

参考文献：

［1］徐文彬，陈韵娴，潘禹辰.小学数学“0～9数的认识”单元知识结构的确立（下）［J］.教学月刊小学版（数学），2023（12）.

［2］张景怡，施慧慧.对立统一辩证思想在小学数学教学中的渗透：以“整体与部分”一课为例［J］.小学数学教师，2022（Z1）.

（责任编辑：杨强）