振动永磁式机械天线的动力学特性研究

张苗 王积硕 宁慧铭 黄楷焱 袁卫锋

摘要：在传统的无线通信领域中，长波通信需要匹配大尺寸信号发射天线，制约了其在中小型平台上的应用。基于逆压电效应、振动理论和麦克斯韦方程组，提出并研制了一种三自由度折返梁结构的振动永磁式机械天线原理样机，建立了电-机械-电磁能理论模型，研究了机械天线的辐射影响因素及其频率调制技术。实验结果表明，通过激发机械天线原理样机的不同振动模态可对电磁波信号进行频率调制，从理论和技术角度为低频段信号的通信提供了新思路。

关键词：机械天线；逆压电效应；多模态；频率调制

中图分类号：O39          文献标志码：A      文章编号：1000-582X（2024）02-119-14

Dynamic characteristics of the mechanical antenna based on vibrating permanent magnet

ZHANG Miao1a，1b， WANG Jishuo1a，1b， NING Huiming2， HUANG Kaiyan3， YUAN Weifeng1a，1b

（1a. School of Manufacturing Science and Engineering; 1b. Key Laboratory of Testing Technology for Manufacturing Process， Ministry of Education， Southwest University of Science and Technology， Mianyang 621010， Sichuan， P. R. China; 2. College of Aerospace Engineering， Chongqing University， Chongqing 400044， P. R. China; 3. School of Mechanical Engineering， Hebei University of Technology， Tianjin 300401， P. R. China）

Abstract： In the traditional field of wireless communication， the application of long-wave communication is constrained on small and medium-sized platforms due to the requirement of large sized signal-transmitting antennas. This paper proposes and develops a three-degree-of-freedom cut-out beam structure of the vibration permanent magnet type mechanical antenna prototype based on the inverse piezoelectric effect， vibration theory， and Maxwells equations. It establishes an electric-mechanical-electromagnetic energy theory model and investigates the radiation influencing factors of the mechanical antenna along with its frequency modulation technique. The experimental results validate that electromagnetic wave signals can be frequency-modulated by exciting different vibration modes of the mechanical antenna prototype. This research offers novel theoretical and technical perspectives for low-band signal communication.

Keywords： mechanical antenna; inverse piezoelectric effect; multi-modal; frequency modulation

低頻电磁波波长较长，具有传播距离远、穿透性强和衰减慢等特点，可广泛应用于水下通信、导航和定位等领域[1?2]。传统天线的尺寸取决于电磁波波长，因此对低频天线而言，天线体积庞大，设备复杂。

目前，根据不同的电磁波激励方式，机械天线可归为3类：驻极体式[3?5]、永磁体式和压电式[6?9]。驻极体式机械天线辐射强度与电荷密度息息相关，但要提高驻极体表面电荷密度较困难。压电式机械天线受限于压电材料尺寸影响，且辐射面积有限。而永磁式机械天线借助于钕铁硼永磁体较高的剩磁[10]，其辐射强度在近场范围内高于另外2种方案。已有大量学者对永磁体式机械天线的频率、相位、幅值和磁场强度等进行了研究[11?12]。Fawole等[13?14]设计了一种增加转子磁体的旋转永磁式机械天线，转子磁体的旋转频率被机电调制。Strachen等[15]提出了一种调制方法，该方法通过改变天线装置周围介质的磁导率，从而改变旋转磁体产生的磁场信号幅值，实现幅值调制。Barani等[16]提出一种新颖的直接倍频和相位调制方案，通过旋转夹在两对正交蝶形高磁导率磁性材料板之间的永磁体，可以调制电磁信号的相位和幅值。在常规单一旋转永磁体天线基础上，Selvin等[17]和Srinivas Prasad等[18?19]提出了磁体阵列便携式机械天线的设计方案，实现了旋转永磁体式机械天线的阵列化，产生更有效的辐射。

由于频率调制受外界噪声影响较小，因此，在机械天线信号调制方面，频率调制是最佳选择。悬臂梁结构简单，模态复杂，可利用悬臂梁结构多模态振动特性与永磁体结合，产生复杂的电磁波。單自由度悬臂梁一阶振动频率与二阶振动频率相差较远，且二阶振动频率振幅响应较小，因此，有研究者设计了折返式和L型的两自由度梁结构，得到了2个接近的谐振频率[20?22]。还有研究者设计的双L型和对称蛇形梁结构可产生多个振动模态[23?24]。受利用压电悬臂梁进行能量采集的启发[25]，提出一种新型振动永磁体式机械天线结构，为三自由度折返梁结构，利用其振动的前三阶固有频率对信号进行频率调制。建立该结构的理论模型，通过实验验证了该模型的正确性；研究振动永磁体的辐射影响因素、通信理论、激励电压优化方法等，并自定义了通信传输协议，实验验证了其可实现地面短距离通信。

1 机械天线原理样机

1.1 机械天线理论基础

机械天线是利用机械运动电荷或磁矩直接激励电磁波的一种新型低频电磁发信天线。基于低频机械天线电磁辐射原理，图1给出了通过机械天线实现通信的技术路线。该路线主要由信号发射端、辐射源和信号接收端组成。在本研究中，辐射源采用高性能钕铁硼永磁体，用于产生强磁场；根据所选调制方式，信号发射端将发射信号对应为辐射源振动状态控制信号，以激发低频电磁波；信号接收端通过线圈对时变磁场进行接收和处理，最终得到辐射源信号并实现通信。

为了提高机械天线辐射效率，同时减小高强度的机械振动，辐射源可以采用多个永磁体，组成磁体阵列天线[17?19]，结合相应振动控制技术，增强磁场强度。为方便进行原理性验证，本研究采用2个永磁体作为辐射源。

1.2 结构设计

由于折返梁前两阶固有频率更接近，能更有效地提高带宽，因此通过研制的一种三自由度折返梁结构来激发电磁波信号。如图2所示，梁1左端完全固定，并把陶瓷压电片（macro-fiber composite， MFC）固定于梁1左端。梁2和梁3向内安装在T型刚性体m1上，以减小装置尺寸，其自由端分别有永磁体2和3（质量块2和3）。利用压电片的逆压电效应，给压电片施加放大后的交变电压，使压电片产生变形，带动梁1振动，永磁体2和3亦随梁2和梁3振动。最终，接收端线圈通过接收永磁体2和3振动产生的叠加磁场实现通信。采用质量-弹簧-阻尼模型[26]，求解该结构的相关参数。

1.3 机械天线的动力学分析

1.3.1 模态分析

为方便分析折返梁结构的振动频率响应，忽略梁和压电片的质量，则三自由度折返梁结构的质量矩阵为

M=[（m_1&0&0@0&m_2&0@0&0&m_3 ）]。    （1）

同样地，根据材料力学中标准刚度影响系数法获得结构的刚度矩阵为

K=[（k_11&k_12&k_13@k_21&k_22&k_23@k_31&k_32&k_33 ）]，  （2）

其中，

{（k_11=（（B_2 C_1-B_1 C_2）（B_3+B_1）D-（B_3 C_1-B_1 C_3）（B_1+B_2）D）/（（A_2 B_1-A_1 B_2）（B_3 C_1-B_1 C_3）-（A_3 B_1-A_1 B_3）（B_2 C_1-B_1 C_2）），@k_12=（B_1 D（B_3 C_1-B_1 C_3））/（（A_2 B_1-A_1 B_2）（B_3 C_1-B_1 C_3）-（A_3 B_1-A_1 B_3）（B_2 C_1-B_1 C_2）），@k_13=（B_1 D（B_1 C_2-B_2 C_1））/（（A_2 B_1-A_1 B_2）（B_3 C_1-B_1 C_3）-（A_3 B_1-A_1 B_3）（B_2 C_1-B_1 C_2）），@k_21=（-（A_1 C_2-A_2 C_1）（A_1+A_3）D+（A_1 C_3-A_3 C_1）（A_1+A_2）D）/（（A_1 C_3-A_3 C_1）（A_2 B_1-A_1 B_2）-（A_1 C_2-A_2 C_1）（A_3 B_1-A_1 B_3）），@k_22=（（A_3 C_1-A_1 C_3）A_1 D）/（（A_1 C_3-A_3 C_1）（A_2 B_1-A_1 B_2）-（A_1 C_2-A_2 C_1）（A_3 B_1-A_1 B_3）），@k_23=（（A_1 C_2-A_2 C_1）A_1 D）/（（A_1 C_3-A_3 C_1）（A_2 B_1-A_1 B_2）-（A_1 C_2-A_2 C_1）（A_3 B_1-A_1 B_3）），@k_31=（（A_2 B_1-A_1 B_2）（A_1+A_3）D+（A_1 B_3-A_3 B_1）（A_1+A_2）D）/（（A_1 B_3-A_3 B_1）（A_2 C_1-A_1 C_2）-（A_1 B_2-A_2 B_1）（A_3 C_1-A_1 C_3）），@k_32=（（A_3 B_1-A_1 B_3）A_1 D）/（（A_1 B_3-A_3 B_1）（A_2 C_1-A_1 C_2）-（A_1 B_2-A_2 B_1）（A_3 C_1-A_1 C_3）），@k_33=（（A_1 B_2-A_2 B_1）A_1 D）/（（A_1 B_3-A_3 B_1）（A_2 C_1-A_1 C_2）-（A_1 B_2-A_2 B_1）（A_3 C_1-A_1 C_3）），）┤  （3）

（A_1=2E_2 I_2 E_3 I_3 L_1^3  ，&B_1=E_2 I_2 E_3 I_3 （2L_1^3-3L_1^2 L_2） ，@C_1=E_2 I_2 E_3 I_3 （2L_1^3-3L_1^2 L_3） ，&A_2=-2E_2 I_2 E_3 I_3 L_1^2 L_2  ，@B_2=E_3 I_3 （2E_1 I_1 L_2^3+6E_2 I_2 L_1 L_2^2-2E_2 I_2 L_1^2 L_2） ，&C_2=2E_2 I_2 E_3 I_3 （3L_1 L_2 L_3-L_1^2 L_2） ，@A_3=-2E_2 I_2 E_3 I_3 L_1^2 L_3  ，&B_3=2E_2 I_2 E_3 I_3 （3L_1 L_2 L_3-L_1^2 L_3） ，@C_3=E_2 I_2 （2E_1 I_1 L_3^3+6E_3 I_3 L_1 L_3^2-2E_3 I_3 L_1^2 L_3） ，&D=6E_1 I_1 E_2 I_2 E_3 I_3  ，）    （4）

式中：E_1、E_2和E_3是梁1、2和3的弹性模量；I_1、I_2和I_3是梁1、2和3的转动惯量；L_1、L_2和L_3是梁1、2和3的长度。折返梁结构中各部件的参数列于表1中。通过求解三自由度系统方程Ku=ω^2 Mu的特征值和特征向量u来获得其固有频率及振型。

表2为前三阶振型向量，得出前三阶固有频率理论值分别为f1=11.5 Hz，f2=12.6 Hz和f3=22.0 Hz。从表2中可以得出：一阶振型中，永磁体2和3的振幅相同且明显大于质量块1；二阶振型中，质量块1的振幅几乎为零，永磁体2和3的振幅相等，相位相差180°；三阶振型中，永磁体2和3的振幅相同且小于质量块1的振幅。

1.3.2 振动位移

结合公式（1）和（2）可得到三自由度折返梁结构的振动运动方程为

{（m_1 y ¨_1+c_11 y ˙_1+c_12 y ˙_2+c_13 y ˙_3+k_11 y_1+k_12 y_2+k_13 y_3=F（t） ，@m_2 y ¨_2+c_21 y ˙_1+c_22 y ˙_2+c_23 y ˙_3+k_21 y_1+k_22 y_2+k_23 y_3=0 ，@m_3 y ¨_3+c_31 y ˙_1+c_32 y ˙_2+c_33 y ˙_3+k_31 y_1+k_32 y_2+k_33 y_3=0 ，）┤ （5）

式中：y_1、y_2和y_3分别是质量块1、永磁体2和3在垂直方向的位移；c_ij和k_ij分别表示阻尼矩阵和刚度矩阵中的相关分量；F（t）表示梁1根部压电片产生的激励。

在实际分析中，要精确地确定阻尼矩阵是非常困难的，通常将阻尼矩阵简化为质量和刚度矩阵的线性组合，表示为

C=αM+βK，     （6）

式中，α、β分别是质量阻尼系数和刚度阻尼系数。取阻尼比ξ=0.001，根据α=4πξf_1 f_2/（f_1+f_2）和β= ξ/[π（f_1+f_2）]可以确定质量阻尼系数和刚度阻尼系数α、β的值。

1.3.3 压电片对梁结构的作用力

压电片在外部交流电压u（t）的激励下，产生的应变为

ε=Δl/l=（u（t））/h_p ?d_31，    （7）

u（t）=A_i sin（2πf_i t），    （8）

式中：Δl為压电片变形量；l为压电片的长度；u（t）为功率放大器输出到压电片的交变电压；h_p为压电片的厚度；压电片的压电常数取d_31=-2.1×〖10〗^（-10）  C/N[27]；f为激励电压的频率。压电片产生的应变作用在梁上，使得梁产生弯矩

M=（εE_1 I_1）/（0.5h_1 ）。    （9）

该弯矩可等效为作用在梁1右端的集中力F（t）。根据图3（a），可得出压电片产生的应变对梁产生的非线性振动位移x_1和线性振动位移x_2，以及转角θ的表达式如下

（x_1=（Ml^2）/（2E_1 I_1 ）  ，&    x_2=θ（L_1-l） ，&     θ=Ml/（E_1 I_1 ）） 。 （10）

根据图3（b），可得出作用在梁1右端的集中力F（t）产生的位移

x=（F（t）L_1^3）/（3E_1 I_1 ） 。    （11）

因此，建立弯矩和集中力对梁产生的位移相等的关系式

（Ml（2L_1-l））/（2E_1 I_1 ）=（F（t）L_1^3）/（3E_1 I_1 ）。   （12）

进一步化简，可求出等效集中力F（t），

F（t）=（3Ml（2L_1-l））/（2L_1^3 ）。  （13）

1.4 数值计算和结果

四阶龙格-库塔方法（Runge-Kutta methods）计算精度高，数据准确，因此采用此方法对方程组（5）进行数值求解。计算中每一步计算步长为0.005，压电片激励信号的频率为三自由度折返梁结构的前三阶固有频率，依次为11.5、12.6、22.0 Hz时，对应的激励时间分别为0～40 s、40～80 s和80～120 s。结构中使用的参数如表3所示，求解出质量块1、永磁体2和3的位移。

质量块1、永磁体2和3的位移y_1、y_2和y_3如图4所示。由图4（a）～（c）可知，质量块1、永磁体2和3在前三阶固有频率下的位移与振型（见表2）一致。

2 永磁体和线圈的磁场通信理论

2.1 振动永磁体产生的磁场

永磁体作为辐射源，本研究将对其振动状态下产生的磁场强度进行理论研究。如图5（a）所示，对于空间中任意一点P（a， b），其磁感应强度B可表示为

B=（μ_0 m）/2π cosθ（jk/r^2 +1/r^3 ）e^（-jkr） a_r+（μ_0 m）/4π sinθ（-k^2/r+jk/r^2 +1/r^3 ）e^（-jkr） a_θ，      （14）

式中：μ_0为真空磁导率；k为波数，k=2π/λ，λ为波长；m为磁偶极矩；r为永磁体到P点的距离；a_r、a_θ和a_φ分别为r、θ和φ方向的单位矢量，如图5（a）所示。

由于电磁波波长较长，约为107 m，波数k≈6×〖10〗^（-7） m-1，远远小于1。因此，在近场范围内，包含k/r^2和k/r的项忽略不计，包含1/r^3的项起主要作用，磁场强度与r^3呈反比关系。在实际应用中仅需考虑电磁波的近场即可，电磁波的磁场强度可简化为

B=（μ_0 m）/（2πr^3 ） cosθa_r+（μ_0 m）/（4πr^3 ） sinθa_θ。   （15）

近场处任意一点的磁场强度可表示为B=√（B_r^2+B_θ^2 ）。若永磁体沿y轴做简谐运动，且其振动位移定义为y（t），如图5（b）所示，磁场的幅值为

B=（μ_0 m√（4[b-y〖（t）]〗^2+a^2 ））/（4π{[b-y〖（t）]〗^2+a^2 }^2 ） 。   （16）

由式（16）可知，振动永磁体产生的磁场强度与永磁体振动位移有关。

在本研究中，低频电磁波的接收装置为线圈，位于y轴。设线圈截面积为Ac，接收线圈的匝数为Nc，则通过线圈的磁通量ψ=BA_c。根据法拉第电磁感应定律，若线圈处于发射天线的时变磁场中，则线圈会产生同频率的感应电动势，可得感应电动势与磁场强度之间的关系

U=-N_c  dψ/dt=-N_c A_c  dB/dt 。 （17）

2.2 信号处理

本研究中对采集到的感应电动势信号采用Superlets（SLs）[28]方法进行处理，其原理是建立一个具有固定中心频率的小波集，且具有一系列不同的周期，其处理方法与小波变换类似，该方法的优点是可同时兼顾高时间和高频率分辨率。在文献[28]中，定义了一个改进的Morlet（亦称为Gabor）函数：

ψ_（f_g，c） （t）=1/（B_c √2π） e^（- t^2/（2B_c^2 ）） e^（j2πf_g t） ，  （18）

B_c=c/（k_sd f_g ） 。     （19）

式中：f_g为小波的中心频率；c为母小波的周期数；B_c为时间扩展参数，控制小波的时间方差；设置k_sd=5。

SLs被定义为中心频率为f_g且具有一系列不同周期数的小波

SL_（f_g，o）={ψ_（f_g，c） ├|c=c_1，┤ c_2，...，c_o } 。   （20）

式中：o为SLs的阶数；c1， c2， …， co表示小波集中每个小波的周期数。当o=1时，表示一阶SL即为具有c1个周期数的单個小波。

SLs对信号x的响应定义为小波集中各个小波对x信号响应的几何平均（关于几何平均的具体解释见文献[28]的补充材料）

R[SL_（f_g，o）]=√（o&∏_0^o?〖R[φ_（f_g，c_i ）]〗） 。 （21）

式中，R[φ_（f_g，c_i ）]是小波i对信号x的响应，即两者之间的卷积

R[ψ_（f_g，c_i ）]=√2?x*ψ_（f_g，c_i ） ，      （22）

式中，*是复卷积算子。

需要指出的是：1）式（22）并不是信号的实际强度，经过SLs处理后，仅能恢复信号实际强度的一半；2）SLs变换的计算方法与CWT类似，仅是利用SLs代替了小波，因此，一阶的SL变换即为CWT。

2.3 通信理论

对于振动式机械天线而言，可以通过控制永磁体振动频率来实现电磁波的频率调制。制定的传输协议如表4所示，规定三自由度折返梁的前三阶振动频率f_1、f_2和f_3分别代表“1”码、“2”码和“3”码。信号的时域长度T1=10 s、T2=15 s和t2=5 s，分别代表“1”码和“2”码，t2时刻无激励信号，表示1个信息码结束，1个信息码包含3组频率-时间的组合。

设激励电压的幅值A_1=A_2=A_3=200 V，将1.4节中求解出的y_2和y_3带入公式（17），可得出由于永磁体振动产生的时变磁场引起的感应电动势。在传递信息时，激励信号的频率和时域长度如表5所示，规定每40 s为1个信息码，总共4个信息码。按照表4的传输协议转换成信息码[‘112132，‘211231，‘123121，‘312211]进行传输，线圈接收到振动永磁体2和3产生的理论感应电动势如图6（a）所示，可以看出有4个明显的周期信号。

基于SLs信号分析方法对接收端线圈接收到的信号进行处理，可得到信号的时频信息，如图6（b）所示。根据图6（b）中信号频率的大小和信号的时域长度，可得出4组与发送端相同的信息码，理论验证了通过机械天线实现低频电磁波通信的可行性。

2.4 接收信号等强度下的激励电压

在本研究中，为方便接收端对接收到的信号进行解码处理，需保证接收信号的强度一致，此小节研究了激励电压和接收端的信号强度之间的关系。图6（b）中，颜色的深浅代表了信号强度的大小。可以看出，二阶和三阶频率的信号的强度明显小于一阶，在实际通信过程中，二阶和三阶频率信号可能会被视为噪声，这不利于接收端对接收到的信号进行解码处理。根据1.3节中，激励电压决定永磁体振动位移的大小，又由2.1节可知，接收端的感应电动势的强度与永磁体振动位移有关，因此，根据公式（5）和（17）可确定接收端感应电动势强度和激励电压的关系，具体流程图见图7。

计算过程中，取一阶激励频率f_1对应的激励电压幅值A_1=200 V，对应信号强度P_1=1.2×〖10〗^（-4），根据图7的流程，得到A_2=525 V，A_3=612 V，信号强度如图8（a）所示，从图中可以看出，当机械天线结构振动稳定后，频率为f_1、f_2和f_3的信号强度相同，约为P=1.2×〖10〗^（-4）。再按照表5传输信号，接收端线圈接收到的感应电动势如图8（b）所示，也就是原始信号，从图中可以看出，时间和频率信息并不能清晰直接得到，因此需要对其进行进一步处理。将接收到的感应电动势采用SLs信号处理，得到信号时频图，如图8（c）所示，与图6（b）相比， f_1、 f_2和f_3对应的信号的颜色深浅一致，说明了信号强度相同，利用优化后的激励电压值进行通信，更有利于接收端对接收信息进行解码。

3 实验研究

本小节首先通过研制的机械天线原理样机验证振动理论的正确性，然后验证原理样机在低频范围内通信的可行性和有效性。

3.1 模型验证

根据1.2节中的理论模型，研制机械天线原理样机如图9（b）所示，主要由梁1、梁2、梁3、压电片、钕铁硼永磁体和T型块组成。折返梁结构中梁1由铝板制成，梁2和梁3由碳素工具钢制成，具有d_31压电效应的MFC片材（M-8557-P1）安装在梁1根部。实验装置示意图如图9（a）所示，激励信号由函数发生器产生，经过功率放大器放大处理后，最后馈送至压电片，压电片产生变形，带动折返梁结构振动，产生的电磁波经线圈接收后，传输至示波器。

在本研究中，为实现编码式通信，设定具有明显频率-时间特征的激励信号作为验证对象。在实验过程中，函数发生器改变激励信号的频率，可得折返梁的振动状态。可得折返梁的前三阶固有振动频率，分别为f_1=11.6 Hz、 f_2=12.5 Hz和f_3=22.0 Hz，前三阶频率值与理论值基本相同。相应的振动状态如图10所示，图10（a）～（c）分别为折返梁前三阶固有频率对应的振动状态。相比于图10（b）和图10（c），图10（a）中永磁体2和3的振幅明显最大，并且是同相位振动。另外，从图10（b）中可以看出，永磁體2和3振动的相位发生明显变化，大致相差180°。从图10（c）中可以看出，永磁体2和3同相位振动。与表2对比可知，实验所得前三阶固有频率振动规律与理论完全吻合，验证了1.2节所建立理论模型的正确性。

3.2 通信实验

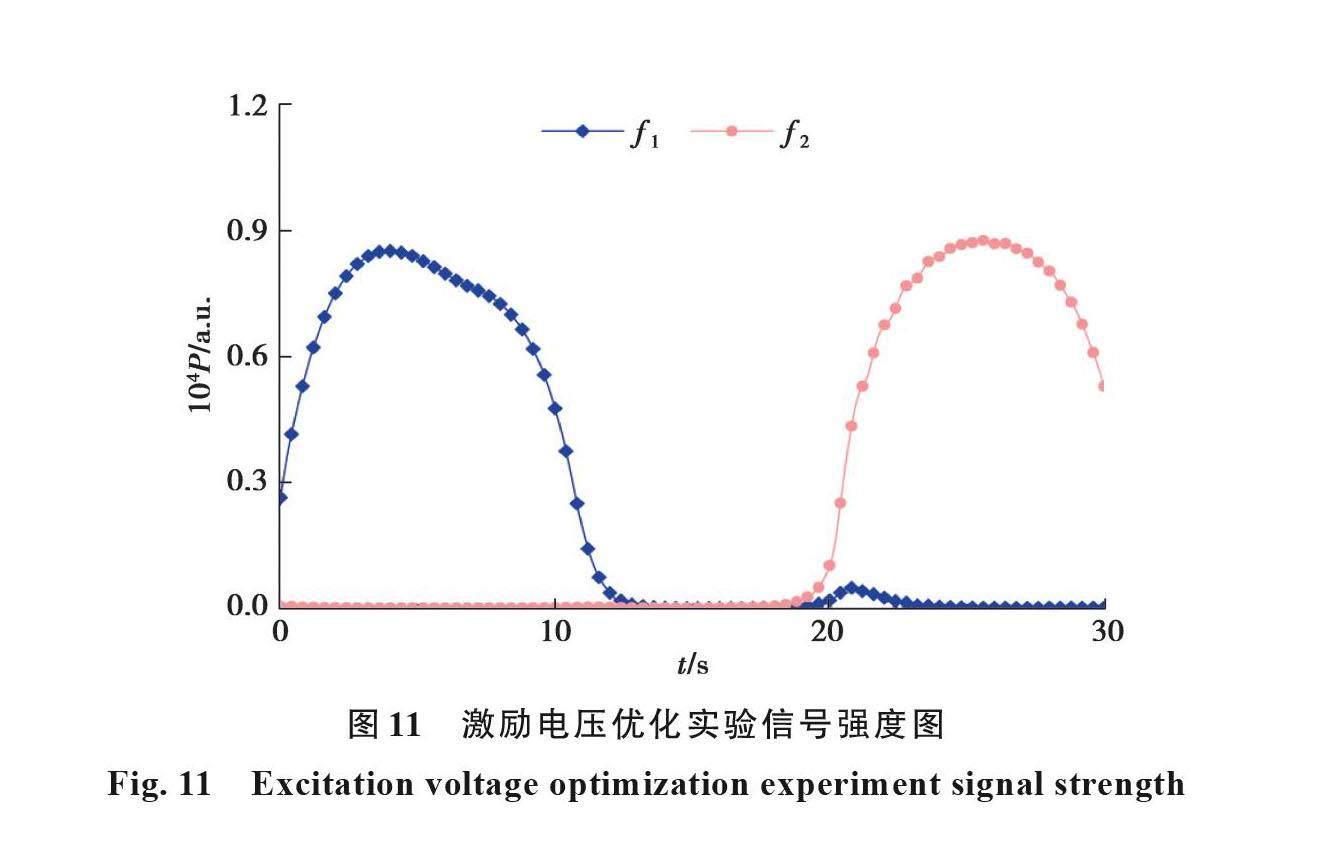
实验装置如图9，由1.3节求出的结构第三阶模态可知，此时梁1的振动位移较大，梁1的材料为铝，在振动过程中易变形失效，故在实验时，不采用三阶频率。f1对应的激励电压幅值为A1=200 V，f2对应的激励电压幅值为A2=525 V，数据处理结果如图11所示。图11中，P1=P2=0.9×10-4，说明信号的强度相同。

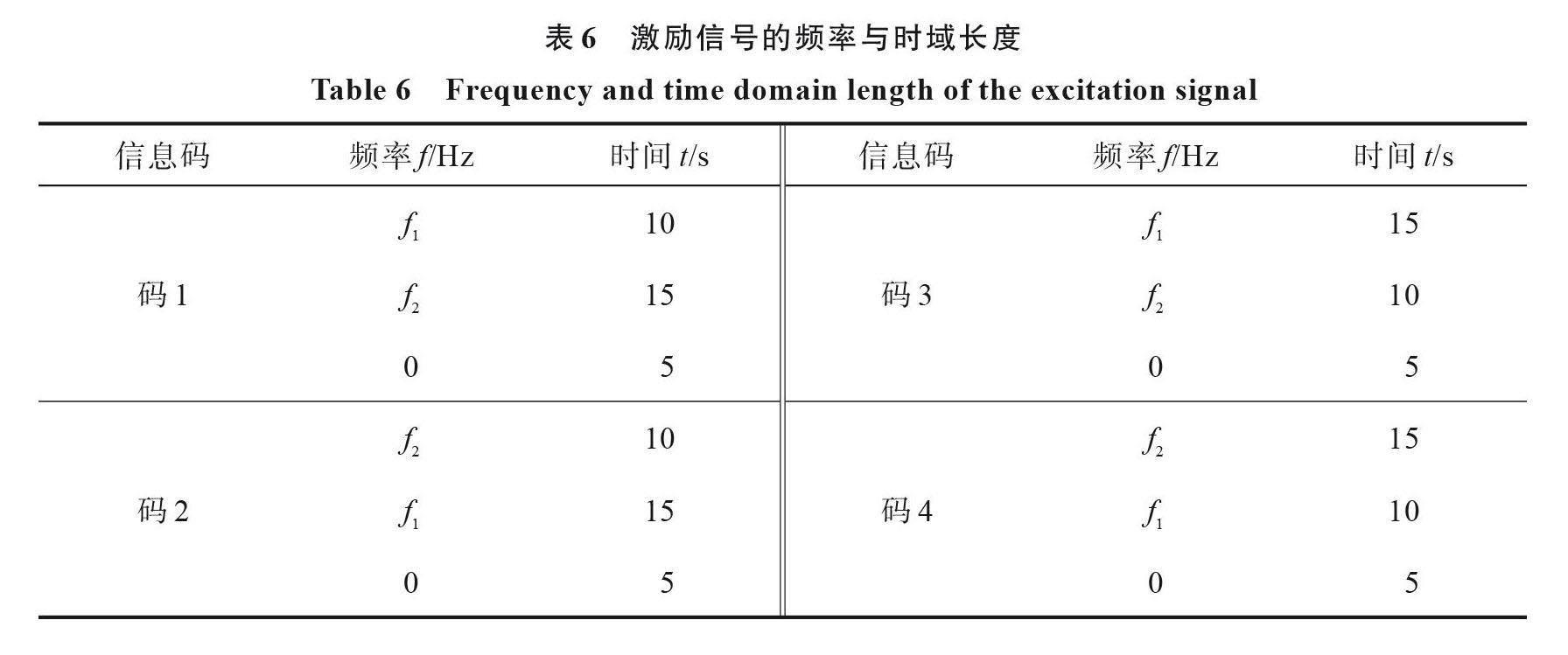
按照优化后的激励电压幅值进行通信实验，利用线圈对信号进行接收。线圈置于图9（a）中所示位置，其轴线垂直于水平面，线圈与永磁体之间的垂直距离为H=5 cm。基于此，线圈可对悬臂梁2和3自由端永磁体振动产生的时变磁场进行感应，以产生感应电动势。在实验时，如图9（b）所示为实验装置示意图，激励信号的频率与时域长度均列于表6中，信号采样频率fs=125 Hz。根据表4机械天线传输协议，将发射端的频率-时间信息转换成码[‘1122，‘2112，‘1221，‘2211]进行传输，同样采用SLs信号分析方法对接收信号进行处理。

图12（a）为接收信号的原始信息，与图6（a）相比，信号的幅值大致相同。图12（b）为接收信号的时频信息，从图中可以看出该信号的频率成份有2种，分别为11.6 Hz和12.5 Hz。另外，还可得出接收信号编码特征有所不同且与激励信号的信息码[‘1122，‘2112，‘1221，‘2211]相一致。根据表4的传输协议，接收端可以解码出与激励信号相同的4个信息码。而且与图6（b）不同的是，每个频率的信号强度大致相同，将幅值乘以对应的频率值f_1和f_2，得到图12（c），从中也可以解码出与发射端相同的信息码。这种解码方式有利于接收端处理信号，可提高通信效果。

值得一提的是，从图12（b）中，可以看出，2个信号之间是不连续的，此不连续是在实验过程中刻意设计的，目的是为了减少2个频率切换时，折返梁系统振动时，因惯性造成的前一个频率信号拖延对接收端处理数据的影响。在一个信息码2组频率对应的信号之间设置间隔，可以使接收端更加清晰地识别信息码。另外，机械天线的优势在于其可依靠小尺寸结构产生低频电磁波，由于极低频电磁波波长较长，所以衰减慢，传播距离远。但是，根据基本的电磁通讯原理可知，频率越低，通信效率也越低。例如，本研究实验中，若1个信息码中包含2段不同频率的信号，此2种信号持续时间分别为T1和T2，1个信息码中不同频率间的间隔为t1=10 s，不同信息码之间的间隔为t2，则数据传输速率可以通过公式2/（T1+T2+t1+t2）计算，单位是bit/s。

综上所述，提出了一种三自由度折返梁结构的机械天线原理样机，求解出了折返梁结构的前三阶固有频率（f_1、 f_2和f_3）、固有振型和振动位移；实验验证了三自由度折返梁结构的前三阶固有频率和固有振型与理论研究的一致性；按照制定的通信传输协议，将激励信号的频率（f_1、 f_2和f_3）和时域长度进行编码通信，对接收到的信号进行解码，在理论上实现了通信。通过对SLs信号处理的研究，得出了激励电压幅值与信号强度的关系，使得接收端不同频率的信号强度相同。实验结果表明接收信号与激励信号的时频信息具有高度一致性，验证了该机械天线原理样机实现低频信号通信的可行性和有效性。

本研究的重点是探索机械天线的机理，因此采用的永磁体磁性和质量仅满足原理验证所需，信号发射功率低。同时，信号采集装置为1个普通小线圈（截面积和匝数均小），线圈中产生的感应电动势不高。所以，天线通信距离短，0.5 m之外信号即非常微弱。振动永磁体产生的磁场强度与永磁体的剩磁和永磁体的体积有关，例如：增加永磁体数量，并采用剩磁更强的永磁体，可以大幅度提高通讯距离。由于波长较长，信号衍射能力和穿透性好，小重量的机械天线可用于复杂环境中群体机器人之间的通信。另外，本研究中研制的机械天线也可用于水下通信，其可行性已通过实验验证，但鉴于篇幅原因未在本文中列出。

4 结  论

提出了一种新型振动永磁式机械天线。通过研制的机械天线原理样机实验验证了其通信的可行性。可得结论如下：

1）基于逆压电效应、振动永磁式机械天线辐射理论和低频电磁波通信原理，提出了一种三自由度折返梁结构的机械天线原理样机理论模型，得出折返梁结构的前三阶固有频率和振动永磁体磁场强度的关系式；

2）利用永磁体振动位移和接收端感应电动势之间的关系，得出了不同频率激励信号的激励电压之间的关系；

3）通过激发自主研制的机械天线原理样机的不同振动模态对电磁波信号进行了频率调制，对激励信号的频率和信号时域长度进行编码，验证了该原理样机实现通信的可行性。

总之，将逆压电效应、电磁学和振动力学相结合，实现了利用小尺寸机械天线对低频段信号的激发，提供了一种机械天线装置设计的新思路。

参考文献

［1］  Liu Y， Gong S H， Liu Q， et al. A mechanical transmitter for undersea magnetic induction communication[J]. IEEE Transactions on Antennas and Propagation， 2021， 69（10）： 6391-6400.

［2］  崔勇， 吴明， 宋晓， 等. 小型低频发射天线的研究进展[J]. 物理学报， 2020， 69（20）： 171-183.

Cui Y， Wu M， Song X， et al. Research progress of small low-frequency transmitting antenna[J]. Acta Physica Sinica， 2020， 69（20）： 171-183. （in Chinese）

［3］  Barani N， Sarabandi K. Mechanical antennas： emerging solution for very-low frequency （VLF） communication[C]//2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting. July 8-13， 2018， Boston， MA， USA. IEEE， 2019： 95-96.

［4］  Liang B W， Cui Y， Song X A， et al. Multi-block electret-based mechanical antenna model for low frequency communication[J]. International Journal of Modeling， Simulation， and Scientific Computing， 2019， 10（5）： 1950036.

［5］  Bickford J A， McNabb R S， Ward P A， et al. Low frequency mechanical antennas： electrically short transmitters from mechanically-actuated dielectrics[C]//2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting. July 9-14， 2017， San Diego， CA， USA. IEEE， 2017： 1475-1476.

［6］  Kemp M A， Franzi M， Haase A， et al. A high Q piezoelectric resonator as a portable VLF transmitter[J]. Nature Communications， 2019， 10： 1715.

［7］  Hassanien A E， Breen M， Li M H， et al. Acoustically driven electromagnetic radiating elements[J]. Scientific Reports， 2020， 10： 17006.

［8］  Dong C Z， He Y F， Li M H， et al. A portable very low frequency （VLF） communication system based on acoustically actuated magnetoelectric antennas[J]. IEEE Antennas and Wireless Propagation Letters， 2020， 19（3）： 398-402.

［9］  Chen H H， Liang X F， Dong C Z， et al. Ultra-compact mechanical antennas[J]. Applied Physics Letters， 2020， 117（17）： 170501.

［10］  Sugimoto S. Current status and recent topics of rare-earth permanent magnets[J]. Journal of Physics D： Applied Physics， 2011， 44（6）： 064001.

［11］  王曉煜， 张雯厚， 周鑫， 等. 旋转磁偶极子式超低频发射天线辐射特性[J]. 兵工学报， 2020， 41（10）： 2055-2062.

Wang X Y， Zhang W H， Zhou X， et al. Radiation characteristics of rotating magnetic dipole super-low frequency transmitting antenna[J]. Acta Armamentarii， 2020， 41（10）： 2055-2062. （in Chinese）

［12］  周強， 施伟， 刘斌， 等. 旋转永磁式机械天线的研究与实现[J]. 国防科技大学学报， 2020， 42（3）： 128-136.

Zhou Q， Shi W， Liu B， et al. Research and practice of the mechanical antennas based on rotating permanent magnet[J]. Journal of National University of Defense Technology， 2020， 42（3）： 128-136. （in Chinese）

［13］  Fawole O C， Tabib-Azar M. An electromechanically modulated permanent magnet antenna for wireless communication in harsh electromagnetic environments[J]. IEEE Transactions on Antennas and Propagation， 2017， 65（12）： 6927-6936.

［14］  Fawole O C， Tabib-Azar M. Electromechanically-modulated permanent magnet antennas for wireless communication[C]//2017 IEEE Sensors. October 29-November 1， 2017， Glasgow， UK. IEEE， 2017： 1-3.

［15］  Strachen N， Booske J， Behdad N. A mechanically based magneto-inductive transmitter with electrically modulated reluctance[J]. PLoS One， 2018， 13（6）： e0199934.

［16］  Barani N， Kashanianfard M， Sarabandi K. A mechanical antenna with frequency multiplication and phase modulation capability[J]. IEEE Transactions on Antennas and Propagation， 2021， 69（7）： 3726-3739.

［17］  Selvin S， Srinivas Prasad M N， Huang Y K， et al. Spinning magnet antenna for VLF transmitting[C]//2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting. July 9-14， 2017， San Diego， CA， USA. IEEE， 2017： 1477-1478.

［18］  Srinivas Prasad M N， Selvin S， Tok R U， et al. Directly modulated spinning magnet arrays for ULF communications[C]//2018 IEEE Radio and Wireless Symposium （RWS）. January 15-18， 2018， Anaheim， CA， USA. IEEE， 2018： 171-173.

［19］  Srinivas Prasad M N， Tok R U， Fereidoony F， et al. Magnetic pendulum arrays for efficient ULF transmission[J]. Scientific Reports， 2019， 9： 13220.

［20］  Wu H， Tang L H， Yang Y W， et al. A novel two-degrees-of-freedom piezoelectric energy harvester[J]. Journal of Intelligent Material Systems and Structures， 2013， 24（3）： 357-368.

［21］  Wu H， Tang L H， Yang Y W， et al. Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester[J]. Journal of Intelligent Material Systems and Structures， 2014， 25（14）： 1875-1889.

［22］  Yao M H， Liu P F， Ma L， et al. Experimental study on broadband bistable energy harvester with L-shaped piezoelectric cantilever beam[J]. Acta Mechanica Sinica， 2020， 36（3）： 557-577.

［23］  Huang S F， Dong G B， Zhou M Y. Low-frequency broadband piezoelectric vibration energy harvester based on double L-shaped beam structures[J]. Journal of Vibration Engineering & Technologies， 2022， 10（8）： 3179-3189.

［24］  He L F， Narita F. Design and optimization of a multimode low-frequency piezoelectric energy harvester[J]. International Journal of Applied Mechanics， 2022， 14（4）： 1-15.

［25］  赵兴强， 温志渝. 柔性梁颤振机理在压电式微型风能收集器设计中的应用[J]. 重庆大学学报， 2013， 36（8）： 145-150.

Zhao X Q， Wen Z Y. Design of a miniaturized wind energy harvester based on a fluttering flexible beam[J]. Journal of Chongqing University， 2013， 36（8）： 145-150. （in Chinese）

［26］  任泽民， 凌霄霄， 乔金丽， 等. 多自由度结构动力方程解析解的改进算法[J]. 河北工业大学学报， 2018， 47（4）： 68-74.

Ren Z M， Ling X X， Qiao J L， et al. Improved analytical algorithm of dynamic formula of a multipledegree-of-freedom system[J]. Journal of Hebei University of Technology， 2018， 47（4）： 68-74. （in Chinese）

［27］  Meng X D， Lin S Y. Analysis on coupled vibration of piezoelectric ceramic stack with two piezoelectric ceramic elements[J]. The Journal of the Acoustical Society of America， 2019， 146（4）： 2170-2178.

［28］  Moca V V， B?rzan H， Nagy-D?b?can A， et al. Time-frequency super-resolution with superlets[J]. Nature Communications， 2021， 12： 337.

（編辑  郑洁）