数字钻孔图像岩体结构面自动化识别方法

张占旭 苏俊辉 吕光祖 骆维斌 许存禄

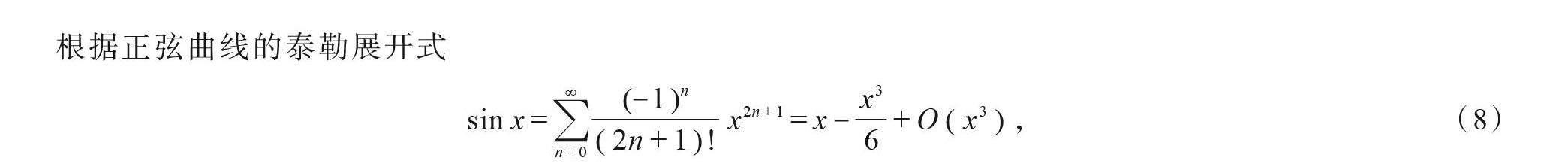
摘要：数字钻孔摄像技术能准确获取钻孔中岩体结构面特征信息，针对现有数字钻孔图像分析人力需求量大、主观性强、计算量大的不足，研究提出方案实现数字钻孔摄像技术采集的钻孔内壁图像自动识别。首先，用二维伽马函数光照自适应矫算法对图像进行光照均匀处理，利用经过预训练的DexiNed网络对矫正后图像边缘进行特征提取；其次，提出Epremoval方法处理边缘点噪声提取感兴趣区域；最后，根据正弦曲线泰勒展开式对图像中的表征数据进行多项式拟合。通过对得到曲线进行计算、空间变换和数理变换得到岩体结构面参数。以某隧道工程的数字钻孔图像为例，研究提出的算法结果优于人工辅助判读结果。

关键词：数字钻孔图像；岩体结构面；感兴趣区域；泰勒展开式；多项式拟合

中图分类号：TU45          文献标志码：A      文章编号：1000-582X（2024）02-040-11

Automatic identification of rock structure surface based on digital borehole images

ZHANG Zhanxyu1， SU Junhui 1， LYU Guangzu2， LUO Weibin1， XU Cunlu2

（1. Gansu Road and Bridge Construction Group Co.， Ltd.， Lanzhou 730000， P. R. China; 2. School of Information Science and Engineering， Lanzhou University， Lanzhou 730000， P. R. China）

Abstract： Digital borehole camera technology can accurately acquire information regarding the structural surface characteristics of rock within a borehole. To address the shortcomings such as labor-intensity， subjectivity， and computational intensity associated with existing digital borehole image analysis， this paper introduces a new analysis scheme to automate the recognition of borehole interior images captured by digital borehole camera technology. The proposed scheme begins by uniformly illuminating images using a two-dimensional gamma function light-adaptive correction algorithm. Next， edge features are extracted using a pre-trained DexiNed network. To tackle edge point noise and extract the region of interest， the Epremoval method is employed. Finally， the method performs polynomial fitting on the characterization data in the image utilizing the Taylor expansion of the sine curve. The parameters of the rock structure surface are obtained by calculation， spatial transformation and mathematical transformation of the obtained curves. The algorithm is applied to the digital borehole image of a tunnel project as an illustrative example. The obtained results are compared with the results of manual assisted interpretation， revealing superior recognition capabilities of the proposed method.

Keywords： digital drilling images; rock discontinuities; area of interest; Taylor expansion; polynomial fitting

巖体中结构面的分布和组合特征决定了岩体的工程地质、力学性质，是各种岩体地质工程问题的重要控制因素，岩体结构面信息是进行岩体结构分析和岩体稳定性评价的基础[1]。岩体结构面信息的识别主要研究如何提取岩体内部岩体结构面的粗糙度、张开度等几何特征[2]，是岩体结构面重要研究方向，也是工程地质和岩石工程领域的热点问题[3]。

岩体结构面几何参数获取现有方法包括接触式测量和非接触式测量。接触式测量方法主要使用测线法和测窗法等[4]，需要人工利用皮尺和罗盘等传统测量工具在现场结构面上进行人工测量，现场测量危险性高、效率低，结果精确度受人为因素影响[5?6]。非接触式测量技术包括数字近距离摄影测量、无人机低空摄影和三维激光扫描技术等。其中，数字近距离摄影测量是以数字存储形式从图像中识别和提取物理信息的方法[7]，是便捷高效获取岩体结构面几何参数的有效技术方法[8]。

利用数字近距离摄影测量技术测量得到数字钻孔图像的后续处理是岩体特性分析的关键[9]，目前主要是人工判读法和自动识别[10]。人工辅助判读因个体差异，在计算岩体结构面正弦曲线参数时存在一定误差，导致效率低且难快速精准识别、提取参数[11]。随着计算机视觉技术的飞速发展，利用图像处理算法自动识别岩体结构面成为高效技术手段。国内外学者在探索岩体结构面的自动识别技术方面进行了大量研究，汪进超等[12]结合钻孔图像中岩体结构面的性质，采用自适应中值滤波法对钻孔图像进行去噪处理，提出结合梯度算子与最大类间方差法，对分割后的图像进行Canny算子边缘检测，最后使用多项式曲线拟合获得结构面的正弦曲线。袁浩琪等[13]根据图像特征确定面积半径并采用同心圆展开法得到矩形展开图，利用SIFT特征点完成与Ransac算法的精确匹配，并采用加权平均法完成图像融合。宋琨[14]等提出一种考虑结构面图像灰度分布特点的智能识别方法，通过对图像进行灰度化、降噪等预处理操作，根据特征值获取特征图像，并进行边缘检测、阈值分割及形态学处理，对边缘曲线进行拟合实现结构面特征的智能化识别。Zou等[15]提取图像中的结构面剖面线、分析倾角，将结构面圆形剖面线转换为三维特征进行分析。Hough变换或与其他技术结合使用是最常用的方法[16-19]，Hough变换对岩体结构面拟合，获取特征参数，提高岩体结构面检测精度和效率。尽管Hough变换方法在结构面图像分析方面取得较好效果，但其应用也面临着对图像噪声、光照变化和曲线形状的敏感性，以及计算复杂度较高等问题限制。夏丁等[19]对钻孔图像进行中值滤波处理、高通增强、拉普拉斯锐化、二次中值滤波处理、灰度均衡和Canny二值化等预处理操作，使用二次Hough变换识别结构面的正弦曲线。随着深度学习进一步发展，基于深度神经网络方法被应用在岩体结构面识别，取得良好效果。苏钰桐等[20]选取煤矿井下钻孔图像在VOC2007上制作数据集并采用Darknet-53网络进行训练[21]，实现对钻孔图像裂隙的快速准确识别，但深度神经网络的模型训练需要较大人力物力收集数据和细致标注[22]。首先，利用图像去噪和增强方法对图像进行预处理，然后，分割图像，对抽取的纹理或边缘特征进行分析，在岩体结构面几何特征提取和检测方面取得进展，但在结构面错综复杂且数量多、结构面图像受到噪声污染、及成像现场光照强度不均匀等情况，图像预处理流程过于复杂，且预处理效果不理想，导致最终结构面自动识别性能较差，无法满足在工程环境中的应用[23]。

研究提出了一种新的数字钻孔图像岩体结构面自动化识别方法——DET（DexiNed-epremoval-talor）。为应对光照强度不均匀问题，DET首先用二维伽马函数光照自适应矫正算法对图像进行处理；为避免深度神经网络的模型训练需要大量数据和精细标注的问题，DET利用在BIPED数据集上训练好的DexiNed[24]（dense extreme inception network for edge detection）网络对矫正后数字钻孔图像进行边缘提取。随后，通过Epremoval方法对提取后的图像进行处理，该方法能在尽可能保留岩体结构面正弦曲线特征的同时去除大部分边缘点。最后，DET对经过预处理的数字钻孔图像提取感兴趣区域（region of interest，ROI）并根据正弦曲线的泰勒展开式，对表征数据进行多项式拟合，得到的曲线计算出正弦曲线的特征参数。笔者对得到的特征参数进行数理变换、空间变换得到岩体结构面的几何信息估计值。

1 数字钻孔图像感兴趣区域的提取

为减少因图像采集时光照不均的问题，DET使用二维伽马函数光照自适应矫算法。为降低算法复杂度，加强对特征区域的提取，DET使用经过预训练的DexiNed网络对数字钻孔图像进行边缘特征提取[24]， 提出Epermoval方法，能有效去除边缘点噪声的同时最大限度保留岩体结构面的特征。根据数字钻孔图像岩体结构面呈分段分布的特性，设计特征信号CS（characteristic signals），实现对ROI的提取。

1.1 基于DexiNed网络的预处理

工程实践中采集的数字钻孔图像存在大量噪声，不利于对岩体结构面特征的识别。按照图1中的流程对数字钻孔图像进行预处理，减少噪声对岩体结构面表征的影响，增强感兴趣区域的特征。图2为各预处理流程效果图。

1.1.1 光照矫正

研究使用光照自适应校正算法的具体实现过程如图3所示，方法采用双边滤波法提取非均匀光照图像的光照分量，根据光照分量分布特性对二维伽马函数进行自适应调节，在保持原始图像中有效信息的同时对非均匀光照图像进行矫正。该方法既能提高图像视觉效果，又能挖掘出更多黑暗区域的细节[25]。如图2（b）和图4所示，该方法使光照更均匀，有效减少因光照问题造成的误差。

1.1.2 DexiNed网络处理

DexiNed可看作是密集端初始网络（Dexi）和上采样块（UB）2个子网络，其模型结构如图5所示，当Dexi输入RGB图像时，UB提供来自Dexi每个块的特征映射，避免深层中遗漏边缘。在不需要任何预先训练数据情况下，DexiNed可获得较好效果。如图2（c）所示，数字钻孔图像经过DexiNed网络处理，得到较为清晰的特征图，但仍包含一些噪声。

1.1.3 Epremoval方法

为有效去除边缘点噪声的同时最大限度保留岩体结构面特征，笔者提出Epremoval方法。该方法分为去除小面积边缘点噪声和去除大面积边缘点噪声。首先，寻找图像中的边缘点轮廓信息，计算每个轮廓围成的图像面积，得到数组S_e [i]（i=0，1，…，N_e-1），其中N_e表示检测出的边缘点个数；其次，设置去除小面积边缘点噪声的阈值T_e；最后，将S_e [i]小于T_e的邊缘点对应I_b （x，y）中所有（x，y）设置为背景色。具体公式如下所示

I_b （x，y）={（0           ，if  S_e [i]≤T_e，@I_b （x，y） ，otherwise，）┤    （1）

式（1）中：S_e [i]（x，y）表示边缘点S_e [i]对应图像I_b （x，y）中所有（x，y）。经过上述操作，仍存在一些面积较大位于中间的边缘点噪声，对图像进行遍历，计算每行的表征数据DH_b （i）

DH_b （i）=∑_（j=0）^（w-1）?〖E（i，j）〗 ，   （2）

式（2）中：w表示图像的宽度。计算不同区域DH_b （i）≠0的连续行数并存储到数组L_e [i]（i=0，1，…，N_e-1）中，得到max（L_e [i]）。令ψ=max（L_e [i]），对I_b （x，y）中（i，i+h-ψ-1） 行进行遍历，在第i行的图像左边缘形成一个ψ×w?3的矩阵E，右边缘形成一个矩阵S，对矩阵E和S中图像的像素点进行计算，直到遍历结束，得到图像I_t （x，y），计算公式为

I_t （i）={（I_b （i）  ，if   ∑_（i=0）^（w/3-1）?〖sgn（∑_（j=0）^（ψ-1）?〖E（i，j）+∑_（j=0）^（ψ-1）?〖S（i，j）〗〗）〗≠0，@0       ，otherwise，）┤ （3）

式中：sgn是一类符号函数，具体应用如下

sgn（number）={（-1   ，       （number<0），@0    ，      （number=0），@1    ，       （number>0），）┤       （4）

经过Epremoval方法处理，效果图如2（d）所示，去除大量噪声值，保留岩体结构面的正弦特征。

1.2 感兴趣区域的提取

数字钻孔图像经过预处理后效果如图2（d）所示，图像中感兴趣区域的特征明显。笔者采用的感兴趣区域特征信号提取公式如下所示

CS（i）=1/w ∑_（j=0）^（w-1）?〖（I_b （i，j）-1/N ∑_（i=0）^（h-1）?∑_（j=0）^（w-1）?〖I_b （i，j）〗）〗 ， （5）

式中，h表示图像的高度。如图6所示，计算出的特征信号CS（i）能较好表示感兴趣区域的范围，通过特征信号边界完成对感兴趣区域的提取。

2 岩体结构面特征参数

在识别过程中，因交错结构面相互干扰，结构面破碎是导致未呈现正弦特性的原因，研究仅识别呈现固定单周期特性的单一岩体结构面。在处理岩体结构面的正弦函数曲线时，函数曲线公式可以表示为

y=A?sin（ω?x+φ）+K，     （6）

式中：A为幅度；ω为角速度；K为基线；φ为初始相位。

2.1 线性拟合

如图6所示，数字钻孔图像被划分出多个感兴趣区域。对感兴趣区域中的兴趣点进行分析，曲线y_ta的计算公式为

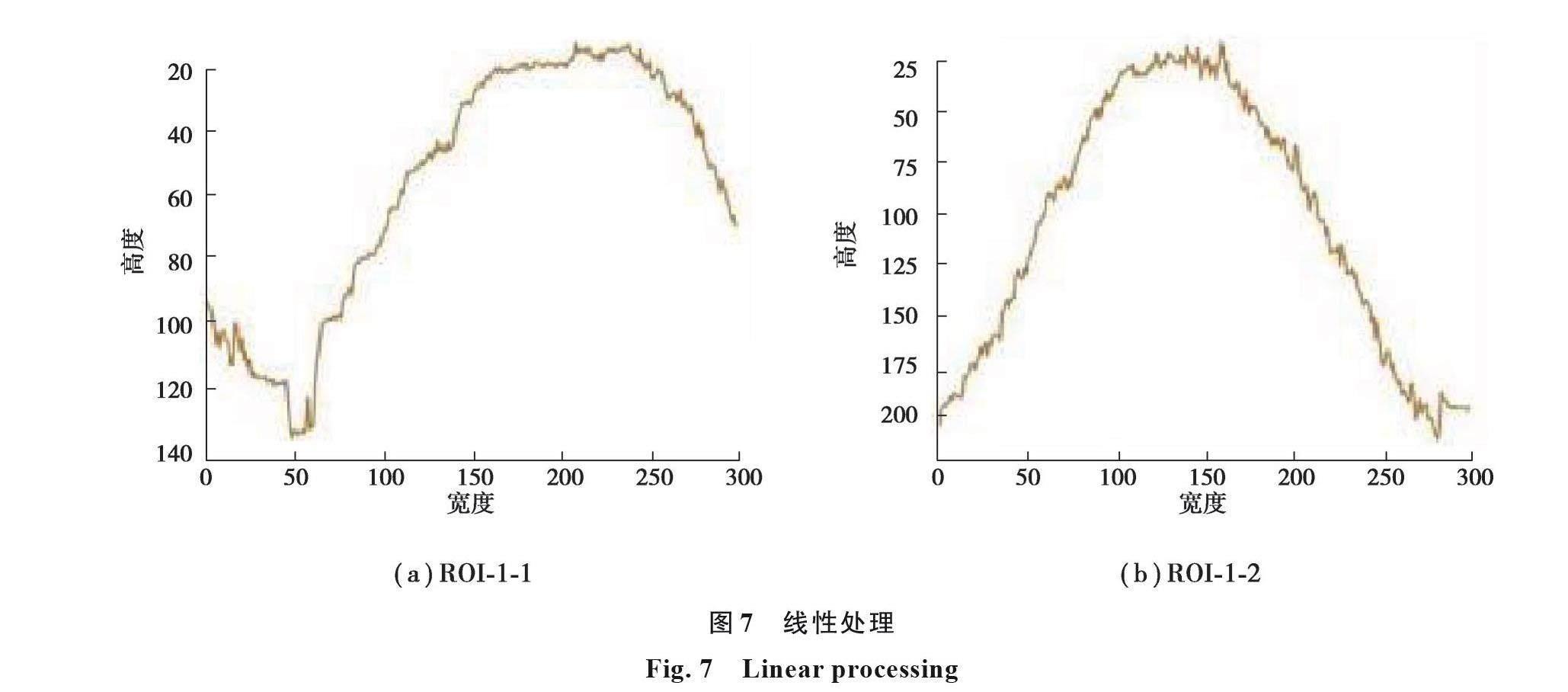
y_ta （i）={（1/h_ta  ∑_（j=0）^（h_ta）?〖I_ta （i，j）                    ，if    I_ta （i，j）≠0，〗@?_ta y_ta （i-1）+?_ta y_ta （i+n）    ，otherwise，）┤   （7）

式中：I_ta代表提取出的感兴趣区域的图像；h_ta表示I_ta的高；?_tal和?_tar代表y_ta （i-1）和y_ta （i+n）结合时的权重，y_ta （i+n）代表y_ta （i）后第一个不为0的点。经过上述处理得到曲线y_ta，如图7所示，该方法将感兴趣区域中的兴趣点分布较好表示出来，尽可能保留岩体结构面的正弦特征。

根据正弦曲线的泰勒展开式

sinx=∑_（n=0）^∞?〖（-1）〗^n/（（2n+1）！） x^（2n+1）=x-x^3/6+Ο（x^3） ，   （8）

将正弦曲线近似3次多項式，对y_ta多项式线性拟合，如图8所示，观察到拟合效果良好，得到的多项式曲线y_l根据极点数目分为2种情况。即多项式曲线y_l包括一个极点情况，即y_l^ （i）=0（?！i）和多项式曲线y_l包括2个及以上极点数目情况，即y_l^ （i）=0（i_1，i_2，…，i_n∈i，n≥2），这2种情况计算正弦曲线角速度ω、基线K和幅度A是不同的。

2.1.1 确定正弦曲线的角速度

多项式曲线y_l的角速度ω的计算公式

ω={（π/|i_n-i_（n+1） |     ，if     y_l^ （i）=0（i_1，i_2，…，i_n∈i，n≥2），@π/w             ，if     y_l^ （i）=0（?！i），）┤   （9）

式中，y_l^ （i）表示y_l在i处的导数。

2.1.2 确定正弦曲线的基线位置

根据正弦曲线的性质可知计算正弦曲线基线K的公式为

K={（（y_l [j]+y_l [j+π/ω]）/2    ，if     0≤j≤π/ω（y_l^ （i）=0（i_1，i_2，…，i_n∈i，n≥2）），@ y_l 〖[j]〗_min                  ，if     0≤j≤w （y_l^ （i）=0（?！i）），）┤ （10）

式中，y_l^ （i）=0（i_1，i_2，…，i_n∈i，n≥2）情况下，采取一种类似于投票机制方法，将计算的K值保存，得到其中众数和最终基线位置[26]。

2.1.3 确定正弦曲线的幅度

根据正弦曲线的性质可知计算位置参数幅度A的公式为

A={（〖y_l〗_min+K        ，if   y_l^ （i）=0（i_1，i_2，…，i_n∈i，n≥2），@〖y_l〗_max- 〖y_l〗_min    ，if   y_l^ （i）=0（?！i）。）┤   （11）

2.1.4 确定正弦曲线的相位

任选y_l曲线中的一点（x_use，y_use），根据式（5）可得φ计算公式为

φ=arcsin（（y_use-K）/A）-ωx_use 。    （12）

2.2 岩体结构面特征参数的计算

实验计算出数字钻孔图像感兴趣区域的正弦参数后，通过数理变换、空间变换得到岩体结构面的空间参数。设二维图像中的坐标为（x_img，y_img），真实三维坐标为（x_real，y_real，z_real），钻孔半径为R，图像宽度为W，像素坐标转换为空间坐标的转换公式如下所示[15]

{（x_real=R?cos（2π x_img/W），@y_real=R?sin（2π x_img/W），@z_real=S?y_img 。）┤    （13）

岩体结构面空间平面单位法向量NV的转换公式如下所示

{（NV_x=（A?S?sin（φ））/√（R^2+A^2 S^2 ），@NV_y=（A?S?cos（φ））/√（R^2+A^2 S^2 ）@NV_z=R/√（R^2+A^2 S^2 ） 。）┤ ，   （14）

式（13）（14）中S的计算公式为

S=S_real/S_img  ， （15）

式（15）中：S_real代表实际距离，S_img代表图像距离。得到岩体结构面的单位法向量后，通过数理转换得到倾向α和倾角β，公式如下所示

{（a={（arctan（（NV_y）/（NV_x ））                 ，if      NV_x≥0_，NV_y≥0，@arctan（（NV_y）/（NV_x ））+180      ，if      NV_x<0，@arctan（（NV_（y@））/（NV_x ））+360      ，if      NV_x≥0_，NV_y<0，）┤@b=|arctan（√（NV_x^2+NV_y^2 ）/（NV_z ））|。）┤    （16）

3 实例应用

研究使用来自某隧道工程的数字钻孔图像，如图9所示，钻孔直径为90 mm，比例尺S=2.885 1。图9（a）的钻孔完整性一般，钻孔内壁中间存在竖直方向干扰源，造成原因是存在竖直大裂缝、过度曝光或者黄色干扰源，识别难度较大；图9（b）和图9（c）的钻孔完整性较好，但中间存在横条噪声。

利用提出的一系列算法，对图9进行DexiNed网络处理，提取其边缘特征，使用Epremoval方法减少边缘点噪声，如图10所示。对ROI进行提取，如图11所示，可较好提取出每个巖体结构面，共提取出6个ROI。最后，对图像中的表征数据进行多项式拟合，对每个ROI中的图像进行处理，如图12所示，得到其多项式拟合曲线。

通过拟合的曲线计算得到相应正弦曲线参数，数理变换和空间变换获得倾向、倾角等参数，如表1所示，发现偏差较小，大部分岩体结构面取得了良好效果。其中，对于识别得到的Img1-ROI2感兴趣区域，2条岩体结构面裂缝相距太近且中间存在竖直干扰源将2条裂缝交叉在一起；Img1-ROI1的结果偏差较大，如图9（a）所示，感兴趣区域的正弦特征不够明显，且受中间竖直干扰源影响较大。

4 结 论

研究对数字钻孔图像中岩体结构面的自动识别展开研究。主要结论如下：

1）在数字钻孔图像实际采集过程中，由于光照变化、阴影及物体表面反射特性差异，造成成像场景光照不均匀。利用二维伽马函数光照自适应矫正算法对图像进行处理，采用双边滤波方法提取非均匀光照图像的光照分量，根据光照分量分布特性对二维伽马函数进行自适应调节，保持原始图像有效信息，实现对图像亮度的自适应校正处理得到增强图像。

2）使用神经网络对数字钻孔图像进行预处理并提出Epremoval方法处理边缘噪声。使用经过预训练的DexiNed网络对数字钻孔图像进行边缘特征提取。DexiNed提取边缘后，提出Epremoval方法对边缘点噪声进行处理，取得较好效果。该方法极大简化数字钻孔图像的预处理步骤，同时获得更好效果和广泛应用，不仅在保留岩体结构面表征的同时显著减少噪声，便于获取岩体结构面的特征数据。通过设计简单特征信号，能对图像中感兴趣的区域进行有效分割，使后续详细识别的部分被分割出来，降低计算量。

3）研究没有使用传统Hough变换方法对图像正弦特征参数进行提取，而是借鉴正弦函数泰勒展开式，对图像进行多项式拟合得到光滑曲线，计算岩体结构面的正弦参数，对岩体结构面的特征参数进行空间和数理变换，得到图像几何信息。该过程显著降低了计算需求，更加快速识别岩体结构面，准确率高。

参考文献

［1］  Lan H X， Zhang Y X， Macciotta R， et al. The role of discontinuities in the susceptibility， development， and runout of rock avalanches： a review[J]. Landslides， 2022， 19（6）： 1391-1404.

［2］  Ge Y F， Cao B， Tang H M. Rock discontinuities identification from 3D point clouds using artificial neural network[J]. Rock Mechanics and Rock Engineering， 2022， 55（3）： 1705-1720.

［3］  葛云峰， 夏丁， 唐輝明， 等. 基于三维激光扫描技术的岩体结构面智能识别与信息提取[J]. 岩石力学与工程学报， 2017， 36（12）： 3050-3061.

Ge Y F， Xia D， Tang H M， et al. Intelligent identification and extraction of geometric properties of rock discontinuities based on terrestrial laser scanning[J]. Chinese Journal of Rock Mechanics and Engineering， 2017， 36（12）： 3050-3061.（in Chinese）

［4］  赵萌， 唐辉明， 詹红兵， 等. 求解岩体裂隙产状三维概率分布的数值方法[J]. 地球科学， 2022， 47（4）： 1470-1482.

Zhao M， Tang H M， Zhan H B， et al. A numerical method for solving three-dimensional probability distribution of rockmass fracture orientations[J]. Earth Science， 2022， 47（4）： 1470-1482.（in Chinese）

［5］  Lv H T， Bao H， Lan H X， et al. Detection method of buried depth of single crack in rock mass based on thermal infrared response[J]. Journal of Earth Sciences and Environment， 2022， 44（06）： 1048-1065.

［6］  宣程强， 章杨松， 徐文涛. 基于数字表面模型的岩体结构面产状获取[J]. 水文地质工程地质， 2022， 49（1）： 75-83.

Xuan C Q， Zhang Y S， Xv W T. Extraction of the discontinuity orientation from a digital surface model[J]. Hydrogeology & Engineering Geology， 2022， 49（1）： 75-83. （in Chinese）

［7］  Wu F Q， Wu J， Bao H， et al. Rapid intelligent evaluation method and technology for determining engineering rock mass quality[J]. Rock Mechanics Bulletin， 2023， 2（2）： 100038.

［8］  Xu X H， Bao H， Lan H X， et al. Sampling interval-size effects and differential sensitivities of different morphology parameters of rock joint[J]. Journal of Structural Geology， 2022， 155： 104530.

［8］  ZouX J， SongH， WangC. A high-precision digital panoramic borehole camera system for the precise analysis of in situ rock structures[J]. Rock Mechanics and Rock Engineering， 2021， 54（11）： 5945-5952.

［10］  MohanArun P S. Crack detection using image processing： a critical review and analysis[J]. Alexandria Engineering Journal， 2018， 57（2）： 787-798.

［11］  黃达， 钟助. 基于单个钻孔孔壁电视图像确定地下岩体结构面产状的普适数学方法[J]. 地球科学， 2015， 40（6）： 1101-1106.

Huang D， Zhong Z. A universal mathematical method for determining occurrence of underground rock discontinuity based on TV picture of wall of a single borehole[J]. Earth Science， 2015， 40（6）：1101-1106. （in Chinese）

［12］  汪进超， 王川婴， 胡胜， 等. 孔壁钻孔图像的结构面参数提取方法研究[J]. 岩土力学， 2017， 38（10）： 3074-3080.

Wang J C， Wang C Y， Hu S， et al. A new method for extraction of parameters of structural surface in borehole images[J]. Rock and Soil Mechanics， 2017，38（10）：3074-3080. （in Chinese）

［13］  Yuan H Q， Xu F X， Fu P L. Research on the processing algorithm of drilling image[C]//Eighth International Conference on Electronic Technology and Information Science （ICETIS 2023）. May 24-26， 2023. Dalian， China： SPIE， 2023.

［14］  宋琨， 孙驰， 安冬， 等。数字钻孔全景影像中结构面特征智能识别方法[J]. 地质科技通报， 2020， 39（5）： 17-22.

Song K， Sun C， An D， et al. Intelligent identification method for rock discontinuities properties by digtial borehole panoramic images[J]. Bulletin of Geological Science and Technology， 2020， 39（5）： 17-22. （in Chinese）

［15］  Zou X J， Wang C Y， Wang Y T， et al. Morphological feature description method of structural surface in borehole image during in-situ iInstrumentation[J]. Rock Mechanics and Rock Engineering， 2020， 53： 2947-2956.

［16］  Zhao K， Han Q， Zhang C B， et al. Deep hough transform for semantic line detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2021， 44（9）： 4793-4806.

［17］  Vijayarajeswari R， Parthasarathy P， Vivekanandan S， et al. Classification of mammogram for early detection of breast cancer using SVM classifier and Hough transform[J]. Measurement， 2019， 146： 800-805.

［18］  Wang J， Fu P， Gao R X. Machine vision intelligence for product defect inspection based on deep learning and Hough transform[J]. Journal of Manufacturing Systems， 2019， 51： 52-60.

［19］  夏丁， 葛云峰， 唐辉明， 等. 数字钻孔图像感兴趣区域分割与岩体结构面特征识别[J]. 地球科学， 2020， 45（11）： 4207-4217.

Xia D， Ge Y F， Tang H M， et al. Segmentation of interest region of digital drilling image and recognition of rock mass structural surface features[J]. Journal of Earth Science， 2020， 45（11）： 42074217. （in Chinese）

［20］  苏钰桐， 杨炜毅， 李俊霖. 基于YOLO v3的煤岩钻孔图像裂隙智能识别方法[J]. 煤矿安全， 2021， 52（4）：156-161.

Su Y T， Yang W Y， Li J L. Intelligent fracture identification method for coal rock borehole images based on YOLO v3[J]. Coal Mine Safety， 2021， 52（4）： 156-161. （in Chinese）

［21］  Redmon J ， Farhadi A .YOLOv3： an incremental Improvement[EB/OL].（2018-04-08）[2021-11-20]. https：//arxiv.org/abs/1804.02767..

［22］  Corbane C， Syrris V， Sabo F， et al. Convolutional neural networks for global human settlements mapping from Sentinel-2 satellite imagery[J]. Neural Computing and Applications， 2021， 33： 6697-6720.

［23］  張梦原， 陈俊智. 基于数字图像处理的岩体结构面迹线检测[J]. 化工矿物与加工， 2023， 52（1）： 29-33.

Zhang M Y， Chen J Z. Rock mass discontinuity trace detection based on digtial image processing[J]. Industrial Minerals & Processing， 2023， 52（1）： 29-33. （in Chinese）

［24］  Xavier S， Edgar R， Angel S. Dense rxtreme inception network： towards a robust CNN model for edge detection[J]. 2020 IEEE Winter Conference on Applications of Computer Vision （WACV）， 2020：1912-1921.

［25］  刘志成， 王殿伟， 刘颖， 等. 基于二维伽马函数的光照不均匀图像自适应校正算法[J]. 北京理工大学学报， 2016， 36（2）： 191-196.

Liu Z C， Wang D W， Liu Y， et al. Adaptive correction algorithm for illumination in homogeneous images based on two-dimensional gamma function[J]. Journal of Beijing Institute of Technology， 2016， 36（2）： 191-196. （in Chinese）

［26］  邹长春， 史謌. 一类正弦曲线的Hough变换快速检测方法[J]. 计算机工程与应用， 2002（4）： 1-3.

Zou C C， Shi G. A fast detection method for the Hough transform of a class of sinusoidal curves[J]. Computer Engineering and Applications， 2002（4）： 1-3. （in Chinese）

（编辑  侯湘）