非零方阵的一类加法分解

崔 建

(安徽师范大学 数学与统计学院,安徽 芜湖 241002)

0 引 言

线性代数是高等院校理工经管类和部分文史类的专业基础课,而矩阵是线性代数中最基本也是最核心的概念,其理论贯穿于线性代数始终.因此,对矩阵理论的深入理解是学好线性代数课程的重要因素.下面介绍几类特殊的矩阵.

称方阵A是可逆的,如果存在方阵B使得AB=In;称矩阵N是幂零的,如果存在正整数m使得Nm=O;称矩阵E是幂等的,如果E2=E[1].可逆阵、幂零阵、幂等阵在矩阵理论研究中发挥重要作用.基于上述几类特殊方阵,学者们研究了方阵的加法分解性质,如文献[2]证明了任意方阵均可表示为两个可逆阵的和;由文献[3]可知,任意方阵都可写成一个可逆阵与一个幂等阵之和.2016年,环论学者Calugareanu与Lam在文献[4]中引入fine环的概念(即环中任意非零元素均能表示为一个幂零元与一个可逆元之和).受此启发,本文从线性代数的角度研究非零方阵的加法分解,证明了任意非零方阵均可表示为一个幂零阵与一个可逆阵之和,推广了文献[3]中的相关结论,同时把这一结果应用到线性空间中线性变换的分解中.

1 相关引理

为简化主要结论的证明,本节给出如下几个引理.

引理1可逆阵可分解为一个幂零阵与一个可逆阵之和.

证设A是可逆阵,则A=O+A为一个幂零阵与一个可逆阵之和,结论得证.

引理2非零幂零阵可分解为一个幂零阵与一个可逆阵之和.

证设N是非零幂零矩阵.由文献[5]可知,N相似于一个Jordan形矩阵.即存在可逆阵P使得

其中J1,J2,…,Js为零矩阵或阶数大于1的Jordan块.

情形1所有Ji都是阶数大于1的Jordan块,即

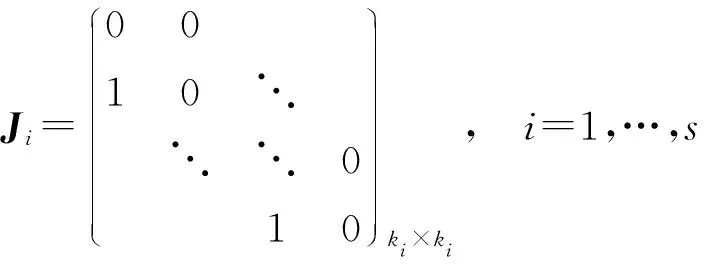
令

那么Mi是幂零阵,Vi是可逆阵,且Ji=Mi+Vi,i=1,…,s.进一步地,记

则M是幂零阵,V是可逆阵.从而

于是,N=P-1MP+P-1VP为一个幂零阵与一个可逆阵之和.

情形2存在Ji为零矩阵,不妨设只有J1=O.由于N是非零矩阵,则J2,…,Js为阶数大于1的Jordan块.记

则

根据情形1,只需证J可以表示为一个幂零阵与一个可逆阵之和即可.因为

为幂零阵,再由文献[5]知,J相似于分块矩阵

注意到

为一个幂零阵与一个可逆阵之和,结论得证.

引理3设A=(aij)为n阶非零方阵.若所有的aii≠0,则A可分解为一个幂零阵与一个可逆阵之和.

证令

则A=N+U.因为所有的aii≠0,所以U是可逆阵.容易验证Nn=O.因而结论得证.

引理4设A是n阶非零方阵.则A为幂零阵或者可逆阵或者相似于准对角阵

其中X1是幂零的且X4是可逆的.

证不妨假设A既不是幂零阵也不是可逆阵.根据文献[6,定理2.1],存在n阶幂等阵E和n阶可逆阵U使得A=E+U,且AE=EA是幂零的.注意到,E≠In且E≠O.由于数域上的幂等阵必相似于对角阵,故存在可逆阵Q使得

其中1≤k≤n-1.

设

其中X1为k阶矩阵且X4为n-k阶矩阵.由于AE=EA,那么有

Q-1AQQ-1EQ=Q-1AEQ=Q-1EAQ=Q-1EQQ-1AQ.

从而

注意到AE是幂零的,所以

是幂零阵,故X1是幂零阵.此外,由于A-E=U是可逆阵,那么

是可逆的.所以X4是可逆阵,结论得证.

2 非零方阵的加法分解

根据文献[4],称环R中的元素a是fine的,如果存在R中一个幂零元b和一个可逆元u使得a=b+u.称满足上述性质的分解为fine分解.由引理2的证明知,fine元是相似不变量.即若a=b+u是fine分解,则对任意可逆元v,均有v-1av=v-1bv+v-1uv也是fine分解.以下给出数域上非零方阵的fine分解.

定理1设A是n阶非零矩阵.则存在n阶幂零阵N及n阶可逆阵U使得A=N+U(即A有fine分解).

证对n作数学归纳法.当n=1时,结论显然成立.

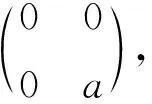
由于a≠0,由引理3知,P-1AP具有fine分解.由此可知A具有fine分解.

假设结论对n-1时成立,下证对n时亦成立.由引理1和引理2,设A既非可逆阵也非幂零阵.根据引理4,不妨令

其中U是可逆阵且N是幂零阵.

若N是非零矩阵,则结合引理1和引理2,结论得证.

若N=O,则

其中U=(uij)为k阶可逆阵.不妨设ukk≠0.再令

为A中右下方的(n-k+1)×(n-k+1)子块.易知,存在变换矩阵P使得P-1WP的(1,1)-元和(2,2)-元均不为零.令

则有Q-1AQ的主对角线上至少有两个元素不为0.由此可记

其中B1,B4为非零方阵.由归纳假设,存在幂零阵Ni及可逆阵Vi使得Bi=Ni+Vi,其中i=1,4.因而

为一个幂零阵与一个可逆阵之和.由数学归纳法,结论对任意正整数n均成立.

注 在定理1中,“非零”的条件是不可缺少的.因为若O=N+U,其中U是可逆阵且N是幂零阵,那么N=-U,矛盾! 定理1的证明过程提供了把非零方阵分解为一个可逆阵与一个幂零阵之和的理论方法.但在实际分解运算中,由于相似变换矩阵P的求解方法缺乏一般性,因而上述分解运算是不易做到的.

推论1任意方阵均可表示为两个可逆阵之和.

证设A是n阶方阵.若A=In,则A=2In+(-1)In为两个可逆阵之和.假设A≠In,则A-In为非零矩阵.根据定理1,存在幂零阵N及可逆阵U使得A-In=N+U.从而有

A=In+N+U=U+(In+N).

注意到,In+N为可逆阵.因此,A为两个可逆矩阵之和.

下面把定理1应用到线性变换中.设V是数域上的有限维线性空间,A是V的线性变换.称线性变换A是可逆的,如果存在线性变换B满足AB=BA为恒等变换;称线性变换A是幂零的,如果存在正整数k使得Ak是零变换[1].

定理2设A是线性空间V的非零线性变换.则A可表示为V中一个幂零线性变换与一个可逆线性变换之和.

证众所周知,在线性空间的一组基下,线性变换与方阵是一一对应的.设η1,η2,…,ηn是线性空间V的一组基,且A在该组基下的矩阵为A,即

A(η1,η2,…,ηn)=(η1,η2,…,ηn)A.

由定理1,矩阵A可表示为一个幂零阵与一个可逆阵之和.记A=N+U,其中N为幂零阵,U为可逆阵.故存在V的线性变换U使得

U(η1,η2,…,ηn)=(η1,η2,…,ηn)U,

即矩阵U在基η1,η2,…,ηn下与线性变换U相对应.易知,U是可逆线性变换.下证A-U为V的幂零线性变换.事实上,

(A-U)(η1,η2,…,ηn)=A(η1,η2,…,ηn)-U(η1,η2,…,ηn)

=(η1,η2,…,ηn)A-(η1,η2,…,ηn)U=(η1,η2,…,ηn)(A-U)=(η1,η2,…,ηn)N.

由于N是幂零阵,易知A-U为幂零线性变换.因此,A=(A-U)+U为幂零线性变换与可逆线性变换之和.结论得证.

结合定理2和推论1,可得如下结论.

推论2线性空间V的任意线性变换均可表示为两个可逆线性变换之和.

3 结 论

矩阵是线性代数中最基本也是最重要的概念之一,是线性代数课程的骨架和贯穿始终的主线.学生对矩阵内容的深层理解是学好线性代数的重要保障.基于线性代数及高等代数教学的积累以及环论研究的经验启示,把环论的相关概念应用到方阵分解上.通过数域上矩阵的性质,证明了任意非零方阵均可表示为一个幂零矩阵与一个可逆矩阵之和的这一主要结论,并应用到线性空间的线性变换上.作为主要结果的推论,得到了任意方阵均可表示为两个可逆阵之和.

致谢作者非常感谢文献[1-8]对本文的启发以及《大学数学》审稿专家的指导意见.