2023年全国乙卷圆锥曲线解法探讨与推广

贺凤梅 李昌成

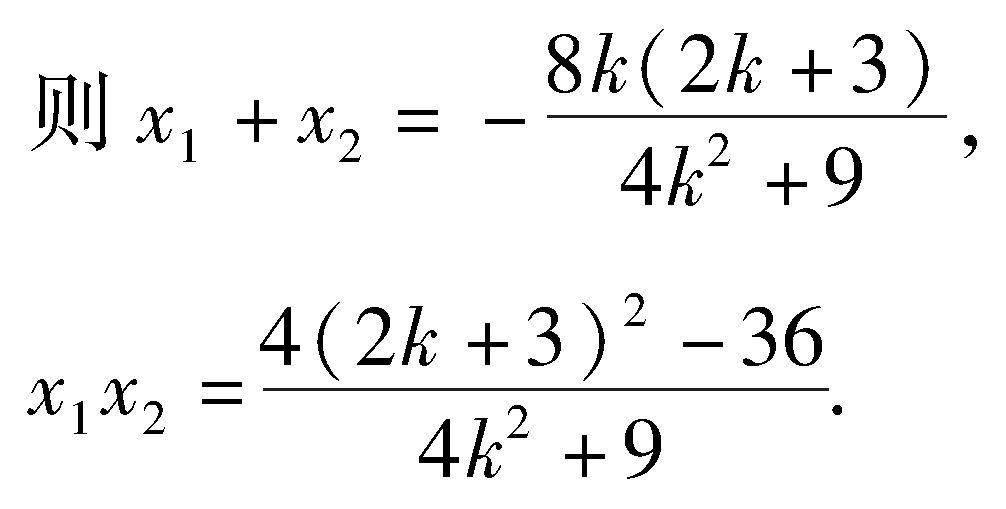
摘 要：圆锥曲线问题是高中数学教学的重点和难点.每年的高考题，都会涉及圆锥曲线问题，既有选择题、填空题，也有作为压轴题的解答题，其特点是综合性和系统性强.这不仅需要学生掌握最基本的知识点，提高运算的速度和准确性，还需要学生能快速找到解题的突破口，成功解答.2023年高考全国乙卷也不例外，这类题充分考查学生的逻辑思维能力、转化与化归能力以及运算求解能力等.

关键词：椭圆；定点；推广

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0057-05

直线与圆锥曲线的综合题一直是高考命题的热点，也是学生学习的难点，大部分学生对这部分知识的学习有畏惧心理.在学习过程中，他们仅停留在记忆相关概念、结论，或者模仿教材和教师的解题思路，并没有真正理解概念、结论的意义，也没有总结圆锥曲线中各种题型的内在关联，或仅仅流于形式，因此考试时往往只能得一部分基础分［1］.据此，以此次高考试题中圆锥曲线的解答为契机，谈谈自己的看法，以期抛砖引玉.

1 题目呈现

（1）求C的方程；

（2）过点（-2，3）的直线交C于P，Q两点，直线AP，AQ与y轴的交点分别为M，N，证明：线段MN的中点为定点.

2 总体分析

此题是2023年全国乙卷的解答题第20题，属于压轴题.这道圆锥曲线题的第（1）问实属常规的送分题，而第（2）问落脚点虽然是定点问题，但与平时训练时见到的题的问法还是有差异.考后笔者了解了一下，在考场上不少考生只是设出直线PQ方程的点斜式，与椭圆方程联立，但由于计算复杂，没有学会合理转化，止步于此了.

其实，直线与圆锥曲线的综合问题，主要是以位置关系为载体，所以根据题意设直线方程，与圆锥曲线进行联立，借助根与系数的关系进行转化求解；同时将问题进行分步拆解，需要设未知量时果断设未知量以及必要的方程，最终设而不求，成功突破.笔者通过思考、解答与总结，尝试厘清问题的本质，现分享于此，以飨读者.

3 试题解答

以下着重探讨第（2）问.

视角1 常规转化.

解法1 （直线的斜截式方程联合求解）

如图1，易知直线PQ的斜率存在，设其方程为y=kx+m，过点（-2，3），所以m=2k+3.①

设P（x1，y1），Q（x2，y2），

消y，整理得

（4k2+9）x2+8kmx+4m2-36=0，

△=64k2m2-4（4k2+9）（4m2-36）>0，

即m2<4k2+9.

由根与系数的关系，得

y1=kx1+m，y2=kx2+m.③

联合③整理，得

将②代入，继续化简整理得

由①

可得m-2k=3.

所以线段MN中点为定点（0，3）［2］.

解法2 （直线的点斜式方程联合求解）

设直线PQ方程为y-3=k（x+2），

即y=kx+（2k+3）.

（4k2+9）x2+8k（2k+3）x+4（2k+3）2-36=0.

不妨设直线AM为y=k1（x+2），令x=0，则y=2k1，所以点M（0，2k1）.

同理N（0，2k2）.

故线段中点坐标为N（0，k1+k2）.

将④代入整理，得

所以线段MN中点为定点（0，3）.

评注 以上两种解法大同小异，解法1设直线PQ的斜截式方程，将点（-2，3）代入，明确数量关系m=2k+3；同时与椭圆方程进行联立，设点的坐标，根据韦达定理得出两根之和與两根之积待用.接着进行下一步转化，结合条件设法将点M的坐标表示出来，再利用同一法表示点N的坐标，进而表示出MN中点的坐标. 此时，随着问题的分步求解，发现本质上就是求两直线AP与AQ的斜率之和为定值.分式进行通分，非对称性转化为对称性，代入韦达定理的式子化简等都属于常规操作.因此，解决问题的关键还是在于我们拿到试题后进行思考、分析、整合，将未知转化为已知，将陌生转化为熟悉，这也是当前新课改后国家选拔人才的要求.解法2只是设直线方程不同，求解路径稍有不同，进行部分分离变量后，式子更简单明了，这也需要通过一定的训练才能达到熟能生巧，灵活变通，不再赘述.

视角2 齐次化转化.

解法3 （平移齐次化求解）

将图象整体向右平移两个单位，则点（-2，3）平移至（0，3），点A（-2，0）平移至（0，0）.

相应直线PQ的方程可设为

y=kx+3，

将平移后的椭圆化简整理，得

齐次化，得

4y2+9x2-36·y-kx3=0.

进一步整理得

从而平移后线段MN中点坐标为（2，3）.

故线段MN中点为定点（0，3），得证［3］.

解法4 （配凑齐次化求解）

将4y2+9x2-36=0进行配凑得

4y2+9（x+2）2-36（x+2）=0.

与直线y=k（x+2）+3联立并整理，得

4y2+（9k+12）（x+2）2-12y（x+2）=0.

故线段MN中点为定点（0，3），得证.

评注 解法3是将点A平移至坐标原点，其余点与直线、椭圆均移至相应的位置，通过齐次化转化，大大减少了运算量. 不过此法建议给学习程度好、学有余力的同学尝试，一定要讲清原理，平移前与平移后的关系，再辅以适当的练习加以巩固，这样才能收到成效. 解法4则是通过构造法整体处理，同样需要老师给学生讲清原理，感兴趣的同仁不妨一试！

视角3 向量法.

解法5 （设线求点及向量共线求解）

设直线AM：y=m（x+2），AN：y=n（x+2），则M（0，2m），N（0，2n），

线段MN中点坐标为（0，m+n），即证m+n为定值.

设P（x1，y1），Q（x2，y2），

（4m2+9）x2+16m2x+16m2-36=0.

易得12m-4m2-9=12n-4n2-9.

又m≠n，所以m+n=3.

故线段MN中点为定点（0，3），得证.

视角4 曲线系.

解法6 （借助曲线系巧妙消元代点求解）

结合解法5，经过三点的二次曲线为

［y-m（x+2）］［y-n（x+2）］=0.

即y2-（m+n）（x+2）y+mn（x+2）2=0.

消去y2，得

显然x≠-2，所以

即PQ的直线方程过点（-2，3），

代入整理并求解得m+n=3.

故线段MN中点为定点（0，3），得证.

评注 曲线系在课本上有涉及，只是平时使用较少，所以大家并不熟悉，从以上解答来看，若能理解、掌握并应用到解题中去，确实有不一样的效果，大家可以根据需要选择！

4 尝试推广

此题的出题背景本质上就是极点极线，可以推广得到以下两个结论.

>b>0），左顶点为A（-b，0），上顶点为B（0，a），过点B（-b，a）的直线交椭圆C于P，Q两点，直线AP，AQ与y轴的交点分别为M，N，证明：线段MN的中点为定点（0，a）.

以上是焦点在y轴上的椭圆的一般结论，对于焦点在x轴上的椭圆的一般结论，大家可以参照得出，不再赘述.

5 试题链接

（1）求E的方程；

简析 该题中的同一法求解是本次真题中所用到的方法，包括直线过定点问题. 只是设置的问题情境不尽相同. 因此，在平时的学习及高考復习备考中，我们一定要关注和积累一些通性通法，所谓万变不离其宗，很多试题均可以追本溯源，不管在知识上还是方法上，都有异曲同工之妙！

简析 该题是比较典型的已知斜率之和为定值，证明直线过定点问题，可以利用文中的常规方法求解，也可以利用平移齐次化或构造齐次化求解. 相信大家只要学会整合与反思，一定能有收获！

6 结束语

高中圆锥曲线的试题对学生思维能力及计算能力的要求都很高，教师在教学时要把握好重、难点，循序渐进，保证学生在夯实基础的前提下，逐步提高难度. 教学过程中，建议结合学生的学情来规划教学的进度和难易程度，耐心细致地解答学生提出的问题及计算中的盲点及卡点. 同时还需要有意识地培养学生的数形结合的能力，从而稳步提高圆锥曲线的教学效率.

命题专家指出，根据《普通高中数学课程标准（2017年版）》的要求，今年高考数学全国卷全面考查考生的数学核心素养，充分体现基础性、应用性以及创新性的考查要求，突出理性思维，发挥数学学科在人才选拔中的重要作用.在全面推行素质教育的今天，新一轮国家教育课程改革之际，对新教材、学生新的学习方式的研究与探讨显得尤为重要. 只有充分发挥青年一代的数学素养，才能提高全民素质，造就新一代的高质量新型人才！

参考文献：

［1］曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，2005.

［2］ 贺凤梅，李冒成.活用定义 巧解圆锥曲线考题：以2022届八省联考第5题为例［J］.数理化解题研究，2022（31）：64-66.

［3］ 贺凤梅，李昌成.多视角探究2022年全国高考甲卷理数第20题［J］.数理化解题研究，2023（28）：2-5.