基于多源量测的主配网一体化状态估计方法
孙 健,李 勇,王秀茹
(1.国网江苏省电力有限公司电力科学研究院,南京 211103;2.国网江苏省电力有限公司宿迁供电分公司,宿迁 223800)
电力系统状态估计是运行人员监测和管控电力系统安全可靠运行的重要工具,其主要通过测量设备获取冗余的量测数据,利用算法估计系统的运行状态。在状态估计的研究中,应用最为广泛的是加权最小二乘法WLS(weighted least squares),该方法以测量值与测量估计值之差的平方和最小为目标函数,并根据量测的精度赋予权重。因为WLS可以不需要随机变量的任何统计特性即可实现较为准确的估计,所以该方法在传统电网中,尤其是输电网实际应用中起到了至关重要的作用,并为电力系统的高级应用提供了有效的电网运行状态数据。
随着电力系统的发展,分布式电源在配电网侧接入使得配电网的随机性与波动性不断增强。运行人员对配电网侧的运行状态愈发重视,各类量测设备被开发与安装,电力系统的通信体系与能力更加的完备。目前,电网已开始大量部署数字继电器、同步相量测量装置PMU(phasor measurement unit)、自动馈线开关以及分布式电源智能逆变器等设备,以提高系统的观测能力,拓宽数据的来源。此外,配电网侧高级计量基础设施AMI(advanced metering infrastructure)的不断部署,实现了定期轮询和按需读取客户间隔需求的功能,丰富了配网低压侧的量测冗余,增强了配电网络的可观测性。这些硬件设施的升级,为实现进一步提高配网的状态估计精度带来了可能。从全局的角度,主配网一体化状态估计有助于从整体上为运行人员提供精确的运行数据,为决策、优化和调度等应用提供数据基础。
目前对主配网一体化的状态估计方法的改进主要集中在算法的收敛性以及量测数据的运用两个方面。针对算法的收敛性,文献[1]提出了Cholesky 三角分解法来提升收敛性能。文献[2]从信赖域的角度为克服病态发散问题提供了解决方案。但上述方法均无法在测量布置不满足全局可观测的情况下保证算法的收敛性以及求解状态估计解的可靠性。在状态估计领域,定义了可观性的概念来表示能否通过已知信息确定系统当前的状态,文献[3]总结梳理了提高配电网可观性的伪量测建模方法。在针对不同尺度的量测数据的混合应用中,文献[4]提出采用部分PMU 量测数据进行状态估计,以提升算法的精度。文献[5]结合数据采集与监视控制系统SCADA(supervisory control and data acquisition)和PMU量测数据,补充量测信息。文献[6]考虑对三相不平衡配电网进行分区,通过改进的区间优化方法求解模型并实现3 种常用量测数据的交互。文献[7]针对混合量测的权重问题,提出迭代更新权重的方式协调混合量测的精度差。文献[8]结合配网的远程终端单元RTU(remote terminal unit)、PMU 和AMI 量测数据,提出将线性静态状态估计与线性动态状态估计相结合,从而加速非线性静态状态估计。上述方法着重于混合量测的精度和时间尺度的配合,并未结合主网和配网进行考虑,即不同网络的不同测量设备所获得的量测数据的协调配合问题。
因此,本文考虑主配网的混合量测条件提出了主配网一体化的状态估计方法,该方法基于动力学系统中的状态估计算法理论。利用该算法能够全局收敛的特性,结合约束模型以实现PMU、SCADA 以及AMI数据在不同观测条件下的协同使用。其中,为有效地实现混合量测的状态估计,建立了局部刷新的极快速状态估计模型和鲁棒状态估计模型,以应对PMU 量测的局部刷新场景和不同类型量测的混合刷新的场景。通过这两种模型的有效结合与协调统一,进一步提出了主配网一体化的状态估计方法,实现主配网量测交互过程中求解运行状态,以有效提升主配网状态估计的精确度与鲁棒性。
1 基于非线性动力学系统的状态估计
首先,本文考虑传统状态估计模型中的非线性测量模型[7],其可表示为
式中:z为测量向量;h(x)为测量和状态变量之间的非线性函数;x为待估计的状态向量;e为测量误差向量。
WLS状态估计模型中,最小化目标函数可表示为
式中:J(x)为目标函数;为误差协方差矩阵;为量测i的标准差,由测量设备的精度决定。
WLS状态估计模型通常利用高斯-牛顿迭代算法进行求解。根据网络结构可获得零功率注入节点信息,该信息有助于提高状态估计结果的准确度。但是零功率注入功率作为准确的测量信息通常被赋予较大的权重,导致量测数据之间权重差距悬殊,从而影响状态估计算法的稳定性。因此,文献[9]基于非线性动力学系统的理论,对传统的状态估计模型建立约束模型。其约束集主要包括由量测与估计值的差值组成的残差约束和由零注入功率信息形成的零注入约束,该约束集可表示为
式中:H(x)为所构建的约束集;hzero_inj(x)为由状态变量计算的零注入的参数方程。
在此约束集的建模基础上,构建相应的商梯度系统[10],其表达式为
式中:=QH(x)为所构造的商梯度系统;DH(x)为约束集H(x)的雅可比矩阵。
文献[9]依据动力学系统理论与残差约束提出定理:当残差约束的每一个加权因子为时,商梯度系统稳定平衡流形对应的能量函数的局部最小值[9]可表示为
式中,E(x)为所构造的能量函数。
可以看出,式(5)与式(2)(即WLS 状态估计模型的最小化目标函数)是等价的。因此,上述定理将求解状态估计解转化为通过积分轨迹追踪动力学系统的稳定平衡流形(即式(4)),其详细证明可参阅文献[9]。由于商梯度动力学系统具有渐近稳定的特性,并且基于动力学系统的状态估计方法在追踪轨迹过程中无需对量测方程的雅可比矩阵求逆。因此该方法具有良好的算法稳定性,并且在量测布置的冗余程度低甚至不满足全局可观的条件下,该方法仍可以计算出有意义的状态估计结果。
文献[11]在上述模型的基础上进一步考虑了高精度测量信息,将PMU 量测作为残差不等式约束添加到WLS模型中,改进后的模型可表示为
式中:hzero(x)为零功率注入信息的平衡方程;β为量测残差约束的边界。
为保证状态估计的结果严格满足约束要求,对式(6)中的不等式添加松弛变量S,产生以下广义的等式约束集,即
式中:H(y)为广义的等式约束集;HE(x)为等式约束集;HI(x,S)为松弛后的不等式约束集。广义状态变量y=(x,S)由待估计状态变量与松弛变量组成,进一步对上述约束集构建相应的非线性动力系统,即商梯度系统[10],可表示为
式中:y为待估计的状态变量与松弛变量的集合;=QH(y)为广义动力学商梯度系统;DH(y)是H(y)的雅可比矩阵。
同理,可知式(8)(即商梯度系统的退化稳定平衡流形)与式(6)的局部最优解等价。因此,可通过式(7)(即追踪状态估计的残差约束集)构建相应的商梯度系统退化稳定平衡流形,求解式(6)。由于商梯度系统中不包含对雅可比矩阵求逆的步骤,在PMU 量测高频率刷新时,即量测不可观的情况下,仍然可以保证得到状态估计解,实现网络运行状态局部更新。若配电网量测信息中含有坏数据,可根据本文所提方法计算出的状态估计结果,利用基于最大正则拉格朗日乘子的不良数据辨识方法对坏数据进行剔除[12],或者采用文献[9]所提出的残差不等式约束模型以及基于动力学系统理论的方法对坏数据进行辨识。
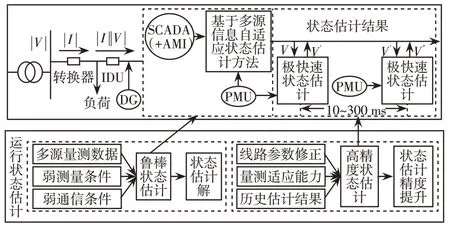
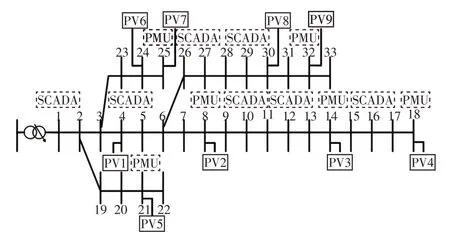
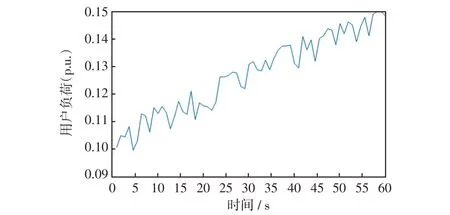
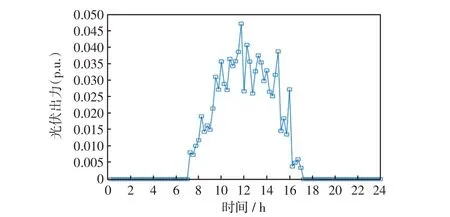
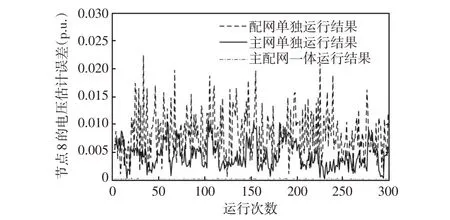
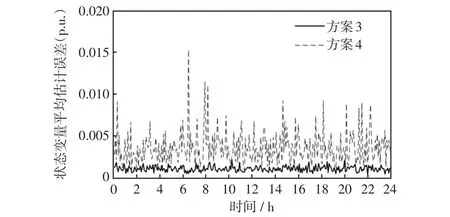
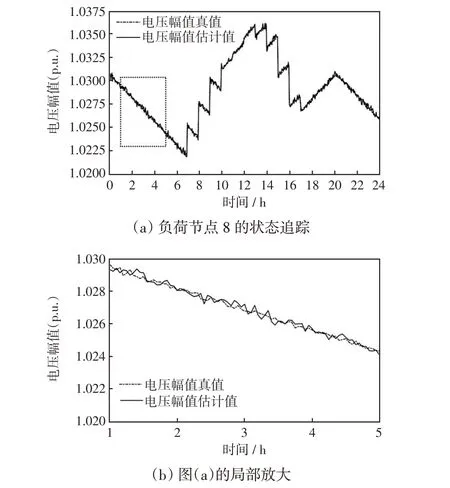
本文在基于动力学系统的状态估计模型上,进一步考虑多源量测的融合问题。为此,根据采集的不同量测数据刷新频率的不同,建立两种状态估计模型,分别为鲁棒状态估计模型和高精度状态估计模型。两种模型的运行配合架构如图1 所示。其中,假设在0时刻,SCADA、AMI和PMU量测均更新采集数据,a表示PMU量测的刷新间隔,b表示SCADA 量测的刷新间隔,c表示AMI 量测的刷新间隔,这3种量测的更新时间间隔关系为a 图1 混合量测的两种状态估计运行架构Fig.1 Running architecture of two-state estimation based on hybrid measurement 首先,当同时采集到SCADA、AMI 和PMU 3 种混合量测数据时,将PMU 量测作为高精度量测计算残差不等式约束添加到状态估计模型中,与SCADA量测和AMI量测残差等式约束形成鲁棒状态估计约束集,即 式中:HR(y)为鲁棒状态估计约束集;zPMU、zSCADA和zAMI分别为PMU、SCADA、和AMI 3 种测量值;hPMU(x)、hSCADA(x)和hAMI(x)分别为对应的量测方程;βPMU为PMU量测的残差约束边界值。 考虑在多源量测刷新过程中,由于PMU 量测的刷新频率较高,使得存在只有PMU 量测和SCADA 量测或PMU 量测和AMI 量测同时更新的情况。在此类情况下,如果不采用加入伪量测的方式,则会使网络量测布置不满足全局可观的条件,进而使传统的基于WLS 的状态估计方法发散而求解失败。但是,此类伪量测的加入会影响状态估计的求解精度[9]。利用基于动力学系统的状态估计方法在不附加伪量测的情况下仍可以稳定求解,因此,在只有PMU 量测和SCADA 量测或PMU 量测和AMI量测同时更新情况下,鲁棒状态估计模型可转化为 式中,HF(y)表示极快速状态估计约束集。 当仅有PMU 量测在局部刷新时,将PMU 量测的残差作为等式约束,与前一更新时刻的SCADA量测和AMI 量测残差作为不等式等式约束形成极快速状态估计约束集,即 式中:βSCADA和βAMI分别为SCADA量测和AMI的残差约束边界值;SSCADA和SAMI分别为对应的松弛变量。 基于上述不同量测条件对应的约束集(式(9)~(11)),构建相应的商梯度系统(式(8)),可根据状态估计解和商梯度系统的稳定平衡流形的一一对应关系,实现通过轨迹追踪稳定平衡流形获得不同量测条件下的状态估计解。 上述鲁棒状态估计模型和极快速状态估计模型的不同之处在于,针对采集量测不同的特性,采用不同的建模方式。在鲁棒状态估计中,由于PMU量测是高精度量测,则为此类量测设置较小的残差边界值,可在求解状态估计问题最优解的基础上保证PMU 安装节点的状态估计质量。而在极快速状态估计中,所采集到的量测只有PMU 量测。PMU负责局部估计以更新准确的运行状态,同时结合前一更新时刻的SCADA 和AMI,为其设置较大的残差边界值,可作为全局估计范围的补充。在极快速状态估计模型中,以前一时刻的状态估计值作为初点,可实现快速通过轨迹追踪到当前状态估计解并完成局部状态估计更新,因此称其为极快速估计模型。 基于多源量测的状态估计方法的具体流程如图2 所示,其根据不同时间尺度的量测条件由2 种模式组成:第1 种模式为量测集中刷新模式,其主要融合更新的SCADA、PMU和AMI量测,根据更新量测情况构建鲁棒状态估计模型(式(9)或(10)),实现高精度全局估计;第2种模式为PMU局部刷新模式,其利用局部更新的PMU 量测数据和历史量测数据,构建极快速状态估计模型,以准确地更新局部关键节点的状态。 图2 融合SCADA、PMU、AMI 量测等多源数据的配电网高精度鲁棒状态估计示意Fig.2 Schematic of high-precision robust state estimation of distribution network based on multi-source data measured by SCADA,PMU and AMI 具体方案的执行步骤如下。 步骤1输入更新的混合量测数据与网络参数数据。 步骤2判断混合量测的类型并获取零注入节点功率信息。 步骤3对各项量测计算残差并形成鲁棒状态估计约束集和极快速状态估计约束集(式(11))。 步骤4构建相应的商梯度系统(式(8)),通过积分轨迹追踪稳定平衡点以获得当前时刻状态估计结果。 在融合多源量测的状态估计方法基础上,本文进一步考虑了网络结构,提出主配网一体化的状态估计方法。为给高级应用分析提供准确的估计信息,主网与配网测量信息融合并共同用于状态估计计算,从而提高估计结果精度。但由于配网规模的不断扩大,主配网集中式状态估计存在一定的计算负担。同时,混合量测尺度不同的问题难以保证状态估计结果的准确性。因此,本文提出主配网一体化状态估计方法,其中假设主网的主要量测为SCADA 量测,配网的量测数据为各个负荷节点的AMI量测数据和稀疏的PMU 量测数据。主网主要基于SCADA量测进行状态估计,其估计结果可为配网主节点状态提供准确估计信息。配网则结合主网估计的主节点状态,并基于AMI 量测和PMU 量测进行状态估计,其结果与主网进行交互。主配网量测交互迭代求解,可以避免整体估计的维数灾难问题,且有助于提升估计结果的精度和鲁棒性。 由于主网的量测类型和更新频率与配网的量测不一定相同,在考虑主配网之间的配合时需要对量测的混合设置进一步细化,其主配网量测估计信息交互流程如图3 所示。当主网布置的SCADA 量测更新时,结合配网传输的主配网连接点处的状态估计信息,即将主配网交互节点电压作为高精度伪量测,采用基于动力学系统的状态估计方法更新主网的估计结果,同时修正主配网连接点处的状态信息。同理,当配网的PMU 量测处于更新的状态且AMI量测没有更新时,结合主网传输的主配网连接点处的状态信息,配网采用极快速状态估计,对配网进行局部的状态估计并更新;当PMU量测和AMI量测几乎同时更新时,同样结合主网传输连接点处的状态信息,并将PMU 量测作为高精度量测,采用鲁棒状态估计模型对配网的全部节点状态进行高精度估计并更新。配网状态估计结果更新的同时,对主配网连接点处的信息起到了修正作用。通过主网和配网的状态估计对连接点状态信息的不断利用与修正,从而实现主配网的估计信息交互以及一体化状态估计。 图3 主网和配网状态估计信息交互流程Fig.3 Flow chart of state estimation information interaction between transmission and distribution networks 本小节在接入光伏的IEEE-33 节点系统上对混合量测的状态估计方法进行测试以验证其有效性,其光伏装置的详细网络布点如图4 所示。其中,在此网络节点系统的基础上,在8、14、18、21、25和32 节点接入采集周期为300 ms 的PMU 量测,设置该类量测的随机噪声标准差为0.000 1;在1、4、10、12、16、26和29节点配置SCADA量测,采集周期设置为6 s,量测类型包括各节点的注入功率、支路功率和电压幅值,设置该类量测的随机噪声标准差为0.01。此外,各个负荷节点均配置AMI 量测设备,采集周期设置为15 min,量测类型为负荷节点的注入有功功率和无功功率,设置该类量测的随机噪声标准差为0.03。 图4 IEEE-33 节点系统布置量测Fig.4 Measurement configuration in IEEE 33-node system 该算例中,首先考虑1 h尺度的状态估计,负荷波动设置为随时间在区间[0.8,1.2]之间变化,其中节点4的负荷变化曲线如图5所示。在此运行条件下,对比以下2种状态估计方案。 图5 负荷曲线Fig.5 Load curve 方案1:当配网中仅有PMU 量测更新时,采用本文提出的极快速状态估计模型(式(11));当PMU量测、SCADA量测和AMI量测混合更新时,将PMU量测作为高精度量测,利用鲁棒状态估计模型(式(9))进行计算。 方案2:当仅有PMU 量测更新时,采用WLS-高斯牛顿法并结合PMU 量测和负荷伪量测进行状态估计;当PMU量测、SCADA量测和AMI量测混合更新时,不可观的节点采用伪量测补充,并根据不同的量测精度设置权重,利用基于WLS-高斯牛顿法状态估计进行混合量测的状态估计。 上述2 种方案的状态估计结果如图6 和图7 所示,其中图6为1 h的估计误差对比结果,图7为1 min的对比结果。从图6 可以看出,在1 h 内混合AMI、SCADA和PMU不同时间更新的量测条件下,所提状态估计方法(方案1)的估计结果误差均低于方案2,因此具有更好的应用效果。从图7 可以看出,在1 min内仅有SCADA和PMU更新的量测条件下,极快速状态估计方法在SCADA 刷新的间隙中实现局部刷新状态估计结果的同时,可以保持较好的估计精度,因此,相较于常规的WLS-高斯牛顿方法具有一定的优势。 图6 1 h 的估计曲线Fig.6 Estimation curves for one hour 图7 1 min 的估计曲线Fig.7 Estimation curves for one minute 本算例采用由主网的IEEE-14 节点和配网的IEEE-33 节点联结而成的主配网系统,分别如图8和图9所示,验证所提出的主配网一体化状态估计方法的有效性。此外,分别在配网的节点8布置光伏电站,其以15 min为采集周期的24 h光伏出力曲线如图10 所示。由于配网的负荷性质较为复杂,对系统中此类节点状态信息的准确性要求很高。假设主网的主要量测为SCADA 量测,且每个节点均布置有SCADA 量测,配网的主要量测为AMI 和PMU量测。配网AMI和PMU的布置位置与第4.1节中的算例相同,不同的是主节点的状态信息来自主网SCADA量测的估计结果。 图8 IEEE-14 节点主网算例Fig.8 Example of IEEE 14-node transmission network 图9 IEEE-33 节点配网算例Fig.9 Example of IEEE 33-node distribution network 图10 光伏出力曲线Fig.10 PV output curve 为说明主配网一体化状态估计的必要性,观察主配网的连接节点8在3种不同的主配网状态估计方法下的电压估计误差,结果如图11所示。第1种运行方式为单独运行主网的状态估计,其中节点8连接的负荷量测取伪量测值,其随机误差服从高斯分布(标准差设置为0.08)。可以看出,该方法在配网负荷波动时,主网节点8的估计精度不稳定。第2 种运行方式为单独运行配网状态估计,节点8 作为配网的主节点,由于缺乏主网电压的更新信息,使用配网的量测信息对其进行估计,这使得该节点的估计误差相对较大。第3 种运行方式采用理想的主配网状态信息交互,量测同步的形式。从结果可以看出,节点8 的电压估计精度明显提高。然而,根据实际应用情况,主网与配网的状态估计之间存在量测时间差和精度差。因此,本小节将提出一种主配网一体化的状态估计方法,并与集中式状态估计方法进行对比。两种方案具体的执行方式如下。 图11 主配网连接点不同方案运行结果Fig.11 Operation results under schemes with different connection points between transmission and distribution networks 方案3:配网运行状态估计时,主节点的信息为上一时刻主网更新的估计信息,当配网中仅有PMU量测更新时,采用极快速状态估计;当配网中的PMU 和AMI 量测更新时,将PMU 量测作为高精度量测,利用鲁棒状态估计进行计算。在主网运行状态估计时,若主网的SCADA量测得到更新,则结合配网状态估计的结果对主网提供结果,利用基于动力学系统的状态估计方法完成主配网的交互。 方案4:采用集中式的状态估计方法,通过WLS-高斯牛顿方法进行状态估计。在该方案施行过程中,主配网量测的配置与更新进程与方案3是相同的。但是,由于基于牛顿法的WLS方法需要对量测方程的雅可比矩阵求逆,仅采用更新的混合量测会使得配网在AMI 更新的间隙无法满足全局可观的条件,从而导致基于牛顿法的WLS方法因量测方程的雅可比矩阵出现奇异而求解失败。因此,为保证系统的冗余度,需要利用随机误差服从高斯分布(标准差设置为0.08)的负荷伪量测数据,并对该伪量测设置较小的权重来参与状态估计。 在24 h 的时间尺度下,方案3 与方案4 的状态估计结果对比如图12 所示,从结果可以看出本文所提的鲁棒状态估计与极快速状态估计结合的主配网一体化的估计精度远高于集中式的状态估计方案。进而对配网中连接光伏电站的节点8 的电压幅值的估计结果进行观察,并以3 min 为采集间隔对比24 h内的电压幅值的估计值与真值的差距,结果如图13 所示。其中图13(a)为原图,图13(b)为时间范围为1~5 h 的局部放大,具体放大位置已在图13(a)中标出。从图中可以看出,电压幅值的估计结果与真值接近,表明在实现主配网一体化状态估计的同时,可实现实时状态的追踪,有助于提供准确的光伏节点状态信息。 图12 状态估计误差对比Fig.12 Comparison of state estimation errors 图13 配电网络中的负荷节点8 的状态追踪Fig.13 State tracking of No.8 load bus in distribution network 本文提出了一种融合PMU、AMI 和SCADA 多源量测的主配网一体化的状态估计方法。所提方法基于非线性动力学系统的状态估计模型,继承该模型全局收敛的优点,可用于不同更新频率的多源量测条件下的状态估计。由于所提方法不需对量测方程的雅可比矩阵求逆,因此在系统量测不满足全局可观的条件时仍然能够计算出有意义的解,这体现了基于动力学系统理论的状态估计算法的鲁棒性。在兼顾PMU 量测的局部高精度估计和融合多源量测的鲁棒估计的同时,进而考虑利用主网与配网不同量测信息的协同互补,实现对主配网一体化状态的高效估计。所提的状态估计方法在主配网一体化系统中进行了测试,验证了算法的可靠性和有效性。 为更切合实际应用,考虑系统规模较大的网络,可以参考文献[9]所提出的算法流程,即首先利用WLS-高斯牛顿方法进行状态估计计算,其计算结果可作为初值点,进而利用本文所提出的基于动力学系统理论的状态估计方法对状态结果进行进一步的精度提升,此混合式的算法流程使得状态估计应用兼顾计算速度和精度。同时,配网侧的三相不对称的网络模型情况,以及对光伏、风电等高渗透率分布式电源作为新型伪量测对状态估计结果精度影响等因素均亟需加入到状态估计算法开发中。此外,随着电力系统的发展,还需进一步有针对性地考虑新型伪量测,未来这些工作均将在本文工作基础上进一步地进行完善。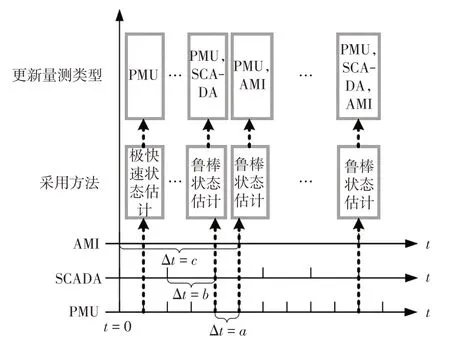
2 基于多源量测状态估计方法
3 主配网一体化估计方法

4 算例分析
4.1 混合量测状态估计方法测试
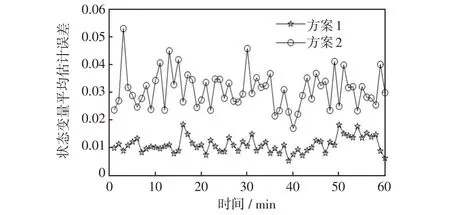
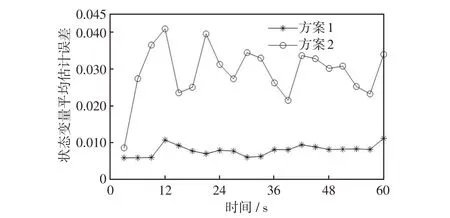
4.2 主配网一体化状态估计测试
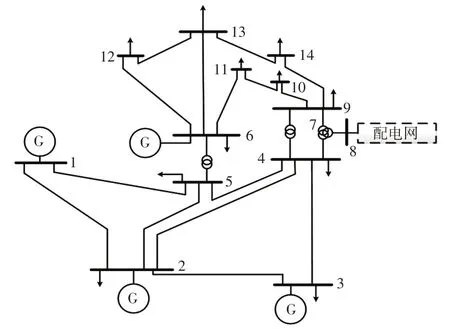
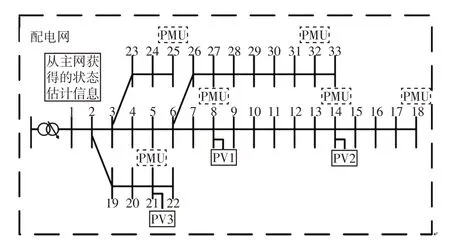
5 结 语

