布鲁纳儿童认知发展阶段论指导下的小学数学教学

摘 要：布鲁纳将儿童认知的发展分为动作表征、形象表征和符号表征三个阶段。前一阶段是后一阶段的基础，三者不能相互替代；前面阶段不会因为后面阶段的出现而完全消失，三者可以共同存在。数学学习的本质是学习数学化，而数学化就是在具体、半具体半抽象、抽象之间的铺排，也是穿行于实物与符号之间的形式化过渡。因此，可以根据布鲁纳的认知发展三阶段论设计小学数学教学，使学生经历数学化的过程。对此，需要高度重视、充分利用形象表征。

关键词：小学数学；布鲁纳；认知发展阶段；认知表征

本文系2020年度江苏省社科基金后期资助项目“教师发展指导者研究”（编号：20HQ054）、江苏省教育科学“十四五”规划2021年度课题“指向核心素养的义务教育阶段数学探究教学设计研究”（编号：D/2021/01/156）的阶段性研究成果。

布鲁纳是美国著名心理学家、教育学家，是将心理学理论应用于教育的典型代表。他对认知过程进行过大量的研究，提出了包括儿童认知发展三阶段论在内的众多经典教育理论。儿童认知发展三阶段论提出至今已有50余年，对今天的中小学数学教学仍有重要的指导意义。

一、布鲁纳儿童认知发展阶段论概述

布鲁纳的儿童认知发展三阶段论是在继承和批判皮亚杰认知发生论的基础上，总结认知发展实验的结论而提出来的。布鲁纳认为，儿童智力的发展表现为再现模式的变化，根据儿童再现表象所依据的媒介不同，将儿童认知的发展分为动作表征、形象表征和符号表征三个阶段。[1］

动作表征是指用动作来表达关于世界的知识和经验的表征方式。这种方式也被称为动作再现模式，具有高度操作性。它主要表现为一个人知道怎样去做某件事情，是由一套适合得到某种结果的行动构成的。动作表征是儿童认知发展的第一阶段，是幼儿认识外界事物的主要方式，在成人的认知活动中也自始至终发挥作用。

形象表征是指用图形或意象来再现知识和经验的表征方式。它相当于皮亚杰儿童认知发展阶段论描述的“具体运算水平”的认知活动，即依赖于事物的外部特征或事物在头脑中的表象来认识和掌握事物。形象表征出现在动作表征之后，是儿童认知发展的第二阶段，在６至７岁儿童的认知活动中表现得最为明显，在儿童期后的认识活动中也一直发挥重要作用。

符号表征是最高级的表征形式，就是用词汇和语言的形式建立的表征，具有高度生成性和概括性。符号表征阶段，无思维的行动和知觉性的理解被符号系统取代，复杂的经验和思想被简缩成精练的语言或符号，使信息更容易从记忆中检索与提取。

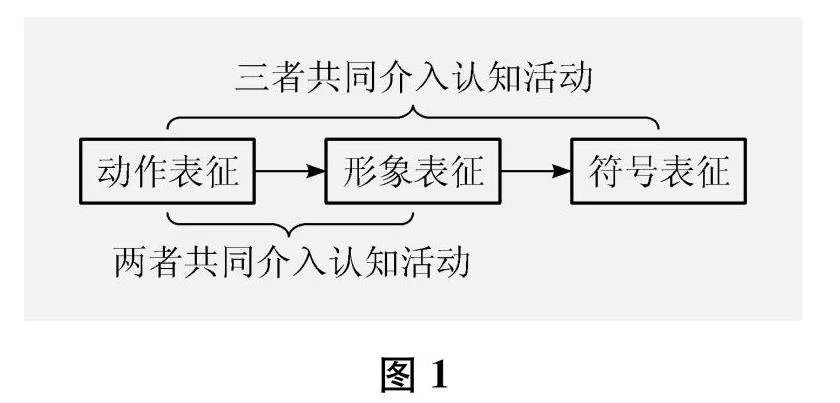
动作、形象和符号是人们借以知觉、认识、保持和再现外界事物的三种不同的表征方式，分别代表儿童认知发展的三个不同阶段。一方面，前一阶段是后一阶段的基础，三者不能相互替代。另一方面，前面阶段不会因为后面阶段的出现而完全消失，三者可以共同存在。因此，布鲁纳的儿童认知发展三阶段论可以用图1来表示。

在整个小学阶段，第一学段（1—2年级）学生以动作表征为主；第二学段（3—4年级）学生以形象表征为主，同时兼有动作表征；第三学段（5—6年级）学生以符号表征为主，同时兼有动作表征和形象表征。其中，形象表征阶段是一个非常重要的阶段，它起着承上启下的作用。事实上，心理学的相关研究表明，小学第二学段是从具体形象思维向抽象逻辑思维转换的关键期。

二、布鲁纳儿童认知发展阶段论运用于小学数学教学的典型案例

根据布鲁纳的儿童认知发展三阶段论设计教学，就是要关照各个阶段学生的认知发展特点，引导学生选择恰当的方式来表征知识经验和思维过程，助力学生的知识理解和思维发展。荷兰数学家、数学教育家弗赖登塔尔认为，数学学习的本质是学习数学化。顾泠沅教授认为，数学化就是在具体、半具体半抽象、抽象之间的铺排，也是穿行于实物与符号之间的形式化过渡。因此，可以根据布鲁纳的认知发展三阶段论设计数学教学，使学生经历数学化的过程。对此，需要高度重视、充分利用形象表征，因为它具有半具体半抽象的特点，是具体和抽象的中介，是从实物到符号过渡的关键。［2］这一思想可以贯穿小学数学教学的始终，指导很多重要内容的教学。下面针对“数与代数”知识、“图形与几何”知识和解决实际问题的教学，呈现几个典型案例。

【案例1】 “退位减法”的教学［3］

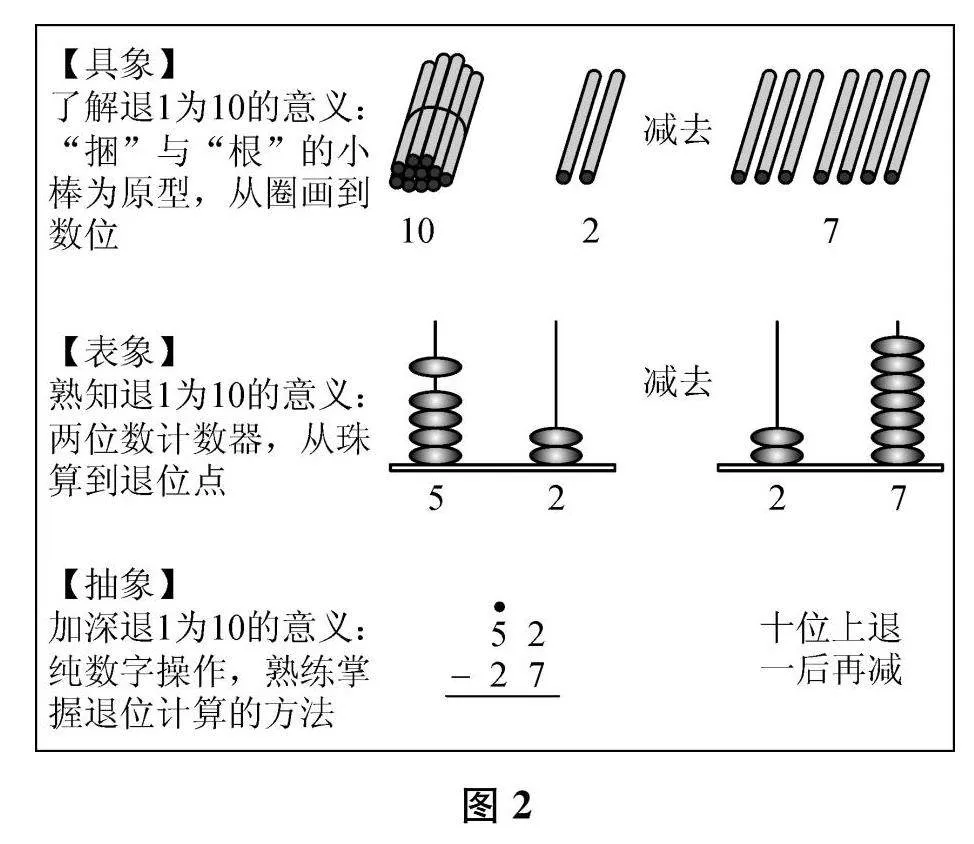
两位数退位减法的基础是10以内数的分与合和20以内数的加减，延伸内容是简便运算、连续退位减法和隔位退位减法。在这一系列内容的学习过程中，学生对算理“退一当十”的理解经历从了解到熟知再到加深的过程。对于两位数的减法（包括退位减法），美国著名教育心理学家加涅等制作过一个机械化操作的流程图。［4］该流程图忽视了人脑和电脑的区别，学生经过这样的机械操作过程是无法理解算理的。关于两位数的退位减法，根据布鲁纳的儿童认知发展三阶段论，可以设计如图2所示的教学过程：学生初学整数的加减时，如学习10以内数的分与合、20以内数的加减时，可以用小棒、小方块等具象的学具说明算理；学习两位数的退位减法时，学生的认知已经达到表象水平，因此再用具象的学具来解决问题是认知的倒退，可以用半具体半抽象的计数器说明算理，从而帮助理解抽象的符号运算52-27。

【案例2】 “有余数的除法”的教学［5］

“有余数的除法”的教学，教师一般让学生用乘法口诀进行试商训练，这种程式化的训练忽略了学生对试商意义的理解。其实，可以充分利用学生的生活经验，设计如图3所示的“分豆子”情境，引导学生经历三个阶段的活动：首先是具体的实物操作——分豆子，然后是半具体半抽象的表象操作——脑中分豆子，最后是抽象的符号操作——数式运算。其中，“脑中分豆子”是使学生越过从实物到符号的鸿沟的中介。经历这样的数学化过程，学生不仅深刻理解了有余数的除法，而且找到了运算规律。

【案例3】 “长方形和正方形的周长与面积”的教学［6］

教学长方形和正方形的周长与面积时，教师往往就事论事，强调公式的记忆和运算的操练，而忽略学生对原理的理解，造成学生容易出现混淆周长与面积的错误。教材将周长与面积分开教学，但这不能从源头上解决问题。实际上，周长与面积计算的实质分别是一段一段和一块一块相加（测量），在这个基础上推导出公式。相对来说，面积公式的得出较为复杂。教学时，可以设计比较长方形和正方形面积的情境，引导学生经历“具象地用实物数方格—表象地在脑中数方格—抽象地用公式计算”的三阶段探究过程，从而帮助学生充分理解面积计算的实质，区分面积计算与周长计算。

此外，关于周长与面积，学生还存在“图形的周长长，面积就大”的错觉。为了使学生彻底弄清楚周长与面积的关系，沪教版小学数学教材（三年级下册）设计了两个探究活动：一是用12根火柴棒围出不同的图形，比较谁的面积大，得出关于周长相等时图形面积最大情况的结论；二是用20根火柴棒围出不同的长方形，得出“在周长相等的情况下，长和宽越接近，长方形面积越大；当长和宽相等，即长方形成为正方形时，面积最大”的结论。这两个问题实际上是等周问题的雏形。但是实际探究过程中，学生用火柴棒或小棒围图形时，容易出现歪斜的问题，很难摆出方正的图形来。实际上，根据布鲁纳的认知发展三阶段论，学生在初步认识周长与面积时，可以借助一些具象的操作来理解概念，如用绳子量周长、数小方块求面积等；而在研究周长与面积的关系时，因为对周长与面积的认识已经达到表象水平，所以可以采用在虚线方格纸上画图形这种表象操作的方法。虚线方格纸不仅能防止歪斜现象，而且限定了单位，便于比较。

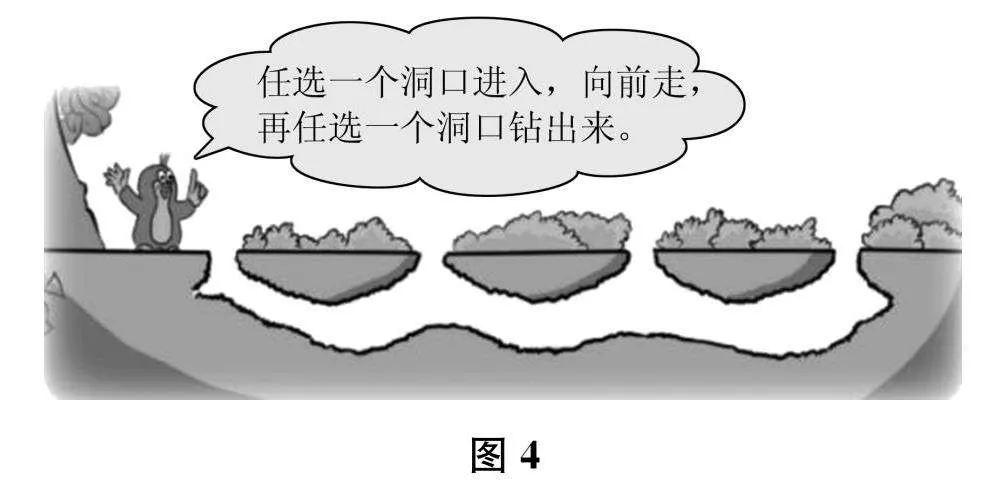
【案例4】 “数图形的学问”的教学

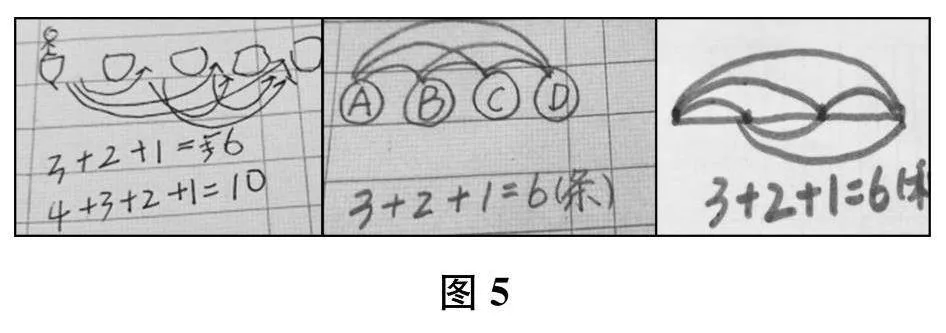
“数图形的学问”是北师大版小学数学四年级上册的内容，属于简单的组合问题。教材首先从“鼹鼠钻洞”的情境（如图4所示）出发，让学生探究“鼹鼠有几条跑动路线”，引出四点组合问题；然后通过“菜地旅行”的情境，拓展到五点及更多点的组合问题。教学中，对于第一个问题情境，学生通常会出现三种做法：在情境图上画并数路线、画示意图并数路线和直接列式计算。其中，第二种方法通常占大多数，并且具体有如图5所示的三种。这里，第一种方法是具体的动作表征，第二种方法是半具体半抽象的形象表征，第三种方法是抽象的符号表征。对此，教师可以抓住第二种方法，引导学生经历“求鼹鼠跑动路线条数”到“数线段条数”再到“列式计算”的数学化过程。

最后需要指出的是，利用布鲁纳的儿童认知发展三阶段论指导小学数学教学，需要谨防“认知倒退”的现象，比如：学生对某些内容的认知已经达到抽象阶段，不需要再借助具象了，教学活动却仍然通过实物操作来完成［7-8］，不但繁复费力，而且没有成效。

参考文献：

［1］ 范燕莹.世界著名教育思想家布鲁纳［M］.北京：北京师范大学出版社，2012：3.

［2］ 俞宏毓，朱向阳.充分利用表象，使学生经历数学化——《数图形的学问》一课教学与思考［J］.教育研究与评论（小学教育教学），2021（8）：8993.

［3］ 顾泠沅.课堂视野中的教师及其指导者［R］.上海：未来十年中国数学教育展望学术研讨会议，2013.

［4］ R.M.加涅，W.W.韦杰，K.C.戈勒斯，等.教学设计原理（第五版）［M］.王小明，庞维国，陈保华，等译.上海：华东师范大学出版社，2007：139.

［5］ 顾泠沅，王洁.教师在教育行动中成长——以课例为载体的教师教育模式研究（上）［J］.课程·教材·教法，2003（1）：915.

［6］ 俞宏毓.“长方形和正方形的面积与周长”教学指导研究报告［J］.数学教育学报，2014（3）：7175.

［7］ 俞宏毓，朱向阳，顾泠沅.管窥小学数学课堂教学现状——“两位数减两位数退位减法”教学案例分析［J］.数学教育学报，2019（1）：4348.

［8］ 俞宏毓，潘勇.教师发展指导者工作的案例研究——以“异分母分数的加减法”教学指导为例［J］.教育学术月刊，2013（7）：103105+111.