在分割图形中全面认识“对称性”

摘 要：苏教版小学数学教材《多边形的面积》单元的一个“动手做”活动，让学生通过分割图形的操作，感受平行四边形等图形的中心对称性。对此，教学时，可以融入更多学生学过的图形，设计如何将图形分割成完全一样或者大小相等的两份的情境问题，并且从轴对称图形过渡到中心对称图形、从对称图形过渡到不对称图形、从常规图形过渡到组合图形，从而引导学生全面地认识图形的对称性，并逐渐深化对图形对称性的理解。

关键词：小学数学；“动手做”；分割图形；对称性；图形的运动

一、教前思考

苏教版小学数学五年级上册第二单元《多边形的面积》中新授内容“梯形的面积”（例6、例7）后安排了一个“动手做”活动（如图1所示）。

其中，先指明平行四边形的中心；再让学生通过分割图形的操作，感受平行四边形的中心对称性；最后让学生通过操作方法的迁移，感受正方形、长方形、正六边形的中心对称性——不需要知道中心对称和中心对称图形的概念。

教师教学用书指出，本活动的编写意图是，通过对一些常见平面图形有趣性质（规律） 的探索，加深学生对相关平面图形基本特征以及面积含义的认识，进一步提高对“图形与几何”的学习兴趣。［1］但笔者进一步分析有关内容后，发现其教学价值不止于此。

中心对称（点对称）和轴对称（线对称）、平面对称（面对称）是图形反射变换的三种重要形式。反射和旋转、平移是图形全等变换的三种重要形式。因为是全等变换，所以旋转和平移的结果也具有某种“对称性”（一般来说，旋转的结果具有的是旋转对称性。实际上，平移的结果具有的是“周期性”，但“周期性”也可以看作一种广义的对称性）。特别地，中心对称既是线上的反射变换（对应点连线被中心平分），也是面上的旋转变换（绕中心旋转180度）；轴对称既是面上的反射变换（对应点连线被对称轴垂直平分），也是空间的旋转变换（绕对称轴旋转180度）。进一步地，全等（保距）和相似（保角）是图形变换的两种基本形式。［2］在义务教育数学课程的“图形与几何”领域，图形的变换（运动）不只是独立的主题，而更是研究图形的性质（认识）的一种视角。［3］这主要反映在作为变换对象与结果的多个或单个图形所具有的与变换有关的关系或性质中。

关于图形的变换（运动），学生在小学主要初步学习平移、旋转和轴对称，知道平移、旋转、轴对称变换前后图形的形状、大小不变（即三者都是全等变换），能找出两个图形之间的平移、旋转或轴对称关系，知道一些图形本身的轴对性，但还不了解图形本身的中心对称性以及旋转对称性、“平移对称性”。在《多边形的面积》单元，推导三角形和梯形面积公式时，发现两个完全一样的三角形或梯形可以拼成平行四边形——这里孕伏着平行四边形的中心对称性。

在此基础上，安排这个“动手做”活动，让学生感受中心对称图形的特点，可以进一步完善学生关于图形变换的知识结构，并为初中学习中心对称乃至旋转对称做铺垫。

为了实现这样的教学价值，可以拓展教材给定的图形，融入更多学生学过的图形，并且改变教材直接给出图形分割方法的做法，设计如何将图形分割成完全一样的两份的情境问题，延伸至如何将图形分割成大小相等的两份的情境问题，引导学生自主探究常见图形的对称性，全面地认识图形的对称性。同时，可以从轴对称图形过渡到中心对称图形、从对称图形过渡到不对称图形、从常规图形过渡到组合图形，引导学生自然地展开探究，逐渐深化对图形对称性的理解。这样，就将本活动设计成一节规律探究课。

二、教学过程

（一）分割轴对称图形，复习轴对称性

师 今天，河东村的村委会特别热闹，很多村民聚在一起，讨论分田地的问题。你问他们为什么要分田地？原因很多，有的是想分给自己的子女，有的是想分开种不同的蔬菜……不管这些原因，他们遇到的问题都是：如何把自己家的田地分成完全一样，即大小相等、形状相同的两块？

（出示一个长方形）

牛大叔家田地的形状是长方形，该如何分呢？请同学们在材料袋中找出长方形纸片，试着分一分。

（大多数学生都通过“将纸片对折，然后画出折痕”的方法来分。）

师 老师发现，大家基本上都采用了对折的方法。为什么这样分成的两部分完全一样呢？

生 对折后两部分完全重合，所以它们完全一样。

师 很好！大家还记得对折后完全重合的图形是什么图形吗？

生 轴对称图形。

师 不错。我们学过，长方形就是轴对称图形，还记得它有几条对称轴吗？在纸上画出来。

生

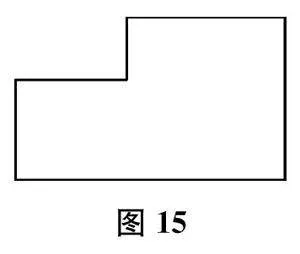
（展示画法，如图2）

两条，一横一竖。

师 很好！所以，牛大叔家的田地有这两种分法。

（出示一个正方形、一个等腰三角形、一个等边三角形、一个等腰梯形、一个正五边形、一个正六边形）

通过这样的方法，你还能分一分马大婶等村民家的田地吗？

生 正方形、等腰三角形、等边三角形、等腰梯形、正五边形、正六边形也都是轴对称图形，找到它们的对称轴，就能把它们分成完全一样的两部分了。

师 很好！同学们就来找一找这些图形的对称轴吧。尽量找全哦。可以小组合作。

（学生小组合作找对称轴。）

生

（出示图3—图8）

他们分别有4条、1条、3条、1条、5条、6条对称轴。

师 正方形也就是正四边形，等边三角形也就是正三角形。由此，你发现正多边形对称轴的条数有什么规律？

生 正几边形就有几条对称轴。

设计贴近生活的问题情境，先出示学生熟悉的轴对称图形，让学生将其分成完全一样的两部分。提供纸片材料让学生操作，有利于学生激活思维，回忆蕴含“完全一样的两部分”要素的轴对称图形概念，从而获得“基于轴对称性质找对称轴”的分割方法。在此基础上，按照学生学习的顺序出示常见的轴对称图形，引导学生复习它们的对称轴画法，顺便总结正多边形对称轴条数的规律。

（二）分割中心对称图形，感受中心对称性

师

（出示一个平行四边形）

王老汉家田地的形状是平行四边形，你会分吗？

生

（脱口而出）

找对称轴。

生 不对，平行四边形不是轴对称图形。

师 是的。四年级在《平移、旋转、轴对称》单元，我们学过：平行四边形不是轴对称图形。该怎么办呢？请同学们在材料袋中找出平行四边形纸片，试一试。

（学生尝试。）

生

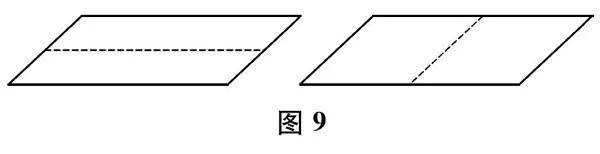
（展示分法，如图9）

平行四边形和长方形有点像。可以横着画一条线或斜着画一条线，把它分成两个完全一样的小平行四边形。

师 你是怎么确定这条线的位置的？

生 我用直尺量出平行四边形左边这条边的长度，平均分成两份，找到中间一点；再量出右边这条边的长度，也平均分成两份，找到中间一点；然后把这两个中点连起来，就画出一条横的线。同样地找中点，也可以画出一条斜的线。

师 看来，你是类比长方形，因为没法通过对折的方法来找对称轴，所以采用了测量长度平分的方法来画分割线。为什么这样的分割线能将平行四边形分成两个完全一样的小平行四边形呢？

生

（同步操作）

沿着这样的分割线剪开，两个小平行四边形完全重合。

师 注意说明你的操作。之前是通过对折让两部分完全重合，现在呢？

生

（若有所悟）

通过平移。

师 是的。而且必须剪开，因为不剪开没法平移。

（稍停）

还有不同的分法吗？

生

（展示分法，如图10）

我还有不同的方法，既不用量，也不用算，只要画出平行四边形的一条对角线，就能把平行四边形分成两个完全一样的三角形。

师 你怎么知道这样分成的两个三角形完全一样？

生 推导三角形的面积公式时，我们曾用两个完全一样的三角形拼出平行四边形，拼法就是让一组相同的边靠在一起成为一条对角线。因此，可以利用对角线把平行四边形分割成两个完全一样的三角形。

师 活学活用，真棒！当然，这还只是道理上的说明。眼见为实，你能验证一下这两个三角形完全一样吗？注意说明你的操作。

生

（同步操作）

沿着对角线剪开，

（略微迟疑）

通过……旋转，可以让两个三角形完全重合。

师 很好！能具体说一下是怎样的旋转吗？

生

（再次操作）

一个三角形不动，另一个三角形绕着这条分开的边的中点旋转180度。

师 非常好！受到“分成两个完全一样的三角形”这种方法的启发，你还能想到什么方法？

生 分成两个完全一样的梯形。推导梯形面积公式时，我们曾用两个完全一样的梯形拼出平行四边形，拼法是让一组相同的腰靠在一起。

师 那怎么找到这条分割线，即这组相同的腰呢？

生 分析拼成的平行四边形与原来的梯形的关系，发现：平行四边形的一组对边分别是由梯形的上底和下底按不同的顺序连接而成的。于是我们想到，只要在一组对边的两端分别量出相等的长度，找到两个对应的点，再把这两个点连起来，就能把平行四边形分成两个完全一样的梯形。

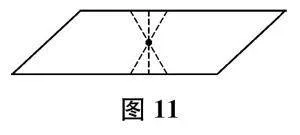
（展示分法，如图11）

因为量出的长度可以不同，所以画出的分割线也不止一种。我们画出了三条分割线，并且发现：三条分割线相交于一点，这一点是三条分割线的中点。

师 同样地，请你验证一下两个梯形完全一样。

生

（同步操作）

沿着分割线剪开，一个梯形不动，另一个梯形绕着这条分开的腰的中点旋转180度，可以让两个梯形完全重合。

师 非常好！“分成两个完全一样的梯形”的方法，让我们一下子多了无数种将平行四边形分成完全一样的两部分的具体方法。

（稍停）

从上述分法中我们发现，有些图形虽然不能通过对折完全重合，即不是轴对称图形，但是可以通过平移或旋转180度完全重合——当然，平移和旋转图形的一部分需要把图形剪开。另外，老师很好奇，既然旋转后重合的分割方法有无数种，包括画对角线分割的方法，那么包不包括画横着和斜着的线分割的方法？

（学生尝试发现，图9中的两种分法也可以通过绕着分割线的中点旋转180度，让两个小平行四边形完全重合。）

师 很好！你们发现了将平行四边形分成完全一样的两部分所有方法的共同点：分割后可以通过旋转180度实现完全重合。老师还有一个疑问：有同学发现“分成两个完全一样的梯形”方法中的三条分割线相交于同一点，即它们共同的中点，那么其他分法的分割线也过这一点吗？这一点也是这些分割线的中点吗？

生

（展示做法，如图12）

我们验证了，发现是这样的。

师 由此，你有什么猜想？

生 过这一点任意画一条线，都能将平行四边形分成完全一样的两部分。

师 你的数学感觉很好！结论是正确的。到了初中，你们不仅可以验证它，而且可以证明它。

（稍停）

这样，将平行四边形分成完全一样的两部分的关键就是找到这一点。怎么找呢？需要在边上测量长度吗？

生 不需要，这一点其实是平行四边形对角线的交点。

师 你的发现很有价值！其实，平行四边形对角线的交点就是平行四边形的中心。过中心任意画一条线，都能将平行四边形分成完全一样的两部分。这是因为平行四边形是中心对称图形。初中，你们会进一步学习这个概念的。现在，请大家回头去看之前分割的轴对称图形，哪个图形也有中心对称的性质，也能被过中心的任意一条线分成完全一样的两部分？它的中心在哪里？先观察猜想，再操作验证。

（学生小组合作研究，发现：长方形、正方形、正六边形有中心对称的性质，其中心都是对角线的交点；等腰三角形、等边三角形、等腰梯形、正五边形没有中心对称的性质。）

师 好的。还是聚焦正多边形，你发现其对称性有什么规律？

生 边数为偶数的正多边形既是轴对称图形，也是中心对称图形；边数为奇数的正多边形是轴对称图形，不是中心对称图形。

师 很好！数学中有很多的规律等着我们去发现。

（稍停）

现在再来想一想：我们学过的图形还有哪些？它们是轴对称图形吗？是中心对称图形吗？请在材料袋中找出纸片，观察、操作。

（学生活动。）

生 我们还学过直角三角形、锐角三角形、钝角三角形以及一般角三角形。如果它们不等腰或等边的话，就既不是轴对称图形，又不是中心对称图形。

生 还学过直角梯形和一般梯形。一般来说，它们也既不是轴对称图形，又不是中心对称图形。

师 很好。这些既不轴对称又不中心对称的图形是没法被分成完全一样的两部分的。不过，它们可以被分成大小相等的两部分。至于怎么分，同学们可以课后去研究。

本环节让学生将非轴对称而中心对称的平行四边形分成完全一样的两部分，聚焦本课新知，是教学的重点。学生发现平行四边形不是轴对称图形，不能迁移运用轴对称图形的分法。教师提到《平移、旋转、轴对称》单元，是在暗示学生可以从平移、旋转的角度看问题。学生一时没有领会，而通过类比长方形和联想三角形、梯形面积公式的推导方法，发现了分割的方法。教师提出验证的要求，引导学生关注其中的平移与旋转操作，从而逐步发现多种分法的共同点：分割后可以通过旋转180度实现完全重合；分割线交于它们共同的中点，也就是旋转时所绕的点。由此，找到分割平行四边形的一般方法，自然地引出中心和中心对称的概念。进而，让学生迁移运用这种方法研究上一环节分割的图形，通过观察和操作，发现轴对称图形有些是中心对称图形，有些则不是。顺势，让学生发现其他学过的图形既不是轴对称图形，也不是中心对称图形，并课后研究这样的图形如何被分成大小相等的两部分。由此，帮助学生比较全面地认识常见图形的“对称性”（全等分割）以及“可平分性”（等积分割）。基于控制课堂教学容量和减轻学生学习负担的考虑，正多边形的旋转对称性就不提，更不深究了。

（三）分割组合图形，综合应用中心对称性

师

（出示图13）

王老汉说：“我家的田地是分给我两个儿子的。地里有一个自动喷水装置，在图中点P的位置。这个装置两个儿子都想要，怎么办呢？”

生

（画出平行四边形的对角线，找到平行四边形的中心O，连接OP，得到图14）

自动喷水装置正好在两块地的分界线上，就可以两家共用了。要使两块地完全一样，分界线要经过平行四边形的中心。两点确定一条直线，所以，把平行四边形的中心O与自动喷水装置所在的位置P连起来，就得到两块地的分界线了。

师 很好！在中心对称图形中，过中心点的无数条线都可以把图形分成完全一样的两部分。现在分割线还要经过另外一点，所以就只有一条了。

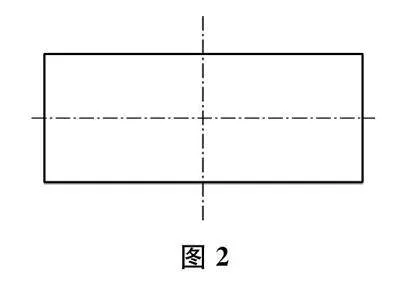
（出示图15）

张奶奶家田地的形状是这样的，可以分成完全一样的两块吗？

（学生观察、操作后发现：它既不是轴对称图形，也不是中心对称图形，所以不能分成完全一样的两部分。）

师 那么，它能分成大小相等的两块吗？

（学生尝试。）

生

（展示分法，如图16）

我将这个图形分成了上下两个长方形，然后分别画出这两个长方形的对角线，找到它们的中心。经过这两个中心画一条线，就能将这个图形分成大小相等的两部分了。

生

（展示分法，如图17）

我的方法和他差不多：我把这个图形分成了左右两个长方形，然后分别找到它们的中心。经过这两个中心画一条线，也能把这个图形分成大小相等的两部分。

师 现在，这样分成的两部分形状不同。那么，它们大小相等吗？为什么？

生 相等。因为这条线经过两个长方形的中心，所以，两个长方形都被分成了大小相等的两部分。而这个图形被分成的两部分都是由两个长方形的一部分组成的，所以，它们大小相等。

师 很好！确实，这里可以不操作验证，而直接应用我们之前发现的图形的中心对称性质来说明道理。这就是知识的价值。

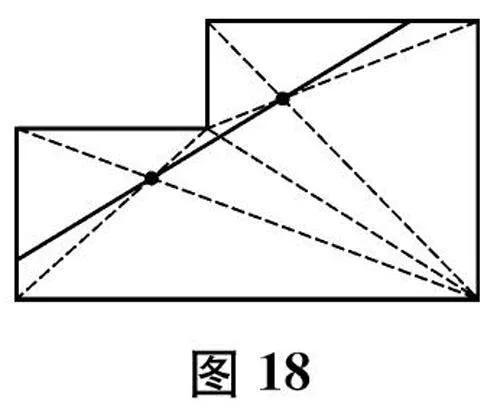
生

（展示分法，如图18）

我觉得，还可以将这个图形分成两个梯形，分别画出这两个梯形的两条对角线，找到它们的中心，然后经过这两个中心画一条线，把这个图形分成大小相等的两部分。

生 不对！梯形不是中心对称图形，没有中心。而且，很明显，分出的图形左边小、右边大，面积不相等。

生 啊。我忘记了。

……

本环节让学生应用常规图形的中心对称性分割组合图形，完成“旧知复习—新知探究—新知应用”的学习闭环，认识到几何图形的复杂性、多样性以及分割方法的简明性、一般性，体会到看似简单的知识更为广泛的应用价值。这里，分割有一个特殊点要考虑的平行四边形，为分割更为复杂的组合图形做好了分割线“从动到定”的铺垫。

参考文献：

［1］ 南京东方数学教育科学研究所.义务教育教科书·数学教师教学用书（五年级上册）［M］.南京：江苏凤凰教育出版社，2016：35.

［2］ 吴正宪，刘劲苓，刘克臣.小学数学教学基本概念解读［M］.北京：教育科学出版社，2014：328349.

［3］ 吕世虎，颜飞.新课标“图形与几何”内容分析：从结构到要求［J］.教育研究与评论（中学教育教学），2022（10）：9.