探寻“动手做”数学课程生长的实践路径
芮金芳

在新修订的苏教版教材中,新增了“动手做”版块,成为它的一大亮点。笔者统计分析发现,全套教材12册,共安排了37个“动手做”活动。六个年级的“动手做”活动或巩固新知,或游戏实践,或实验探索,或拓展思维,或渗透思想等,由易到难、由浅入深,精心设计、系统安排,各个活动既基于具体的教学目标与内容,又适应学生身心发展的实际,是我们组织学生做数学的很好资源。
“动手做”作为一块新的课程内容,需要我们深入挖掘、整体设计,寻求有效的课程生长实践路径,提高“动手做”课程活动的水平和品质。真正引领学生在活动中做数学,在活动中触摸数学的本质,深化数学的思维,体验数学的奇妙,生长数学的思想,从而彰显它独有的一片风景。
一、深度整合,实现文本嫁接
在课程实施中,作为教师必须具有整体结构化的课程视野,大胆实践开发课程的意识,才能有效引领儿童深度建构知识,让学习真实发生。
在“轴对称图形”教学中,教师从整体上把握教学内容,巧妙引用“动手做”中剪纸这一传统民间手工艺作为引子,组织学生在动手“剪”的活动中感受轴对称图形的核心特征,将有形的技法渗透于无形的操作感悟之中。同时,将“创作设计”轴对称图形作为补充内容纳入课程范畴,学生根据学与做的深度融合,其学习行为将不仅仅停留在教师给定的规定动作和行为模式上,而是力求在材料的选择、操作的方式上进行自主化的选择,最终达成个性化的实践成果。
这样的文本整合处理,向学生展现了“动手做”课程中蕴含的丰富内涵,为学生提供了动手实践的机会,弥补了教材中预留的空白,让学生进一步理解数学核心内涵、欣赏数学之美、积累数学学习经验,让原本乏味的数学课堂充满情趣、充盈滋味。同样,进行“平移和旋转”“认识平行四边形”教学时,也可以相机穿插“动手做”中的实践活动,将新知识探究与动手做完美融合起来。
二、历史补白,凸显思维内核
在大数据信息背景下,目前的数学教学已经出现学生基础学力过剩的现象,但在高等级思维能力的形成和培养上存在缺陷。这就迫切需要我们转变数学学习方式,丰富数学学习课程资源,我们不仅要把眼光聚焦现有的文本资源,更要拓宽自身课程视野,追溯知识的历史渊源,理清知识的来龙去脉,为真正提升学生综合数学素养寻找可能的切入点。
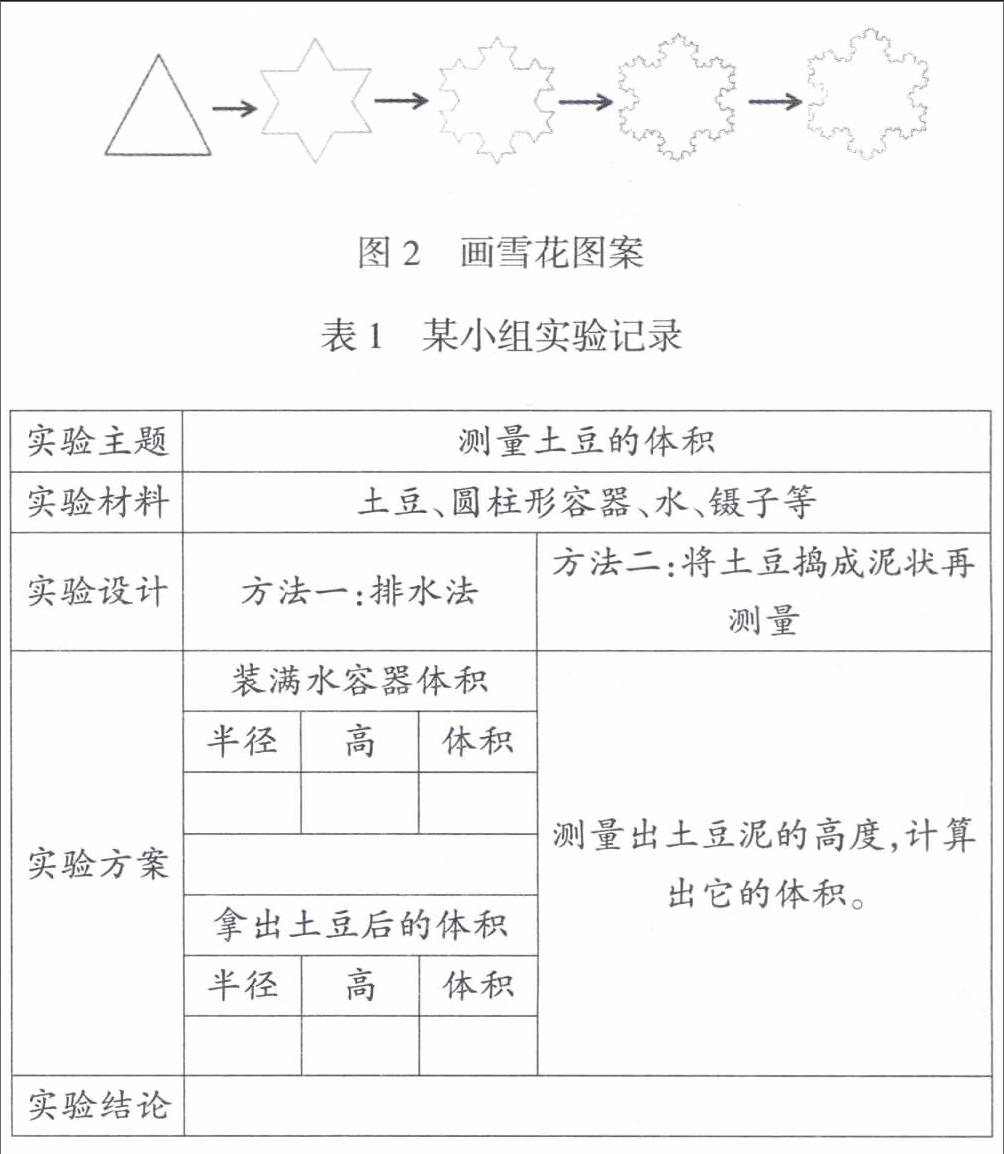
苏教版《数学》四年级下册在“认识三角形”后,安排了一次“动手做”——画雪花图案(图2)。许多教师理解教材的常规解读脉络为:分析画法—演示操作—实践体验—适当评价。
如果把教学目标仅定位在画出雪花图案上,这样的教学缺乏思维生长的触点,无法展现“动手做”课程内容的多姿多彩,限制了学生多样化认知的视角,所以我们要多方位深度思考,挣脱教学活动的束缚,进行有效的拓展与延伸。
资料一:这个美丽的几何分形是由瑞典数学家赫尔奇·冯·科克在1904年创作的,因为其形状类似雪花而得名“雪花曲线”。
资料二:雪花曲线有两个迷人的特性——
雪花曲线周长是无限的。
雪花曲线面积是有限的,它是原来那个生成它的三角形面积的五分之八。
资料三:1975年美籍数学家伯诺瓦·芒德勃罗创立分形理论,当时它被认为是“数学怪物”,是不入数学研究主流的“病态”图形。随时间推移,分形已成为一门严肃的数学分支。美国物理学家约翰·惠特曾说:“可以相信,明天谁不熟悉分形,谁就不能被认为是科学上的文化人。”
资料四:分形的实例——起伏跌宕的地貌、弯曲的海岸线、浮动的云朵、飞扬的雪花、杂乱无章的粉尘、无规则运动的分子、原子的轨迹、万物生长和演化……都具有分形的特点。
在课程历史回溯的过程中,学生领悟到数学知识发展中深刻的数学思维,感受它背后蕴含的丰富的数学思想价值。“雪花曲线”中分形技术的不断演变过程,渗透“简单中孕育着复杂”的深刻哲理,使得学生的辩证思维得以发展。学生在这样的课程价值引领下,动手做不仅获得一种方法、策略,更是建立起对数学的一种博大的情怀、一种深刻的思维方式,一份内在独特的数学感受。
三、实验探究,累积活动经验
根据统计分析,我们发现在“动手做”专题课程内容里有很多富有探究意味的数学实验活动。可以设计成片段式的小实验,也可以开发、培育具有完整主题性的大实验项目。实验完整流程的设计是数学实验的核心,也是实验成败的关键。一般按照“提出实验问题—制定实验方案—实施实验步骤—分析实验现象—分享实验成果—形成实验报告”的流程开展实验活动。
苏教版《数学》六年级下册“圆柱和圆锥”后面的动手做中安排了一次测量不规则物体体积的主题实验活动。教师提供具有典型探索性的实验素材,如土豆、核桃、鸡蛋、圆柱形容器等,作为探索模型来研究不规则物体体积的核心方法。以下是某小组实验单记录情况。
学生在提供的多样化素材的反复实验过程中,不断观察、发现、质疑、调整实验方案。对实验获得的数据结果或产生的实验现象深入分析、思考,回应实验初提出的假设或猜想。如测量核桃的体积,出现多次实验数据不完全相同的情况时思考:怎样做能将实验的误差调整到最小?除了改进实验器材外,有学生提出可以多次实验,获得实验数据后再计算平均值。学生从原先粗糙的模糊估计逐渐发展为数学化地分析处理结果,这是学生在动手数学实验中实现自身操作经验与思考经验的完美融合,他们完整经历实验、发现、推理、直觉、验算、结论的每一个过程,真正获得解决问题的实验方法,让数学智慧获得生长的可能。
四、游戏体验,滋长自由精神
游戏是一种自由活动,好玩、快乐是它的本色。游戏是儿童独有的一种生命状态和存在方式。数学就是一种游戏。在玩中学、学中玩是儿童喜爱的一种数学课程存在方式。在“动手做”的课程建设中,了解儿童内在的学习需求,了解他们喜欢的数学游戏种类,每个年段中的“动手做”都可以开发、设计出符合儿童年龄特征、凸显核心目标的数学游戏。
低段学生以具体形象思维为主,可以设计“图形拼组游戏”“智玩七巧板”“多彩折纸游戏”“魔方游戏”等,学生通过动手操作、识图辨形,提升他们的思维想象力,培育良好的审美观点。高段的学生以逻辑抽象思维为主,设计“图形分割游戏”“天平平衡游戏”“数独游戏”等,进一步丰富、发展逻辑推理能力,提升高层次思维水平。
以“智玩七巧板”为例,它是广泛流传于民间的数学游戏。虽只有简单的7块板,但学生对这种数学游戏的探索着迷并且创造出许多令人惊讶的成果。由于参与游戏的好奇心和它独特的“魔力”吸引,学生会从自身智力水平出发,乐此不疲地向纵深学习。学生除了明白常规七巧板的多种玩法,还了解到“曲线七巧板”,并尝试拼搭成有意思的动物图形:马、蝴蝶、鱼、鸟等。更有甚者还了解知晓了我国民间流传的一种立体七巧板,挑战了更有难度、更复杂的立体结构模型。
在这样的做、玩、学中,学生可以深刻感受几何构图的精巧优美,以及我们祖先创造的不朽智慧。动手做与数学游戏的完美融合,让数学的精神在游戏中悄悄浸润儿童的心灵,突破常规、不断挑战、大胆创新、自由创造,真正促使教育在游戏与儿童身上悄然发生。
在“动手做”的课程视野下,我们能够感受到儿童不仅获得知识的涵养、数学能力的提升,更让他们体验到数学思考的美妙、数学思想的深远、数学创造的乐趣,还孕育出非数学学科特有的创造能力、动手能力、实践能力、合作能力等,最重要的是,他们开始“做”,并“会做”,且快乐地“做数学”。
参考文献
[1] 郑毓信.数学思维与小学数学[M].南京:江苏教育出版社,2008.
[2] 张维忠.文化视野中的数学与数学教育[M].北京:人民教育出版社,2005.
[3] 约翰·杜威.经验与教育[M].北京:人民教育出版社,2005.
[4] 董林伟.初中数学实验教学的理论与实践[M].南京:江苏科学技术出版社,2013.
[5] 谢明初.数学教育中的建构主义:一个哲学的审视[M].上海:华东师范大学出版社,2007.
[责任编辑:陈国庆]

