精准构建几何思维 创设高效数学课堂

陈晓静

摘要：数学思维的训练对于学生学好数学这门学科至关重要，特别是发散性思维能够开拓学生的思路、培养学生灵活的学习思维，让学生在解题过程中不局限于一个解题方法。本文主要从一题多解、一题多问、一题多变等方面来阐述怎样培养学生的发散思维。

关键词：初中数学 几何数学  发散思维

发散思维就是从已知条件、规律、方法、概念出发，对问题的解决不按常规，而产生另一种或多种想法的思维方式。发散性思维可激发发学生的学习动机、启迪思想、激发求知欲、探索欲和创新欲等。因此，在初中数学几何教学中，鼓励他们勇于创新、发散思维，使得学生从多方面、多层次以及多角度进行思考，探索出独特、新颖、简单的解题方法是非常重要的。

一、一题多解，激发学生的求知欲

思维循规蹈矩是学生发散思维培养的主要障碍，如果学生的思维积极性较强，则有利于发散思维的培养。通过一题多解的方法让学生从不同角度思考问题、解决问题，可以引起学生强烈的求异欲望，培养学生思维的灵活性以及求同存异的思维能力。

案例1  已知，AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE。

点拨  一般来说，“证明两条线段的和等于第三条线段”时，常用的方法是截长补短法。截长法是指在第三条线段即最长的线段上截取一段等于较短两条线段中的一条，然后再证最长线段上所剩的部分，等于两条短线段中的另一条。补短法是指把两条较短线段接起来，然后证所得的最长线段等于第三条线段；根据这种思路我们就有两种证明方法。

证明一  如图1，在AE上取点F，使EF=BE，

由CE⊥AB有，△CEF≌△CEB，

∴ ∠CFE=∠B

∵ ∠B+∠D=180°

∴ ∠CFA=180°－∠CFE=∠D

∵ AC平分∠BAD

∴ △ADC≌△AFC

∴ AD=AF

∴ AE=AF+FE=AD+BE

证明二   如图2，延长AD到点F，使AF=AE，

由AC平分∠BAD，易证 △AFC≌△AEC

∴ ∠F=∠AEC，CF=CE

又∵ CE⊥AB

∴ ∠CEB=∠AEC=90°

∴ ∠F=∠CEB

∵ ∠B+∠ADC=180°，∠FDC+∠ADC=180°

∴ ∠CDF=∠B

∴ △DCF≌△BCE

∴FD=BE

∴ AF=FD+AD=BE+AD

即AE=AD+BE

通过一题多解，可以加深学生对题目的形式、组成元素以及题目隐含的逻辑（因果）关系的认识，从而培养了学生数学洞察力和推理能力，更重要的是培养了学生的发散思维，有利于学生今后在解决数学问题时拓宽解题思路，提高解题的灵活性。

二、一题多问，培养学生的发散性思维

要培养学生的发散性思维，首先要改变学生固有的思维模式，从多角度进行思考，这也是学生思维的求异性。要训练以及培养学生抽象思维能力，就要注重培养思维的求异性，让学生从多个角度来分析问题，最终探索出一条简便、新颖的解题思路。

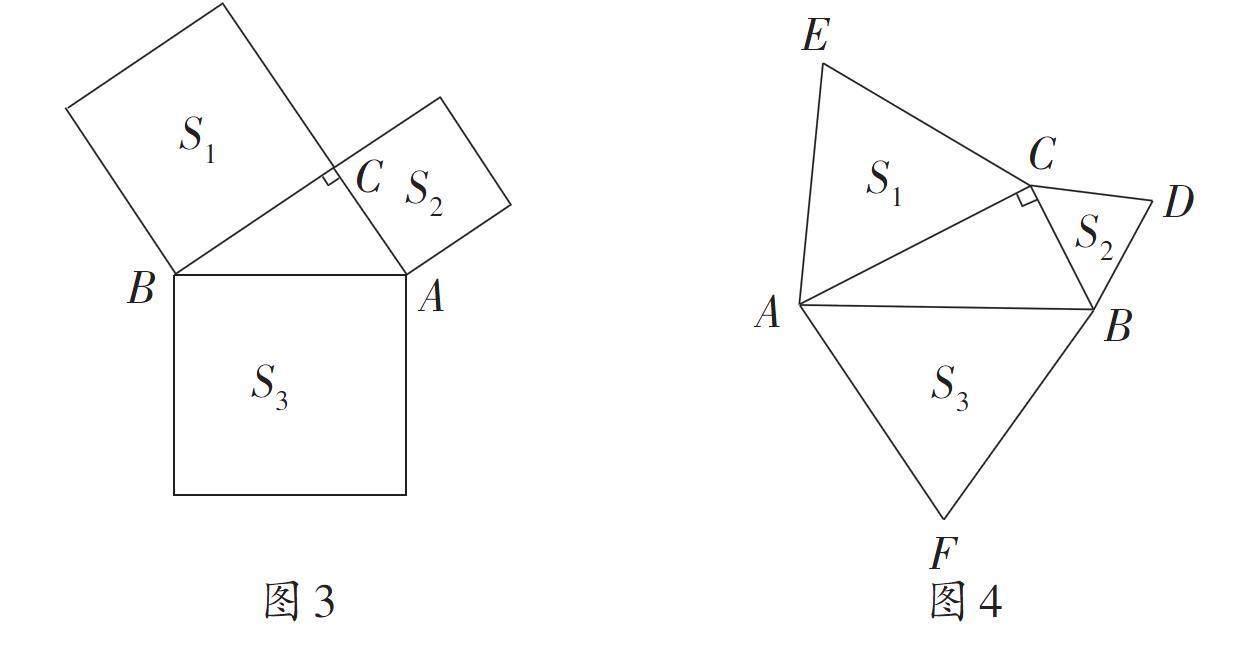
案例2 上完八年级上册“2.7探索勾股定理”内容后，我安排了从勾股定理到图形面积关系的拓展，我们知道，勾股定理反映了直角三角形三条边之间的关系：a2+b2=c2。而a2，b2，c2又可以看成是以a，b，c为边长的正方形的面积，因此，勾股定理也可以表述为：分别以直角三角形两条直角边为边长的两个正方形的面积之和，等于以斜边为边长的正方形的面积，如图3，即S1+S2=S3。

如果以直角三角形的三条边a，b，c为边，向外分别作正三角形，那么是否存在S1+S2=S3呢？如图4，引导学生根据正三角形的面积公式，得到

S3=[34c2]，S1=[34a2]，S2=[34b2]

∵ △ABC是直角三角形，

∴ a2+b2=c2

经过分析，发现以直角三角形的三条边a，b，c为边向外分别作正三角形，同样能得到S1+S2=S3。

类似地，上述结果是否适合其他图形呢？分别以直角三角形的三条边a，b，c为边向外分别作半圆，作等腰直角三角形，则S1+S2=S3依然成立吗？再画几个类似的图试一试。

通过上述这么多问题的探讨，学生的思维得到了更好的拓展，分别以直角三角形ABC三边为一边向外作相似图形，其面积分别用S1、S2、S3表示，则S1+S2=S3都成立 。

三、一题多变，培养学生的思维广阔性

思维广阔性是发散思维的一大特征，在初中几何数学教学过程中，通常有一些学生对于知识一知半解，在解决问题时往往存在一定的片面性，要改变这种狭隘性思维，老师在课堂上应该对同一类型的题目进行引申和多解，让学生分组讨论，如此不但拓宽了学生解题思路，也使得他们的发散思维得到培养。

案例3  已知，如图5，在△ABC中，点D，E分别在AB，AC边上，F是CD中点，连BF交AC于点E，∠ABE+∠CEB=180°，判断BD与CE的数量关系，并证明你的结论。

结论：BD=CE

证明  延长BF至点G，使FG=BF，连CG，

∵ F为CD中点，  ∴ CF=DF

在△GFC和△BFD中，

FG=BF，∠GFC=∠DFB，CF=DF

∴ △GFC≌△BFD（SAS）

∴ ∠CGF=∠FBD，CG=DB

又∵ ∠ABE+∠CEB=180°，∠CEG+∠CEB=180°，

∴ ∠CGF=∠CEG

∴ CG=CE    ∴ BD=CE

变式  已知，如图6，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD。求证：AD=CE。

证明  作DG∥BC交AC于G，如图所示，则

∠DGF=∠ECF，

在△DFG和△EFC中，

∠DGF=∠ECF，∠DFG=∠EFC，FD=EF，

∴ △DFG≌△EFC（AAS），

∴ GD=CE，

∵ △ABC是等边三角形，

∴ ∠A=∠B=∠ACB=60°，

∵ DG∥BC，

∴ ∠ADG=∠B，∠AGD=∠ACB，

∴ ∠A=∠ADG=∠AGD，

∴ △ADG是等边三角形，

∴ AD=GD

∴ AD=CE

这两个题目从本质上看，是比较相似的，然而单独拿出来给学生做的时候，学生却不知道该如何下手，所以在教学中将这个题目安排在一起，通过变式的形式让学生寻找它们的本质，从而让学生的数学思维得到更好的发展。