雪花形二维耦合振动夹心式压电超声换能器的设计

许 龙, 王威震, 龚 涛, 李 果, 赵 伦, 周光平, 梁召峰

(1. 中国计量大学 理学院, 杭州 310018; 2. 深圳职业技术大学 智能制造技术研究院,广东 深圳 518055;3. 西安邮电大学 西安市先进控制与信息处理重点实验室,西安 710121)

纵向振动夹心式压电换能器由于其结构简单、性能稳定、机电转换效率高等优点而被广泛应用于超声清洗、超声加工、超声焊接等技术中[1-5],甚至已经渗透到了医疗、国防和航空航天等高科技领域中[6-8]。压电微机械超声换能器(piezoelectric micromachined ultrasonic transducer,PMUT)通过制造足够小(半波长)的二维阵列实现多向辐射,在传感、驱动及成像等低功率需求中有着一定的应用前景[9-10]。然而,随着超声技术的发展,在大功率超声方面,对换能器的功率容量、振动模式、声辐射面积和声辐射方向提出了不同的要求,传统的纵向振动夹心式压电换能器已不能满足新的应用需求。为了提高换能器的功率容量和超声振动强度,通常采用将多个半波长的夹心式换能器级联组成多激励结构[11]或者采用功率合成技术将多组压电陶瓷堆或多个夹心式纵向振动换能器并联排列或互成角度排列成多头结构夹心式压电换能器系统[12]。无论是多激励级联式换能器还是多头换能器,虽然有效提高了输入电功率和超声辐射强度,但由于其工作在高阶谐振模式,机电转换效率会有所降低。为了增大纵向夹心式压电换能器的声辐射面积,一类纵径复合振动的push-pull管换能器和环形换能器在液体处理领域获得了广泛应用[13-14]。为了改善传统纵向振动换能器的声辐射方向,Itoh等提出了L-L[15]、L-L-L[16]和R-L[17]振动方向变换器,许龙等人提出了一种可实现二维四向超声辐射的双模复合振动压电换能器[18]。Khmelev等[19]设计了一种径轴复合压电超声换能器,实现了换能器在较高的频率下具有较大的功率容量。

为了进一步提高换能器的功率容量和实现单个换能器多方向超声辐射,本文提出了一种雪花形二维耦合振动夹心式压电超声换能器。通过特殊的结构设计实现二维六向超声辐射,改善了传统一维纵向振动换能器的超声辐射面积和一维声辐射问题。首先,基于耦合振动理论和机电类比原理,建立了雪花形二维耦合振动夹心式压电超声换能器的等效电路模型并推导了其共振频率方程。其次,利用等效电路法设计了不同纵向尺寸的雪花形夹心式压电超声换能器,通过有限元软件Comsol对换能器的振动特性进行了仿真模拟。最后,加工制作了相应的换能器试验样品,测试了换能器的频率-阻抗特性以及振动性能,等效电路法、有限元仿真和试验测试取得了较为一致的结果。本文提出的雪花形二维耦合振动夹心式压电超声换能器通过纵向耦合共振模式,在传统纵向振动换能器结构简单、性能可靠的基础上实现了单个换能器多向声辐射的特点,有望于多维超声加工、多向超声辐射等领域中获得应用[20]。

1 理论分析

1.1 结构及振动原理

图1为雪花形夹心式压电超声换能器的结构示意图和试验样品,该换能器由正六棱柱形金属块、6组压电陶瓷晶堆和6个圆柱形金属盖板组成雪花状结构,其中相对的2个金属圆柱、2组压电陶瓷晶堆和中心正六棱柱金属块构成一个半波长夹心式压电激励源,因此换能器整体可以看作是3个半波长夹心式压电激励源耦合形成雪花形结构。当3个方向的半波长夹心式压电激励源同时纵向共振时,雪花形换能器整体做纵向耦合共振,由此实现声波沿着换能器的6个金属盖板向外辐射。

图1 雪花形夹心式压电换能器的结构示意图和试验样品Fig.1 The structure diagram and experimental sample of snowflake sandwich piezoelectric transducer

1.2 等效电路及共振频率方程

由以上分析可知,雪花形压电换能器做纵向耦合共振时,其振动可分解为6组压电陶瓷晶堆和金属圆柱的一维纵向振动与中心正六棱柱金属块3个方向的纵向耦合振动。由机电类比原理可知,金属圆柱的纵向振动可由T形等效网络[21-23]表示,压电陶瓷晶堆的纵向振动可由梅森等效电路[24]表示,而中心正六棱柱金属块纵向耦合振动的等效电路需要根据耦合振动理论和力电类比原理重新构建,这部分工作也是本文的理论创新所在。

1.3 中心六棱柱形耦合块等效电路模型构建

如图2所示,正六棱柱金属块的高度和边长均为H。当正六棱柱金属块做3个方向的纵向耦合振动时,忽略剪切和扭转振动,即只考虑纵向振动时,由耦合振动理论可知正六棱柱金属块的应力和应变满足关系为[25]

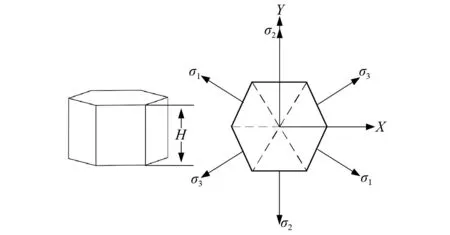
图2 正六棱柱金属块的几何结构及受力示意图Fig.2 The geometric structure and force diagram of thehexagonal prism metal block

(1)

(2)

(3)

式中:εx,εy,εz和σx,σy,σz分别为各方向上的应变和应力;E和v分别为材料的弹性模量和泊松比。由于正六棱柱金属块z方向上的尺寸小于x和y方向纵波波长的四分之一,金属块纵向耦合振动时,z方向的等效应变几乎为零,令εz=0,方程式(3)简化为

σz=v(σx+σy)

(4)

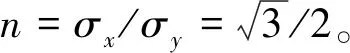
(5)

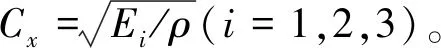
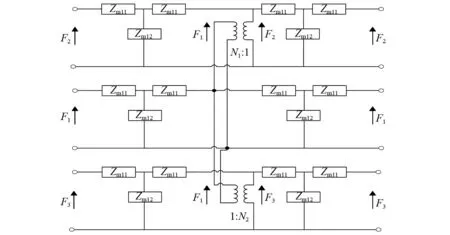
图3 正六棱柱金属块纵向耦合振动的机电等效电路图Fig.3 Electromechanical equivalent circuit diagram of longitudinal coupling vibration of the hexagonal prism metal block

建立了正六棱柱金属块纵向耦合振动的等效电路模型后,对于外部压电陶瓷晶堆和金属盖板的纵振分别用梅森等效电路及T形等效网络表示,各组成部分满足机械上串联、电学上并联的边界条件,结合图3可得如图4所示的雪花形夹心式压电换能器纵向耦合振动的整体等效电路。图4中区域1-3分别表示正六棱柱金属块、压电陶瓷晶堆和金属盖板的等效电路。

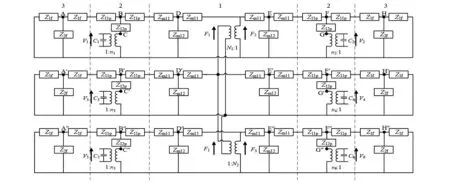
图4 雪花形夹心式压电换能器纵向耦合振动等效电路图(一)Fig.3 Equivalent circuit diagram of longitudinal coupling vibration of the snowflake sandwich piezoelectric transducer (I)

由雪花形夹心式压电超声换能器的结构及工作原理和图4所示的等效电路可知,换能器的六个输入端在电学上并联,并且每个输入支路呈对称结构,易知在点A、A′与A″,B、B′与B″,C、C′与C″,D、D′与D″,E、E′与E″,F、F′与F″,G、G′与G″,H、H′与H″上的电位相等,根据串并联欧姆定律,图4所示的换能器的等效电路可简化如图5所示。由于换能器6个支路的电路参数完全相同,图5中,新的串并联阻抗均变为原来相应位置阻抗的三分之一。

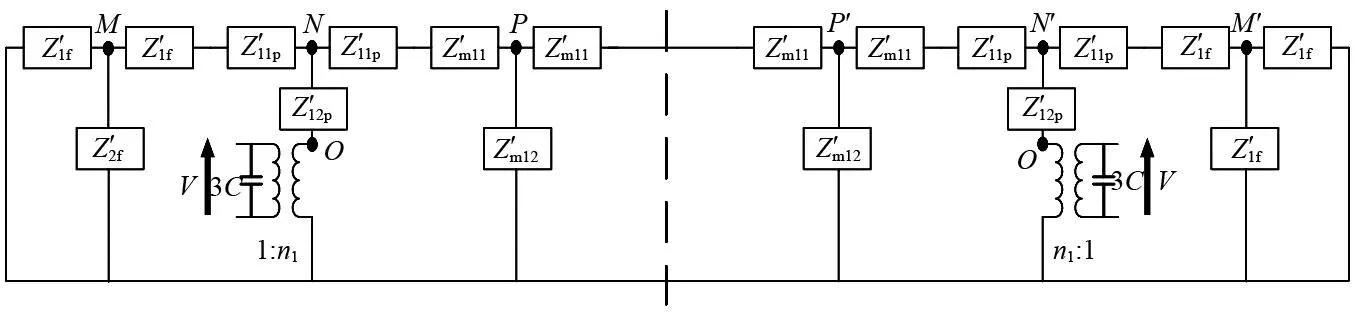
图5 雪花形夹心式压电换能器纵向耦合振动等效电路图(二)Fig.5 Equivalent circuit diagram of longitudinal coupling vibration of the snowflake sandwich piezoelectric transducer (Ⅱ)

电路中等电位点之间可将对应阻抗视为并联,图5所示等效电路由于其对称性,存在M与M′、N与N′、O与O′、P与P′的电位相等,且雪花形换能器纵向耦合振动时位移节点处于正六棱柱金属块的几何中心,根据串并联欧姆定律和力电类比原理可将图5所示的等效电路进一步简化,如图6所示。图6中各参数的表达式

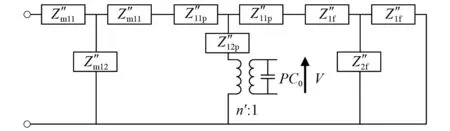
图6 雪花形夹心式压电换能器纵向耦合振动等效电路图(三)Fig.6 Equivalent circuit diagram of longitudinal coupling vibration of the snowflake sandwich piezoelectric transducer (Ⅲ)

由图6可知,基于传输线阻抗变换得到雪花形夹心式压电超声换能器的输入机械阻抗Z0为

(6)

(7)

(8)

式中,Zb和Zc为计算过程中的传输变量,据此可得雪花形夹心式压电超声换能器的输入机电阻抗为

(9)

令换能器输入机电阻抗中抗分量为零,得到其共振频率方程为

Im(Ze)=0

(10)

令换能器输入机电阻抗中抗分量为无穷大,得到其反共振频率方程为

Im(Ze)=∞

(11)

2 理论分析及结果验证

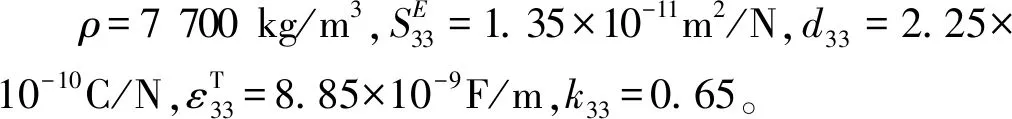
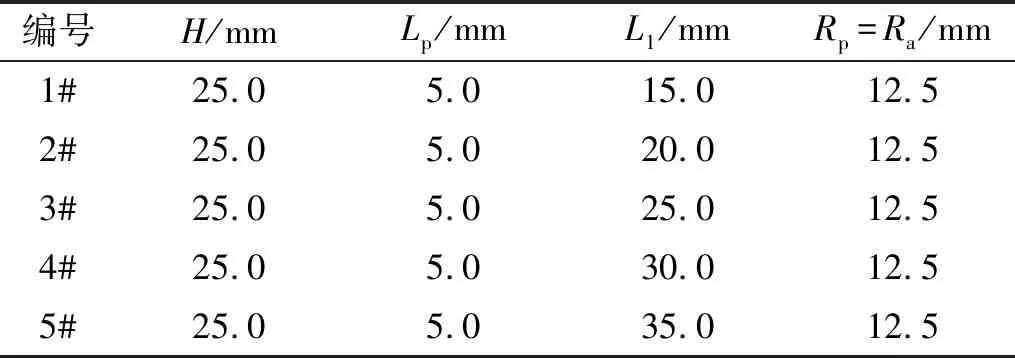
表1 雪花形夹心式超声换能器的尺寸参数

表2 雪花形夹心式压电超声换能器的材料参数

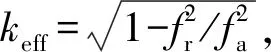
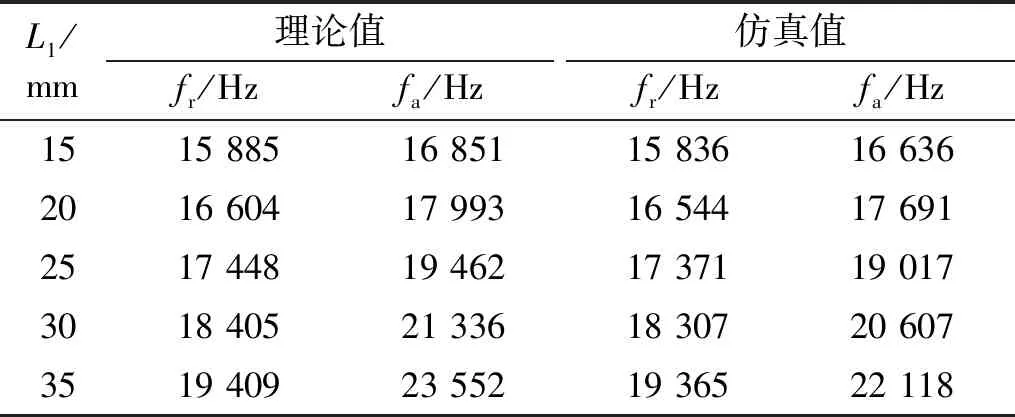
表3 压电陶瓷晶堆位置对换能器纵向耦合共振频率及反共振频率的影响

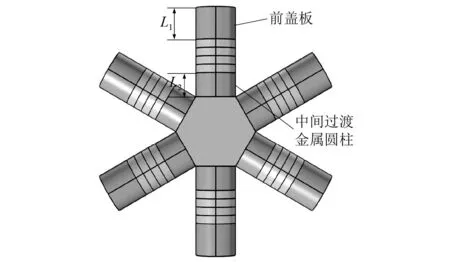
图7 雪花形换能器结构示意图Fig.7 Structure diagram of the snowflake transducer

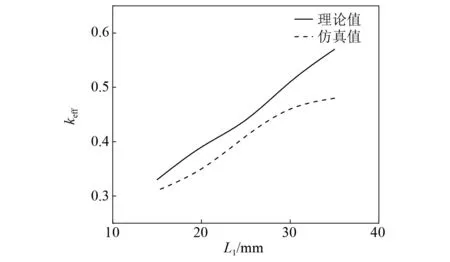
图8 换能器有效机电耦合系数随压电陶瓷晶堆位置变化曲线Fig.8 The effective electromechanical coupling coefficient of transducer varies with the position of piezoelectric ceramic stack

由表4可知,随着换能器纵向尺寸的增加,共振频率减小。等效电路法计算的换能器纵向耦合共振频率与有限元仿真得到的频率值非常接近,试验测量的换能器共振频率小于理论计算和有限元仿真值,理论计算与试验测试的共振频率相对误差为7.6%。图9为5#换能器通过等效电路法、有限元仿真及试验测量得到的阻抗频响曲线,阻抗最小处对应于换能器的纵向耦合振动模态,试验测试装置如图8所示,相应的频率值至见表3,三种方法所得结果基本一致。理论计算和有限元仿真结果与试验测量结果存在一定范围内的合理偏差,其主要原因是:首先,理论计算所用的标准材料参数与实际的材料参数或多或少存在差异;其次,在分析中认为换能器的纵向耦合振动是由三个方向的一维纵向振动复合而成,忽略了由泊松效应在z方向产生的弱横向耦合振动;最后,换能器试验样品通过预应力螺栓对每组压电陶瓷晶堆施加了一定的预应力,同时在压电陶瓷晶片之间设置有电极片,理论计算时忽略预应力和电极片的影响、将压电陶瓷圆环近似为压电陶瓷圆片,理论计算模型的简化近似处理必然会产生理论计算结果与试验测试结果之间的偏差。

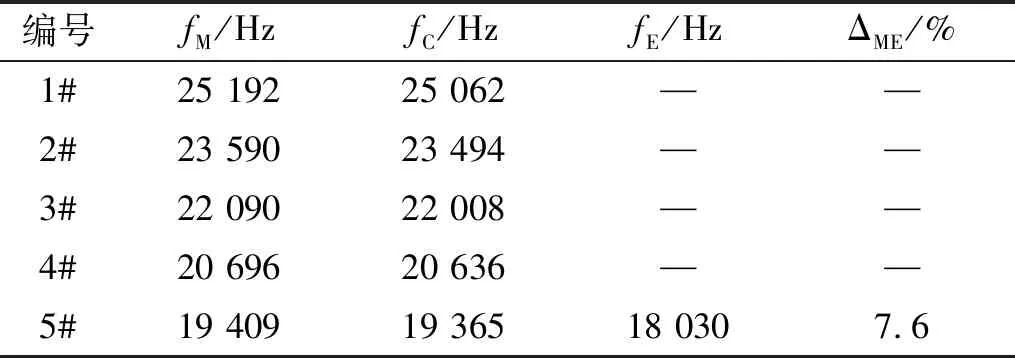
表4 换能器的纵向耦合共振频率及相对误差

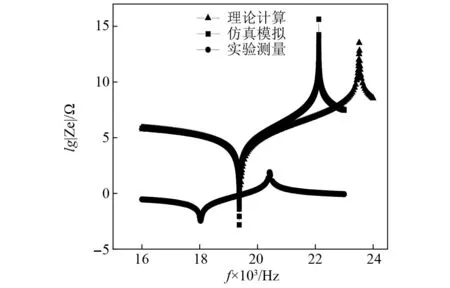
图9 换能器阻抗频响曲线Fig.9 Impedance frequency response curve of transducer

图10 换能器的共振频率测试装置Fig.10 Resonance frequency test device of transducer

图11为有限元软件仿真所得雪花形夹心式超声换能器在共振频率为19 365 Hz时的模态振型图。图12为有限元软件仿真所得到的在一阶纵向耦合振动频率下雪花形换能器沿2方向的轴向位移振幅分布曲线,换能器纵向耦合振动时1、2、3方向沿轴向的位移振幅完全一致,每个方向均为一个半波长振子,3个半波长振子的一阶纵向振动复合形成雪花形换能器的一阶纵向耦合振动。由图11和图12可知,雪花形夹心式超声换能器的纵向耦合振动由1、2、3方向的3个半波长纵向压电振子耦合而成,6个输出端具有相同的振动相位和位移振幅输出,由此实现了换能器的二维六向超声辐射。

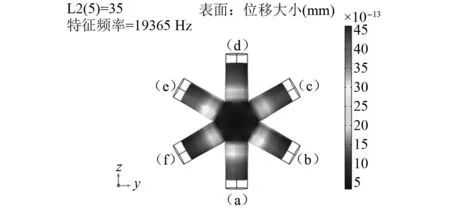
图11 换能器模态振型图Fig.11 Modal figure of transducer

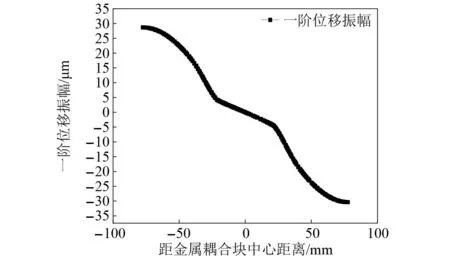
图12 换能器2方向的轴向位移振幅分布曲线Fig.12 Axial displacement amplitude distribution curve of transducer in 2 directions

为了测试换能器在纵向耦合共振模式下6个输出端的位移振幅,通过AG-1024超声功放激发换能器纵向耦合共振,同时用LV-S01激光测振仪对换能器的6个输出端的位移振幅进行测试,试验测试装置如图13所示。换能器的位移振幅测试结果如图14所示。图14(a)～(f)分别对应于图11所示的换能器的6个端面的位移振幅测试结果。由图14可知,在纵向耦合共振模式下换能器的6个输出端的位移振幅介于5.5～6.9 μm之间。理想的情况下换能器的6个输出端的位移振幅应该完全相同,然而,在实际的加工组装过程中很难保证6个方向的压电晶片的性能、金属圆柱体的加工尺寸、装配时施加的预应力完全一致,由此产生6个方向的位移振幅存在一定范围内的偏差。由此表明,通过雪花形的结构设计和纵向振动模式耦合有效实现了单个换能器的二维六向超声辐射,改善了传统的一维纵向振动夹心式压电超声换能器的超声辐射方向单一和超声辐射面积小的不足。该换能器有望作为一种多头辐射超声换能器应用于多向超声焊接或多向超声辐射领域。

图13 换能器的位移振幅测试装置Fig.13 Displacement amplitude test device of transducer

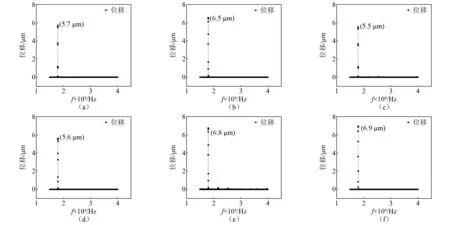
图14 换能器纵向耦合共振时6个输出端的位移振幅Fig.14 Displacement amplitude of six output ends of transducer in longitudinal coupling resonance

3 结 论

本文提出了一种新型的雪花形夹心式压电超声换能器,基于耦合振动理论和机电类比原理,建立了换能器的等效电路模型及共振频率方程,分析了金属盖板纵向尺寸对换能器共振频率的影响及纵向尺寸一定时压电陶瓷晶堆位置对换能器有效机电耦合系数的影响,加工了相应换能器试验样品,对换能器的共振频率和6个输出端的位移振幅进行了测试。结论如下:

(1)建立的雪花形换能器纵向耦合振动的等效电路模型,可实现对该类换能器的共振频率、有效机电耦合系数、机电阻抗特性等关键性能参数计算分析,解决了该类换能器的简明工程理论设计问题。

(2)雪花形换能器金属前盖板的纵向尺寸增大,换能器的纵向耦合共振频率逐渐减小;压电陶瓷晶堆两端的金属圆柱(前盖板L1和过渡金属圆柱L2)纵向尺寸一定时,压电陶瓷晶堆越靠近中心正六棱柱形金属块,换能器的有效机电耦合系数越大,有着更高的机电转换效率。

(3)雪花形换能器在纵向耦合共振模式下工作时,6个输出端具有基本一致的纵向位移振幅和相同的振动相位。该振动模式既具有夹心式压电超声换能器结构简单、性能可靠的优点,又克服了传统的纵向振动夹心式压电换能器一维超声辐射的不足,实现了单个换能器多方向超声辐射的特点,有望应用于多维超声加工、多向超声辐射等领域中。