地震波斜入射下水平成层覆盖层地基波动输入研究
王 飞, 宋志强, 刘云贺, 李 闯, 李正贵, 胡安奎, 田 庆
(1. 西华大学 能源与动力工程学院,成都 610039; 2. 西安理工大学 省部共建西北旱区生态水利国家重点实验室,西安 710048;3. 陕西铁路工程职业技术学院, 陕西 渭南 714099)
随着坝工技术进一步提高,传统水电开发逐步向覆盖层普遍发育的西南河流上转移。西南河流河床覆盖层深厚,其厚度达数十米甚至上百米,其中某拟建水电工程坝址覆盖层最大厚度甚至超过500 m[1-2],属超深厚覆盖层工程。同时,西南地区强震频发,地震作用下覆盖层土体表现明显非线性特性[3],覆盖层上大坝抗震安全面临严峻挑战。地震动输入是覆盖层上大坝地震响应分析和安全评价的基础,目前覆盖层地基地震动输入大多采用固定边界结合一致地震动的方法[4-5],即无质量地基输入模型[6]。无质量地基模型中大坝引起的外行散射波无法向远域逸散,导致大坝地震响应被高估[7-8],同时无法考虑土体动力非线性造成的截断边界上输入地震荷载的非一致性,该模型难以合理模拟覆盖层地基地震动输入。
刘晶波等[9]提出的波动输入方法解决了均质弹性半空间介质辐射阻尼效应问题,该方法包括地基截断边界上施加的黏弹性边界和由自由场转化而来的等效结点荷载,计算精度高,被广泛应用于基岩上大坝地震响应分析[10-12]。覆盖层土体动力非线性和成层特性,引起不同深度自由场和黏弹性边界参数在时间和空间上呈现非线性变化,极大增加了覆盖层地基自由场和黏弹性边界参数求解难度。杨正权等[13-14]在覆盖层地基地震动输入中引入黏弹性人工边界,采用等效线性化方法反映黏弹性边界参数随人工边界内侧土体动剪应变变化,提高了黏弹性边界吸能效果,但没解决覆盖层地基人工边界上输入荷载的问题。Zou等[15-16]建立了人工边界参数随覆盖层截断边界内侧土体动剪应变变化的等效人工边界单元,利用剪切箱模型[17]数值求解了地震波垂直入射下覆盖层场地自由场,合理解决了地震波垂直入射下覆盖层地基地震动输入问题。剪切箱模型适用于相同高程运动一致的情况,地震波斜入射下覆盖层相同高程土体运动具有空间非一致性[18],剪切模型不能应用求解地震波斜入射下覆盖层自由场。
刘晶波等[19]提出了平面波斜入射下弹性水平成层半空间自由场一维化有限元时域计算法,该方法无法根据平坦基岩或覆盖层表面地震波记录反演水平成层半空间自由场,同时也未见该方法在覆盖层地基自由场计算方面的应用。通常平坦基岩或覆盖层表面地震动容易被获得,基岩或土层中地震动难以得到[20]。大多数情况下需要根据地表地震动反演覆盖层自由场。
本文引入势函数理论[21],建立覆盖层顶层波幅矩阵与任意层波幅矩阵之间的动态传递关系,由基岩面入射波和地表面地震动分别正演和反演水平成层覆盖层地基应变分量;采用等效线性化方法[22]反映土体动力非线性特性,结合二维平面应变理论获得水平成层非线性覆盖层地基自由场解析解,进而转换为地震输入荷载。远域覆盖层采用Wang等研究中建立的等效黏弹性人工边界单元模拟,边界单元参数随土体动剪应变动态实时变化,建立了适用于地震波斜入射下水平成层覆盖层地基地震动输入方法。通过两个数值算例验证了本文方法的合理性。
1 水平成层覆盖层自由场解析计算
1.1 弹性水平成层覆盖层
图1中弹性水平成层覆盖层由n层土层组成,第i层Lame常数、剪切模量和密度分别为λi、Gi和ρi,土层厚度为hi。
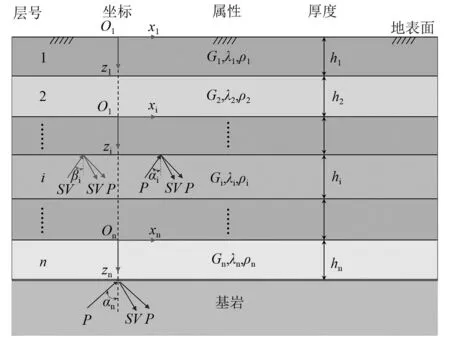
图1 地震波斜入射下成层覆盖层地基分析模型Fig.1 Analysis model of foundation with layered overburden under seismic wave oblique incidence
土体位移运动如式(1)所示
u=∇φ+∇ψ
(1)
式中:φ为P波标量势;ψ为SV波矢量势。
基于势的波动方程为
(2)
式中:∇2为拉普拉斯算子;cP和cS分别为P波和SV波波速。
第i层中,满足方程式(2)的势函数为
(3)
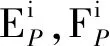
第i层x方向和z方向位移可由势函数表示为[24]
(4)
第i层应力表示为
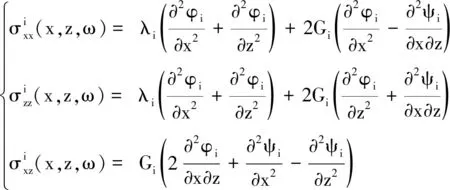
将式(3)分别代入式(4)和式(5),得到
(6)
式中:Qi为第i层系数矩阵;Ei为第i层幅值矩阵;Ui为第i层指数矩阵。
相邻土层分层面满足位移和应力连续条件为
(7)
将式(7)代入式(6),可得到
Ei+1=(Qi+1)-1QidiEi
(8)
式中:
根据式(8)可建立第n层幅值矩阵与第1层幅值矩阵之间的传递关系
(9)
式中,Kn-1,1为第n层和第1层之间的幅值传递矩阵。
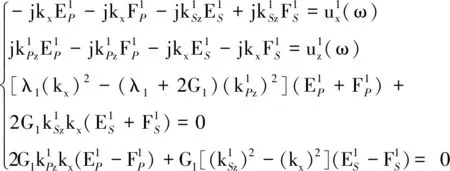
由式(10)求解最顶层幅值矩阵E1,根据式(9)中传递关系依次求解每一层幅值矩阵,通过式(6)经傅里叶逆变换获得土体时域应变分量,也可以获得位移和应力等物理量。上述过程为基于地表地震动直接反演这个覆盖层地基线性自由场,避免了先反演覆盖层底部地震动,再根据底部地震动正演整个覆盖层自由场等步骤。
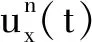
P波入射
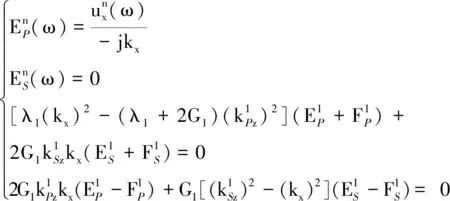
SV波入射
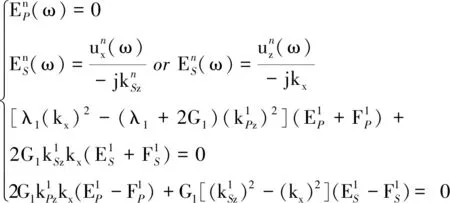
求解顶层幅值矩阵E1,然后按照前述过程求解每一层土体时域应变分量。
1.2 非线性水平成层覆盖层
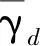
(13)
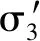
由二维平面应变状态理论[29],关系为
(14)
式中:ε1和ε3分别为大、小主应变;εxx,εzz和γxz分别为x向、z向正应变和剪应变,由位移-应变关系可得
(15)
1.3 非线性水平成层覆盖层自由场解析计算流程
步骤1依据实际地质资料建立水平成层覆盖层地基有限元模型,赋予不同土层相应静力材料参数,计算得到覆盖层土体单元静力初始围压;
步骤2将土体动力材料参数和初始围压代式(13)计算土体最大动剪切模量,以此作为初始计算参数,同时依据沿深度方向土体最大动剪切模量Gmax分布情况对土层进行细分,即单元最大动剪切模量相近的划分为一小层;
步骤3对地表地震动或建基面入射波进行傅里叶变换(fast Fourier transform,FFT),根据式(10)或式(11)求解最顶层幅值矩阵E1,通过传递矩阵获得第i层幅值矩阵Ei,经傅里叶逆变换(inverse fast Fourier transform,IFFT)获得土体时域应变分量,利用式(13)计算不同深度处单元归一化动剪应变;
步骤4将归一化动剪应变继续代入等价黏弹性模型中,确定新的等效动剪切模量和等效阻尼比,按照步骤3重新求解每一小层土体归一化剪应变,以归一化剪应变为迭代收敛指标,若本次计算值与上一次计算值的误差满足允许值,则迭代收敛,否则继续迭代,直至迭代满足允许值;
步骤5将满足迭代收敛的等效动剪切模量和等效阻尼比作为水平成层覆盖层自由场最终动力计算参数,按照步骤3获得地震波斜入射下水平成层覆盖层自由场非线性时域解析解。
2 地震波动输入方法
地震波斜入射下非线性水平成层覆盖层地基波动输入方法包括:自由场计算、动力人工边界参数计算和等效输入荷载计算。自由场计算过程按照1.3节,动力人工边界参数计算方法见2.1节,等效输入荷载由自由场和边界参数综合而得,计算方法见2.2节。
2.1 非线性黏弹性人工边界单元
Wang等研究中建立了黏弹性人工边界单元,黏弹性人工边界单元实现方法:在已有有限元模型外法向延伸一层有限单元,将外层有限单元外侧固定,通过给外层有限单元赋予等效材料参数使其作用等价于集中黏弹性人工边界。黏弹性人工边界单元参数依附于邻近内层单元,通过等效线性化方法,黏弹性人工边界单元参数随邻近内层单元动剪应变非线性变化,提高黏弹性人工边界单元吸能能力。非线性黏弹性人工边界单元有较高计算精度,与远置边界计算结果相比,最大误差在5%左右。
黏弹性人工边界单元等效剪切模量、等效弹性模量和等效泊松比如式(16)、式(17)和式(18)所示
(16)
(17)
(18)
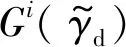
采用与刚度成正比的阻尼集成黏弹性边界单元阻尼矩阵,阻尼系数按式(19)取值
(19)
图2为依附于内层土体单元的黏弹性人工边界单元,非线性黏弹性人工边界单元实现流程为:
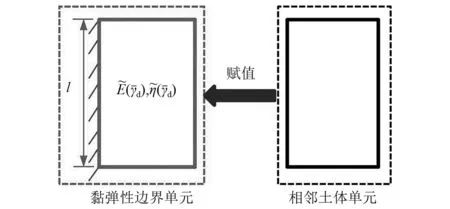
图2 黏弹性边界单元Fig.2 Viscoelastic artificial boundary element
步骤1每次计算前,由单元震前围压、土体动力参数和上次计算过程中最大动剪应变确定单元动剪切模量;
步骤2搜索与黏弹性人工边界单元相同高程且相邻的土体单元,根据式(17)、式(18)和式(19)和相邻单元动剪切模量,确定等效弹性模量、等效泊松比和平均刚度比例阻尼系数,赋给对应黏弹性人工边界单元;
步骤3进行下次计算,获得地震过程中新的最大动剪应变;
步骤4重复步骤1~步骤3,直至满足迭代收敛标准,得到最优的人工边界单元等效参数。
2.2 等效输入荷载
第2节解析计算了地震波斜入射下非线性水平成层覆盖层地基自由场,覆盖层地基截断边界处自由场转化为边界单元上等效输入荷载,实现地震动波动输入。与等效黏弹性人工边界单元匹配的等效输入荷载如式(20)所示[30]
(20)
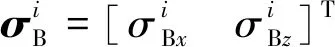
边界法向
(21)
边界切向
(22)
在ABAQUS有限元软件中,在等效黏弹性边界单元与内层土体单元相交面切向和法向施加均布荷载。
2.3 地震波动输入流程
地震波斜入射非线性覆盖层地基波动输入流程图,如图3所示。
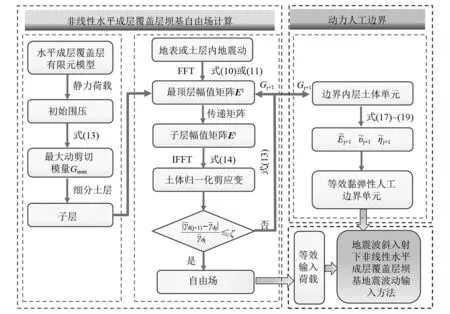
图3 地震波斜入射非线性覆盖层地基波动输入流程图Fig.3 Wave input process of foundation with nonlinear overburden under seismic wave oblique incidence
3 水平成层覆盖层地基波动输入数值验证
以图4中弹性水平双层覆盖层为研究对象,土层厚度均为25 m,水平向跨度为100 m,在ABAQUS有限元软件中采用四结点双线性平面应变四边形单元CPE4对覆盖层进行离散,单元尺寸为1.0 m,表1为弹性水平成层覆盖层材料参数。依据B点入射波和地表面O点地震动分别正演和反演覆盖层底部和侧边界自由场,B点入射波位移时程为图5中位移时程,地表面O点水平和竖向地震动位移时程分别为图6中位移时程,采用等效黏弹性人工边界单元模拟远域覆盖层辐射阻尼效应和,将自由场转化为等效黏弹性人工边界单元表面上输入荷载,分析波动输入下地表中心A点位移和中部应力沿深度变化,并与解析解对比。依据B点入射波正演自由场时,P波入射角为30°;依据点O地震动反演自由场时,顶部土层上行P波入射角为30°,顶层土层内下行P波反射角,上行SV波和下行SV波入射角和反射角由Snell定律确定,下行P波反射角为30°,上行和下行SV波入射角和反射角均为16.54°。图7给出了上行P波、下行P波、上行SV波以及下行SV波引起的水平向和竖向位移时程。

表1 弹性水平双层覆盖层力学参数
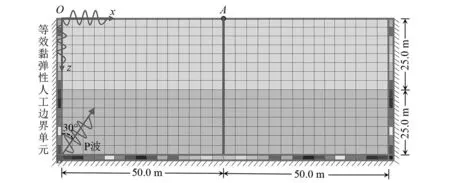
图4 弹性水平双层覆盖层Fig.4 Elastic horizontal double-layers overburden
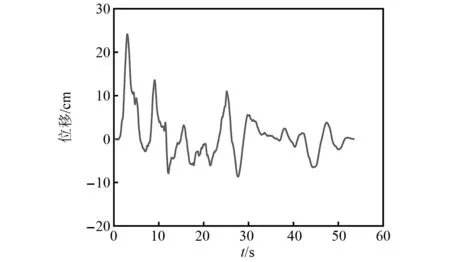
图5 正演自由场时B点入射波位移时程Fig.5 Displacement time history of the incident wave at point B under forward modeling the free field
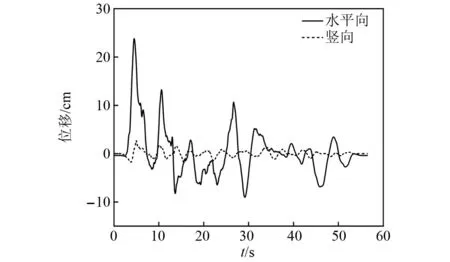
图6 反演自由场控制点O设计地震动位移时程Fig.6 Displacement time histories of design ground motion at control point O under inverting the free field
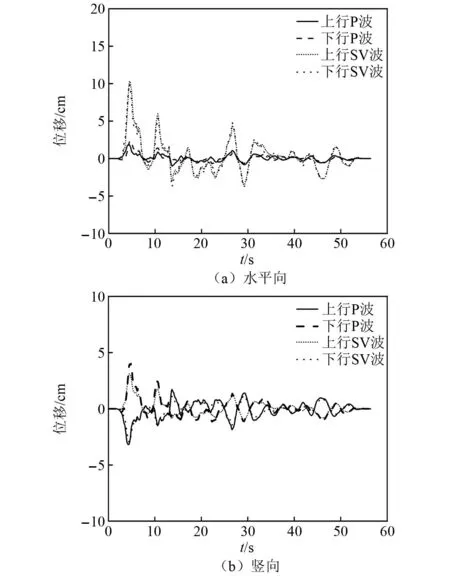
图7 上行和下行P波以及上行和下行SV波引起的水平向和竖向位移时程Fig.7 Horizontal and vertical displacement time histories caused by the incident and reflected P-waves, as well as the incident and reflected SV-waves
图8为依据B点入射波正演覆盖层边界自由场波动输入下表面中心点A位移时程和中部应力峰值沿深度的分布。图9为依据地表面点O地震动反演覆盖层边界自由场波动输入下表面中心点A位移时程和中部应力峰值沿深度的分布。
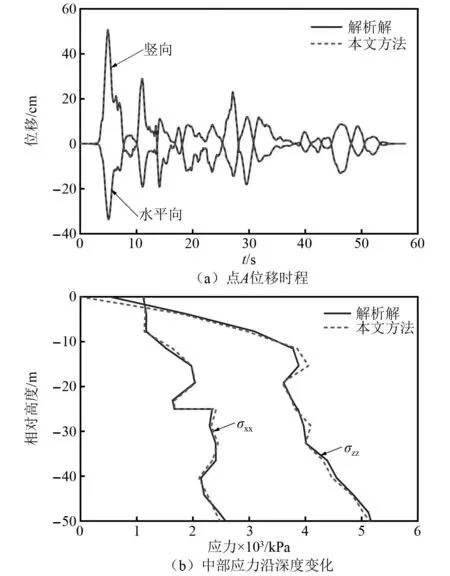
图8 正演波动输入下弹性水平成层覆盖层自由场Fig.8 Elastic horizontal layered overburden free field under forward wave input
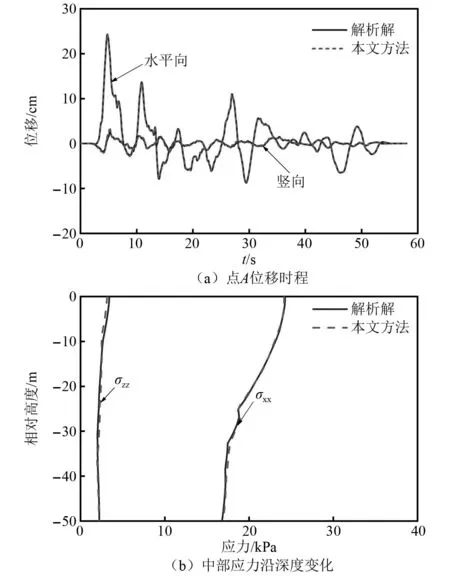
图9 反演波动输入下弹性水平成层覆盖层自由场Fig.9 Elastic horizontal layered overburden free field under inversion wave input
图8和图9表明,地表面中心点A位移时程和中部应力响应均与解析解拟合良好,证明了本文建立的波动输入方法即适用于依据深部基岩中入射波求解地震波斜入射下弹性水平成层覆盖层地震响应,也适用于依据地表地震动求解地震波斜入射下弹性水平成层覆盖层地震响应,并且计算精度较高。
以某拟建水电工程坝址河床覆盖层为原型。根据地质资料,地表以下300 m深度范围内,覆盖层近似水平成层,这里覆盖层深度取为240 m。如图10所示,覆盖层自上而下分为4个土层,第①层为砂卵石层,厚20 m,第②层为含砾中砂层,厚70 m,第③层为粉质黏土层,厚20 m,第④层为粗砂土,厚130 m。首先对覆盖层地基进行静力非线性弹性计算,土体应力-应变关系采用邓肯-张E-v模型模拟,静力计算参数如表2所示,获取单元震前初始围压。土体动力计算采用等价黏弹性模型,动力计算参数如表3所示。依据震前初始围压和动力计算参数确定土体最大动剪切模量,对覆盖层土层进一步细分,分成33个小层。
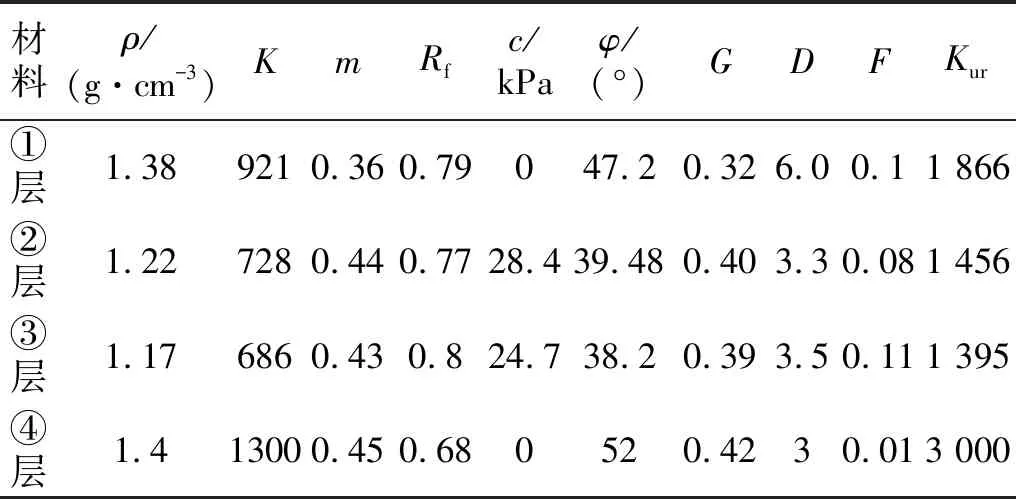
表2 覆盖层静力计算参数Tab.2 Static calculation parameters of overburden layers
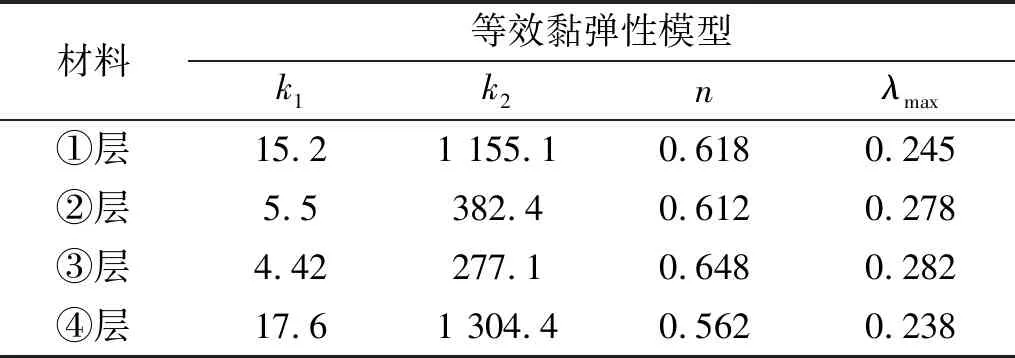
表3 覆盖层动力计算参数Tab.3 Dynamic calculation parameters of overburden layers
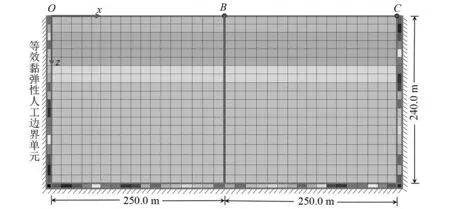
图10 非线性水平成层覆盖层地基Fig.10 Foundation with horizontal layered overburden
为了与该工程场地设计地震动峰值加速度0.53g匹配,将图6中水平向和竖向地震动幅值分别按2.65倍和1.71倍调幅,获得深部B点入射波(取水平向地震动)和覆盖层地表面控制点O地震动时程。依据B点入射波正演自由场时,P波入射角为10°;依据点O地震动反演自由场时,顶部土层上行P波入射角为10°,其余各波型入射角或反射角由Snell定律确定。
图11和图12分别为正演和反演非线性水平成层覆盖层自由场的波动输入下中部位移峰值和应力峰值沿深度变化。图11和图12均表明,中部位移峰值和应力峰值与解析解拟合良好,计算误差在5%以内,计算精度较高。
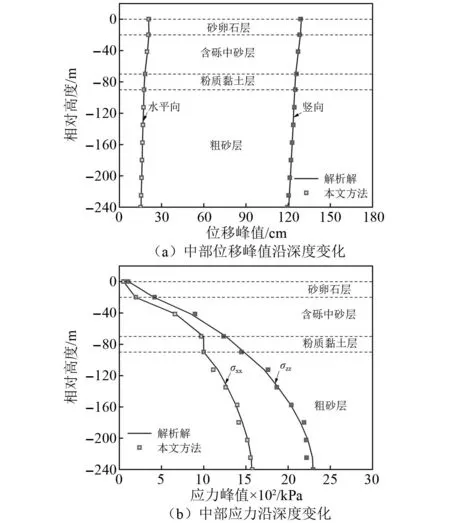
图11 正演波动输入下非线性水平成层覆盖层自由场Fig.11 Nonlinear horizontal layered overburden free field under forward wave input
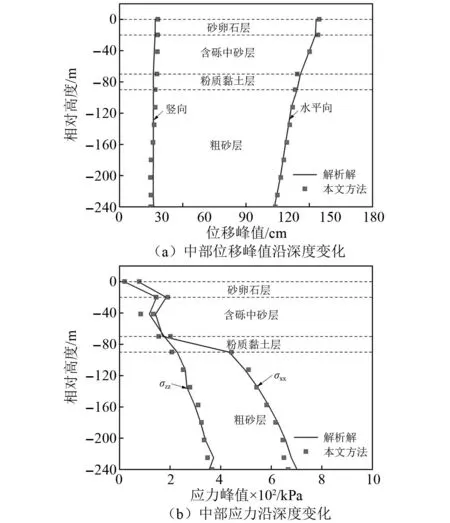
图12 反演波动输入下非线性水平成层覆盖层自由场Fig.12 Nonlinear horizontal layered overburden free field under inversion wave input
本文建立的波动输入方法适用于依据地基深部入射波计算地震波斜入射下非线性水平成层覆盖层地震响应,也适用于依据地表地震动计算地震波斜入射性非线性成层覆盖层地震响应,合理解决了地震波斜入射下水平成层覆盖层地基地震动输入问题。
4 结 论
地震作用下覆盖层土体表现明显的非线性行为,无质量地基模型和通常用于线弹性岩基的波动输入方法难以应用于地震波斜入射下非线性水平成层覆盖层地基。为合理解决地震波斜入射下非线性水平成层覆盖层地基地震动输入问题,本文主要工作和结论如下:
(1)建立了地震波斜入射下非线性水平成层覆盖层地基自由场解析计算方法。以水平成层覆盖层地基为研究对象,基于势函数理论,建立了覆盖层顶层波幅矩阵与任意层波幅矩阵之间的动态传递关系,得到任意层幅值矩阵,通过傅里叶逆变换求解了弹性水平成层覆盖层地基应变时域分量;基于二维平面应变状态理论和等效线性化方法,迭代计算了地震波斜入射下非线性水平成层覆盖层地基自由场时域解析解;该方法不仅能够依据覆盖层深部斜入射波正演覆盖层地基自由场,还能够依据地表面地震动反演覆盖层地基自由场,具有避免再根据地基底部地震动正演自由场等过程的优点。
(2)建立了适用于地震波斜入射下非线性水平成层覆盖层地基地震波动输入方法。利用作者前期发展的边界参数随边界内层土体单元动剪应变动态实时变化的非线性黏弹性人工边界单元(发挥人工边界最优吸能效果),结合由自由场转换而来的等效输入荷载,实现了地震波斜入射下非线性水平成层覆盖层地基地震波动输入。研究了覆盖层深部斜入射波和地表地震动已知的两种情况下弹性水平双层和非线性水平多层覆盖层地基地震响应,计算结果均表明,覆盖层地基位移和应力均与解析解拟合良好,验证了本文建立的波动输入方法的高精度性,为地震波斜入射下水平成层覆盖层地基上土石坝地震响应分析提供基础。

