新型双重自复位摩擦阻尼器试验及数值模拟

屈俊童, 白宇翔, 张 超, 李昱衡, 王文彬, 浦钧翔

(云南大学 建筑与规划学院,昆明 650504)

通过在结构中设置耗能装置,消能减震技术减轻了地震对结构的破坏,当前工程中常用的阻尼器主要有液体黏滞阻尼器、金属屈服型阻尼器、屈曲约束支撑及摩擦阻尼器等[1]。但这些阻尼器并不具备自复位功能,强震作用后存在较大的震后残余变形,可能造成减震结构的残余变形过大,不利于阻尼器及结构的震后恢复[2]。对此,国内外学者通过在耗能装置中增加自复位组件提出了大量自复位阻尼器。

现阶段对自复位阻尼器的研究主要采用高强预应力筋、碟簧及形状记忆合金(shape memory alloy, SMA)提供复位驱动力,从而减小阻尼器卸载后的残余变形。Christopoulos等[3-4]采用高强预应力筋作为阻尼器复位组件,提出了具备“旗帜型”滞回曲线的自复位耗能支撑。Xu等[5-6]通过预压碟簧驱动阻尼器复位提出了新型自复位耗能支撑,并进行低周往复加载试验。严鑫等[7]将预压碟簧与黏滞阻尼器并联,提出了自复位黏滞阻尼器。SMA同时具备良好的超弹性及高阻尼特性,卸载后可恢复至初始形状,是制作自复位阻尼器的理想材料[8]。Shi等[9]将SMA绞线同时用作耗能及自复位模块,研发了新型SMA自复位支撑,分析了自复位支撑参数对钢框架结构抗震性能的影响。Wang等[10]在铅芯叠层橡胶隔震支座中双向设置U型SMA阻尼器,提出了可减小隔震层残余变形的新型自复位隔震支座。

摩擦阻尼器具备出力稳定、耗能性能良好及造价低廉等优点,以摩擦阻尼器作为耗能组件的自复位阻尼器研究备受关注。张艳霞等[11]基于预应力钢绞线和传统摩擦阻尼器发展了自复位免修复摩擦耗能支撑,并进行缩尺试件的拟静力试验和数值模拟。任文杰等[12]将压缩圆柱螺旋弹簧与斜面变摩擦耗能装置并联,提出了自复位变摩擦阻尼器并进行拟静力试验。邱灿星等[13-14]采用SMA螺栓对滑动摩擦提供压应力,研发了自复位摩擦阻尼器,通过试验验证理论公式及数值模拟的准确性。

综上所述,目前的自复位阻尼器采用了高强预应力筋、碟簧及SMA等复位驱动方式中的一种,但单一的复位驱动方式不易于提供与更高的耗能要求相匹配的复位力,如:难以施加较大的预应力,增大SMA用量容易导致经济成本过高等。对此,本文利用螺旋弹簧变形后产生的弹性力和SMA奥氏体相变力共同驱动阻尼器复位,并将复位弹簧、SMA与摩擦阻尼器并联,提出了新型双重自复位摩擦阻尼器;通过试验考察预紧力、加载位移幅值及复位弹簧组件刚度对阻尼器复位性能及耗能性能的影响,并进行了数值模拟。

1 双重自复位摩擦阻尼器构造及工作原理

1.1 阻尼器构造

按功能的不同,可将新型双重自复位摩擦阻尼器划分为复位螺旋弹簧、SMA拉杆及摩擦耗能装置三个部分,通过复位螺旋弹簧及SMA拉杆的超弹性性能实现双重自复位功能。阻尼器整体由中部钢板、石棉摩擦片、含有固定凸块的上下覆板、复位圆柱螺旋弹簧、SMA拉杆,带孔复位牵引杆及M10高强螺栓组成。

双重自复位摩擦阻尼器的构造如图1所示,阻尼器中部钢板及上下覆板两端分别预留一个矩形导向槽口,用于放置复位牵引杆及阻尼器变形的导向,上下覆板左右两侧分别制作三个M10螺栓预留孔,两端导向槽口后各有一个固定凸块,用于安装复位弹簧。采用环氧树脂在中部钢板上下表面黏接5 mm厚的石棉摩擦片,并将高强螺栓穿过上下覆板施加法向预紧力,从而完成摩擦耗能组件的装配。带孔复位牵引杆穿过阻尼器导向槽口后,阻尼器上下两侧各通过一根直径为4 mm 的超弹性Ni-Ti SMA拉杆及高强螺母将两端的复位牵引杆连接,采用复位螺旋弹簧和高强螺母将各个复位牵引杆与上下覆板处的固定凸块连接,形成双重复位体系。

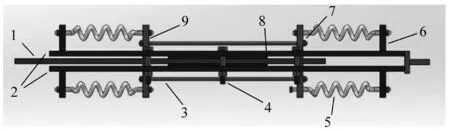
注:1. 中部钢板; 2. 上下覆板;3. SMA拉杆;4. M10高强螺栓; 5.复位螺旋弹簧;6. 固定凸块;7. 高强螺母;8. 石棉摩擦片;9. 复位牵引杆

1.2 阻尼器工作原理

在荷载作用下,阻尼器发生拉伸-压缩变形,SMA拉杆始终保持拉伸状态,而其中一端的复位螺旋弹簧则处于压缩状态。阻尼器通过SMA拉杆的高阻尼特性以及上下覆板与摩擦片间的摩擦来耗散能量。当撤去外荷载后,SMA拉杆的奥氏体相变力与弹簧压缩后的弹性力共同驱动阻尼器复位,产生适配于高耗能要求的复位驱动力,阻尼器工作原理如图2所示。

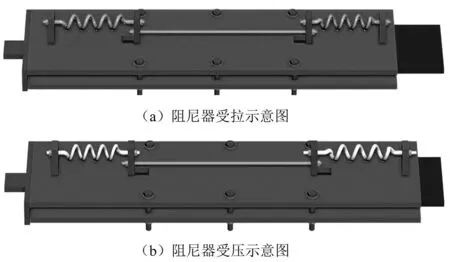
图2 双重自复位摩擦阻尼器工作原理示意图Fig.2 Working principle of dual self-centering friction damper

当拉力超过阻尼器内部摩擦力时,中部钢板与上下覆板发生错动,摩擦片与上下覆板摩擦。以上下覆板为参照,一端的复位牵引杆被中部钢板带动,另一端的则相对静止,进而拉伸SMA拉杆并压缩一端的复位弹簧。同理,阻尼器在受压过程中,摩擦片与上下覆板反向摩擦,一端的复位牵引杆相对于上下覆板静止,另一端则被推动,拉伸SMA拉杆并压缩复位弹簧。其中,复位牵引杆不仅传递了SMA拉力及复位弹性力,对阻尼器的往复运动也起到了导向作用。

2 阻尼器力学性能试验

2.1 试验概况

根据阻尼器构造设计及工作原理加工制作了模型试件, 试件最大行程为21 mm;中部钢板及上下覆板厚度均为10 mm,上下覆板的连接则通过焊接端部连接块实现,各部件尺寸及连接构造如图3所示,尺寸标注单位为毫米;双重自复位体系采用Ni-Ti SMA拉杆(Ni50.1%, Ti49.9%),直径为4 mm,有效长度为300 mm;复位弹簧则采用锰铬合金螺旋弹簧(Mn 1.02%, Cr 0.29%),具体参数如表1所示;摩擦耗能装置预紧力通过扭力扳手施加,石棉摩擦片尺寸为200 mm×140 mm×5 mm,其余构件采用Q235钢。

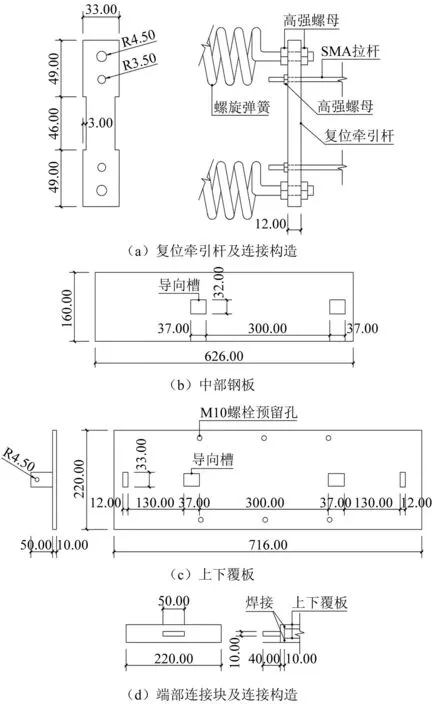
图3 试件主要零件示意图(mm)Fig.3 Main parts of the specimen (mm)

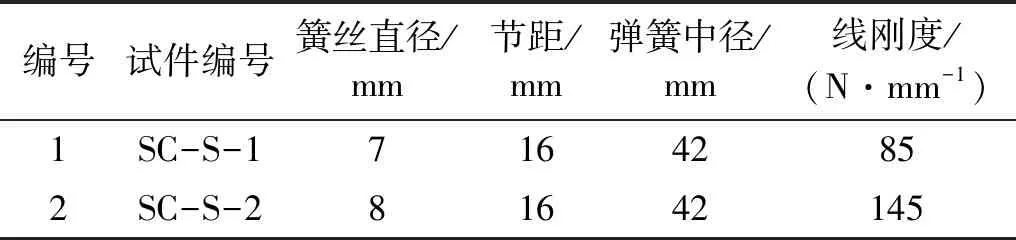
表1 复位弹簧参数Tab.1 Parameters of reset spring

为考察预紧力、加载位移幅值及复位弹簧组件刚度对阻尼器整体复位性能与耗能效果的影响,设计了4组试验,相应的试件则通过阻尼器各功能部件的装配实现;试验采用三级加载位移幅值,各级加载位移幅值分别为9 mm、15 mm和21 mm,共计12个工况,试验工况参数如表2所示。复位弹簧及SMA均未被施加预应力,摩擦耗能装置的预紧力为6个M10高强螺栓的总预紧力。首先,通过昆明理工大学的微机电液伺服万能试验机完成SMA拉杆的20次循环拉伸训练,使SMA性能稳定。采用云南宇州检测技术公司的万能试验机(WAW-100B)对阻尼器进行位移控制滞回加载,试验数据通过控制端计算机自动采集,试验环境温度为15 ℃,试验加载速度均为5 mm/min,试验装置如图4所示。

图4 阻尼器加载试验示意图Fig.4 The schematic of damper loading test

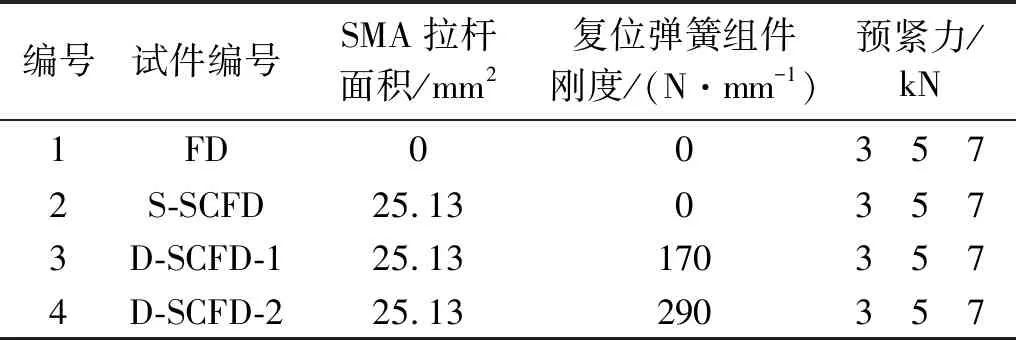
表2 试验工况Tab.2 Test cases

2.2 SMA拉伸训练

SMA应力-应变曲线在等幅循环拉伸训练及变幅拉伸试验中均呈 “旗帜型”,由外荷载引起的塑性变形在卸载后基本恢复,如图5所示。这一现象表明,外力引起了SMA拉杆发生马氏体相变,SMA又在随后的卸载过程中发生了奥氏体相变,SMA具有良好的超弹性性能。

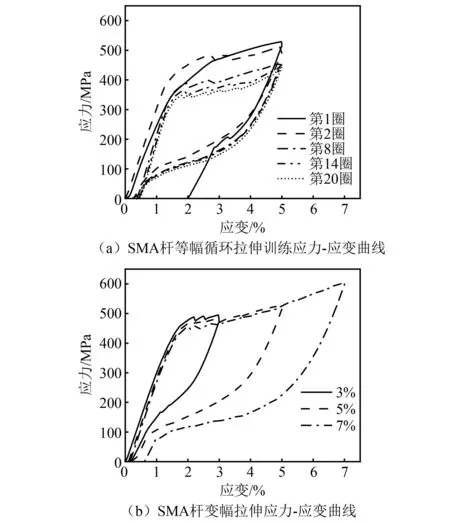
图5 SMA杆应力-应变曲线Fig.5 Stress-strain curves of SMA rod

等幅循环拉伸的加载幅值为5%应变,在第1圈循环拉伸训练中,SMA拉杆卸载后残余应变达到了1.98%,但在后续的拉伸训练中较小;在第8圈拉伸训练后,应力应变曲线趋于稳定。如变幅加载曲线所示,加载至应变1.82%,SMA拉杆开始发生马氏体相变,相变终止于应变6.97%;随加载应变的增大,奥氏体相变起始应变上升,相变终止应变则为0.47%。

SMA相变应力如表3所示,σms、σmf分别为马氏体相变起始应力与相变终止应力,σas、σaf分别为奥氏体相变起始应力与相变终止应力。

表3 SMA杆相变应力Tab.3 Phase transformation stress of SMA rod

2.3 阻尼器试验结果分析

2.3.1 阻尼器力学参数选取

为分析双重自复位摩擦阻尼器的各个力学性能,选用以下参数:

(1) 每周循环加载耗能大小W,量化阻尼器耗能性能,如式(1)所示

W=∬AdA

(1)

式中,A为阻尼器滞回曲线面积。

(2) 割线刚度K,如式(2)所示

(2)

式中:Fmax与Fmin分别为最大与最小阻尼力;Dmax与Dmin分别为最大与最小位移。

(3) 等效黏滞阻尼比ξeq,量化阻尼器阻尼特性,如式(3)所示

(3)

(4) 卸载后残余变形率Rdr,即卸载后残余变形Dr与最大设计行程之比,衡量阻尼器复位性能。

2.3.2 摩擦阻尼器(friction damper,FD)

为获取FD的主要参数,首先进行了FD的力学试验。试件FD在各个工况下的滞回曲线均为矩形,滞回曲线面积随加载位移幅值及预紧力的增大而增大,滞回曲线如图6所示;由于未附加复位驱动装置,FD在卸载后不能复位;根据图6及FD具有两个摩擦面的构造设计可得,FD的滑动摩擦因数为0.50。

图6 FD试验滞回曲线Fig.6 Experimental hysteresis curves of FD

2.3.3 无复位弹簧的SMA-摩擦阻尼器(single self-centering friction damper,S-SCFD)

将SMA与摩擦耗能部件并联后,试件S-SCFD的复位由SMA拉杆驱动,不同试验工况下的滞回曲线形状均为“旗帜型”,如图7所示,相应的力学性能参数如表4所示。由图7可知,刚进入伪屈服状态时的阻尼力存在波动,波动幅值较小,且随着加载位移的增大而减小,阻尼器整体出力较为稳定。随着预紧力的增大,阻尼力及滞回曲线面积增大。最大出力随着加载位移幅值的增大而增大,表明试件S-SCFD具有一定的伪屈服后刚度。

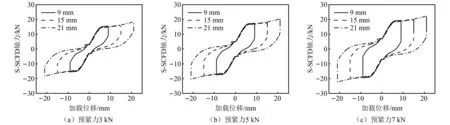
图7 S-SCFD试验滞回曲线Fig.7 Experimental hysteresis curves of S-SCFD

表4 S-SCFD力学性能参数Tab.4 Mechanical parameters of S-SCFD

由表4可知,等效黏滞阻尼比ξeq随着预紧力的增大而增大,受加载位移幅值的影响较小,增大摩擦耗能占比可有效提升阻尼器耗能性能。同时,S-SCFD的残余变形率Rdr随着加载位移幅值及预紧力的增大而增大。在预紧力为7 kN、加载位移幅值为21 mm的工况下,S-SCFD的残余变形率Rdr达到78.85 %。试验结果表明,将摩擦耗能装置与SMA并联后,阻尼器整体耗能性能随预紧力的增大而上升,而复位性能则与加载位移幅值和预紧力呈负相关。

2.3.4 双重自复位摩擦阻尼器(dual self-centering friction damper,D-SCFD)

由SMA与复位螺旋弹簧共同驱动阻尼器复位,D-SCFD具备双重复位体系。D-SCFD在各试验工况下的滞回曲线如图8所示,曲线形状同样呈“旗帜型”,各工况下的阻尼力也较为稳定。由图8可知,试件D-SCFD-2在加卸载过程中产生的阻尼力均略大于D-SCFD-1的,这是D-SCFD-2的复位弹簧刚度更大所导致的,这一现象随着加载位移的增大而越加明显。

图8 D-SCFD试验滞回曲线Fig.8 Experimental hysteresis curves of D-SCFD

D-SCFD的具体力学性能参数如表5所示。在各试验工况下, D-SCFD-1与D-SCFD-2的每周循环耗能大小W比S-SCFD的略小,最大降幅仅为17.63 J,对应的工况为: D-SCFD-2试件、21 mm加载位移幅值、7 kN预紧力。同时,双重自复位体系也增加了D-SCFD-1与D-SCFD-2的割线刚度K。与S-SCFD相比,D-SCFD-1与D-SCFD-2在各工况下的等效阻尼比ξeq有所下降,最大降幅为6.36 %,对应于21 mm加载位移幅值、7 kN预紧力的工况。

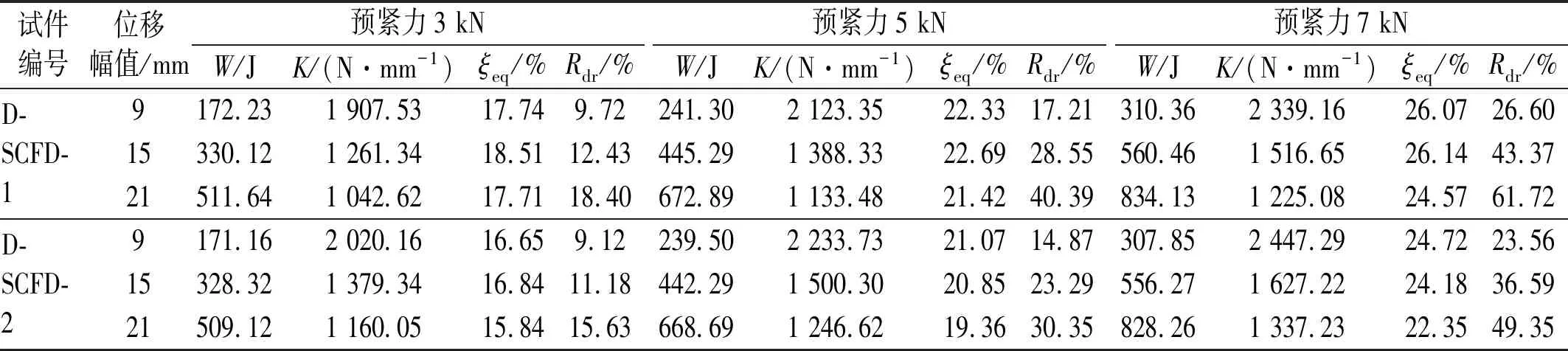
表5 D-SCFD力学性能参数表Tab.5 Mechanical parameters of D-SCFD

阻尼器等效阻尼比ξeq随着复位弹簧组件刚度的增加而大致呈线性下降,如图9所示。如前所述,双重自复位体系提高了D-SCFD-1与D-SCFD-2的割线刚度K,最大增长率分别为18.92 %和32.31 %,对应于21 mm加载位移幅值、3 kN预紧力的工况。在本试验中,复位弹簧对试件割线刚度K的影响有限,是造成等效阻尼比随着复位弹簧刚度的增加而大致呈线性下降的主要原因。

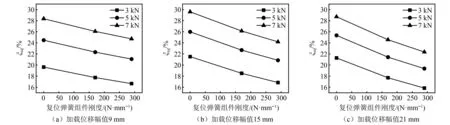
图9 不同刚度复位弹簧组件下试件的等效阻尼比变化曲线Fig.9 Equivalent damping ratio curves of the specimen under different reset springs module stiffness

由于双重自复位体系提供了更大的复位力,D-SCFD-1与D-SCFD-2在各工况下的残余变形率Rdr比S-SCFD的更小。由图10可知,当加载位移较小时,增加复位弹簧组件的刚度对阻尼器残余变形率Rdr的控制效果并不显著。增大加载位移幅值后,残余变形率Rdr随着复位弹簧组件刚度的增大而明显减小。残余变形率Rdr的下降速度随着预紧力的增大而上升,但加载位移幅值为21 mm时,下降速度随预紧力的增大而先上升后下降。在21 mm加载位移幅值、5 kN预紧力的工况下,残余变形率Rdr的降幅最大,达到35.08 %。

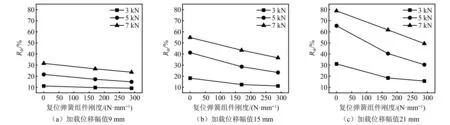
图10 不同刚度复位弹簧组件下试件的残余变形率变化曲线Fig.10 Residual deformation rate curves of the specimen under different reset springs module stiffness

试验结果反映了双重自复位体系所具备的复位弹簧有效提供了弹性复位力,并有利于提升阻尼器整体复位性能,复位性能的提升效果随加载位移幅值及预紧力的增大而愈加显著。

3 阻尼器简化力学模型和数值模拟

3.1 双重自复位摩擦阻尼器简化力学模型

新型阻尼器阻尼力由双重自复位装置及摩擦耗能装置共同提供,复位弹簧、SMA拉杆及摩擦耗能装置在外荷载作用下同时发生变形,引起双重自复位装置及摩擦耗能装置出力,简化分析模型如图11所示。

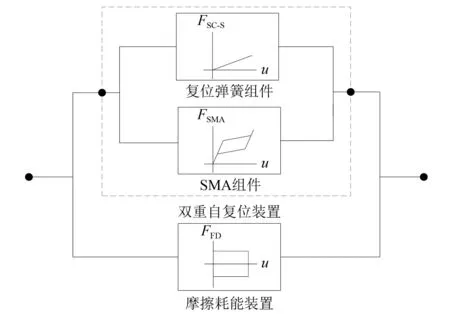
图11 双重自复位摩擦阻尼器简化分析模型Fig.11 Simplified analysis model of D-SCFD

双重自复位摩擦阻尼器恢复力公式为

FD-SCFD=FD-SC+FFD
FD-SC=FSC-S+FSMA

(4)

式中:FD-SC为双重自复位装置恢复力;FFD为摩擦耗能装置恢复力;FSC-S为复位弹簧组件恢复力;FSMA为SMA组件恢复力。

摩擦耗能装置恢复力FFD与复位弹簧组件恢复力FSC-S的计算则如式(5)及式(6)所示

(5)

FSC-S=ku

(6)

式中:P为预紧力;μ为摩擦因数; sgn(x)为符号函数;u为阻尼器位移;t为时间;k为复位弹簧刚度。

SMA组件恢复力FSMA则分段计算,如式(7)～式(10)所示

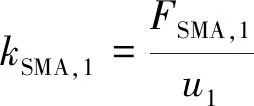
(7)

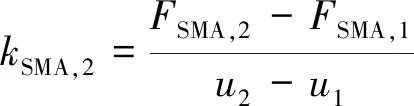
(8)

(9)

(10)

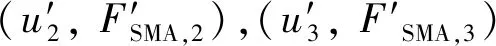
表6 SMA简化力学模型参数Tab.6 SMA Parameters of simplified mechanical model

3.2 数值模拟

3.2.1 D-SCFD有限元数值模型

为了能进一步分析双重自复位摩擦阻尼器复位性能及耗能性能,采用OpenSees两节点单元(two node link element)模拟D-SCFD,复位弹簧组件、SMA组件及摩擦耗能装置则分别通过OpenSees内置的线弹性材料(elastic uniaxial material)等刚度加卸载自复位材料(self centering material)及Bouc-Wen模型(Bouc-Wen material)模拟,最后使用并联材料(parallel material)将各组件的模拟材料并联合成D-SCFD有限元数值模型。

3.2.2 数值模型验证

对D-SCFD模型进行拉伸-压缩加载有限元模拟,并验证数值模型的准确性,模型参数及加载工况采用阻尼器力学性能试验中的D-SCFD-2试件。有限元模型的线弹性材料的线刚度按表2取290 N/mm,根据试验结果所得的自复位材料及Bouc-Wen模型材料参数分别如表7及表8所示,Bouc-Wen模型参数k0的三个取值分别对应表2中的三种预紧力。

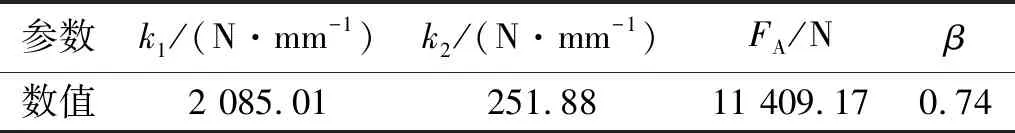
表7 自复位材料参数Tab.7 Parameters of self-centering material

表8 Bouc-Wen模型参数Tab.8 Parameters of Bouc-Wen model

简化力学模型、有限元模拟与试验滞回曲线对比如图12所示,在各工况下的简化力学模型、有限元模拟滞回曲线在加载段与试验曲线较为吻合,在卸载段存在一定的误差,这是由于SMA的实际加卸载过程并非严格的等刚度加卸载,与OpenSees自复位材料存在较小的差异,并且SMA实际滞回曲线的卸载段存在一定的曲率,与简化力学模型折线型卸载段有所不同,但简化力学模型、有限元模拟滞回曲线整体上与试验曲线拟合较好。

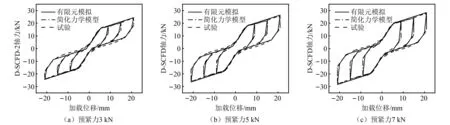
图12 简化力学模型、有限元模拟与试验滞回曲线对比Fig.12 Comparison of simplified mechanical model, finite element simulation and experimental hysteresis curves

阻尼器简化力学模型、有限元模拟与试验力学性能参数对比分别如表9、表10所示,各工况下的每周循环耗能W、割线刚度K、等效阻尼比ξeq及残余变形率Rdr简化力学模型计算结果与试验的最大相对误差分别为:6.09%、3.08%、5.09%及61.1%;有限元模拟结果与试验的最大相对误差分别为: 9.69%、3.08%、8.27%及61.46%。其中,残余变形率Rdr的误差主要源于前文所述的SMA加卸载并非为等刚度加卸载且卸载段曲线存在一定的曲率,与简化力学模型、OpenSees自复位材料存在差异,但残余变形率Rdr的绝对误差分别仅为9.55%、9.6%。综上,各项性能参数模拟结果与试验间的误差不大,简化力学模型与有限元模型能较好地模拟阻尼器的力学特性。

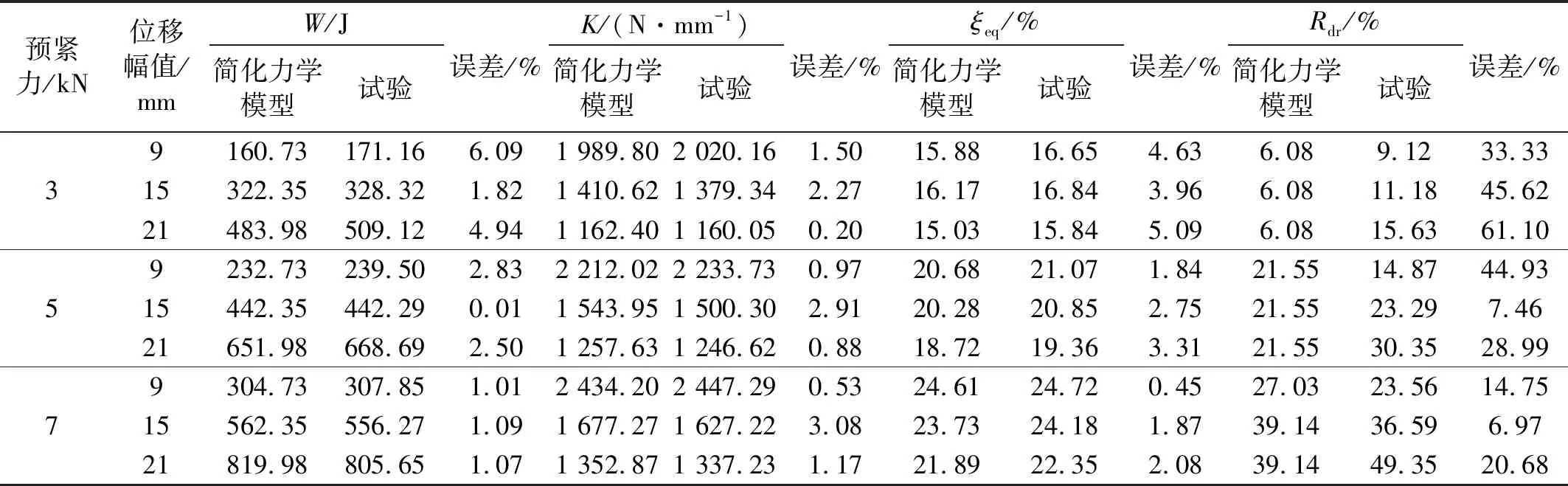
表9 简化力学模型与试验力学参数对比Tab.9 Comparison of mechanical parameters between simplified mechanical model and test

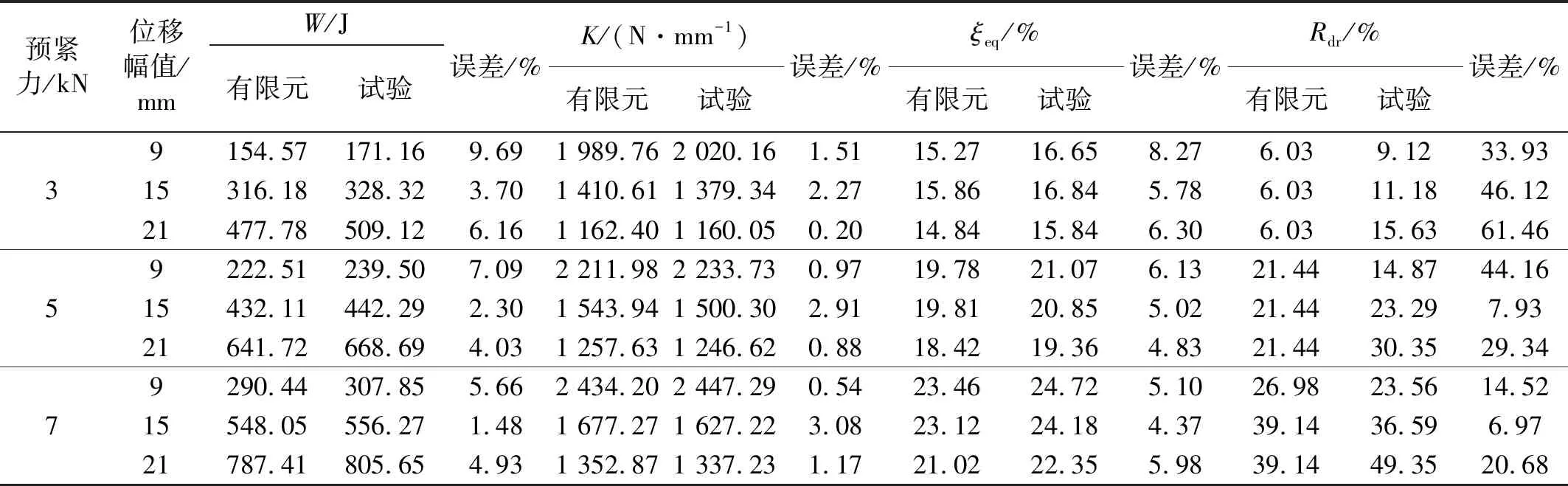
表10 有限元模型与试验力学性能参数对比Tab.10 Comparison of mechanical parameters between finite element model and test

3.2.3 D-SCFD性能分析

为进一步考察D-SCFD的耗能性能,采用上述D-SCFD有限元模型分析SMA与摩擦耗能对阻尼器整体耗能性能的贡献,并通过分析SMA与复位弹簧对阻尼器整体复位性能的贡献考察D-SCFD的复位性能。

通过图13可得,阻尼器在21 mm加载位移幅值下的每周循环加载耗能大小W随预紧力的增大而增大。相对于SMA,摩擦耗能装置对阻尼器整体耗能性能贡献较高,并随着预紧的增大而上升。当预紧力为3 kN时,摩擦耗能装置产生的每周循环加载耗能是SMA的1.06倍。当加载位移幅值为21 mm时,阻尼器整体复位率及各部件的贡献如图14所示,复位弹簧组件的刚度为SMA拉杆割线刚度的0.40倍,复位弹簧对阻尼器整体复位性能的贡献随预紧力的增大而增大。在各个预紧力下,复位弹簧对阻尼器复位率的贡献分别为2.49%、24.76%及41.85%,阻尼器整体复位率随着预紧力的增大有所下降。

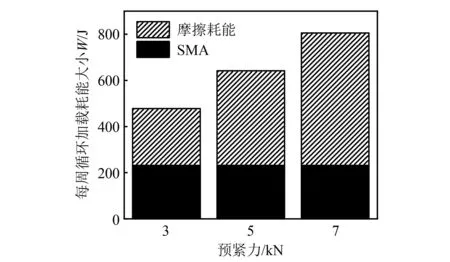
图13 D-SCFD每周循环加载耗能(21 mm)Fig.13 Energy dissipation of D-SCFD per cyclic loading (21 mm)

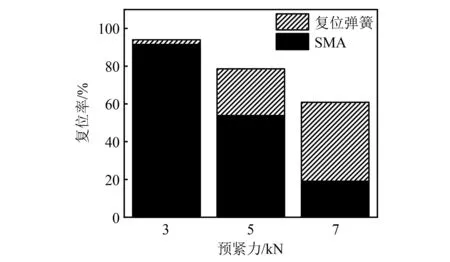
图14 D-SCFD复位率(21 mm)Fig.14 Re-centering rate of D-SCFD (21 mm)

4 结 论

提出了一种双重自复位摩擦阻尼器,并进行其模型试验及数值模拟,得出结论如下:

(1) 阻尼器残余变形率与预紧力成正相关,提供与耗能需求相匹配的复位驱动力是保证复位性能的关键。

(2) 所提出的双重自复位摩擦阻尼器具备双重复位驱动方式,易于提供更大的复位力,适配于高耗能需求,整体构造简单,受力明确。

(3) 增加复位弹簧组件刚度后,双重自复位体系可提升阻尼器复位性能,提升效果在预紧力且变形较大的情况下更加显著,但会导致等效阻尼比下降,影响耗能性能。因此,双重自复位摩擦阻尼器的设计应合理确定复位弹簧刚度、SMA直径及摩擦耗能大小。

(4) 阻尼器简化力学模型、有限元数值模拟结果与试验较为吻合,验证了数值模型的准确性。摩擦耗能装置对阻尼器整体耗能性能的贡献较大,复位弹簧对阻尼器复位性能的贡献随着预紧力的增大而愈加显著。