制动工况下重载货车车轮扁疤对轮轨振动响应分析

祁亚运, 张文谦, 张良威, 姜瑞金, 刘凤伟

(1. 重庆交通大学 机电与车辆工程学院,重庆 400074 2. 中车长江运输设备集团有限公司 科技开发分公司,武汉 430200)

随着我国国力的不断增强,重载铁路不断发展。而重载货车作为我国重载铁路的重要装备,随着轴重的提高,车轮的疲劳损伤问题在长期的运营过程也日渐突出[1]。扁疤就是最常见的车轮损伤现象,如图1所示,为重载货车车轮扁疤,车轮扁疤会对车辆的运行安全性和轮轨间的动态作用产生极大的影响。

图1 重载货车车轮扁疤Fig.1 Wheel flatofheavy haul freight vehicle

针对车轮扁疤对车辆系统的动力学影响,国内外许多学者都开展了广泛深入的研究。Maki等[2]通过试验和仿真相结合的方法,探究了车轮扁疤边缘形状对轴箱加速度的影响。Rao等[3]通过对加拿大铁路公司的车辆建立有限元模型,研究了扁疤形状、轴重、车速等一系列因素对轮轨冲击载荷的影响。Bernal等[4]通过建立Y25货车的多体动力学模型,通过车体垂向加速度来检测和识别车轮扁疤。Pieringer等[5]通过建立轮轨系统模型分析了扁疤的动态响应。王金能等[6]从轮轨材料疲劳损伤与应变率效应的角度分析了扁疤对轮轨冲击响应的影响。任尊松[7]建立了车轮踏面三维的扁疤模型,进一步探求了车轮扁疤对轮轨接触的影响。Ye等[8]通过对小尺寸扁疤的研究,发现了扁疤会引起或加剧车轮多边形。Mu等[9]通过对空载和重载条件下不同车速和扁疤长度的车辆进行仿真,得到扁疤长度与轮轨冲击力的映射关系。汪群生等[10-11]探究了轮轨损伤对动车组车体振动的影响。司道林等[12]探究了车轮扁疤对车辆临界速度以及轮轨振动的影响,并通过轨下结构载荷限值进行了扁疤的限值计算。张大伟等[13]针对30 t轴重货车和重载铁路轨道结构,研究了新、旧扁疤作用下的轮轨动力作用特征并以P1P2力为指标进行了限值计算。目前对于扁疤对于轮轨系统和车辆系统的研究已有很多,大多模型主要单一考虑了轮对或轨道弹性模态,并未结合轮轨弹性振动,同时考虑的运行状态比较简单,没有将实际的运行工况考虑在内。

在重载货车的运营过程中,制动系统是保障运营安全的最后一道防线,在制动状态下列车的动力学性能也会发生改变。刘鹏飞等[14]研究了重载货车闸瓦制动力不均衡状态下前后转向架的非对称运动。李亨利等[15]通过建立简化的大秦重载铁路列车模型,分析了列车在坡道上制动时的动力学行为,以及运行安全性的变化。Yang等[16]分析和讨论了齿轮系统在牵引和制动条件下的车轮扁疤的动态特性。Liu等[17]以1万吨和2万吨列车中的货车为研究对象,考虑了在半径400的曲线线路下,分析对比了其在紧急制动和全服役制动工况下的固化性能、对应的车钩行为和钢轨位移。目前对于重载货车制动方面的研究多是侧重于制动时的轮轨关系以及车辆的动力学特性,但并未对车轮扁疤等轮轨损伤现象考虑在内,需要进一步研究。

因此本文基于多体系统理论建立刚柔耦合动力学模型,开展制动工况下车轮扁疤对重载货车动力学性能影响的研究,同时以运行安全性为指标对不同工况下的扁疤进行限值计算,为重载货车的运营维护提供参考。

1 重载货车刚柔耦合模型

大量的研究表明,车轮扁疤会激发轮对和钢轨的高阶模态,因此有必要建立考虑轮对柔性和钢轨柔性的刚柔耦合模型,如图2所示。参照C80货车的实测悬挂参数建立刚性的车辆模型,并通过有限元分析得到轮对和钢轨的弹性模态,通过模态缩减,将柔性车轮、柔性钢轨模型和刚性车辆模型进行耦合,建立重载货车车辆-轨道刚柔耦合模型。

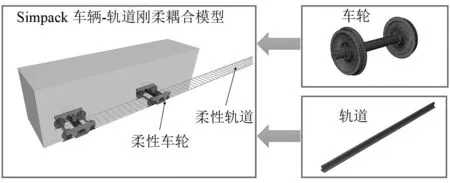
图2 重载货车车辆-轨道刚柔耦合模型Fig.2 Freightwagon-rail rigid-flexible coupling model

1.1 刚性车辆模型

为了准确模拟C80货车的运行性能,车辆模型参照C80货车的参数进行建立。C80货车采用的是三大件式转向架,整车主要由车体、侧架、摇枕、斜楔、旁承和交叉杆等组成。车体支撑在摇枕的心盘和旁承上,车体和摇枕质量经摇枕两端枕簧传递至左、右两侧的侧架,左右两个侧架通过前后两端的轴箱定位胶垫与轮对承载鞍相连接,最终传递至轨道。摇枕可相对车体转动,在心盘和旁承处产生摩擦力,形成保证车辆稳定性的摩擦回转力矩。摇枕相对侧架产生垂向、横向振动时,在楔块表面产生摩擦力,衰减车辆振动。因此车辆模型主要由车体、摇枕、侧架、轮对等组成,同时负责传递载荷的枕簧和橡胶垫视为无质量的非线性弹簧-阻尼单元。

1.2 轮轨和钢轨柔性模型

柔性模型的数学表达运用的是浮动参考系法。如图3 所示为一轮对三维模型,设其绝对参考系为X0Y0Z0,相对参考系为X1Y1Z1,相对参考系始终在质心位置,绝对参考系与相对参考系保持平行。设两个参考系之间相对位置为r,车轮上有一点P在绝对参考下坐标向量为rp,则其在相对参考下的坐标向量为u+u′,则得到公式为

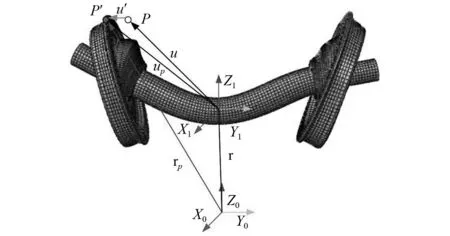
图3 柔性模型原理Fig.3 Principle of flexible model

rp=u+A01(u+u′)

(1)

式中:u为未变形状态下P点的位置向量;u′为P点变形后的位移向量;A01为相对参考系转动而产生的坐标变换矩阵,其一般形式为

(2)

用模态叠加表示P点微小的弹性位移

u′=Hpq(t)

(3)

式中:Hp为在模态集中提取出与P点相关的模态矩阵;q(t)为模态坐标。

考虑到因车轮扁疤而产生的轮轨冲击力会激发轮轨的高频模态,因此共考虑了前30阶模态频率高达1 242 Hz 的振动模态来确定轮轨响应,轮对的部分振动模态如图4(a) 所示。同时,只有考虑到钢轨的柔性模态,才能正确地模拟车轮扁疤导致的车辆轨道耦合动力学行为。与上述的轮对有限元模型相同,通过模态分析得到钢轨的模态矩阵。与仅用于力传递的柔性轮对模型不同,轨道模型需要同时考虑接触关系,将紧固件简化为弹簧阻尼单元,可以模拟钢轨的轨下接触。为了分析钢轨的动态响应,考虑了前50阶模态频率高达243.92 Hz的振动模态,钢轨的部分振动模态如图4(b)所示。

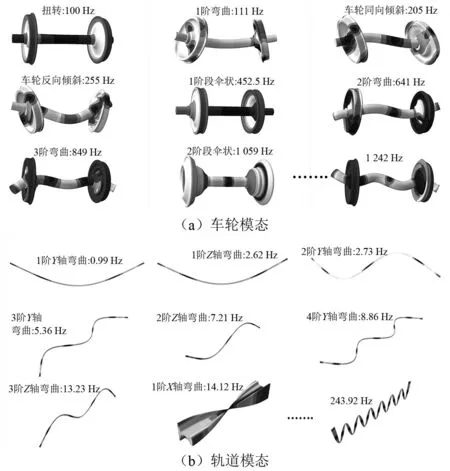
图4 车轮和钢轨部分模态Fig.4 Modes of wheel and rail

1.3 车轮扁疤

车轮扁疤建模时采用的扁疤冲击激扰模型如下式所示

(4)

式中:h=L2/(16R)为扁疤的深度;R为车轮半径;L为扁疤长度;x为沿车轮表面的弧长。通过扁疤不平顺公式我们可以得到不同长度扁疤所对应的深度分布,图5给出了扁疤长度10～60 mm范围内扁疤幅值及扁疤深度。重载货车车轮半径R=420 mm,当扁疤长度从10 mm增至60 mm时,扁疤深度由0.029 mm增至0.54 mm。

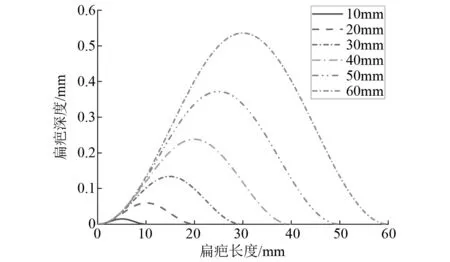
图5 扁疤长度和扁疤深度对应图Fig.5 Correspondence between flat length and depth

1.4 闸瓦制动模型

作为车辆制动系统的一部分,闸瓦制动发挥着关键的作用。本文以ZK6转向架为例,ZK6转向架采用的是单侧闸瓦制动,基础制动装置包括1个120控制阀、1个“305 mm×254 mm”旋压密封式制动缸、闸瓦间隙自动调节装置、空重车自动调整装置和高摩擦因数合成闸瓦等。

闸瓦制动时,制动缸将压力K传递给闸瓦,闸瓦与车轮相接触,因闸瓦表面摩擦因数为φk,因此闸瓦产生的制动力矩为K·φk,制动过程受力如图6 所示。

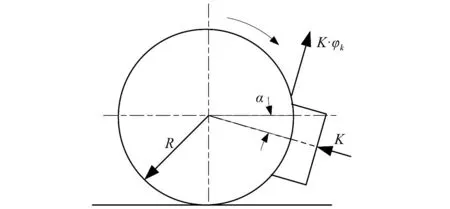
图6 闸瓦制动原理Fig.6 Braking principle of brake pads

根据TB/T 1407.1—2018《列车牵引计算规程》[18]规定,实算闸瓦压力公式为

(5)

高摩擦因数合成闸瓦的摩擦因数φk按如下式子计算

(6)

式中:v为车辆速度;pz为制动缸压力。制动缸压力一般在正常制动时为100 kPa,紧急制动时为430 kPa,在现实运行过程中,制动缸的压力并不恒定,会在理论值附近产生一定的波动。其余参数含义以及数值如表1所示。

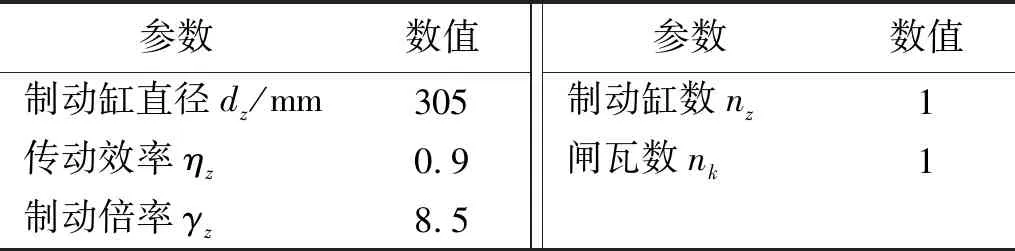
表1 闸瓦制动力计算主要参数Tab.1 Main parameters of brake force calculation

1.5 车辆模型试验验证

首先对比刚性模型与刚柔耦合模型在相同速度与相同扁疤工况下进行仿真计算,轮轨力的对比结果如图7所示。可以看出在刚性模型下,车轮在经过扁疤的作用下形成的冲击并不具有P1P2力的特征,且车轮出现了跳轨现象,将轮轨模型柔性化处理能更好地反映出轮轨高频振动响应,采用刚柔耦合模型后能够更加准确地得到扁疤引起的振动响应。

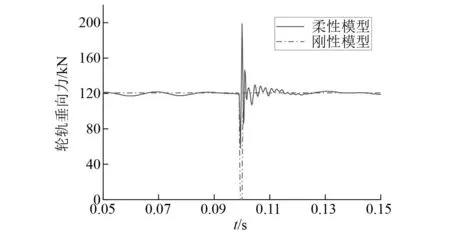
图7 轮轨垂向力Fig.7 Wheel-rail vertical force

将仿真结果与重载货车实际测量数据进行比较,通过比较侧架的垂向加速度来验证模型的准确性。如图8所示为实测与仿真模型侧架垂向加速度的时域图与频谱图。由图8可知,试验与仿真的垂向加速度都是主要分布在-5 m/s2与5 m/s2之间。从频谱图上可以看出,在0～25 Hz之内垂向加速度的振幅大部分都是在0.1 m/s2内分布,振动主频都为3 Hz,10 Hz左右。考虑到实际线路上其他因素的影响,实测数据会产生较大波动。通过对比侧架垂向加速度,仿真模型在时域和频域接近。因此通过上述方法建立的轨道-车辆刚柔耦合模型能够有效地模拟车辆运行状态。

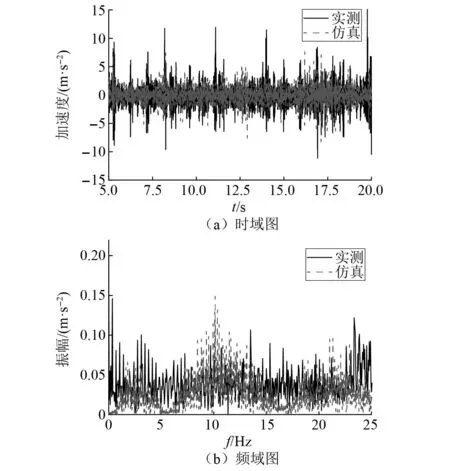
图8 侧架垂向振动加速度Fig.8 Vertical vibration acceleration of the side frame

2 制动工况下扁疤作用时轮轨振动响应

2.1 不同制动工况下的轮轨力动态响应

为了探究重载货车在不同制动工况的动力学特性,在正常制动工况与紧急制动工况下行驶,得到不同扁疤下车辆不同时间段的轮轨动态响应。

闸瓦制动的原理是通过制动缸将压力施加在闸瓦上,正常制动和紧急制动工况下的制动力如图9所示。正常制动闸瓦力是通过实测制动缸的压力进行计算得到,闸瓦压力从15 s时开始加载在25 s达到最大值最后一直维持在8 kN左右。紧急制动闸瓦力是通过牵引计算规程规定的列车管压力计算而得,其加载时间同样是10 s最后闸瓦压力维持在30 kN左右。

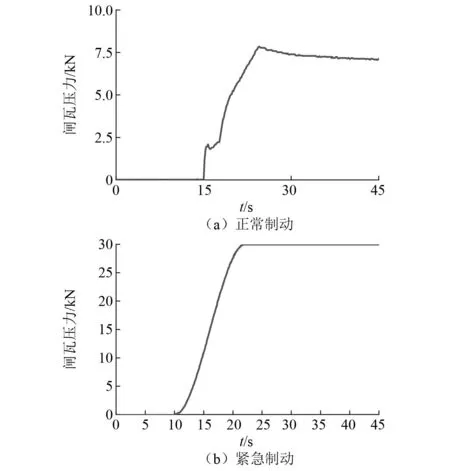
图9 闸瓦压力Fig.9 Brake pressure

车辆在行驶的过程中,由于扁疤会对车辆产生垂向冲击,这一现象会体现在垂向轮轨力会因扁疤产生波动。图10为紧急制动和正常制动下不同扁疤所引起的垂向轮轨力时域图,可以看出轮轨力波动随着扁疤长度增加而增大,且这些轮轨力都包含了轮轨冲击P1力和P2力。对比发现紧急制动工况下轮轨力均值会大于正常制动。当扁疤长度为60 mm时,正常制动工况下为216 kN,紧急制动工况轮轨力最大值为228 kN,增大了5.6%。

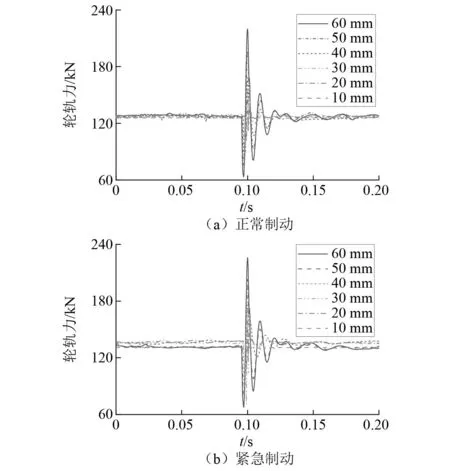
图10 轮轨力时域图Fig.10 Time domain of wheel-rail vertical forces

因扁疤而产生的轮轨垂向力主要有两个典型的特征力即P1和P2力。P1力为车轮和钢轨通过Hertz弹性接触而产生的高频冲击力,P2力为整个车辆系统和轨道结构受扁疤冲击而出现的低频响应力。车辆在不同的工况下,其P1力和P2力会有明显的不同。图11为车辆在不同扁疤长度下,制动过程中的P1力和P2力的变化,由于整个制动过程较长,选取了两个速度节点,分别为54 km/h和36 km/h。可以看出P1力和P2力随速度和扁疤长度增加而增大。速度和扁疤对P2力没有明显的影响,但对P1力的影响较大,当扁疤长度60 mm时,正常制动工况下P1随速度减少了10 kN,紧急制动工况下P1随速度减少了13 kN。相较于速度变化,扁疤长度的变化对P1力的影响更大。随着扁疤长度从10 mm增长到了60 mm,P1力的增长倍率普遍达到了180%。同时紧急制动下的P1力和P2力普遍大于正常制动,但在数值上并没有太大差距。

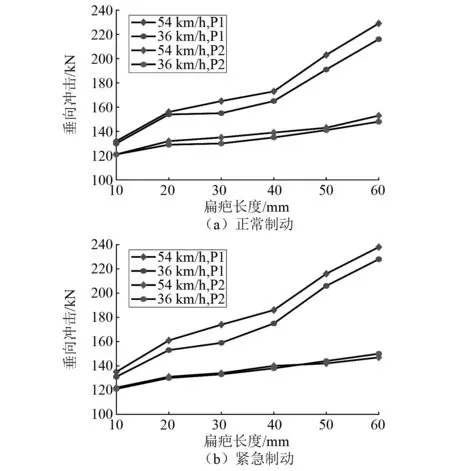
图11 不同制动工况Fig.11 Different braking conditions

2.2 制动工况下车辆载荷对轮轨动态响应的影响

重载货车在服役的过程中也会面临车辆载荷变化的情况,货车在空载时静轴重以及轮轨力都会发生改变,在空载状态下扁疤对车辆的影响与重载状态完全不同,因此有必要研究空载下货车振动。如图12所示,在相同速度且没有扁疤作用下,重车和空车因自身载荷的不同,其轮轨力会不相同。重车的垂向轮轨力为127 kN,空车的垂向轮轨力为24 kN。在60 mm扁疤的作用下,空车的垂向轮轨力波动大于重车,且空车出现了瞬时的轮轨力为零的现象,这说明轮轨之间会出现短时间的轮轨分离。从两个时频图中可以看出,两种工况下的主频分布都集中在400～500 Hz和600～1 000 Hz这两个区间,这也正好对应了车轮的1阶伞状和2阶、3阶弯曲模态频率。不同的是,空车工况下其能量普遍小于重车工况。尤其是重车工况下,低阶频率能量远大于空车,这说明在重车工况下扁疤损伤更容易引起轨下结构的破坏,主要是由于重车激发的轮轨模态响应更大。

图12 60 mm扁疤作用下空车与重车垂向轮轨力Fig.12 Wheel rail vertical force of the empty and heavy vehicle under the 60 mm flat

空载紧急制动状态下轮轨力统计如图13所示,空载车辆在紧急制动时,其P1和P2力的变化和重载车辆一样,都是随着扁疤和速度增加而增大。但不同的是,空载下P1和P2力的增加幅度都远远大于重载,其P1和P2值随扁疤长度增长背书都达到了250%。而重车状态下P1和P2值的增长倍数分别为176%和120%。

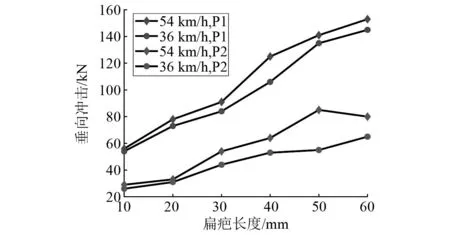
图13 空载紧急制动Fig.13 Emergency brake conditionofthe empty vehicle

3 制动工况下的纵向蠕滑和摇头角

当车辆在进行闸瓦制动时,闸瓦与车轮踏面相接触会增大转向架对轮对纵向和摇头的约束,因此车辆纵向蠕滑状态会因为制动状态而发生改变。另一方面车轮扁疤会引起轮轨接触关系的变化,产生高频震荡,从而破坏蠕滑状态。

(7)

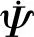
闸瓦制动会导致车轮运行状态发生改变,摇头角速度就包括在内,同时扁疤所造成的冲击也会使摇头角速度产生波动如图14(a)所示。

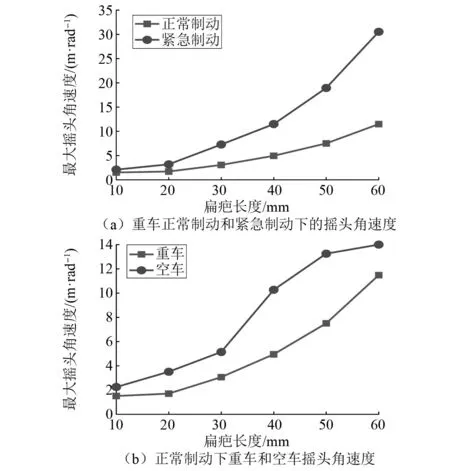
图14 摇头角速度最大值Fig.14 Yaw angle velocity maximum value

在不考虑扁疤的状态下车辆分别进行制动与紧急制动时都会发生纵向蠕滑率与蠕滑力的变化。紧急制动所导致的纵向蠕滑率和蠕滑力分别为0.071%和10 kN要远大于正常制动的0.036%和5.8 kN。当考虑车轮扁疤时,正常制动和紧急制动工况下的纵向蠕滑率和最大纵向蠕滑力都随着扁疤长度的增加而增加,当扁疤长度达到60 mm时,紧急制动工况下的纵向蠕滑率和最大纵向蠕滑力分别为0.137%和26 kN而正常制动为0.096%和10.5 kN。相较于不考虑扁疤的状态下,正常制动工况下纵向蠕滑率和最大蠕滑力增长了166.7%和81%,而紧急制动工况下增长了92.95%和160%。

而如图15所示,空车正常制动与重车正常制动工况下,车辆的纵向蠕滑率几乎相同。而不考虑扁疤的状态下,空车纵向蠕滑力要远远小于重车。而空车最大的纵向蠕滑力却产生了非常大的增长,其增长幅度高达7.5倍,这是由于扁疤对空车产生了轮轨冲击过大,从而使得60 mm扁疤作用下空车的最大纵向蠕滑力大于重车的最大纵向蠕滑力。

4 重载货车车轮扁疤限值计算

车轮扁疤所引起的巨大轮轨力将对轨道结构产生显著的破坏的效果,造成轨道结构服役周期缩短以及维修养护成本的增加,因此有必要在日常检修中对车轮扁疤进行有效控制和及时镟修,计算扁疤限值可以为重载车辆日常维修提供参考。

文献[12]和文献[13]都对重载货车的扁疤限值进行了计算,其计算出的结果与方法如表2所示。目前对于扁疤限值计算的研究大多是针对地铁和高速动车,对于重载货车国内并没有相关指标,只能通过国外建立的规范和从安全性的角度出发来进行计算。

UIC518中规定,最大运营时速不超过100 km/h的车辆轮轨力不应超过200 kN[21],因此垂向轮轨力的限值不应超过此值。利用上述模型计算的轮轨垂向力最大值如图16(a)所示,在轮轨力达到200 kN时,正常制动工况下扁疤长度限值为49 mm,紧急制动工况下扁疤长度限值为44.5 mm。

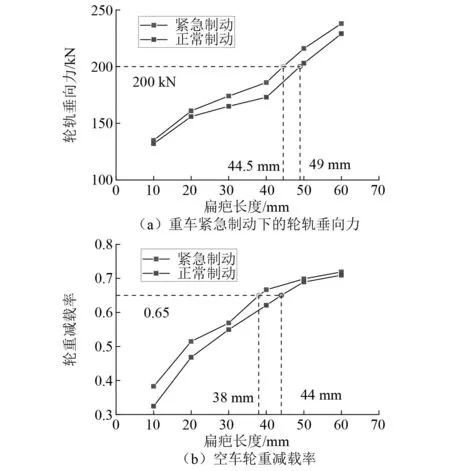
图16 扁疤限值Fig.16 Limit values for wheel flat

虽然空车状态下车辆轮轨垂向力小于重车状态,但其在扁疤状态下的垂向力波动要远远大于重车,这会导致车辆有脱轨的安全风险,因此我们采用轮重减载率来计算空车状态下的扁疤限值。根据GB 5599—2019《铁道车辆动力学性能评定和试验鉴定规范》[22]规定,铁路车辆的轮重减载率限值为0.65。计算空车轮重减载率如图16(b)所示,当空车轮重减载率为0.65时,正常制动工况下扁疤限值为44 mm,紧急制动工况下扁疤限值为38 mm。与参考文献结果相比较可以发现,在考虑各种综合因素的情况下,将扁疤长度控制在38 mm是一个合理的选择。

5 结 论

为了探究制动工况下重载货车车轮扁疤的振动响应,本文建立了重载货车轨道-车辆刚柔耦合动力学模型。分析了不同制动工况和不同扁疤长度下的轮轨冲击载荷,并对车轮扁疤限值进行了计算。得出以下结论:

(1) 随着扁疤长度和速度的增加,车辆的P1和P2力会增大,P1力的增加幅度在176%左右,且紧急制动工况下P1和P2力略微大于正常制动工况。空车状态下轮轨力小于重车状态,但其垂向轮轨力的波动要远大于重车,且其P增幅达到了280%。

(2) 在制动工况下轮轨之间的纵向蠕滑力和蠕滑率会因扁疤所造成的冲击而产生波动,扁疤长度越大波动幅度越大。在紧急制动工况下纵向蠕滑力和蠕化率大于正常制动。而空车状态时,其纵向蠕化率与重车数值接近,但蠕滑力变化幅度差异较大。

(3) 通过轮轨垂向力和轮重减载率两项安全性指标,计算出在紧急制动工况下重车扁疤限值为44.5 mm,空车限值为38 mm,在正常制动工况下重车扁疤限值为49 mm,空车限值为44 mm。因为紧急制动工况属于特殊工况,且极短时间内轮轨力的波动对轮轨系统影响较小,建议在实际运营过程中控制扁疤长度在 38 mm以内。