高精度激光共焦半导体晶圆厚度测量

李兆宇，刘子豪，王瑶莹，邱丽荣，杨 帅

（北京理工大学 光电学院 复杂环境智能感测技术工信部重点实验室，北京 100081）

1 引言

晶圆作为集成电路（IC）芯片、发光二极管（LED）、太阳能电池和MEMS 器件等半导体产品的衬底，是高度纯净的晶体结构，对其减薄有利于堆叠以获得更高的性能［1］。随着技术的发展，研磨后的晶圆厚度更薄，尺寸更小，精准且可靠的晶圆厚度表征是晶圆厚度控制的先决条件，有助于提升器件一致性和质量稳定性，而在切割、蚀刻与抛光过程中反复装卸测厚会增加表面损坏的风险，因此，当晶圆吸附在支撑板上时进行高精度无接触测量至关重要。

Park 等［2］提出了一种谱域干涉测量方法，可测大型硅片的物理厚度、折射率、弯曲和翘曲，但测量结果的不确定度为0.692 μm，测量精度有待提升。Kim 等［3］使用波长调谐干涉法同时测量了晶圆的表面轮廓和光学厚度偏差，但干涉法引入的耦合误差会带来系统误差。Yan 等［1］基于迈克尔逊干涉原理，使用1 550 nm 红外光对掺杂硅片实现快速检测，但其测量结果受步进电机定位精度和空气干扰较大，由于定位误差的存在，晶圆的厚度重复性在2 μm 左右。Zeng 等［4］使用补偿式电感测量方法，对标准硅片的测量不确定度达0.2 μm，但其装置过于复杂，且是接触式测量，极易损伤晶圆表面。Hirai 等［5］开发出一种双面干涉仪，可实现非接触测量，但测量过程中需要将两个测头相对放置在样品两侧，频繁拆卸极易造成晶圆损坏。

综上所述，半导体晶圆厚度测量目前仍然面临重复测量精度较低、保证精度的同时无法实现表面无接触无损测量等问题。激光扫描共聚焦显微镜（Laser Scaning Confocal Microscopy，LSCM）具有高分辨率、独特的光学层切能力、无损测量等特性［11］，广泛应用于微电子［6-7］、半导体检测［8-9］、材料科学［7，10］等领域。因此，基于高精度激光共聚焦技术的晶圆厚度测量提供有效的解决途径。

本文利用LSCM 峰值点与定焦位置对应的特性实现层析定焦，结合大行程高精度音圈纳米位移台完成轴向驱动扫描，对晶圆的不同表面进行高精度定焦并计算得到其光学高度坐标，建立光线追迹模型实现物理坐标计算，得到不同种类晶圆的物理厚度，实现了晶圆厚度的高精度、在线、无损检测，可为工艺优化提供参数依据，对于提升半导体器件的生产效率和产品质量具有重要意义。

2 测量原理

2.1 激光共焦晶圆定焦测量原理

激光共焦探测原理如图1 所示，点光源和点探测器处于彼此共轭位置，共焦系统光强值会随着被测件的轴向离焦移动而变化，形成“钟形”曲线。该特性成为共焦技术区别传统显微技术的显著特性，可以实现被测表面的定焦测量。当测量光束汇聚在晶圆表面时由探测器接收到的信号为I（u），根据共聚焦成像原理［12-13］，经归一化处理得到的共焦光强轴向响应为：

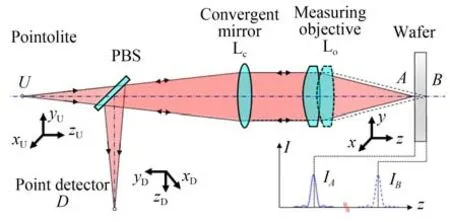
图1 共焦系统层析定焦原理Fig.1 Confocal system chromatographic focusing principle

式中：ρ是光瞳面的归一化极径，u为轴向位置z的归一化光学坐标：

其中：λ为单色激光光源的波长，DL为激光有效通光口径，f0为会聚镜的焦距，z为被测表面的轴向位置。联立式（1）和式（2）可得共焦光强响应信号为：

如图1 所示，会聚镜将点光源的发散光束会聚为平行的测量光束，光路中引入光束调制器件以提高光路性能，测量物镜将平行的测量光束会聚到待测点并收集返回光。这种光路设计便于更换物镜从而适应不同参数的被测物，进而更改测量光束口径和工作距离。在对晶圆上表面A点进行定焦测量时，共焦曲线的最大值IA（z）正好对应于被测面点A的位置，直到测量光束汇聚到另一个被测表面B点。为了获得共焦曲线，使用峰值检测算法寻找共焦曲线的峰值点，使用最小二乘法生成所有归一化坐标值大于0.8 的拟合曲线，最后计算出峰值坐标，得到被测点A和B的光学位置。当测量物镜沿轴向对晶圆进行扫描探测时，晶圆的每个反射层面均会有反射光返回光路。此时，探测器探测到的总光强为系统对各个层面响应的相干叠加，探测到的总光强为：

其中：Ki为第i个面的振幅反射率，ui为第i个面的物方归一化轴向坐标。当样品不同表面之间的间距较小时，如图2（a）所示，两个表面的反射信号会混叠，对应的峰值点淹没在叠加信号中无法识别；当两个表面间的间距增大时，如图2（b）所示，两反射面对应的钟形曲线初步分离，总信号曲线出现两个峰值；当间距进一步增大时，如图2（c）所示，两表面对应的钟形曲线完全分离，相互没有影响，总的响应曲线中两表面信号峰值明显，可以对不同表面进行层析定位。根据瑞利判据，两信号叠加，曲线最小值为最大值的73.5%时，两峰值之间的中心距为系统能够分辨的最小间距，曲线如图2（b）所示。当样品不同表面之间的物方归一化间距大于当前Δu=6.58 时系统即可分辨，进而进行层析定焦探测。

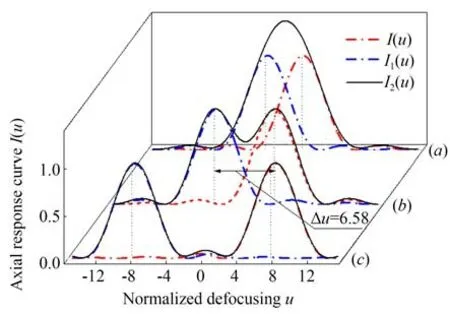
图2 两个反射层的综合响应Fig.2 Combined response of two reflective layers

2.2 晶圆物理厚度计算原理

晶圆上表面A点的共焦轴向响应曲线峰值点坐标记为ZA-i（i=1，2，…，nT），当定焦至下表面B点时，由于存在折射率n，测量光线穿过晶圆上表面后发生偏转，所得B点轴向响应曲线峰值点ZB-i（i=1，2，…，nT）为其光学位置坐标，并非所需要的物理坐标（i=1，2，…，nT）。为得到晶圆表面高度的物理位置坐标，在建立归一化共焦点扩散函数测量模型后，给出了光线追迹模型［14］，如图3 所示。

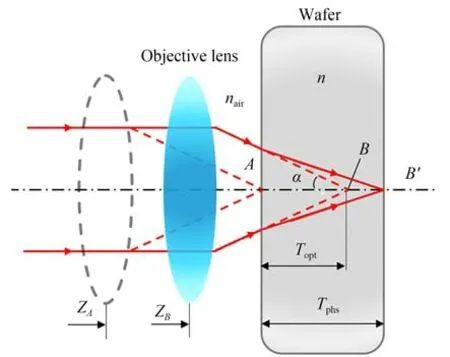
图3 晶圆内部光线追迹模型Fig.3 Internal light tracing model of wafer

根据几何关系，晶圆上表面与下表面的层间光学厚度Topt为：

根据光线追迹公式分析，晶圆上表面与下表面的层间物理厚度为：

式中：n为晶圆内部介质折射率，α为测量光束的半孔径角，R为待测样品的曲率半径。由于被测晶圆表面为平面，取R=∞，式（6）可化为：

函数Tphs(n，R，Topt，α)只对应半孔径角α内一条光线的测量结果，轴向空间应由整个瞳孔平面内的所有测量光线积分计算。假设光线在瞳孔平面内均匀分布，则晶圆厚度Tphs满足：

则晶圆下表面顶点的物理位置坐标ZB为：

3 测量传感器构建

3.1 系统设计

激光共焦晶圆厚度测量传感器系统框图如图4 所示。为满足不同透过率晶圆样品的测量需求，使用相同的测量光路结构，配合波长为633 nm 和1 064 nm 的20 mW 单波长激光器，分别完成了不同波段的传感器搭建。由激光器发出的平行光经过扩束系统中的针孔形成近似理想的高斯球面波，球面波经扩束系统后形成可充满物镜后瞳的平行光，由PBS 选择P 偏振光进入测量光路，经过与P 光呈45°放置的1/4 波片后变为左旋圆偏振光，由物镜聚焦到被测样品表面。然后，返回的带有样品表面位置信息的右旋圆偏振光经过1/4 波片后变为S 光，经PBS 反射后全部进入会聚镜PL，避免光返回到激光器中影响激光器稳定性。会聚光束经过NewPort 物理针孔PH 后杂散光被滤除，进而进入放置在焦点位置处的光电探测电路中，完成光信号探测与电信号的转换。

图4 激光共焦半导晶圆厚度测量传感器系统框图Fig.4 Block diagram of laser confocal semiconducting wafer thickness measurement sensor system

如图4所示，通过音圈纳米位移台驱动物镜沿光轴方向对晶圆表面采样点位置扫描定焦，依据电机实时反馈的位置信息与探测电路得到的光强电压信息得到用于层析定焦测量的归一化激光共焦轴向响应曲线，曲线峰值点坐标即为定焦处的光学位置。控制器通过读取上位机控制指令完成电机使能、参数设定、运动驱控等操作，同时，获取传感器光栅模拟量读数头细分后的位置检测信号并进行负反馈控制。经514 倍细分后的光栅尺信号可识别电机1 nm 的微小位移。高精度音圈纳米位移台为本课题组自研成果，行程最大可达5.7 mm，分辨力优于1 nm，100 μm 频响优于30 Hz，既可以保证高动态定焦触发瞄准，又能兼顾轴向大范围微位移测量。系统构建实物如图5所示。

图5 激光共焦半导晶圆厚度测量传感器系统实物Fig.5 Physical map of laser confocal semiconducting wafer thickness measurement sensor system

3.2 核心器件参数仿真

根据激光共焦测量光路可知，该传感器的主要影响参数包括测量物镜的数值孔径NA、会聚镜PL 的焦距f0以及针孔物理半径rd。

3.2.1 测量物镜的数值孔径

受晶圆制备工艺的影响，由式（8）可知，物理坐标计算过程中，晶圆内部折射率分布误差Δn与物镜数值孔径NA 均会影响物理厚度测量，而数值孔径NA 又是决定轴向定焦分辨力Δu及横向分辨力Δv的关键因素，即：

这里以硅片样品为例，取空气折射率nair=1，λ=1 064 nm，信噪比（Signal-to-Noise Ratio，SNR）取300，根据光线追迹公式仿真得到当Δn=10-4及nˉ=3.42 时，对应不同的测量物镜数值孔径NA，晶圆内部折射率不均匀性Δn对晶圆物理厚度Tphs测量结果的影响，如图6 所示。根据式（10）仿真得到物镜数值孔径NA 对传感器轴向定焦分辨力Δu及横向分辨力Δv的影响曲线，如图7 所示。

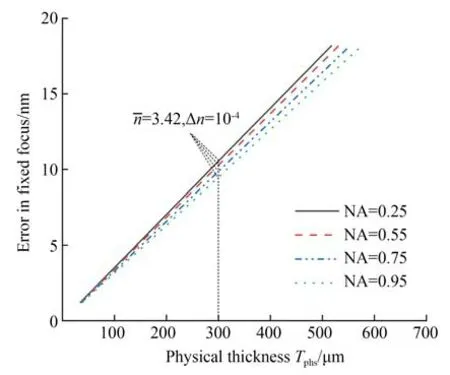
图6 NA 不同时Δn 对Tphs的影响Fig.6 Influence of Δn on Tphs with different NA

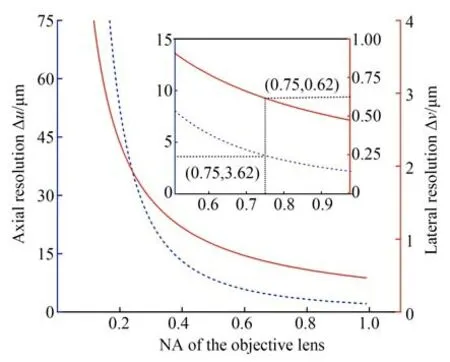
图7 NA 对Δu 及Δv 的影响Fig.7 Influence of NA discrepancy on Δn and Δn

由仿真结果可知，当晶圆内部介质存在折射率不均匀性Δn时，定焦误差随着样品厚度的增加而变大，物镜数值孔径NA 越大，厚度Tph一定时由Δn引起的定焦误差越小，系统的轴向定焦分辨力Δu及横向分辨力Δv越高，但通常情况下物镜NA 值和工作距是呈负相关的，NA 值越大工作距便越小，极易在晶圆在线测量过程中与加工设备产生碰撞。因此，针对不同样品仿真结果综合考虑，对应1 064 nm 波段硅片等样品选用NA=0.75 近红外显微物镜，其工作距离为DW=12 mm。据2.1 节分析，此时共焦系统可分辨的物方间距为：

对应633 nm 波段SiC 等样品选用数值孔径NA=0.55 的显微物镜，工作距离DW=8.7 mm，可对Δz=2.19 μm 的物方间距进行层析定焦。

3.2.2 会聚镜焦距

除物镜NA 直接影响分辨力Δu外，Δu还与共焦曲线斜率有关，而后者直接受针孔轴向离焦量uM的影响。uM和实际离焦量MOP与会聚镜焦距f0的关系如下：

当物镜NA=0.75，光源波长λ=1 064 nm，根据式（12）仿真得到会聚镜PL 焦距f0不同时，针孔的实际离焦量MOP与轴向灵敏度Δu的关系，如图8 所示。由图可知，离焦量MOP与轴向定焦分辨力Δu呈负相关，MOP越大分辨力越高，变化趋势为先快后慢；会聚镜PL 焦距f0越大，轴向分辨力Δu随离焦量MOP的变化幅度越不灵敏，针孔装调精度要求降低。然而，较大的焦距f0会延长整体测量光路，增大传感器体积，难以满足小型化的同时还会引入不必要的误差源。因此，综合考虑对应1 064 nm 波段硅片等样品，选择焦距f0=200 mm 的会聚 镜，结 合633 nm 波 段SiC 等样品的仿真结果，同样选择f0=200 mm 的会聚镜焦距。为了减小传感器体积，综合光斑尺寸，测量光路中棱镜及透镜尺寸均小于等于10 mm。

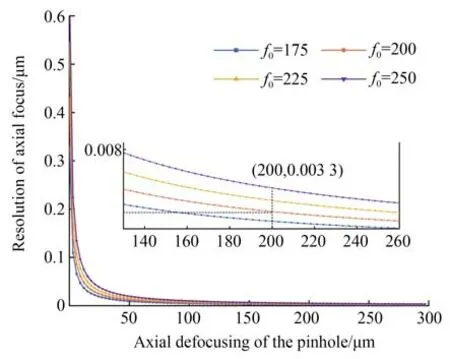
图8 f0不同时MOP与Δu 的关系Fig.8 Relationship between MOP and Δu with different f0

3.2.3 针孔的物理半径

针孔作为共焦系统的关键部件，其物理参数会对系统的信号强度、信噪比以及轴向分辨力产生影响。设rd为圆形针孔的半径，由式（2）其归一化半径为vd，由于在实际光路中不存在理想点探测，有限尺寸的探测器可以得到激光共焦光强响应：

通常情况下，系统轴向响应曲线的半高宽可用于评估系统的空间分辨能力。vd取不同值时的轴向响应曲线如图9 所示。共焦系统的轴向响应曲线中半高宽和峰值强度均随着针孔归一化半径vd的增加而增加，且变化趋势也不相同。在此基础上，仿真得到归一化半径尺寸vd不同时曲线参数变化，如图10 所示。

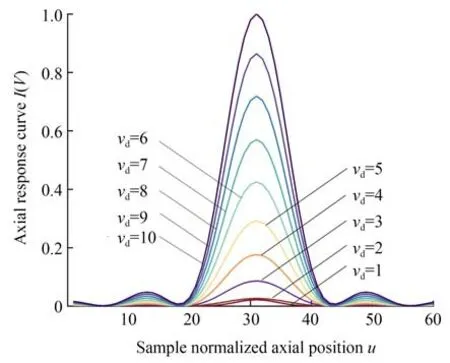
图9 不同针孔尺寸下的轴向响应曲线Fig.9 Axial response curves for different pinhole sizes

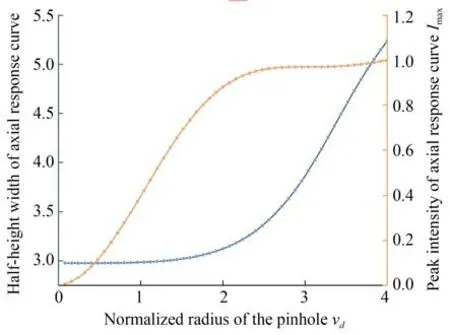
图10 归一化半径不同时曲线参数变化Fig.10 Variation of curve parameters with different normalized radii

由图10 可知，vd＜2 时，轴向响应曲线的半高宽较低，峰值强度迅速增加；当vd≥2 时，峰值强度趋向稳定，而半高宽开始增加。为了使传感器性能达到最佳状态，需要取较大的峰值强度和较小的半高宽，故针孔归一化半径vd=2，带入式（14）可得出针孔的实际物理半径：

rd(1064)≈50 μm，rd(633)≈35 μm，结合具体产品型号，对应1 064 nm 和633 nm 波段分别选用NewPort 直径为100 μm 和75 μm 的针孔。

4 误差分析

针对激光共焦半导体晶圆厚度测量系统，分析可能的误差来源并进行误差计算，以保证激光共焦晶圆厚度检测技术的可靠性。

4.1 共焦光路定焦误差

激光共焦方法本身存在定焦误差，受光路多个参数的影响。针对硅片等样品激光器光源波长选用1 064 nm，测量物镜的数值孔径NA=0.75，针对碳化硅等样品选用波长633 nm，NA=0.55，轴向归一化离焦量uM=2.5 时，响应曲线的最大斜率Smax=0.27，系统信噪比SNR=300∶1，此时1 064 nm 波段共焦定焦误差为：

同理计算出633 nm 波段的定焦误差约为4.13 nm。

4.2 音圈纳米位移台定位误差

传感器由音圈纳米位移台进行轴向运动控制，后者直接影响测量精度，通过测量不确定度为±0.5×10-6（k=2）的Renishaw XL-80 激光干涉仪进行标定。标定后定位误差为：

4.3 随机误差

晶圆厚度测量过程中环境噪声、气流扰动、光源波动和操作人员等因素均会引入测量误差，主要表现为随机误差。将上述随机因素考虑在内，使用相同工作状态下的检测重复性来表示：

待系统调整完成状态稳定后，取N=10，进行重复实验测试，测得系统δ3=23 nm。

4.4 晶圆内部折射率误差

光线追迹公式（7）是以晶圆内部材料折射率均匀分布为前提的，受制备工艺和测量方式的限制，晶圆内部会存在折射率分布误差Δn。以硅样品为例，根据式（8）分析得出，当分布误差Δn=10-4=3.42 时，该误差对物理厚度计算的影响：

4.5 误差合成

上述各个误差源相互独立，计算得所研制的传感器系统的测量误差为：

同理计算出其余5 种晶圆的合成误差分别为：δGaAs≈38 nm，δCaN≈34 nm，δAl2O3≈49 nm，δSiC≈δHR-SiC≈29 nm。

5 特性测试及实验验证

5.1 光学分辨力测试

以共焦光强响应曲线可区分的最小步距来评价传感器的轴向定焦分辨力。将平面镜放置在测量物镜焦点附近，此时光强响应信号最强，由音圈纳米位移台驱动物镜进行轴向小步距运动，同时，记录光栅尺位置信号和24 位NI 系列数据采集卡获取的光强响应信号，实验结果如图11 所示。音圈位移台每进行5 nm 的轴向位移运动，传感器的响应光强也按规律呈现步进状态，因此，传感器可分辨出5 nm 的位移变化。

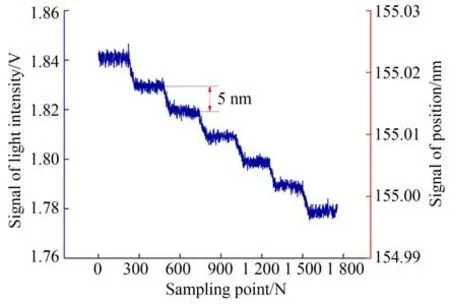
图11 光学分辨力测试Fig.11 Optical resolution testing

5.2 轴向量程测试

为验证传感器的轴向行程范围，利用光栅尺监测音圈位移台的位移，光栅尺得到的最大位置信息与最小位置信息的差值即为传感器的最大移动范围。由于在光栅尺装调时已将其零刻线位置对准音圈位移台最上端，并将此位置设为初始零位，因此，测量时将位移台“回零”后开始驱动显微物镜使之移动最大距离。光栅尺重复测量5 次，测试结果如表1 所示。

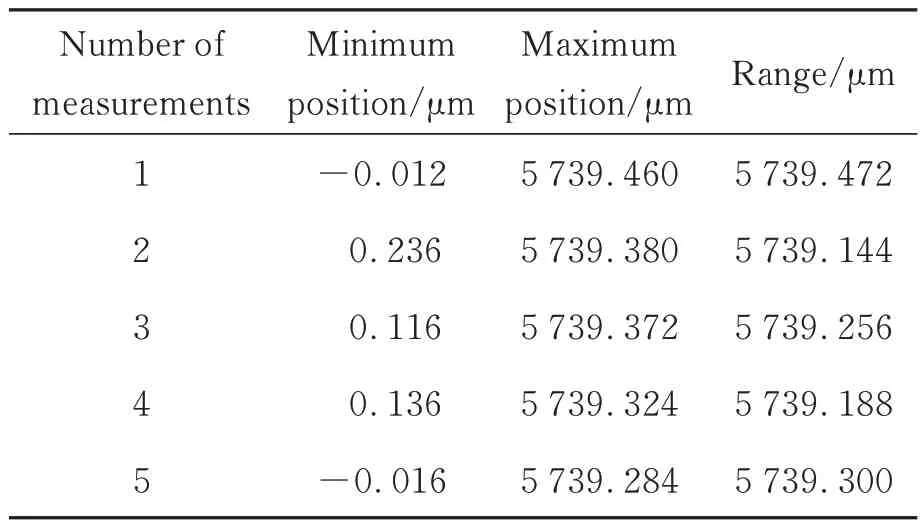
表1 轴向量程测试结果Tab.1 Results of system axial measurement range testing

从测试结果可知，利用光栅尺配合音圈位移台，整个系统可以实现5.7 mm 行程内样品的定焦测量。

5.3 重复性测试

为了评估传感器的稳定性，待系统调整完成并处于稳定工作状态下，控制音圈位移台驱动物镜使其焦点多次经过反射镜表面，完成沿光轴方向的多次扫描。由于激光共焦测量方案为峰值点触发，所以重点测试响应曲线峰值点的重复性。对同等条件下多条共焦曲线的测量结果进行数据处理，得到如表2 所示的峰值点坐标，10次测量的重复性标准差为23 nm。从结果可以看出，该传感器具有良好的重复性。

表2 激光共焦传感器峰值点重复性测试结果Tab.2 Repeatability test results of laser confocal sensor peak point

6 对晶圆样品的测试与分析

测试样品如图12 所示，分别选用用于集成电路制造的一代半导体（Si）、服务光通信产业的二代半导体（GaAs），以及拥有更广阔前景的三代半导体（GaN，Al2O3，SiC，HR-SiC（High Resistance SiC））进行测量。为避免托盘表面的反射光进入光路影响测量信号，将晶圆定焦测量位置处悬空处理。通过程序计时得到单次厚度测量时间小于400 ms，实现了快速检测。

图12 半导体晶圆样品Fig.12 Samples of different semiconductor wafers

测量开始前，首先进行轴向寻焦定位，调整传感器位置使待测晶圆移动至测量物镜的工作距内，由上位机软件控制音圈位移台驱动物镜在量程内做大范围轴向运动，待探测电路检测到外表面光强时，获取当前光学位置信息，程序控制物镜移动至当前采样点上约100 μm 处，设置采样率、运动速度、加速度减速度后，开始单次检测。图13 为激光共焦传感器对上述6 种晶圆样品进行扫描测量得到的单次信号曲线。光线在晶圆内部传播时受到吸收衰减，探测电路采集到的下表面反射回来的光强弱于上表面，因此，随着轴向位置的变化，信号峰值强度呈现先强后弱的变化趋势。

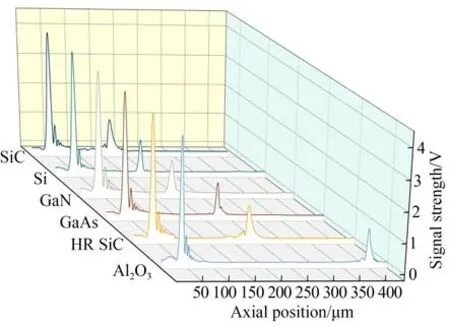
图13 激光共焦传感器的轴向响应曲线Fig.13 Axial response curve of laser confocal sensor

对每种晶圆进行10 次重复测量，通过光栅尺返回得到晶圆上下表面的光学位置坐标，经光线追迹换算出晶圆物理厚度，如图14 所示。表3 给出了每种晶圆样品的实际厚度平均值和测量重复性，可以看出，不同样品的厚度测量重复性均保持在100 nm 以内，实现了高精度检测。

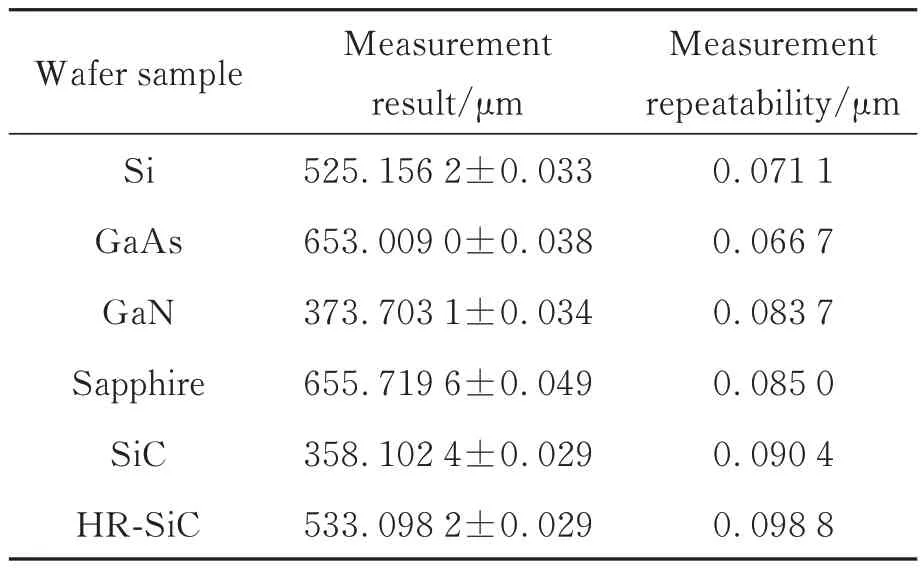
表3 晶圆厚度测量结果Tab.3 Results of wafer thickness measurement

图14 不同晶圆的测量结果曲线Fig.14 Curves of measurement results for different wafers

7 结论

本文提出了一种基于激光共焦原理的晶圆厚度高精度测量方法并完成了测量传感器构建，利用精密音圈纳米位移台实现共焦曲线峰值点的精确定位与轴向大范围扫描，测量范围达5.7 mm。实验结果表明，该技术的轴向分辨力优于5 nm。结合光线追迹方法实现晶圆内部物理坐标计算，对于不同种类的半导体晶圆，厚度测量重复性优于100 nm，检测时间优于400 ms。与现有的晶圆测厚方法相比，该方法在保证精度的情况下解决了晶圆检测中的高精度、无损直接测量等难题，实现了轴向高精度瞄准触发测量。激光共焦方法为半导体晶圆高精度检测设备的发展提供了一种新的技术途径。