改进型晶圆预对准算法

王石磊 李朋 陈胜华

宁波润华全芯微电子设备有限公司 浙江 宁波 315400

引言

随着半导体制程与良率的提升，对半导体制造工艺的需求也在不断升级，因此在晶圆处理环节对晶圆中心的定位精度在不断提高。在晶圆处理环节中，通常采用晶圆预对准系统对晶圆进行准确定位。晶圆预对准方式分为机械式预对准和光学式预对准[1]。早期半导体制造工艺中通常采用机械式晶圆预对准系统。这种方式构造简单、造价便宜，现在仍有一定的市场。但由于对准过程中采用直接接触，且受限于机械加工精度等客观原因；无论是采用下落式还是夹持式机械结构，都不克避免的会存在容易污染、损伤晶圆且精度不高的天然缺陷。因此采用逐渐被采用非接触式的光学式晶圆预对准系统取代。

1 光学式晶圆预对准系统

光学式晶圆预对准系统主要采用的是光学位置传感器对晶圆进行边缘扫描，通过对晶圆边缘进行非接触逐点采样，从而计算出晶圆中心坐标。光学式晶圆预对准系统通常根据轴数不同分为θ型、θ-X-Z型、θ-X-Y型[2]。以上几种形式的对准系统其θ轴通常采用图1示意图中所示结构进行晶圆圆心定位。

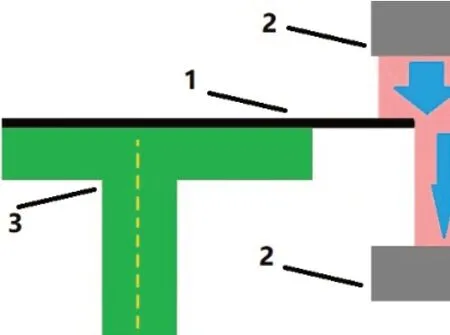
图1 光学式晶圆预对准系统示意图

图2 晶圆预对准系统单次采样数据

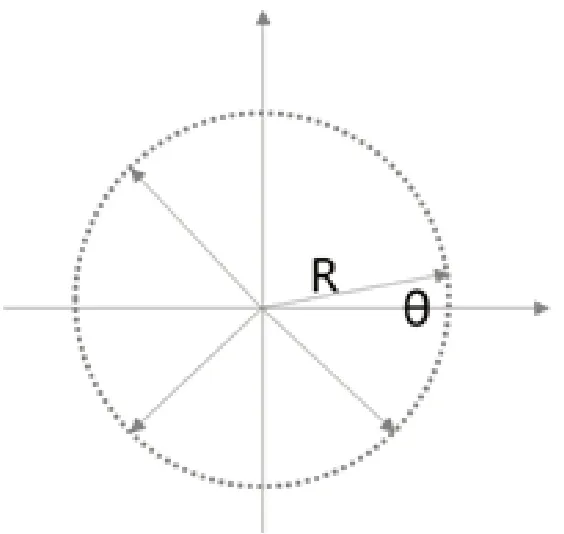
图3 直角坐标系数据

光学式晶圆预对准系统的工作过程可以简单描述为：承载台旋转，光学位置传感器获取不同旋转角度下晶圆边缘遮挡的长度，从而得到不同角度下晶圆边缘到旋转中心的半径。

得到采样数据后，其核心就是选择合适的算法计算出晶圆圆心坐标。传统的晶圆预对准算法有以下几种：回转半径法[3]、质心法[4]、圆最小二乘法等。其中回转半径法的测量条件要求比较苛刻，需要晶圆匀速旋转且采样频率精确，同时，需要把晶圆分为4的整数倍N，得到N个角度θ和距离r；从而求得晶圆圆心坐标：

质心法通过采样点划分扇形的方式对晶圆进行极坐标方向积分[5]：

其中，M为总质量，Mx为x轴方向的静矩，My为y轴方向的静矩。因此则有：

可得圆心坐标：

由于目前晶圆根据缺口类型主要分为两大类：Flat型（平槽）和Notch型（V平槽）[6]；其中Notch型晶圆一般尺寸较大，缺口本身相对较小，对计算得到的质心影响较小。但是Flat型缺口较大，因此质心法计算出的质心结果会与实际需要的晶圆圆心坐标形成一定误差。综上所述，质心法在适用性方面存在一定的局限性。

2 晶圆预对准算法改进

光学式晶圆预对准系统采集得到的极坐标系数据（Θi，Ri）（ i=1，2…N），其中Ri为晶圆边缘点到旋转中心的距离，Θi为晶圆旋转角度，N为总得采样次数。

通过坐标变换将极坐标数据转换到直角坐标系，得到直角坐标系下晶圆边缘采样点坐标（xi，yi）（ i=1，2…N）。

这里我们采样最小二乘法求解圆心坐标。设晶圆所在圆方程为：

其中，a、b、c为未知量，（x，y）为晶圆边缘上的点坐标。则：

其中，A=-a/2，B=-b/2，R=（a2+b2-4c）1/2/2。则可将问题转化为最小化问题，即已知坐标（xi，yi）（ i=1，2…N），最优的拟合圆为采样点到圆的距离最小。点（xi，yi）到拟合圆边缘的距离的平方与半径的平方差为：

令：

则此时求参数a、b、c使得F（a，b，c）值最小得到的圆心坐标即晶圆圆心。则分别对a、b、c求偏导，令偏导等于0：

根据Cramer’s Rule可得：

其中：

但通常由于以下因素的存在：

（1）晶圆本身存在缺口；

（2）晶圆加工过程中无法保证晶圆的绝对圆度；

（3）采样过程中各种因素的影响会在采样数据中引入误差。

因此，完全计入采样点会大量引入随机误差，导致计算得到的圆心坐标偏移，所以晶圆缺口采样点与部分误差较大采样点需剔除。

这里引入剔除系数λ（0＜λ＜1），在首次迭代确定圆心后，依次计算个点到圆心的距离，然后剔除距离最大的点；然后再次进行迭代。

进行n=[λN]次迭代后，晶圆缺口采样点与部分误差较大采样点会被剔除，但剩余的大部分采样点仍会存在一定测量误差。参考直线拟合中，Huber等人提出的权重函数的方法[7]。这里我们考虑为F（a，b，c）=增加权值ω以削弱距离圆心较远点的权重。则F（a，b，c）=Σ可表述为：

为了降低离圆心距离较远点的权重，这里取：

τ为削波系数：

即削波系数取决于所有采样点到圆心距离的中位数。

3 实验验证

在圆心坐标为（1.000，0.000）半径15.00的圆上提取40组坐标点，然后在其中5组坐标数据中增加随机误差，构成5组偏离圆的干扰点坐标。这样一共形成40组坐标点作为测试数据：

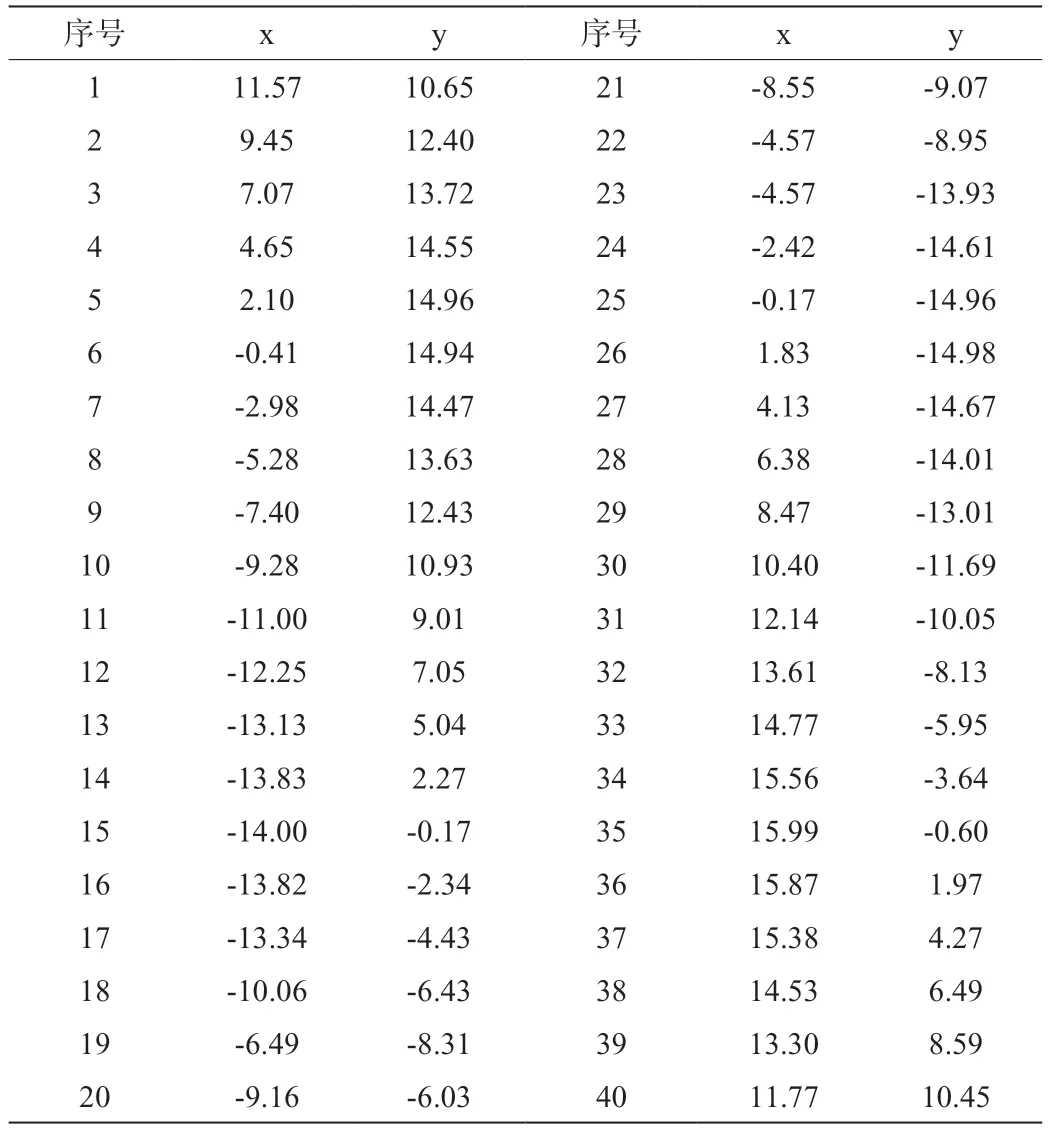
表1 测试采样点数据

这样分别采用直接进行最小二乘法拟合的计算方法和采用剔除并加权的优化后圆心计算方法，分别带入上述40组采样数据，对晶圆圆心坐标进行计算。可以得到优化前后两种算法计算得到的圆心坐标差异。并将计算结果绘制得到图4。

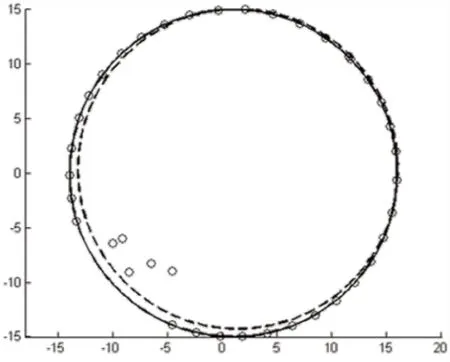
图4 数据剔除并加权前后拟合结果对比

在图4中，可以看到剔除并加权前后拟合结果对比（虚线为直接采样最小二乘法圆拟合效果，实线为剔除并加权后拟合效果，空心圆点为采样数据）。

图5为局部结果图像的放大部分，可以看到采用剔除并加权的算法后，计算得到的圆能有效排除干扰点的影响，能更多地通过采样坐标点。

图5 拟合结果对比局部放大

可分别求得剔除干扰数据并加权前的圆心坐标为（1.411，0.381）；剔除干扰数据并添加权重后的圆心坐标为（0.999，0.0005）。因此采用剔除干扰数据并增加权重系数可有效提升晶圆圆心的计算精度。

4 结论

本文针对光学位置传感器晶圆预对准系统中，传统方法无法有效排除异常采样数据的问题，提出了采用剔除采样干扰点并引入权重的方法。通过仿真实验验证，采用新的圆拟合算法，可有效提升晶圆预对准系统的定位精度。