过渡区内纳米颗粒的曳力特性模拟研究*

刘旺旺 张克学 王军 夏国栋

(北京工业大学,传热强化与过程节能教育部重点实验室,传热与能源利用北京重点实验室,北京 100124)

在过渡区内,关于纳米颗粒曳力计算及输运特性的研究较为困难,通常会采用一些近似方法,将自由分子区或者连续介质区的理论计算式进行修正,以适用于过渡区,但是其准确性值得商榷.本文基于分子动力学模拟方法,研究了过渡区内纳米颗粒的曳力特性,并与相关理论进行对比.结果表明,气-固分子间相互作用对纳米颗粒的曳力具有显著影响.当气固结合强度较弱时,理论计算结果与分子动力学模拟值吻合较好;当气固结合强度较强时,分子动力学模拟结果明显大于理论值,这是由于气体分子在纳米颗粒表面的吸附所导致.基于气体分子在颗粒表面的吸附特性,提出引入有效颗粒半径修正,其过渡区内曳力的理论计算结果与分子动力学模拟结果吻合较好.

1 引言

当颗粒以一定的相对速度在气体中运动时,气体会阻碍颗粒的运动,这个阻碍颗粒运动的力被称为曳力[1-3].关于颗粒曳力特性的研究在很多领域都有重要意义,例如气溶胶科学、环境科学、燃烧学、纳米材料合成以及核安全等[4-11].曳力通常被认为是悬浮颗粒在流体中受到的最主要的作用力,根据Stokes-Einstein 输运理论,颗粒的布朗扩散系数与其曳力系数成反比.近年来,关于纳米颗粒在气体中曳力计算及输运特性的研究引起了广泛的关注[12-18].

悬浮颗粒在气体中的受力及其输运特性与Knudsen 数密切相关.Knudsen 数定义为气体分子平均自由程λ 与颗粒半径R的比值,Kn=λ/R.根据Knudsen 数的大小,可将颗粒的动力学行为划分为自由分子区(Kn≫1)、连续介质区(Kn≪1)和过渡区(Kn～1).在自由分子区,气体分子平均自由程远大于颗粒半径,因此可忽略被颗粒反射的气体分子与其他入射分子之间的碰撞,即不考虑颗粒的存在对气体分子速度分布函数的影响.基于气体动理论方法,Epstein[19]推导了自由分子区内球形颗粒的曳力.在连续介质区,气体分子之间的碰撞频率远大于气体分子与颗粒之间的碰撞频率,因此,气体介质可视为连续流体.Stokes[20]提出了球形颗粒在连续介质区内曳力的表达式.在过渡区,气体分子间的碰撞频率和颗粒与气体分子之间的碰撞频率相当,连续介质假设不再适用,自由分子区的处理方法同样也不再适用,因此对曳力的求解比较困难.通常会采用一些近似方法建立理论模型,如矩方法和Bhatnagar-Gross-Krook 方法等,但其准确性值得商榷[21].通过引入修正系数,可以将连续介质区或者自由分子区的理论结果拓展,以适用于过渡区,例如Stokes-Cunningham 曳力修正公式[22]:

式中,μ为气体的黏度,V为颗粒相对于气体的速度,A,B,E为经验参数.实际中常采用A=1.155,B=0.471,E=0.596[23].

上述理论均基于气体分子与颗粒之间的刚体碰撞假设建立模型,此假设对于微米量级的大颗粒来说是适用的,但是当颗粒的尺寸逐渐降低到亚微米或纳米量级时,刚体碰撞模型可能不再适用[24-26].此时需要考虑气体分子与颗粒之间的非刚体碰撞效应,例如范德瓦耳斯力等[27-29].纳米颗粒与气体分子之间的非刚体相互作用会使气体分子的运动轨迹发生偏转,从而影响碰撞过程中的动量传递,最终影响颗粒的受力特性.Li 和Wang[30]基于气体动理论和非刚体碰撞模型,得到自由分子区内纳米颗粒所受的曳力表达式,并采用半经验的处理提出了过渡区内纳米颗粒的曳力表达式[31]:

式中,w是由实验数据得到的拟合值,取为1.143[31],mr是约化质量,kB是玻尔兹曼常数,T是系统温度,n是气体数密度,是无量纲碰撞积分项.但是,(2)式的准确性尚未得到验证.

基于分子动力学(molecular dynamics,MD)模拟方法,研究了过渡区内纳米颗粒的曳力特性.研究发现,对于纳米颗粒而言,模拟结果与(2)式并不相符.气固结合强度对纳米颗粒的曳力有显著影响,当结合强度较强时,需要考虑气体分子在颗粒表面的吸附效应.使用修正的有效颗粒半径后计算(2)式的结果与分子动力学模拟结果吻合良好.

2 分子动力学模拟计算

2.1 分子动力学模型

本文采用分子动力学模拟方法计算纳米颗粒在过渡区内所受的曳力.分子动力学模型如图1 所示,纳米颗粒悬浮于一定量的气体分子中,其中纳米颗粒由NS个铜原子组成,气体分子由NF个氩原子组成.模拟系统在x,y,z方向上的长度分别为Lx=270 Å,Ly=80 Å,Lz=80 Å (1 Å=10-10m),3 个方向均采用周期性边界条件.在本文的模拟系统中,对铜原子之间的相互作用采用嵌入原子法(embedded atomic method,EAM)势能[32]:

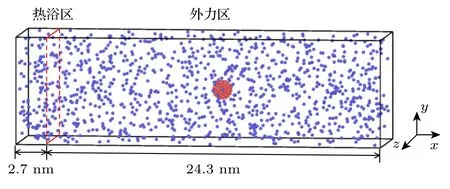
图1 分子动力学模拟系统模型图(红色: 纳米颗粒;蓝色: 气体分子)Fig.1.Configuration of MD simulation system (Red: nanoparticle;blue: gas molecules).

其中Ei,ρi,re分别代表嵌入能量、原子电子密度、最近邻之间的平衡间距,P,ξ,Q,ψ 是4 个可调参数,ω 和τ 是两个额外的截止参数.对气-气和气-固原子之间的相互作用采用经典的Lennard-Jones(LJ 12-6)势能函数:

其中,ε 表示LJ 势阱深度,σ 是势能为零时的距离,rij为原子i和j之间的距离.气体与固体原子之间势能参数的选取,遵循Lorentz-Berthelot 混合原则:

表1 列出了LJ 势能函数的参数[33].本文通过改变气-固分子之间势函数的能量参数来改变气固界面的结合强度:

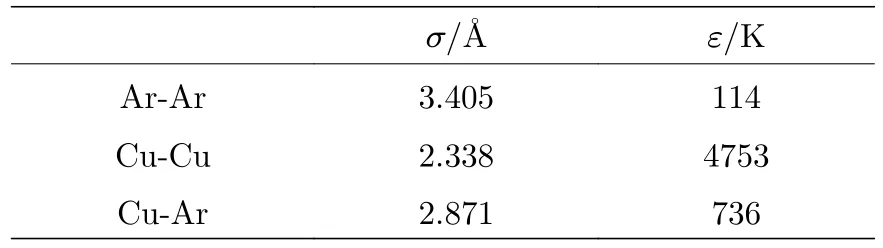
表1 LJ 势函数参数值[33]Table 1.LJ potential parameters[33].

本文使用LAMMPS (large-scale atomic/molecular massively parallel simulator)开源软件进行分子动力学模拟计算[34].在模拟过程中,时间步长取为2 fs,截断半径rc=0.9 nm.在弛豫阶段,系统首先在NVT 系综下运行3 ns,使用Nosè-Hoover 热浴使得系统的温度保持在180 K.然后将模拟系统在x方向分为两个区域,左端长度为2.7 nm 的区域设定为热浴区,右端长度为24.3 nm 的区域设定为外力区,如图1 所示.在热浴区施加NVT 系综使其维持在180 K,在外力区域给每个气体分子添加一个外力,5 ns 后系统内可以形成恒定的流速.最后在NVE 系综下运行120 ns并计算相关物理量.基于遍历原理,本文所给出的任何物理量都是在采样时间范围进行的长时间平均得到的.为了提高计算结果的准确性,本文采用不同初始微观条件(即原子初始速度不同,但需满足同一个Maxwell 速度分布律)下至少8 次独立运行结果的算数平均值作为最终计算结果.

2.2 计算方法

对于悬浮在气体中的纳米颗粒,其布朗运动会给曳力的计算带来较大的困难.因此,本文在纳米颗粒上施加了一个额外的简谐回复势能Uhar[35-37]:

式中,khar表示简谐势能的弹性系数,xc和xo分别表示纳米颗粒的质心位置和初始位置.当系统达到稳定后,纳米颗粒所受的曳力与简谐力平衡,纳米颗粒相对于它的初始位置会具有一个相对位移Δx,此时,纳米颗粒所受的曳力FD可以通过下式计算:

为研究外加简谐势弹性系数对纳米颗粒所受曳力的影响,计算了曳力随弹性系数khar的变化情况.图2 计算结果表明,弹性系数的大小对纳米颗粒的曳力计算结果几乎没有影响,这是由于本文采用的曳力计算方法是基于颗粒所受曳力与简谐回复力之间的平衡.当弹性系数khar增大时,相对距离Δx会相应减小,但是二者的乘积基本保持不变.因此,曳力不会受到弹性系数khar的影响,而是依赖于颗粒与流体的物性及它们之间的相互作用.文献[38]的研究结果表明,只要khar＞0.1εF/,弹性系数对统计结果不会产生影响,这与本文的结论一致.本文选取khar=30εF/.

图2 纳米颗粒的曳力随弹性系数khar 的变化Fig.2.Drag force on nanoparticles versus elastic coefficient khar.

本文采用Green-Kubo 公式对气体黏度进行计算[39]:

式中,V为模拟盒子的体积,〈···〉为系综平均值,Jγν为γν应力张量的分量 (γν=xy,xz,yz),N,m,v分别为气体分子的数量、质量、速度.

球形纳米颗粒的半径可使用下式进行计算[40]:

式中,xj为固体原子j的坐标.

3 纳米颗粒的曳力计算

3.1 纳米颗粒的有效粒径

在过渡区内,纳米颗粒的曳力受Knudsen 数的影响较大.通过选取适当的气体分子数来改变系统的Knudsen 数,使得模拟区域处于过渡区内.图3 显示了3 种气固结合强度下曳力随着Kn的变化.可以看到,纳米颗粒的曳力随着Kn而逐渐降低.这是由于当Kn增大时,气体分子数逐渐减少,气体分子与颗粒之间的碰撞频率逐渐降低,气固之间的动量传递随之减弱,因而纳米颗粒受到的曳力逐渐减小.此外,当气固结合强度较大时,气体分子与颗粒之间的相互作用较强,气固之间的动量传递较强,因而颗粒会受到更大的曳力.

图3 MD 模拟值与理论公式在3 种气固结合强度下的对比结果 (a) kSF=0.01;(b) kSF=0.1;(c) kSF=0.5Fig.3.Comparison of MD simulation results of the drag force with theoretical values at various kSF: (a) kSF=0.01;(b) kSF=0.1;(c) kSF=0.5.

为了便于将模拟结果与理论公式进行比较,将(1)式和(2)式的计算结果也绘制在图3 中.当kSF=0.01 时,气体分子与纳米颗粒之间的碰撞过程近似于刚体碰撞,此时MD 模拟结果与(1)式和(2)式的结果均吻合良好.当kSF=0.1 和kSF=0.5 时,气体分子与纳米颗粒之间的非刚体碰撞效应不可忽略,相比于(1)式,MD 模拟值更接近于(2)式的结果,这表明考虑气-固间非刚体相互作用的(2)式对纳米颗粒的曳力具有更好的预测.此外,当kSF=0.1 时,MD 模拟结果略大于(2)式的预测值,而当kSF=0.5 时,MD 模拟结果明显大于(2)式的结果(见空心圆点).由于气体分子与纳米颗粒之间的相互作用,气体分子通常会被吸附在颗粒表面,并在颗粒表面随机行走,当气体分子获得足够多的能量后,就会从颗粒表面离开,在颗粒表面达到一个吸附与脱附的动态平衡[41,42],如图4 所示.此外,气体分子在颗粒表面的吸附特性可由一个无量纲参数来表征,即/(kBT),其中=kSFεSF.该比率体现了气固结合能与气体分子动能之间的相对大小[42-44].当/(kBT) 较小时,气固结合能低于气体分子的动能,气体分子容易克服界面势垒而脱附.当/(kBT)逐渐增大时,气固之间的结合能逐渐增大或者气体分子的动能逐渐降低,因而大量气体分子被吸附于颗粒表面.图4 展示了4 种kSF下气体分子在纳米颗粒表面吸附的模拟快照.当kSF=0.01 时,/(kBT)≪1,几乎没有气体分子能被吸附在颗粒表面,如图4(a)所示,此时气体分子与颗粒之间的相互作用接近于刚体碰撞,因此MD 模拟结果与(1)式及(2)式的预测吻合良好;当kSF=0.1 时,/(kBT)略小于1,部分气体分子可吸附在颗粒表面,见图4(b);当kSF=0.5 时,/(kBT)＞1,大量气体分子被吸附,并在颗粒表面形成一个吸附层,见图4(c);当kSF=2.0 时,/(kBT)≫1,颗粒表面吸附达到饱和.这个吸附层会增大颗粒的尺寸,并增大了气体分子与颗粒之间的碰撞面积,更有利于二者之间的动量传递,从而增大了纳米颗粒所受的曳力.因此,当kSF=0.1 和kSF=0.5 时,MD 模拟值会大于(2)式的预测结果.

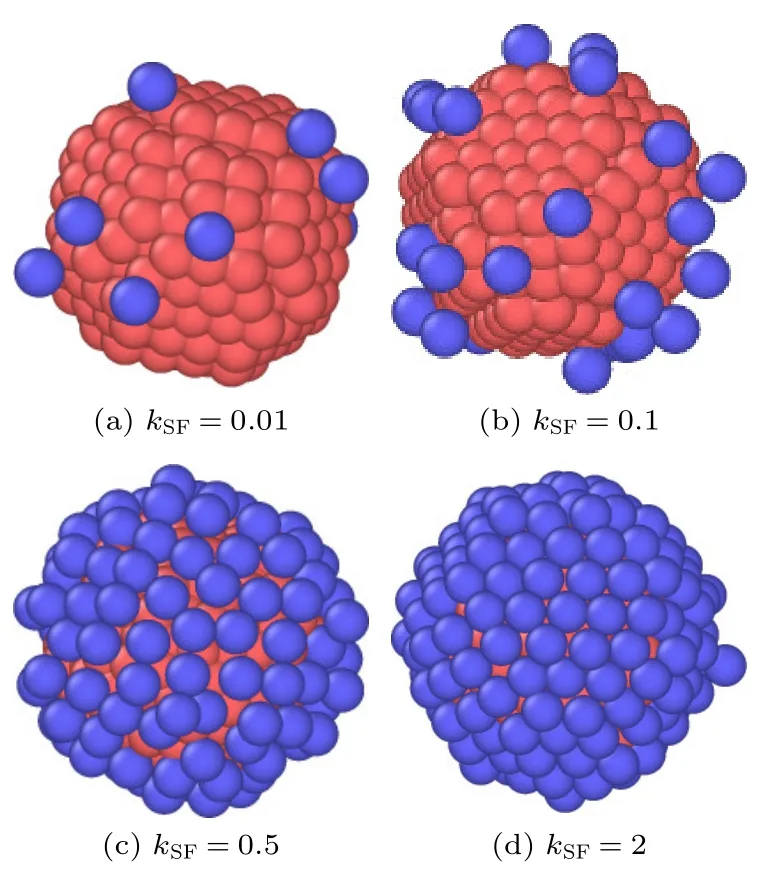
图4 气体分子在纳米颗粒表面吸附状况的模拟快照Fig.4.Snapshots of the adsorption of gas molecules (blue)on the nanoparticle (red) surface.

考虑到气体分子在颗粒表面的吸附效应,本文提出需要引入有效颗粒半径对(2)式进行修正.为了计算有效颗粒半径,首先需要评估吸附层厚度.吸附层厚度与界面处气体分子的分布情况紧密相关.当kSF较小时,颗粒表面吸附的气体分子较少,其等效的吸附层厚度较小;kSF逐渐增大时,颗粒表面吸附的气体分子增多,吸附层厚度增大,颗粒的有效半径增大.本文引入一个吸附参数α 来表征纳米颗粒表面气体分子的吸附强弱,α(kSF)=Na(kSF)/Nm,其中Na(kSF) 为各种kSF下吸附的气体分子数,Nm为kSF=2 时的吸附气体分子数.图5 展示了吸附率α 随kSF的变化情况.可以看到,吸附率α 随着kSF而逐渐增大,并在kSF较大时逐渐趋于定值.当气固结合强度较弱时,只有很少的气体分子会被吸附在颗粒表面,因而随着气固结合强度的增强,吸附参数增大较快.对于较强的气固结合强度,由于纳米颗粒表面已经吸附了较多的气体分子并覆盖在颗粒表面,入射气体分子难以与纳米颗粒发生相互作用,而更可能与已被吸附的气体分子发生碰撞,此时入射气体分子不容易被颗粒吸附.

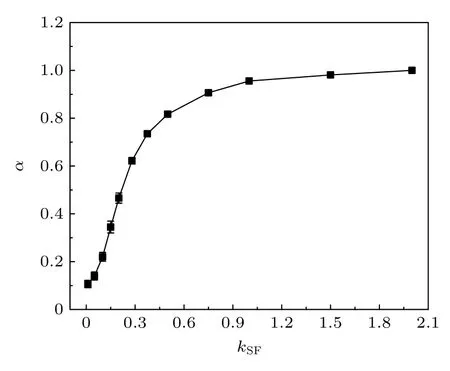
图5 吸附率α 随气固结合强度kSF 的变化Fig.5.Adsorption ratio α versus gas-particle coupling parameters kSF.

吸附率α 可表示各种kSF下的吸附层厚度与颗粒表面被完全覆盖时吸附层厚度的比值,吸附层厚度与原始颗粒半径之和即为有效颗粒半径.有效颗粒半径可以近似基于下式计算:

式中,δ 是界面吸附层的有效厚度,δm是当kSF=2 时的吸附层厚度.kSF=2 时的吸附层厚度可以在图4 中得到.考虑到气体分子在纳米颗粒表面的吸附对Knudsen 数的计算也会有影响,因此本文对Kn也进行了修正,Kne=λ/Re.把修正后的有效半径Re和Knudsen 数Kne代入(2)式中,将计算的曳力值重新绘制在图3 中(见实心圆点).可以看到,修正后的理论公式结果与MD 模拟值非常吻合.

3.2 颗粒尺寸对纳米颗粒曳力的影响

纳米颗粒所受曳力与其颗粒尺寸有关,本文通过改变固体原子数来改变纳米颗粒的大小.固体原子数分别选取NS=141,225,369,555,767 和1061,根据(13)式可计算出对应颗粒半径R分别为0.724,0.869,1.014,1.158,1.303 和1.448 nm.同时,气体分子数密度维持在1.97 nm-3,以确保流动区域处于过渡区.图6 展示了当kSF=0.01,0.1 和0.5 时纳米颗粒的曳力随着颗粒半径的变化图,其中气体流速维持在大约1.5 m/s.结果表明,纳米颗粒的曳力随颗粒半径的增大而增大.这是由于当颗粒半径增大时,其表面积也会随之越大,气体分子更容易与颗粒发生碰撞,从而促进了气体分子与纳米颗粒之间的动量传递,因此颗粒会受到更大的曳力.此外,为了便于与理论公式进行比较,(2)式的计算值也被绘制在图6 中.可以看到,当kSF=0.01 时,MD 模拟结果与(2)式的预测值相当吻合,然而当kSF=0.1 和kSF=0.5 时,MD 模拟结果则大于(2)式的计算结果.如上所述,当气固结合强度较大时,气体分子在颗粒表面的吸附作用不容忽视,需要对颗粒半径进行修正.根据(14)式可得到修正的有效颗粒半径,代入(2)式重新计算了曳力,并绘制于图6 中(见蓝色点线).由图6 可知,此时考虑颗粒粒径修正之后的计算结果与MD 模拟值更加吻合.

图6 MD 模拟值与(2)式在3 种气固结合强度下的对比结果Fig.6.Comparison of MD simulation results of the drag force with Eq.(2) at various kSF.

3.3 气体流速对纳米颗粒曳力的影响

气体流速也是影响纳米颗粒所受曳力的重要因素之一.在本文的模拟中,通过调整外力区域内施加在每个气体分子上的外力从而形成不同的气体流速.图7 展示了在3 种气固结合强度下曳力随着气体流速的变化图.结果表明,纳米颗粒的曳力随着气体流速而增大.当气体流速增大时,气体分子与颗粒的碰撞更加剧烈,加强了二者之间的动量传递,因而颗粒具有更大的曳力.此外,(2)式也被绘制在图7 中并与MD 模拟值进行对比.当kSF=0.01 时,气体分子难以吸附在颗粒表面,MD 模拟值能与(2)式的结果良好吻合.而当kSF=0.1 和kSF=0.5 时,气体分子与纳米颗粒之间的相互作用较强,气体分子容易被吸附在颗粒表面,并增大了纳米颗粒的半径,使得MD 模拟值大于(2)式的预测值,这与上文结论一致.考虑到气体分子的吸附,需要采用修正的有效颗粒半径.在过渡区,由于气体分子比较稀薄,可以忽略流速对气体分子吸附效应的影响.根据(14)式可计算得到有效颗粒半径,代入(2)式并将计算结果绘制在图7 中(见蓝色点线).不难看出,修正后的(2)式与MD 模拟结果吻合更好.

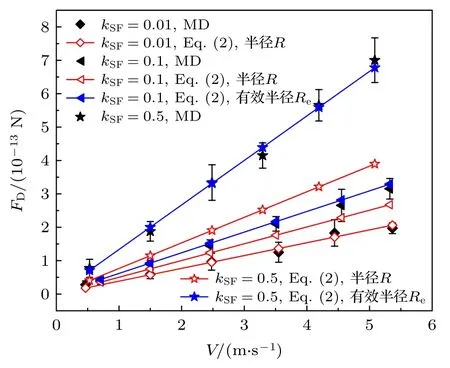
图7 MD 模拟值与(2)式在三种气固结合强度下的对比结果Fig.7.Comparison of MD simulation results of the drag force with Eq.(2) at various kSF.

4 结论

本文基于分子动力学模拟方法,计算了过渡区内纳米颗粒所受的曳力,并与Li 和Wang[31]提出的纳米颗粒曳力计算式进行对比.结果表明,对于纳米颗粒而言,当气固结合强度较弱时,分子动力学模拟结果可以与理论计算结果吻合较好;当气固结合强度较强时,分子动力学模拟结果明显大于理论计算的结果.进一步分析表明,此差异是由气体分子在纳米颗粒表面的吸附行为所导致的.本文基于气体分子在颗粒表面的吸附特性,提出引入有效颗粒半径修正,其过渡区内曳力的理论计算结果与分子动力学模拟结果可以更好地吻合.因此,对于纳米颗粒而言,气体分子在颗粒表面的吸附效应不可忽略.