非线性声场下包膜微泡动力学与频率响应分析*

索鼎杰 纪镇祥 黄晓雲 靳杰 闫天翼†

1) (北京理工大学医学技术学院,北京 100081)

2) (北京理工大学前沿交叉科学研究院,北京 100081)

包膜微泡在非线性声场下的响应对高强度聚焦超声治疗具有重要意义.本文通过耦合Gilmore-Akulichev-Zener 模型与脂质包膜的非线性模型,采用KZK 方程仿真非线性声场,分析在不同超声频率、不同声压以及不同包膜材料的黏弹性下的微泡动力学行为和微泡振荡频率,并进一步对比了实际测量声场与KZK 方程仿真声场下的微泡动力学行为和频率响应.研究结果表明: 非线性声场会导致微泡壁的瞬时运动速率减小,声压和频率的改变对微泡动力学的影响与在线性声场中类似;包膜材料的不同可以使振荡频率中的谐波分量发生改变,其中包膜材料的弹性对微泡的频率响应影响较小,包膜的初始黏性和初始表面张力对微泡的振荡频率分布影响较大,当初始黏性越小时,二次分谐波的峰值越高,当初始表面张力越大时,主频的峰值越高.本研究进一步阐明非线性超声激励包膜微泡的微泡动力学,为包膜微泡在非线性声场下的频率响应分析奠定理论基础.

1 引言

声空化[1-3]是指超声波与传播介质中的气核之间的相互作用,在负声压的作用下使介质中气核迅速扩张,出现空腔的现象;声空化分为稳态空化和瞬态空化.稳态空化[4,5]是指气泡稳定的振荡,存在的时间较长,可用于聚焦超声诱导的血脑屏障开放,通过调节稳态空化,可以降低脑损伤的风险,提高药物的靶向递送率;瞬态空化[6,7]是指声压达到惯性空化阈值后,气泡剧烈的振荡,存在的时间较短,瞬态空化可以产生冲击波和微射流,可用于聚焦超声组织摧毁[8,9]、血栓消融[10,11]、肿瘤治疗[12,13]等.此外,空化效应还可能导致光学效应(声致发光)[14,15]、化学效应[16,17]和其他热效应[18,19].因此,对声空化进行研究十分重要.

近年来,许多研究人员对单个微泡在超声激励下的动力学模型进行了研究和修正.Rayleigh-Plesset (RP)[20]方程通过将液体视为不可压缩流体被广泛运用于计算微泡动力学的基础.Keller和Miksis[21]通过拓展RP 方程,将液体视为轻微可压缩流体,使得方程在大气泡和大振幅下更加适用.Doinikov[22]通过拓展Keller 和Miksis[21]的研究,将气泡的平移运动方程和径向运动方程进行耦合,研究了气泡平移运动对微泡动力学的影响,随后通过研究次级Bjerknes 力[23]和声学流线的特性,表明次级Bjerknes 力对气泡之间的相互作用起到了重要的作用,并且声学流线的形成与次级Bjerknes 力密切相关,目前该模型已被广泛应用.Yang 和Church[24]通过耦合Keller-Miksis (KM)方程与Kelvin-Voigt 方程,研究了软组织中的声空化阈值[25].Zilonova 等[26]通过耦合Gilmore-Akulichev 方程与Zener 黏弹性模型,使得方程在高马赫数的情况下适用,并研究了高强度聚焦超声在组织中的声空化阈值.

为了降低声空化阈值,通常使用微米涂层脂质包膜泡作为造影剂来提高空化治疗时的安全性、稳定性和可控性.影响脂质包膜微泡声空化的主要因素包括: 膜的黏性、膜的弹性、膜的初始表面张力等.Marmottant 等[27,28]提出了单个超声造影剂气泡的模型,该模型考虑了气体微气泡上脂质包膜的物理特性,目前已被广泛地应用.于洁等[29]在此基础上对脂质包膜材料的黏性参数进行了非线性修正,使得模型的应用更加广泛.秦对等[30]通过耦合Gilmore-Akulichev-Zener (GAZ)模型与脂类包膜的非线性黏弹性模型,研究了微泡的声空化动力学行为以及微泡周围组织内机械应力.上述研究基本都是在线性波的驱动下进行数值分析,然而,高强度聚焦超声在传播时,会出现衍射、散射、衰减以及声吸收的情况,导致波形畸变和谐波,产生非线性.通常用于模拟聚焦换能器发射超声波的两种常用非线性模型分别是KZK (Khokhlov-Zabolotskaya-Kuznetsov)[31]方程和Westervelt[32]方程.2019 年,Bakhtiari-Nejad 和Shahab[33]通过求解KZK 方程的数值解耦合KM 方程,研究了气泡在非线性声场下的径向运动和平移运动.

本文主要采用KZK 方程进行高强度聚焦声场仿真,耦合GAZ 方程与包膜的黏弹性模型,采用步长控制算法和Runge-Kutta5 (RK5)算法,探讨在非线性声场中不同超声频率、不同声压以及不同包膜材料的黏弹性下的微泡动力学行为和微泡振荡频率响应,进一步分析不同超声参数和包膜材料对微泡振荡频率中谐波分量的影响,最后采用实际测量的非线性声场数据与KZK 方程仿真的声场数据进行对比,探究实际声场和仿真声场之间的差异.

2 理论模型

2.1 GAZ 模型

在数值仿真中,由于高强度聚焦超声会导致微泡的大幅度振荡,气泡壁的运动速度高于1 Mach(1 Mach=340.3 m/s),GA 模型更适用高马赫环境,并且Zener[26]模型相比于Kelvin-Voigt 模型能更好地适用于黏弹性组织,能较好地模拟微泡的径向应力,因此本研究采用GAZ 模型:

其中,c0是流体中的声速,R0是初始半径,H是气泡壁的焓变,µ是介质中的黏性,p0是静态压力,σ0是初始表面张力,ρ是组织密度,B和n是常数.B=-p0,p1是微泡内部的压力,p是驱动声压,τrr|R是径向应力,φ是组织的松弛时间,且q=.

2.2 包膜的非线性黏弹模型

包膜材料能提高微泡的稳定性,其黏弹特性能够减小气泡的压缩和扩张.非线性修正的Kelvin-Voigt[28,29]模型能够较好地考虑包膜微泡的黏弹性[34,35]:

其中,S1为包膜弹性项,S2为黏性项,且包膜表面张力σ(R) 的径向变化如下:

其中,Rb为微泡半径最小值,且Rb=,当R≤Rb时,微泡发生皱缩,Rr为微泡破裂半径,且Rr=,且σr=σ0,当R≥Rr时,微泡发生破裂.其中k表示包膜微泡的黏度,λ为包膜微泡的弹性,且k=,k0为壳的初始黏性参数,α为特征时间常数.

2.3 驱动声压和数值条件

驱动声压采用KZK 方程的模拟,通过HIFUSimulator (Food and Drug Administration,Silver Spring,MD)[36]进行仿真:

其中p是在介质中的声压,z是轴向坐标(垂直于换能器表面),x和y为横向坐标(平行于换能器表面),且延迟时间τ=t-z/c0,β为非线性系数,b为耗散系数.通过频域的傅里叶级数解法展开可得

其中Cn为第n次谐波的振幅[37].

假设微泡内部的压力服从范德瓦耳斯方程[38],则可以采用下式表示:

其中,h=R0/8.4 是微泡的范德瓦耳斯半径,γ是多向性系数.

表1 参数名称和值Table 1.Name and value of the parameters.

3 仿真结果分析与讨论

3.1 非线性超声的响应

超声波在传播过程中会出现衍射、散射、衰减现象,从而产生波形畸变,采用KZK 方程模拟超声波在水中的非线性传播.图1 对比了线性超声和非线性超声在相同正压下的微泡径向运动行为和振荡频率响应(其中线性声场采用驱动声压为:P=-Ptsin(2πft),Pt为振幅,f=1 MHz),初始半径R0=1 μm,声压P=2.0 MPa.对比线性声场和非线性声场下的微泡动力学行为,可以发现超声波传播时的损耗导致负压偏小,从而使得微泡的径向运动减弱,气泡壁的运动速度也相应减小,微泡的振荡频率峰值也随之减小.图2 对比了非线性声场下不同声压和不同频率下的微泡动力学行为和频率响应,初始半径R0=1 μm,当频率固定在f=1.0 MHz,声压增大时,微泡的径向运动显著增强,从而使得振荡响应频率的峰值也增大.当声压固定在2.0 MPa 时,频率增大时,微泡的径向运动却开始减小,这是由于微泡的振荡主频峰值减小和远离共振频率导致的.

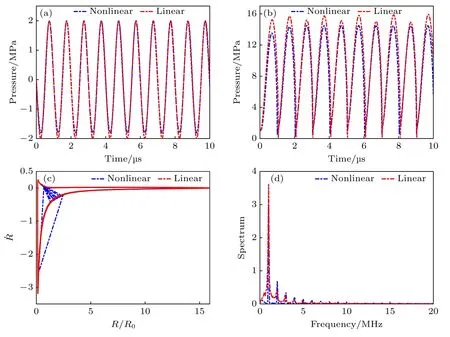
图1 线性声场和非线性声场下微泡动力学行为频率响应 (a) 相同正压下的线性超声与非线性超声波形图;(b),(c) 微泡动力学行为的对比;(d) 微泡半径变化的振荡频率响应,蓝色线条表示驱动声压为KZK 方程仿真的非线性声场,红色线条表示线性声场Fig.1.Dynamics behavior and frequency response of microbubbles under linear and nonlinear ultrasound fields: (a) Linear and nonlinear ultrasonic waveforms under the same positive pressure;(b),(c) comparison of bubble dynamics behaviors;(d) oscillation frequency response of the microbubble radius change,the blue lines represent the driving sound pressure as the nonlinear ultrasound field simulated by the KZK equation,and the red lines represent the linear ultrasound field.

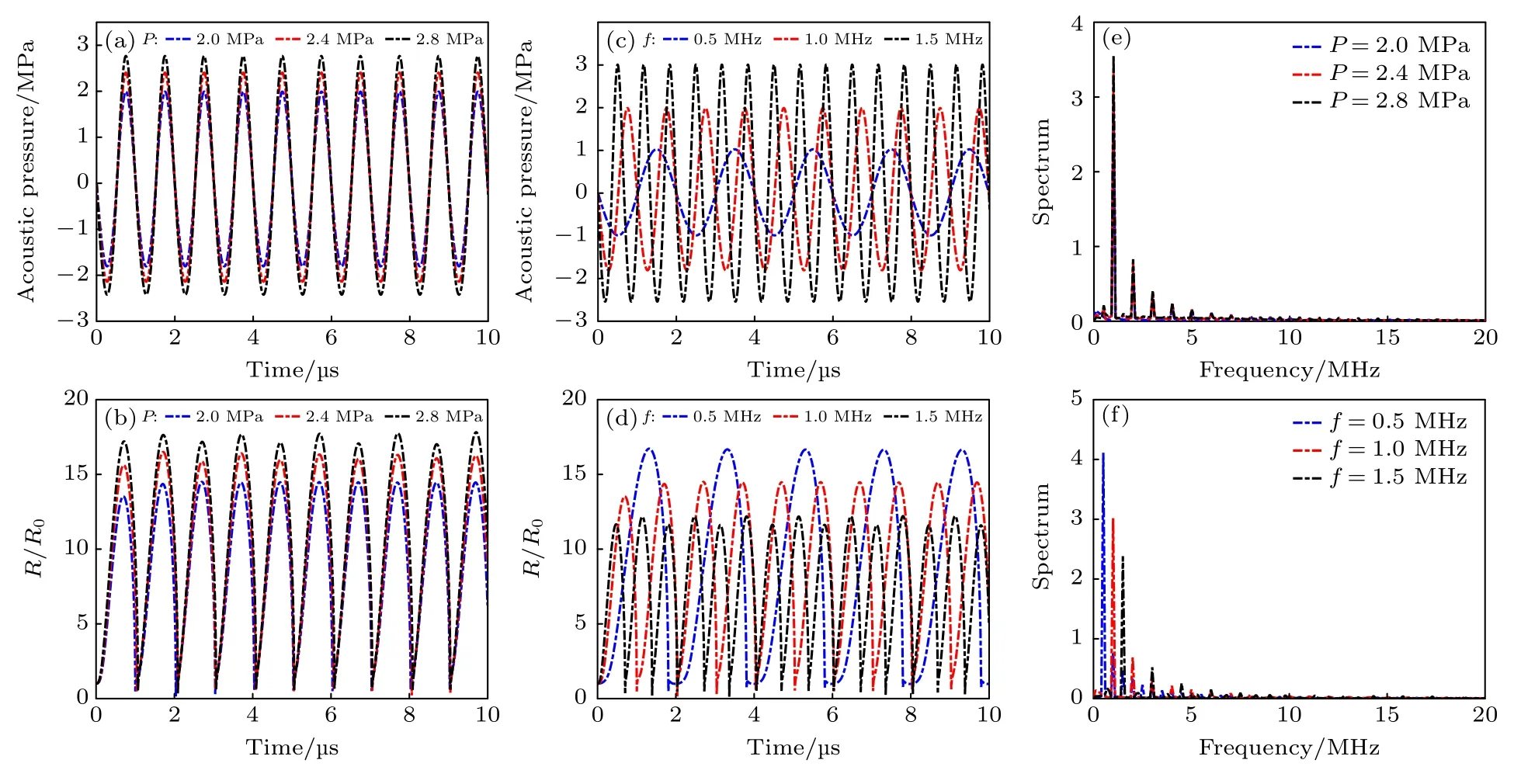
图2 (a),(b),(e) 不同声压下非线性超声的微泡动力学行为和频率响应的差异;(c),(d),(f) 不同频率下非线性超声的微泡动力学行为和频率响应差异Fig.2.(a),(b),(e) Differences in the kinetic behavior and frequency response of microbubbles in nonlinear ultrasound at different acoustic pressures;(c),(d),(f) differences in microbubble kinetic behavior and frequency response of microbubbles in nonlinear ultrasound at different frequencies.

3.2 脂质包膜参数影响

图3 对比了不同脂质包膜微泡的初始表面张力和初始黏性参数对微泡动力学行为和频率响应的影响,初始条件设置如下:f=1 MHz,P=2.0 MPa,R0=1 μm.可以发现当膜的初始表面张力较大时,微泡的径向运动增强,频率响应中谐波的数量增加;当包膜的初始黏性减小时,微泡的径向运动更加剧烈,频率响应中二次分谐波的峰值升高.为了探究包膜材料对频率响应的影响,采用同样标准来判断,即C=(P11max1表示最大响应频率fmax1对于的频谱值,P11max2表示第二响应频率fmax2对于的频谱值),若|C|越大,则微泡的频谱峰值更高,若小于C＜0 且|C|越小,则表示分谐波得到了增强,若C＞0 且|C|越小,则表示次谐波得到了增强.图4 对比了不同包膜参数对微泡动力学行为和频率响应的影响,仿真条件都是:f=1 MHz,P=2.0 MPa,R0=1 μm.图4(a),(b)分别表示包膜微泡的初始表面张力σ0在0—0.07 N/m 和弹性λ在0—1 N/m 时微泡动力学行为和频率响应.可以发现包膜微泡的初始表面张力越大,微泡的径向运动越剧烈,分谐波的频率响应越大,但包膜微泡的弹性对微泡动力学行为和频率响应几乎没有影响.图4(c),(d)分别表示包膜的初始黏性k0在0.5×10-8—1.0×10-7kg/s 和初始弹性λ在0—1 N/m 时微泡动力学行为和频率响应.可以发现当脂质包膜的初始黏性增大时,微泡的径向运动减小,频率响应中超谐波的分量增强;当包膜的初始黏性减小时,微泡的径向运动增强,频率响应也提高了分谐波的分量.图4(e),(f)分别表示包膜的初始黏性k0在0.5×10-8—1.0×10-7kg/s和包膜微泡的初始表面张力σ0在0—0.07 mN/m时的微泡动力学行为和频率响应,可以发现当包膜的初始黏性和初始表面张力一起改变时(包膜的初始黏性小且包膜微泡的初始表面张力越大),微泡振荡的主频和次谐波分量的峰值变高,因此在进行聚焦超声消融时,可以通过改变脂质微泡的包膜材料,进一步调节信号的频率分量,从而使分谐波或次谐波靠近共振频率,提供声空化效应.

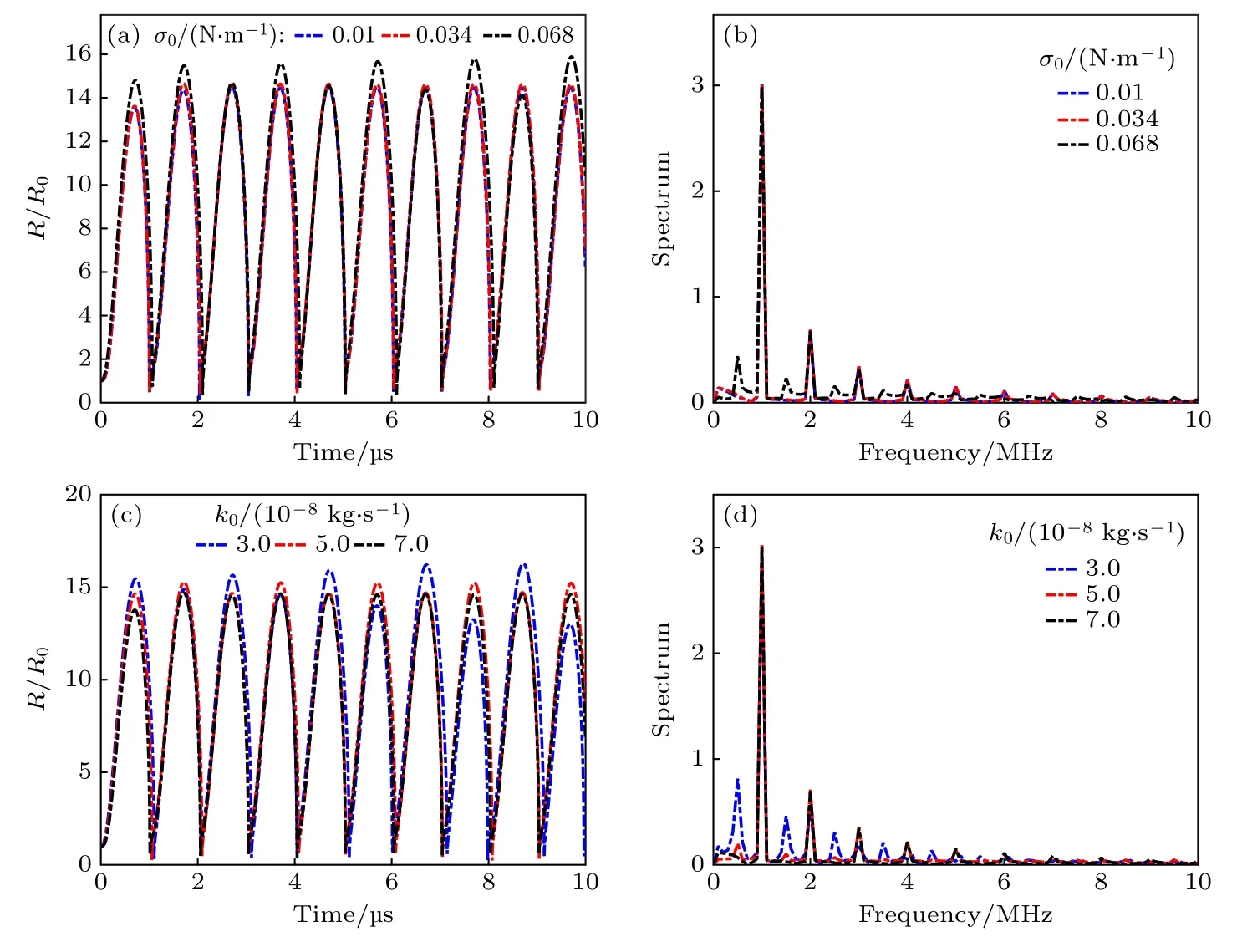
图3 不同包膜材料对微泡动力学行为和频率响应影响 (a),(b) 包膜微泡的初始表面张力;(c),(d) 包膜的黏性参数Fig.3.Effects of different coating materials on bubble dynamic behavior and frequency response of encapsulated microbubbles:(a),(b) Initial surface tension of encapsulated microbubbles;(c),(d) viscosity parameters of encapsulated microbubbles.

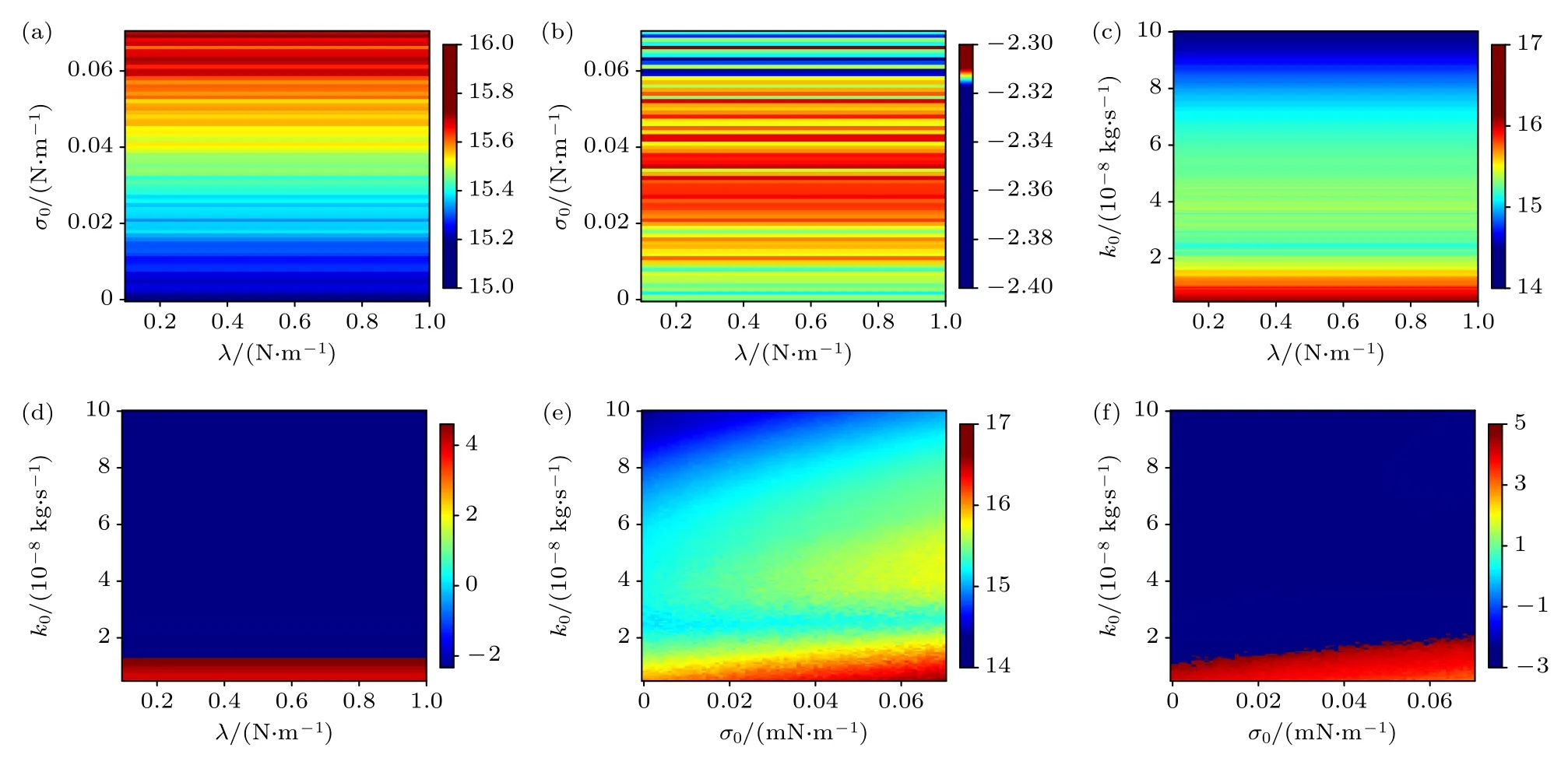
图4 不同包膜材料组合对微泡动力学行为和频率响应影响 (a),(c),(e) 颜色表示微泡半径变化;(b),(d),(f) 颜色表示C 的变化Fig.4.Effects of bubble shell on bubble dynamics and frequency response in the nonlinear ultrasound field: (a),(c),(e) Color bar of is the change of radius;(b),(d),(f) color bar is the change of C.

3.3 声场测量结果与KZK 方程仿真对比

声场实际测量的步骤为: 首先,信号发生器的输入信号通过功率放大器进行放大并发送到匹配单元和聚焦换能器;然后,采用三轴定位系统将水听器对准聚焦换能器的焦点位置,最后进行声场测量.为了防止水中的气泡发生空化,产生谐波,影响数值仿真,聚焦换能器和水听器都在除气水中进行测量.图5(a)对比了真实的聚焦换能器在焦点处的超声波形和KZK 方程仿真出的焦点处超声波形,仿真参数如下:f=1 MHz,P=2.0 MPa,R0=1 μm.图5(b),(c)是实际测量的声场和KZK 方程仿真声场下的微泡径向运动对比,可以发现差距不大,但仿真下的气泡壁运动速度与实际相差0.5 MHz.图5(d)是微泡动力学行为的脉冲响应,可以发现真实的声场在0.1 MHz 的频谱响应较大,而在主频1 MHz 的响应低于KZK 方程仿真的声场.这可能是由于信号发生器发射的是脉冲类型,并且电压在起始位置会发生损耗,导致声压的波形不一致,使得整个脉冲持续时间被当成是一个波形,导致0.1 MHz 的频谱响应较大.

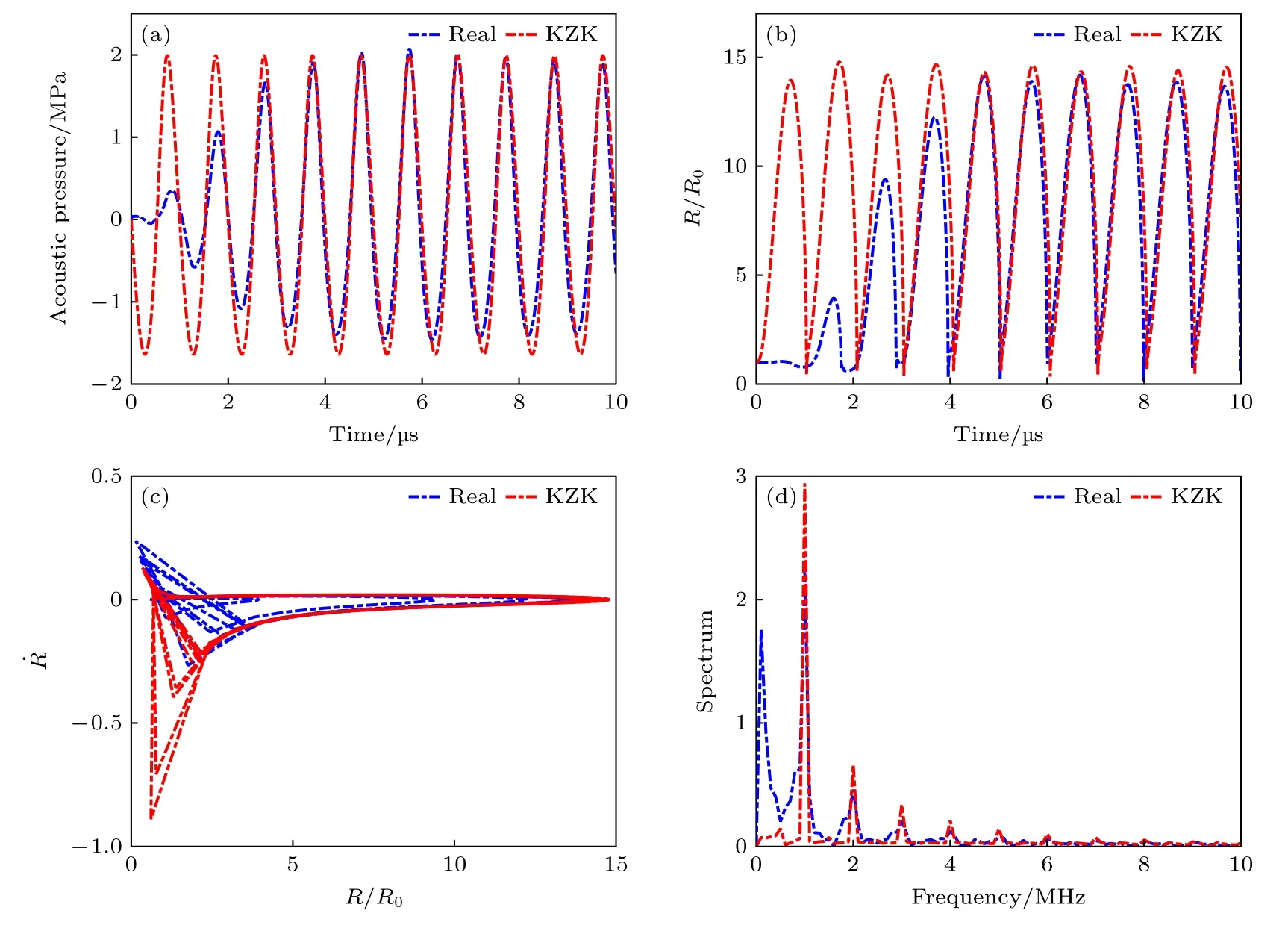
图5 实际测量值与KZK 仿真对比图 (a) 相同正压下实际测量与KZK 方程仿真波形图;(b),(c) 微泡动力学行为的对比;(d) 微泡半径变化的振荡频率响应Fig.5.Actual measured values are compared with the KZK simulation: (a) Actual measurement and KZK equation simulation waveform diagram under the same positive pressure;(b),(c) comparison of the dynamic behavior of microbubbles;(d) oscillation frequency response of the microbubble radius change.

4 总结

微泡动力学分析是聚焦超声应用于声空化、开放血脑屏障、消融以及声致发光中的重要理论基础.考虑在高强度聚焦超声治疗中使用聚焦超声换能器发射的超声由于能量较高会在介质中传播时产生非线性畸变,本文主要采用KZK 方程进行高强度聚焦声场仿真,耦合Gilmore-Akulichev-Zener与包膜的黏弹性模型.相比之前的研究,我们在考虑超声波传播非线性效应的同时加入了脂质微泡模型,可以进行非线性声场的脂质微泡的微泡动力学仿真和微泡振荡频率响应,使微泡动力学仿真和频率响应下的环境更加趋近于真实声场.研究结果表明: 当包膜材料不变时,超声波传播时的非线性会导致微泡的扩张减弱,但会产生更多的谐波分量,包膜微泡的振荡频率分量中谐波含量增大.当超声声压增大时,微泡的径向运动增强,各频率的分量也增高;当超声频率靠近振荡频率时,微泡的径向运动增强,频率分量中主频的峰值增高.

当改变包膜材料时,包膜微泡的初始黏性越小,振荡频率中分谐波的分量越大,包膜微泡的初始表面张力越大,振荡频率中出现的谐波分量越多,分谐波的分量越多.通过调节不同的包膜参数材料组合,可以发现包膜微泡的径向运动行为与振荡频率的改变比较一致,当谐波靠近共振频率时,微泡的声空化效应得以增强;振荡主频分量越高,微泡的声空化效应也会相应增强.本研究进一步为非线性超声消融奠定了理论基础.由于本文以单个微泡作为对象,且未将微泡内部与外部的热传递和热效应考虑进去,后续将重点考虑多微泡的径向运动和平移运动,并结合微泡内部与外部的热效应,进一步分析多微泡在非线性声场激励下的微泡动力学行为和热能传递.