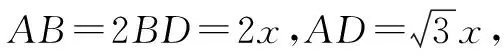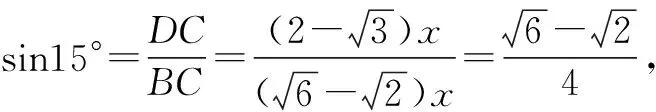构造图形,以形解数
⦿ 江苏省南京市溧水区明觉初级中学 汤爱花
用构造法解题是一种间接、简捷的解题思路,它不是直接去解决某个问题A,而是构造一个与问题A有关的辅助问题B,通过对问题B的解决来实现问题A的解决,而问题B的解决显然更简便、直观.
在初中数学解题中,数形结合思想有着广泛的应用,其中通过构造几何图形来解决代数问题就是数形结合思想中“以形解数”的一种常见的方法与技巧[1].当问题条件中的数量关系具有明显的几何意义,或能以某种方式与几何图形建立起联系时,可以考虑通过构造图形将题设条件与结论在图形中反应出来,然后,借助图形的性质,解决待求或待证明的问题.
借助几何图形的直观性既能够看出“数”之间的某种关系[2],例如统计图表,同时也有望从“形”中获得灵感,得到启发,找到解决问题的方法,例如在列方程解应用题时画的分析示意图等.
1 典例解析,方法对比
已知正数a,b,c,x,y,z,满足a+x=b+y=c+z=k,求证:ay+bz+cx 证法1:因为a,b,c,x,y,z为正数,且a+x=b+y=c+z=k,所以k3=(a+x)(b+y)(c+z)=ay(c+z)+bz(a+x)+cx(b+y)+abc+xyz=(ay+bz+cx)k+abc+xyz>(ay+bz+cx)k. 又k>0,所以k2>ay+bz+cx. 思路与总结:通过观察已知条件式中的a与x,b与y,c与z的平列关系及求证式中左边的轮换对称形式,启发我们,可尝试从k3=(a+x)(b+y)(c+z)入手,经过恒等变形和适当缩放,即可得到欲证的不等式. 证法1是站在代数的角度思考,采用综合法来证明.但是这种方法的缺陷也较明显,主要表现在思路不易畅通,较难看出或建立已知与未知的联系,如果缺乏敏锐的观察能力和较强的恒等变形能力,以及缺乏适当去掉一些正项的技巧,就很难实现从未知向已知的转化. 证法2:如图1,作边长为k的正三角形ABC,在其三边上分别取点P,Q,R,使AP=a,BR=b,CQ=c,则CP=x,AR=y,BQ=z. 图1 整理,得ay+bz+cx 思路与总结:证法2是从a+x=b+y=c+z=k>0,联想到以k为边长的等边三角形.这种证法思路开阔,摆脱了仅对“数”与“式”进行变形的束缚,在全面深入观察、合理联想的基础上,构造了边长为a+x,b+y,c+z(都等于k)的等边三角形,又从结论联想到面积公式,得到了一种新颖的证明方法.与证法1相比较,证法2显然更简捷. 例题求15°的三角函数值. 解法1:如图2,作Rt△ABC,∠C=90°,∠BAC=30°,延长CA到点D,使AD=AB,连接BD. 图2 图3 ① 解法3:如图4,在Rt△ABC中,因为∠BAC=∠B=45°,所以BC=AC. 图4 作∠DAC=30°,∠BAD=15°. 过点D作DE⊥AB于点E,则∠BDE=45°,BE=ED. 解法4:如图5,在△ABC中,AB=AC,∠A=30°,所以∠ABC=∠C=75°. 图5 过点B作BD⊥AC于点D,所以∠ABD=60°. 图6 思路与总结:由于15°是一个特殊的角,它等于30°的一半,因此要求它的三角函数值,除了“利用凑角或拆角、利用三角函数的诱导公式”等代数方法外,还可以考虑构造一个含有15°的直角三角形,然后再利用三角函数的定义及直角三角形的边角关系来求解.其中解法1就是利用三角形的外角作Rt△ABC,使∠BAC=30°,且使∠BAC是等腰三角形的外角,求出各边,再利用三角函数的定义求解;解法2是利用30°角的角平分线得15°角,再由角平分线性质求边的关系,进而求解;解法3是利用45°与30°的差是15°,使问题转化为线段的比而获解;解法4是利用75°与60°的差是15°,通过构造直角三角形来求解;解法5是利用90°与75°的差是15°,通过构造正方形、正三角形、直角三角形等图形来求解.本题旨在考查解直角三角形知识的灵活运用能力,尤其适合训练学生如何根据题意巧妙构造几何图形、寻求一题多解的综合解题能力. 综上所述,构造法是通过对条件和结论的敏锐观察与广泛联想,在已知与未知间架起了一座桥梁,即通过构造一定的数学模型巧妙地完成解题.上述典型例题的解析与一题多解的实战演练,就是灵活运用数形结合思想“以形解数”的精彩呈现,让我们充分感受到了构造图形法解题具有“构思精巧、手法灵活、形象直观、化繁为简、简捷实用”的巨大优越性,值得参考与学习[3].在教学过程中,学生在运用构造图形法解决代数问题时,要在深刻理解题意的基础上,确保构图的准确性与完整性,避免“胡构”“乱造”和“碰运气”,教师要引导学生从不同的角度去分析、思考、比较,形成多样化的解题方法,最终才能达到事半功倍的解题效果.
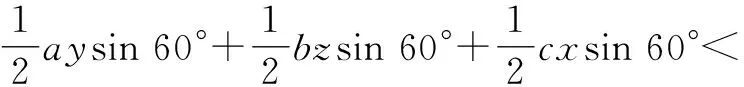
2 变式演练,一题多解