考虑各向异性蠕变的锆包壳鼓胀行为数值模拟方法研究

李 伟,李小雨,段倩妮,王皓坤,武俊梅,刘仕超

(1.西安交通大学 复杂服役环境重大装备结构强度与寿命全国重点实验室,陕西 西安 710049;2.中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610213)

在反应堆运行瞬态或事故工况的高温环境中,Zr合金包壳的强度急剧降低,蠕变速率加快,在裂变气体造成的管内、外压差作用下将出现鼓胀和爆破失效。包壳鼓胀和爆破对反应堆安全带来一系列不利影响,特别是对于高燃耗燃料,包壳鼓胀使燃料芯块失去径向约束,燃料碎块容易重定位至鼓胀区域而使包壳局部热集中,鼓胀区域因此被加速氧化。国内和国际上针对轻水堆燃料包壳的失水事故(LOCA)行为开展了大量实验研究[1-5]。考虑到包壳鼓胀和爆破失效行为的复杂性,通过发展先进、可靠的计算工具进行预测分析有助于加强对该科学问题的认识,理解包壳性能对堆芯安全的影响,有利于开展事故的最佳估算分析。美国从2008年开始开发了有限元燃料性能分析程序BISON,可用于LOCA下的燃料元件行为分析[6],具备二维轴对称和三维建模能力。但是,BISON未考虑α相各向异性蠕变。韩国原子能研究院(KAERI)研究人员采用简化的轴对称解析解对包壳的LOCA高温热-力学行为进行了分析[7-8],表明由于α相的各向异性蠕变行为,轴向单轴拉伸条件下获得的蠕变模型与有限元方法中采用的等效应力蠕变模型存在较大差别。

针对α相区间的Zr包壳各向异性蠕变问题,本文基于Hill准则推导得到应力更新算法和一致切线刚度更新算法。基于有限元软件ABAQUS的材料子程序UMAT,通过加入相转变、各向异性的高温蠕变和失效限值经验模型,初步获得精细化的鼓胀行为分析工具,通过解析解和PUZRY系列爆破实验对该分析工具的合理性和可靠性进行了确认和验证,可为后续高燃耗燃料元件及耐事故燃料包壳(如涂层Zr和FeCrAl包壳)的事故失效行为研究提供参考。

1 材料模型

本研究采用的Zr-4合金导热系数、比热容、杨氏模量、泊松比、热膨胀系数等基本热-力学物性模型均取自MATPRO手册[9]。相变模型来自文献[10],该模型描述了在恒定加热或冷却速率下β相的体积份额。此外,本文采用两种经验模型来判断是否达到爆破,即:FRAPTRAN程序应变限值[11]和Rosinger应力限值[12]。在计算过程中,当包壳管中的等效蠕变应变或环向真应力达到任何一个限值时认为包壳管发生爆破并终止计算。Rosinger爆破应力模型包括3个,分别为上限、平均和下限爆破应力模型。

表1 公开文献中的高温蠕变模型

表1中的蠕变速率参数A、n、Q与β相的体积份额有关。已知纯α相、50% α相和50% β混合相以及纯β相的蠕变速率参数,本文采用传统的加权混合计算方法[4],依据β相的体积份额对表1中的参数Q和n进行线性插值,对系数A的自然对数lnA进行线性差值,计算得到对应的蠕变速率参数。

2 蠕变隐式积分算法

尽管Zr包壳的弹性变形也是各向异性[15],但各向异性程度较小。为简化计算,本文假设Zr包壳的弹性力学性质为各向同性,因此只需两个独立的弹性常数,如通常采用杨氏模量和泊松比。对于Zr-4合金,本文采用MATPRO手册[9]中的杨氏模量和泊松比模型:

(1)

K1=(6.61×105+5.912×102T)·

(ηZr-1.2×10-3)

(2)

K2=-2.6×104CWZr

(3)

(4)

νZr=0.330 3+8.375×10-5(T-273.15)

(5)

式中:EZr为杨氏模型,MPa;T为温度,K;CWZr为冷加工量;ηZr为含氧量,用质量分数表示;Φ为中子注量,m-2;νZr为泊松比。

本文采用Hill准则[16]描述α相Zr合金的高温蠕变变形为各向异性。定义一个屈服函数φ为:

(6)

式中:σ为柯西应力张量,为了方便数值算法的编程实现,本文采用列阵形式,对于三维单元,σ=[σ11,σ22,σ33,σ12,σ13,σ23]T;P为对称矩阵,对于三维几何,其形式为:

(7)

式中,F、G、H、L、M、N为材料的各向异性常数,针对特定材料,需通过实验加以确定。

Hill等效应力与屈服函数的关联如下:

(8)

可以看出,当各向异性常数设置为F=G=H=0.5时,式(8)即为Von Mises应力。根据相关联流动法则,蠕变应变分量与等效蠕变应变的关系为:

(9)

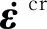
基于有限元方法的蠕变隐式积分算法包含两个步骤:局部迭代和一致切线刚度。局部迭代用于实现应力的更新,需满足的等式如下:

(10)

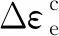
(11)

为了进一步展开式(11),将时间步末的应力张量写为:

(12)

其中:

(13)

(14)

(15)

σtr=σt+DeΔε

(16)

式中:I为单位矩阵;De为弹性矩阵;Δε为总应变张量的增量;Δεcr为蠕变应变张量的增量;σtr为试应力张量;σt为上个时间步末的应力张量,其余变量为运算所需的中间变量。

结合式(6)可求得应变张量对等效蠕变应变增量的偏导数为:

(17)

当各向异性常数为F=G=H=0.5、L=M=N=1.5时,可以证明式(17)等于-3μ,其中μ为剪切模量,这与各向同性Von Mises的情况相符。当上述局部迭代达到收敛后,根据式(13),应力也得以更新。

对于一致切线刚度矩阵,其定义为:

(18)

式中:J为一致切线刚度矩阵;Δσ为应力张量的增量。

对式(13)两边求偏导,并考虑式(9)得到:

(19)

(20)

经过进一步整理,可得到一致切线刚度矩阵为:

(21)

其中:

(22)

(23)

(24)

3 方法验证

3.1 厚壁圆管蠕变解析解

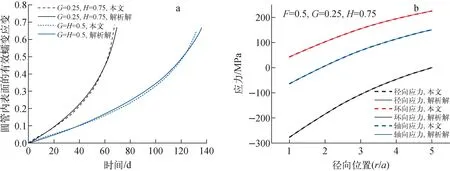
a——圆管内表面等效蠕变应变随时间的变化;b——圆管径向上的应力分布,圆管内表面等效蠕变应变为0.66

3.2 PUZRY实验

采用PUZRY系列鼓胀爆破实验[18]进行验证。包壳管长50 mm,两端各有长5 mm的端塞区,内径9.3 mm,外径10.75 mm。材料为未辐照、未氧化的Zr-4。PUZRY实验在氦气氛围中进行,包含31个工况,温度范围为698～1 201 ℃,涵盖了α相、α+β混合相和β相。本文模拟了其中的28个工况,未模拟爆破时间超过4 000 s的工况。为减少计算时间,利用了轴对称几何。对于α相,各向异性常数取F=0.95、G=0.304、H=0.24、L=M=N=1.5[19]。仅对α相区间的蠕变施加各向异性蠕变算法,对于α+β混合相和β相,认为其为各向同性蠕变。

图2示出PUZRY实验数据与FRAPTRAN爆破应变模型和Rosinger爆破应力模型的对比,其中爆破应力实验数据根据内压和环向应变实验数据计算所得[20]。由图2可见:FRAPTRAN爆破应变模型在α+β混合相和β相区间与实验数据的对比结果不佳,而在α相区间两者的符合程度稍好;Rosinger平均爆破应力模型与α+β混合相区间的实验数据符合较好;Rosinger下限爆破应力模型与β相区间的实验数据符合较好。因此,本文在这3个区域分别采用了FRAPTRAN爆破应变模型、Rosinger平均爆破应力模型和Rosinger下限爆破应力模型来判断实验样品是否发生了爆破。

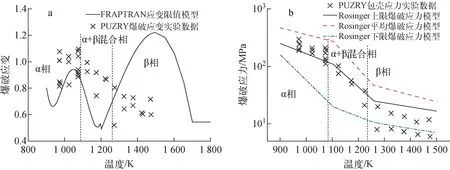
a——爆破应变模型;b——爆破应力模型

计算得到的爆破时间与实验数据的对比如图3所示。除了工况6和19,程序预测的爆破时间与实验数据均符合较好。这两个工况的温度分别为约950 ℃和900 ℃,位于α+β混合相区间,表明本文根据文献中的简单加权混合方法计算该区间的蠕变应变率存在较大偏差,而应开发更为机理性的模型。由图3可见,相对于各向同性蠕变算法,各向异性蠕变算法能明显提高对α相区间蠕变速率预测的准确度,这是因为蠕变速率模型通常基于单轴应力实验数据获得,在将单轴应力用等效应力代替时,各向异性情况下的蠕变速率模型需要根据各向异性常数进行调整,从而改变了蠕变速率。此外,各向异性情况下,等效应力也与各向同性情况下采用的Von Mises应力值不同。图4示出不同温度下计算得到爆破时间与实验数据的对比,直观显示了该算法对α相区间各向异性蠕变速率的适用性。图4结果还表明:对于PUZRY实验条件,Rosinger蠕变模型对于β相区间的适用性较好。

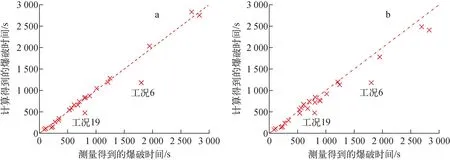
a——各向异性蠕变算法;b——各向同性蠕变算法

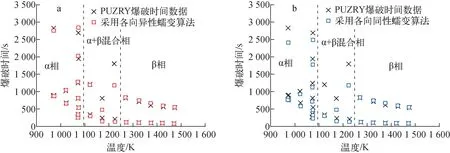
a——各向异性蠕变算法;b——各向同性蠕变算法

爆破时外表面环向应变与实验数据的对比如图5所示。本文未采用单一的爆破准则,而是针对不同的相区间采用不同的爆破准则,使得计算结果在总体上与实验数据符合较好。但在β相区间,对于加压速率大的工况(7.1×10-3MPa/s),程序预测的爆破环向应变较为明显低于实验数据,对于加压速率小的工况(6.4×10-4MPa/s),计算值与实验数据符合较好。这可能是由于当加压速率较大时,塑性变形的作用不可忽视,但现阶段仅考虑了蠕变,导致应力的预测值过大而过早爆破。

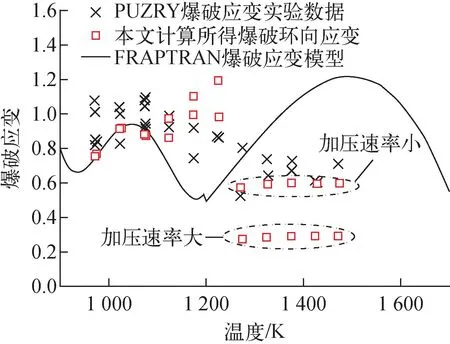
图5 爆破应变计算值与实验数据对比

图6示出包壳轴向变形(实验后的包壳长度/包壳初始长度)与实验数据对比。由于包壳鼓胀造成的环向伸长,在总体积保持不变的情况下,轴向将发生一定程度的收缩。在α+β混合相区间和β相区间,程序预测的轴向变形与实验数据符合较好(注意在这两个相区间均为各向同性蠕变),而在α相区间,包壳鼓胀最为明显,但采用各向同性蠕变算法预测的轴向收缩量明显偏低。在各向同性和各向异性蠕变在α相区间的爆破环向应变相同(均采用了FRAPTRAN爆破应变准则)、而轴向变形差异明显的情况下,表明采用各向同性蠕变算法计算α相的蠕变时,包壳厚度必然比采用各向异性蠕变算法时小,这与数值模拟结果相符。

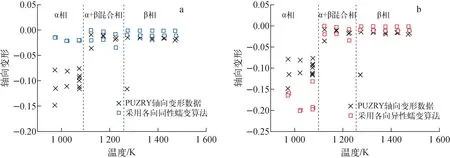
a——各向同性蠕变算法;b——各向异性蠕变算法

图7示出包壳轴向中间位置处的环向应变随时间的典型变化。图7中,PUZRY后的编号表示PUZRY实验的工况号,例如PUZRY-26表示第26实验工况。由图7可见,对于α相区间,各向异性蠕变算法比各向同性蠕变算法预测的包壳环向应变变化更慢,在这种情况下,预测的准确度更依赖于可靠的爆破模型。但对于α+β混合相区间,蠕变模型本身带来的蠕变速率过大,造成计算值与实验数据差异明显,因此有必要开发更机理性的蠕变模型。对于β相区间,预测结果的不确定性似乎还与压力加速率大小有关。图8示出工况PUZRY-30(α相区间)的计算结果及与实验[21]的对比。由图8可见,各向异性蠕变算法预测的包壳发生鼓胀的轴向区间比各向同性蠕变算法更大(即后者预测的鼓胀更为集中在包壳的中间位置),各向异性蠕变算法预测的鼓胀平均环向应变比各向同性蠕变算法预测的值更大。

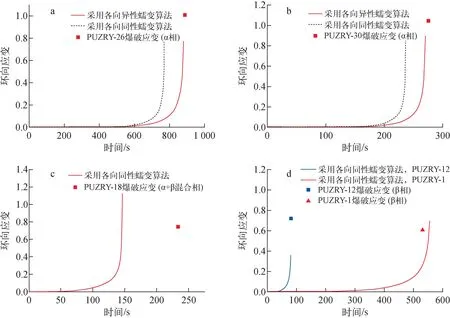
a——PUZRY-26;b——PUZRY-30;c——PUZRY-18;d——PUZRY-12,PUZRY-1

a——各向同性蠕变算法;b——各向异性蠕变算法

4 结论

在高温环境和内外压差条件下,Zr包壳不可避免的存在鼓胀爆破失效。对此现象进行高保真数值模拟研究在高燃耗背景下显得越来越重要,因为包壳的鼓胀爆破失效与高燃耗下的反应堆安全密切相关。本文发展了α相Zr包壳的各向异性蠕变的隐式数值积分算法,且在有限元方法中加以实现,通过厚壁圆管蠕变问题的理论解析解进行了正确性确认,结合FRAPTRAN爆破应变限值模型和Rosinger爆破应力限值模型,模拟了PUZRY鼓胀爆破实验,开展了模型和算法的合理性验证。结果表明:使用各向异性蠕变算法比各向同性蠕变算法能更好地预测α相区间的鼓胀;对于α+β混合相区间,目前常用的加权混合方法计算蠕变速率还存在较大误差;对于β相区间,目前仅考虑了蠕变,因此对加压速率较低的情况适用性较好,但当加压速率更高时,未包含塑性应变可能导致应力预测值偏大而过早地判断发生爆破。此外,与温度等相关的各向异性常数、包含塑性损伤等将在后续的工作中加以考虑。