COSINE多相场子通道程序格架模型开发与评估

陈 林,张 昊,段秉祺,马齐超,周帆帆,杨燕华,赵 萌

(上海交通大学 核科学与工程学院,上海 200240)

定位格架作为反应堆燃料组件的支撑部件,其几何形状会极大的影响燃料组件的热工水力学性能。在反应堆运行期间,定位格架不仅用于固定和夹持燃料棒束,其搅混翼还会对流经燃料组件的冷却剂起到扰动作用,改变燃料组件中的冷却剂流动分布和温度分布,并对定位格架下游区域的换热起到明显的增强作用[1],近年来,许多研究人员通过实验测量以及数值模拟的方法,对不同工况下、不同形状格架的换热增强能力进行了深入的研究[2-3],并推出了一系列更为精确、适用性更广的格架传热增强关系式;再淹没阶段中由于壁面温度很高,通道中具有强烈的相间质能传递、液相剧烈蒸发产生的大量蒸汽并夹带着液滴从底部向上运动[4],由于液滴具有较大的面积体积比,当液滴蒸发时,会带走大量热量并加快蒸汽冷却,进而提高包壳表面的冷却速率[5],而当液滴经过定位格架时,液滴与定位格架会发生碰撞及散射,液滴会被打碎并获得更大的相界面面积和更强的传热能力[6]。因此,格架可增强通道中的传热能力,并对流场变化、液滴行为和再淹没过程具有重要影响。

国家电投集团牵头研发的适用于国和一号的核电厂设计与安全分析软件包(COSINE)[7]经过十年的发展,目前已包含热工水力设计与安全分析、堆芯物理设计、燃料设计、严重事故分析等多种功能。当前,软件包中多相场子通道程序[8]已经开发完成并进行了一系列测试及应用,程序可很好地模拟气相、连续液相、液滴相的流场行为及相间相互作用,并具备了一维与二维导热的计算能力。但当前子通道程序对于格架模型的开发和验证工作尚不完善,需进行进一步的测试和评估。

因此,为准确评价定位格架对流场、传热以及液滴行为带来的影响,评估COSINE多相场子通道程序中格架模型的计算能力,本文选取棒束传热实验装置(RBHT)典型再淹没工况进行建模计算,评估格架模型对通道传热增强、液滴行为以及格架温度等参数的计算能力。

1 COSINE多相场子通道程序中的格架模型

COSINE多相场子通道程序中包括了格架压降模型、壁面传热增强模型、相间传热增强模型、来流液滴破裂模型、格架温度模型、格架再湿模型等。

1.1 格架压降模型

由于格架条带以及搅混翼会阻碍流道,因此,格架的存在会导致通道中出现形阻,流体流经面积变化的通道时速度会发生变化,导致压降变化。格架压降模型中建立了格架压降与形阻系数的关系,表征格架带来的压降效果,模型应用于动量守恒方程中。方程如下:

(1)

(2)

其中:αi、ρi、ui分别为各相的相份额、密度以及速度;Δx为控制体长度;Kgrid为格架阻力系数;Remix为混合相雷诺数;Rgrd为格架在流道中的阻塞比例;Fusr为用户自定义的压降损失乘子。式(2)为格架阻力系数计算公式[9],程序中包括公式计算与用户自定义两种计算方法。

1.2 壁面传热增强模型

格架条带会扰动流道边缘流场并破坏流道中的边界层,使边界处流场由层流向湍流发展,这将增强通道表面与流体间的换热能力。在壁面传热增强模型中,如式(3)所示,通过格架换热增强因子修正原始壁面传热系数,表征格架模型对壁面换热的增强效应,模型应用于能量守恒方程。

htc=htc0·(1.0+Fgrid)

(3)

(4)

其中:htc0为不含格架时壁面传热系数;Fgrid为格架换热增强因子;xcvIN为格架到控制体入口的距离;xcvOUT为格架到控制体出口的距离;Dh为通道的水力学直径。式(3)为格架壁面传热增强关系式[10],式(4)为格架换热增强因子公式,公式根据格架与水力学网格的距离来计算格架换热增强因子,水力学网格距离格架下游越远,则格架换热增强效应越弱。

1.3 相间传热增强模型

由于格架往往具有较大的面积体积比,且不具有功率,因此,格架的骤冷前沿推进速度可能会快于燃料包壳,当格架被浸润后,液膜会覆盖格架,相当于水力学控制体在格架上额外增加了一个连续液相的相界面面积,进而导致相间传热能力增强。式(5)～(7)为格架所带来的相间传热能力增强关系式。

(htc·A)grd=F2ph,grdhtcgAgrd,quench

(5)

(6)

Agrd,quench=PgrdLgrd,quench

(7)

其中:F2ph,grd为格架两相增强因子,采用典型PWR格架增强因子值0.222[11];htcg为单相气对流换热系数;Agrd,quench为格架湿区面积;kg为气相导热系数;Reg为气相雷诺数;Prg为气相普朗特数;Pgrd为格架湿周;Lgrd,quench为格架骤冷高度。式(5)为格架相间传热增强关系式,式(6)为单相气对流换热系数关系式[12],式(7)为格架湿区面积关系式。

1.4 液滴破裂模型

来流液滴碰撞格架时,液滴在格架处发生破裂及散射,形成直径更小的液滴,而大液滴破裂成小液滴后,液滴总表面积的增加,增强了液滴与过热蒸汽间的换热能力,进而加速蒸汽冷却。程序中假设液滴为圆球型,液滴面积与液滴直径呈反比,如式(8)所示。

Adrp=6αd/Ddrp

(8)

Dbrk=DdrpRatiodrp

(9)

(10)

(11)

其中:Ddrp为破裂前的液滴直径;Dbrk为破裂后的液滴直径;Ratiodrp为液滴直径的破裂比例;Rgrd为格架在流道中的阻塞比例;Wed为液滴韦伯数。式(9)为液滴直径破裂公式,将式(9)代入式(8),即可得到破裂前后液滴面积的变化。式(10)、(11)分别为Paik等[13]与Cheung等[5]提出的液滴破裂比关系式,用户可自由选取适当的模型进行计算。

1.5 格架温度模型

格架作为不具备热源的固体构件,其与热构件壁面、气相、液滴相均发生传热,并导致格架温度发生变化,而格架温度变化会进一步影响格架的骤冷前沿高度;在程序中,将格架骤冷前沿高度以下区域划分为格架湿区,湿区温度假设与流体的饱和温度相同,骤冷前沿高度以上区域为干区,式(12)为格架干区温度的变化公式[14]。程序中计算格架温度时,会根据湿区与干区长度比例进行插值计算,确定最终的格架温度。

(12)

(13)

1.6 格架再湿模型

格架作为固体构件,由于其不具备内热源,因此可能会先于燃料棒包壳表面被浸润,而格架的骤冷前沿高度,会进一步影响格架对传热的增强能力,因此,程序中需要对格架的骤冷前沿高度进行计算。式(14)为格架骤冷前沿长度的计算公式[16],式(15)为骤冷前沿速度公式,由式中可知,骤冷前沿推进速度与格架湿区传热系数呈正相关,而与格架温度呈负相关。

(14)

ugrd,quench=

(15)

(16)

2 RBHT再淹没实验建模

RBHT实验装置[17]位于美国宾夕法尼亚州立大学,该装置始建于1997年,并于2002年获得了首次实验结果。近年来,随着先进测量仪器的应用及测量技术的进步,研究人员利用RBHT装置进行了更加精确的再淹没实验,并获得了更为全面准确的瞬态热工水力数据,其中包括液滴的尺寸及速度、蒸汽以及格架温度等。当前,RBHT实验装置所取得的实验数据已被广泛应用在程序开发与评估中,包括APROS、ATHLET、CATHARE、CTF、MARS、RELAP5、TRACE以及SPACE等。

RBHT装置试验段横截面如图1所示,RBHT装置的承压壳为边长为90.2 mm的正方形结构,壁厚为6.4 mm,试验段中包含7×7正方形棒束,其中45根棒为电加热棒,4根棒为非加热支撑棒,棒束中单棒直径为9.5 mm,棒间距为12.6 mm,加热段长度为3.66 m。加热棒轴向功率为非均匀分布,峰值功率因子为1.5,燃料棒轴向功率分布如图2所示。试验段沿轴向布置了7个定位格架,如图3所示,格架底部高度分别为0.10、0.70、1.20、1.74、2.26、2.78、3.30 m。

图1 RBHT装置试验段横截面

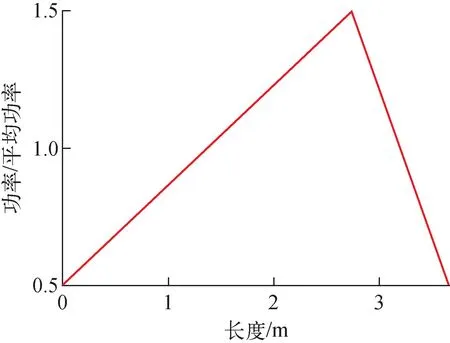
图2 轴向功率分布曲线

图3 RBHT装置试验段中的格架

在RBHT装置建模中,由于本文主要关注格架模型对传热以及液滴参数的影响,因此将RBHT试验段简化为单通道进行建模分析,如图3所示,将加热段均分为30个轴向节点,过冷液体由下方流量入口进入通道中,通道中设置有加热棒,并根据实验参数在相应高度设置7个定位格架,计算时间为1 000 s,计算中最大时间步长设置为10-3s,最小时间步长为10-6s。选取RBHT装置典型试验工况1383[17]与7151[18]进行验证,实验参数列于表1。通过对比格架模型的开启前后壁面温度、骤冷前沿高度、蒸汽温度、格架温度以及液滴参数等,评估COSINE多相场子通道程序中格架模型的计算能力和有效性。

表1 RBHT装置测试算例实验参数

3 计算结果分析与评估

3.1 壁面温度及骤冷前沿变化

图4为带有格架模型与不带有格架模型时,工况1383在2.37、2.54、2.93和3.07 m处包壳温度变化情况,可明显看出,带有格架模型的算例中,各监测点处的包壳冷却时间明显更早,且带有格架模型的包壳温度变化情况与实验结果符合更好。此外,由图4c、d可知,对于通道上方的监测点,带有格架模型的算例计算的包壳峰值温度(PCT)更低,在2.92 m与3.07 m监测点处,带有格架模型的计算中PCT分别降低了29 K与41 K。如图5所示,与关闭格架模型相比,开启格架模型时PCT的计算误差由10%降至7%。图6对比了骤冷前沿位置的计算值与实验值,可发现,带有格架模型时计算的骤冷前沿位置与实验符合较好,而不带有格架模型的算例中,计算的骤冷前沿速度明显低于实验值,这是由于格架模型具有增强壁面传热与相间传热的效应,因此有效地增强再淹没工况下的换热能力。图7对比了关闭格架壁面传热增强模型与相间传热增强模型时的计算效果,可发现,关闭相间传热增强模型后,骤冷前沿速度低于开启全部格架模型时的计算结果,且当节点高度大于1.7 m时更为明显,这表明关闭相间传热增强模型后,通道上部包壳的冷却速度明显减慢,此外,关闭相间传热增强模型后,在计算结束时,通道的骤冷前沿高度为3.1 m,通道未能完全浸润;观察关闭壁面传热增强模型时的计算结果,可发现,此时程序计算的骤冷前沿推进速度与关闭全部格架模型时十分类似,远低于仅关闭相间传热增强模型时的骤冷前沿推进速度,计算结束时,格架的浸润高度仅有2.75 m,甚至低于关闭全部格架模型时的浸润高度2.87 m,这是由于当关闭格架壁面传热增强模型时,格架的压降模型等仍在发挥作用,此时格架的阻力作用会使蒸汽流速降低,进而导致夹带至通道上部的液滴质量减少,影响过热蒸汽与液滴间的换热,从而加剧了传热恶化。因此,格架壁面传热增强模型对于加速骤冷前沿推进速度、增强壁面传热的效果更为显著。综上,格架模型可有效地提高计算的骤冷前沿速度,加速包壳冷却,并降低计算的PCT。

图4 包壳温度变化

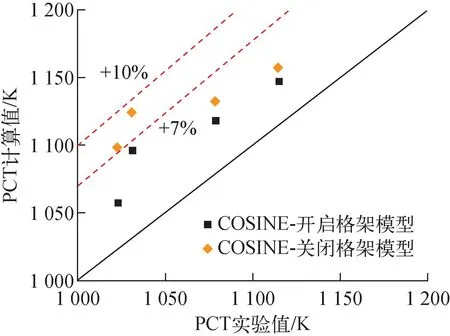
图5 PCT计算误差

图6 骤冷前沿位置

图7 骤冷前沿位置计算对比

3.2 蒸汽温度变化

图8a、b展示了带有格架模型与不带有格架模型时1383工况在2.54 m与3.07 m处蒸汽温度变化情况。可发现,在计算前期(<300 s),格架模型对蒸汽温度的影响较小,格架模型开启与关闭时,计算的蒸汽温度变化非常类似,这是由于此时监测点远离再淹没水位位置,蒸汽夹带而来的来流液滴较少,此时格架对液滴的打碎效应和换热增强效应并不明显;在再淹没工况的后期(>500 s),带有格架模型的算例计算的蒸汽冷却速率更快,与实验结果符合更好,这是由于此时监测点与再淹没水位较近,大量液滴被气相夹带撞击格架被打碎,气相与液滴间的相间传热面积增大,蒸汽相的相间换热能力得到增强,因此气相被更快的冷却。图8c表征了液滴破裂模型对2.54 m监测点处蒸汽冷却速率的影响,当关闭液滴破裂模型时,在再淹没工况的后期(>500 s),蒸汽冷却速率明显减缓,蒸汽温度变化趋势与关闭全部格架模型时十分类似,这是由于此时该监测点靠近再淹没水位,大量液滴被气相夹带而来撞击格架并被打碎,极大改善了气相换热,关闭液滴破裂模型将导致气相换热能力大幅下降。因此,对于靠近再淹没液位的该监测点,格架的液滴破裂效应对加速蒸汽冷却具有重要影响。图8d表征了液滴破裂模型对3.07 m监测点处蒸汽冷却速率的影响。可发现,该监测点的液滴破裂效应对蒸汽冷却速率的影响较小,蒸汽温度的变化与开启全部格架模型时十分类似,这是因为该监测点位于通道顶部区域,远离再淹没水位,下方蒸汽夹带到此的液滴量很少,该监测点处蒸汽温度的下降速率主要受格架对壁面及相间传热增强能力的影响。综上,格架模型考虑了格架对液滴的破裂效应及传热增强效应,可更好地预测通道不同高度的蒸汽温度变化情况。

图8 蒸汽温度计算对比

3.3 格架温度变化

图9a、b示出了1383工况下格架5、6的温度变化情况,在计算前期(<200 s),程序计算的格架温度整体较实验中更高,且实验中会出现格架温度迅速下降至液相饱和温度的情况。这是由于实验中,当格架温度探头被液相覆盖时,格架温度会迅速下降至饱和温度,而COSINE程序通过对干湿区温度插值来确定格架温度,因此,计算中不会出现类似实验中格架温度陡降的现象。图9c为7151工况下,格架6的温度变化图。可发现,程序计算的格架温度与实验值符合良好,对照COSINE与COBRA-TF[18]的计算结果可发现,两程序计算的格架温度变化趋势非常相似,但COBRA-TF计算的格架前期温度略低。综上,格架模型可较好地模拟格架温度的变化情况,计算结果合理可靠。

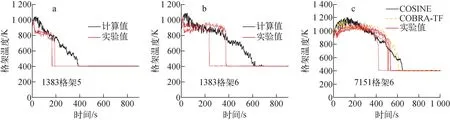
图9 格架温度变化

3.4 液滴尺寸变化

图10a示出了7151工况下Cheung与Paik模型计算的格架6上下游处液滴索特直径(DSMD)的变化情况。可发现,由于格架对液滴的打碎作用,计算的格架6下游的液滴索特直径整体低于上游液滴的索特直径;观察液滴索特直径随时间变化趋势,可发现计算的液滴直径随时间呈现先增大后减小的趋势,液滴直径在约600 s时发生转折,这是由于此时通道中监测点处壁面传热模式由临界后膜态沸腾转换为临界前核态沸腾,通道中换热能力迅速增强,液滴被大量蒸发导致直径减小,同时也导致包壳温度迅速下降。

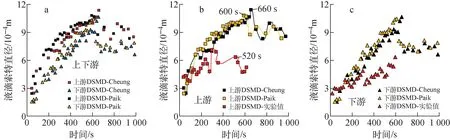
图10 格架6液滴索特直径

图10b、c展示了不同模型下格架6上下游位置液滴索特直径的计算结果与实验结果的对比。可发现,在计算前期(<300 s),程序计算的格架前后液滴索特直径与实验值符合良好,而在计算后期(>400 s),程序计算的格架前后液滴索特直径均明显高于实验值。由图10b可知,程序计算的液滴直径转折点时间分别为600 s(Paik模型)与660 s(Cheung模型),而实验中液滴直径转折点时间约为520 s,由上述分析可知,这是由于格架6上游监测点处计算的骤冷时间较实验值更晚所导致。由图10c可知,程序计算的格架6下游直径变化趋势与实验值符合良好,在实验数据覆盖的时间区间内,液滴索特直径呈现逐步增大的趋势。

计算的格架上下游液滴平均索特直径与实验值的对比结果列于表2。可发现,计算的格架6上下游液滴平均索特直径明显高于实验值,这可能是由于液滴夹带模型不准确所导致,未来需要继续深入研究;观察计算的格架前后液滴散射直径比,可发现,Cheung模型计算的液滴直径散射比为0.81,Paik模型计算的液滴直径散射比为0.83,实验测得液滴直径散射比为0.78,程序不同模型计算的液滴直径散射比均与实验值符合良好,同时Cheung模型的计算结果与实验值符合更好。综上,程序中采用的格架模型可较好地模拟格架处液滴的破碎效应。

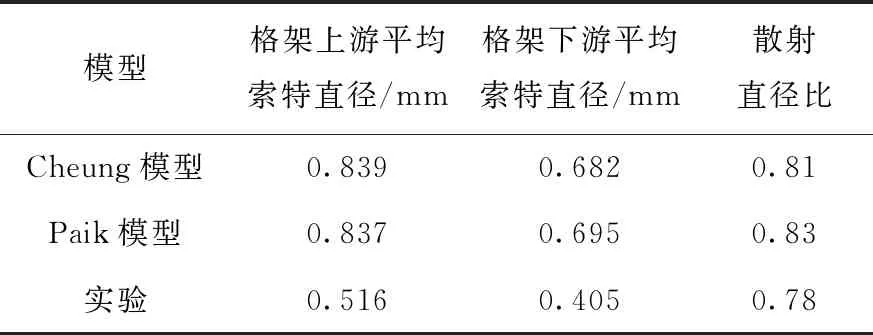
表2 格架6上下游液滴平均索特直径

3.5 液滴速度变化

图11为格架6上游位置的液滴速度变化情况。由实验曲线可发现,随着再淹没的发展液滴的速度逐渐降低,这是由于随着再淹没的发展,骤冷前沿位置逐渐沿通道向上移动,格架6距离再淹没液位距离逐渐减小,导致大量液滴被气相夹带到达格架6上游位置,而由于夹带液滴的增多,液滴质量增加进而导致速度下降。对比计算结果与实验值,可发现,程序计算的液滴速度变化趋势与实验值符合较好,但计算的液滴速度明显较实验值下降更快,这可能是由于程序中所采用的夹带模型的误差所导致,当通道中夹带液滴过多时,较大的重力效应会导致液滴速度迅速下降。此外,格架模型在开启与关闭时,液滴速度的计算结果相差不大,这是由于该监测点位于格架6上游位置,此时格架6还未与液滴接触并影响其运动行为,液滴速度仅受到上游较远处格架5的影响,而此时格架5对当前位置液滴动量的影响已不再显著。综上可知,程序可预测再淹没工况中液滴速度的变化趋势,但计算的液滴速度下降趋势明显快于实验结果,未来需继续优化液滴与格架相关模型以提高程序的预测能力。

图11 格架6上游液滴速度变化

4 结论

本文介绍了自主研发的具有自主知识产权的COSINE多相场子通道分析程序中的格架模型,并选取RBHT典型再淹没实验工况对程序中格架模型的计算能力进行评估。结果表明:采用了格架模型的算例中,计算的包壳骤冷前沿推进速度明显更快,包壳温度与蒸汽温度下降更快,采用格架模型可将程序计算的PCT偏差由10%降至7%;程序中计算的格架温度与实验结果符合良好,计算结果合理可靠;格架模型可很好地预测液滴破碎行为及液滴直径的变化趋势,程序计算的格架直径破碎比与实验值符合良好,但程序计算的平均液滴索特直径明显高于实验值,未来需进行进一步研究;程序可较好地预测再淹没工况下格架附近液滴速度的变化趋势,但计算的液滴下降速度明显快于实验值,未来还需对相关模型继续进行深入研究,提高COSINE多相场子通道程序中格架模型的计算精度。综上,COSINE多相场子通道程序中采用的格架模型是有效且合理可靠的,可显著提高程序对再淹没工况下的各类热工水力学参数的预测能力。